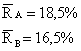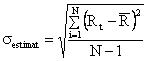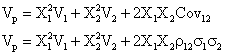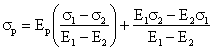Riscul
si rentabilitatea unui portofoliu de titluri
Riscul unui activ se defineste prin
variabilitatea probabila a rentabilitatii viitoare a activului. De exemplu,
daca un investitor cumpara obligatiuni guvernamentale pe termen scurt de 1
milion u.m. cu un randament anticipat 7% atunci rentabilitatea investitiei este
de 7% si poate fi estimata cu precizie, acest tip de investitie fiind fara
risc. Insa daca milionul este investit in actiuni ale unei companii recent
infiintate, avand ca profil de activitate, de exemplu, explorarea petrolului
intr-o zona petroliera, rentabilitatea investitiei nu poate fi estimata precis.
Un analist, studiind rezultatele posibile, ar putea estima o rata de
rentabilitate asteptata, din punct de vedere statistic, de 20%.
Investitorul se poate astepta si la faptul ca rata de rentabilitate reala
poate varia, de exemplu, de la +100% la -100%. Existenta posibilitatii
semnificative, de a obtine o rentabilitate reala mult mai mica decat
rentabilitatea asteptata, face ca actiunile sa fie considerate ca riscante.
Deci, riscul este legat de
probabilitatea de a avea o rentabilitate mai mica decat cea asteptata. Cu cat
este mai mare sansa unei rentabilitati mici sau negative, cu atat mai riscanta
este investitia.
Orice decizie de investitie (orice
decizie de afaceri) necesita o previziune a unor evenimente viitoare. In
deciziile de alocare a capitalului, previziunile cheie sunt legate de fluxurile
de numerar anuale ale proiectului. De regula, aceasta previziune este facuta
sub forma unui numar, adica o estimare punctuala, denumita frecvent estimatia
cea mai probabila (500 u.m. anual timp de 3 ani). Ne punem intrebarea: cat de
buna este aceasta estimatie punctuala? Adica, cata incredere putem avea in
rentabilitatea previzionata: este foarte certa, foarte incerta sau undeva la
mijloc? Acest gen de incertitudine este definit si masurat prin distributia
de probabilitate a predictiei (asocierea estimarii probabilitatii cu
fiecare rezultat posibil).
Masura traditionala a riscului
aplicabila proiectelor individuale este legata de variabilitatea rezultatelor
si este definita prin distributia de probabilitate.
Proiect A
|
Rentabilitate
|
Probabilitate
|
|
|
|
|
|
|
Proiect B
|
Rentabilitate
|
Probabilitate
|
|
|
|
|
|
|
Rata estimata (asteptata) a rentabilitatii se calculeaza
dupa relatia:
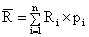
-unde Ri reprezinta ratele de rentabilitate
posibile, iar pi probabilitatile corespunzatoare fiecarei rentabilitati.
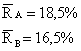
Pentru a fi utila o masura a riscului
trebuie sa aiba definita o valoare. Este necesar sa se masoare largimea
distributiei de probabilitate. O astfel de masura este deviatia standard
(s). Cu cat este mai mica s cu atat este mai stransa distributia de
probabilitate si deci riscul activului respectiv este mai mic.
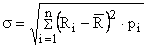
-s este o probabilitate - media ponderata a deviatiei de
la valoarea asteptata si ne arata cu cat este valoarea reala mai mare sau mai
mica decat valoarea asteptata.
Rentabilitatile sunt calculate pe baza fluxurilor de
numerar prevazute in cazul unor scenarii alternative. O anumita rata de
rentabilitate poate fi interpretata ca rata interna de rentabilitate a proiectului
pe baza fluxurilor de numerar asociate (proiectul costa 1000 u.m. si are 3
valori posibile ale fluxului prevazut de numerar).
* 210
u.m./an ..3 ani
* 438
u.m./an . 3 ani
* 711 u.m./an
. 3 ani
Rata interna
a rentabilitatii (R.I.R.)
1000 = CF1/(1 + RIR) + CF2(1 + RIR)2 + CF3/(1 + RIR)3
Daca fluxul de numerar este de 210 u.m. rezulta ca RIR =
-20%.
Pentru
fluxurile anuale de numerar de 436 u.m. sau 711 u.m., RIR este respectiv 15%
sau 50%.
Daca
singurele date disponibile sunt valori ale rentabilitatii intr-o perioada
trecuta deviatia standard a rentabilitatii se estimeaza folosind formula:
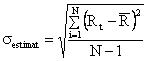
Daca distributia de probabilitate este continua, astfel ca
probabilitatea poate fi estimata pentru fiecare rezultat posibil, atunci putem
trasa o curba continua care uneste toate ratele rentabilitatii. Distributiile
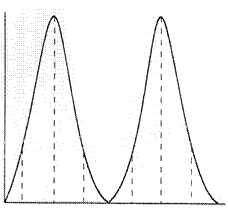
de rentabilitate pentru cele doua proiecte E si F prezentate in fiura 6.1 sunt
exemple de distributii continue de probabilitate. Graficul
proiectului F prezinta doua carcteristici ale unei investitii mai favorabile:
(1) are rentabilitatea asteptata mai mare si (2) distributia de probabilitate
este mai stransa, in consecinta un risc mai mic.
Un investitor are de ales intre doua
titluri T1 si T2 sau are in mod egal posibilitatea constituirii unui portofoliu
P repartizand suma pe care doreste s-o investeasca intre cele doua
titluri.
Anticiparile sale privind
comportamentul titlurilor in perioada viitoare sunt rezumate in varianta
urmatoare:
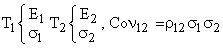
Reamintim semnificatia notatiilor utilizate, i si j
fiind cele doua titluri oarecare:
Ei -
speranta matematica a ratei rentabilitatii titlului i;
si -
abaterea standard a ratei rentabilitatii titlului i;
rij - coeficientul de corelatie intre ratele
rentabilitatii titlurilor i si j;
Covij -
covarianta intre ratele rentabilitatii titlurilor i si j.
Portofoliul P este obtinut combinand
cele doua titluri in proportia X1 si X2.
Totalitatea sumei disponibile este
investita in T1 si T2. Avem relatia:
X1 + X2 = 1cu X1, X2 ³ 0 sau 0 £ X1 £ 1; 0 £ X2 £ 1.
Speranta matematica a ratei
randamentului portofoliului P(Ep):
Ep = X1E1 + X2E2
Speranta randamentului este media
ponderata a sperantei randamentelor titlurilor, ponderea fiind proportiile.
Dispersia ratei randamentului
portofoliului P(Vp):
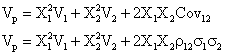
Dispersia portofoliului este functie de
dispersia fiecarui titlu, de proportiile in care sunt combinate si de
covarianta intre cele doua titluri.
Plecand de la doua titluri T1 si T2
astfel incat E1 < E2 si s1 < s2, diferite portofolii care pot fi
constituite vor fi studiate in planul E - s. Vom vedea ca potrivit gradului de
dependenta (sau de covarianta sau de corelatie) intre T1 si T2, diferite
ansamble de portofolii pot fi obtinute. Se disting trei cazuri:
1) Daca r12
= 1: titlurile T1 si T2 sunt perfect si pozitiv corelate ceea ce semnifica
anticiparea pentru randamentul acestor titluri a unor miscari perfect
concordante in timp, dar cu amplitudini diferite (figura 6.3).
In acest caz:
se scrie
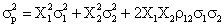 cu
cu 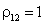 .
.
Adica
Sursa: Modelarea deciziilor economico-financiare
Deviatia procentuala de la medie a
proiectului C este considerabil mai mare decat deviatia de la medie a
proiectului D. Aceasta inseamna ca pentru fiecare u.m. de profit obtinut
proiectul C este mai riscant decat proiectul D.
Sursa: Modelarea deciziilor economico-financiare
Abaterea standard a portofoliului este
media abaterilor standard ale titlurilor care il compun. Reunind cele doua
ecuatii si raportand la randamentul si la riscul portofoliului P, 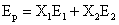 si
si 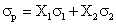 obtinem
ecuatia
obtinem
ecuatia 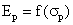 , ca spatiu al
combinarilor titlurilor T1 si T2 in planul E - s. Stim ca X1 + X2 = 1,
adica
, ca spatiu al
combinarilor titlurilor T1 si T2 in planul E - s. Stim ca X1 + X2 = 1,
adica
X2 = 1 - X1.
Din ecuatia 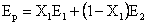 , obtinem
, obtinem 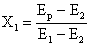 daca E1¹E2 pe
care il inlocuim cu ecuatia lui sp.
daca E1¹E2 pe
care il inlocuim cu ecuatia lui sp.
Obtinem:
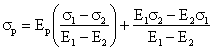
Aici relatia
intre Ep si sp este liniara si se reprezinta grafic printr-o dreapta.
Toate
portofoliile obtinute plecand de la T1 si T2 (cu X1 si X2 ³ 0) se gasesc pe
segmentul de dreapta T1T2.
2) Daca r12
= -1, titlurile T1 si T2 sunt perfect si negativ corelate.
Anticipam
pentru randamentul acestor titluri fluctuatii perfect opuse.
In acest caz
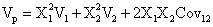
se
scrie:
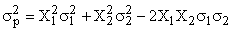
adica:
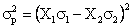
Abaterea
standard fiind totdeauna pozitiva, vom face discutie pentru semnul expresiei (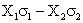 )
care variaza in functie de X1 si X2.
)
care variaza in functie de X1 si X2.
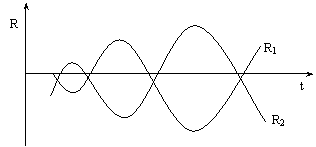
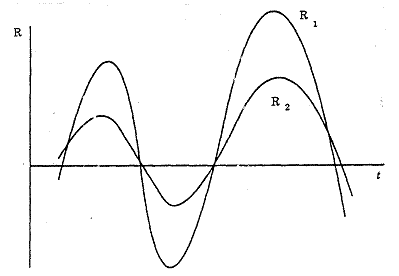
Sursa: Modelarea deciziilor
economico-financiare
Evolutia randamentelor a doua titluri perfect si negativ corelate
Pentru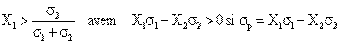
Aceasta
relatie, impreuna cu relatia Ep = X1E1 + X2E2, permite determinarea ecuatiei de
legatura intre Ep si sp.
Obtinem 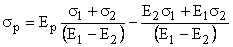 .
.
Este vorba
de o relatie liniara reprezentata grafic de o dreapta. Partea, din aceasta dreapta,
corespunzatoare la:
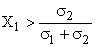
este locul portofoliilor obtinute plecand de la titlurile
T1 si T2 (ramura 1 a graficului 6.6).
Pentru
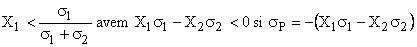
Procedand ca mai sus obtinem ecuatia
liniara legand Ep si sp.
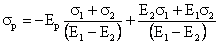
O parte a acestei drepte, cea corespunzatoare lui 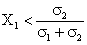
este legea portofoliilor obtinute combinand T1 si T2 (ramura 2 a graficului
8.6).
In sfarsit,
pentru 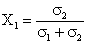 avem sp = 0.
avem sp = 0.
Acest
rezultat este remarcabil, deoarece el arata ca plecand de la doua titluri
riscante este posibil ca alegand riguros proportiile (0 £ X1 si X2 £ 1), sa se
construiasca un portofoliu neriscant. Acest rezultat este posibil daca titlurile T1, T2 sunt
perfect si negativ corelate.
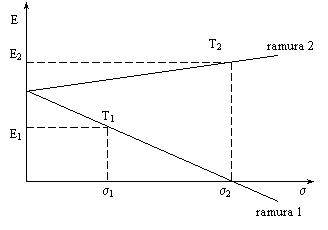
Sursa: Modelarea deciziilor economico-financiare
Legea portofoliilor obtinute plecand de la titluri perfect si negativ
corelate
3) Daca
-1 < r12 < +1 (incluzand r12 = 0) fluctuatii anticipate pentru titlurile
T1 si T2 nu sunt perfect dependente (pozitiv si negativ). Este cazul general,
exista un anumit grad de corelare intre ratele randamentelor titlurilor
datorita faptului ca toate urmaresc mai mult sau mai putin fluctuatiile
generale ale economiei. In urcare in perioada de expansiune,
ratele randamentelor titlurilor cunosc o incetinire si chiar o scadere cand
conjunctura este mai putin favorabila. Pe ansamblu, titlurile sunt pozitiv (dar
nu perfect) corelate intre ele si cu ansamblul economiei. Un titlu corelat
negativ este foarte rar, minele de aur fiind un exemplu din aceasta categorie
de titluri.
In cazul
general, obtinem pentru un portofoliu de doua titluri:
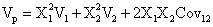
cu -1 < r12 < +1
adica: 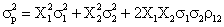 care nu
poate fi pusa sub forma unui patrat perfect, ca in cazul celor doua situatii
precedente.
care nu
poate fi pusa sub forma unui patrat perfect, ca in cazul celor doua situatii
precedente.
Plecand de
la aceasta ecuatie si de la cea a lui Ep (Ep = X1E1 + X2E2), stabilim relatia
care leaga pe Ep si sp.
Din ecuatia
lui Ep obtinem X1 = (Ep-E2/(E1-E2) valoare pe care o introducem in ecuatia lui
Vp. Dezvoltand obtinem:

Ecuatia obtinuta in planul E-V este aceea a unei parabole. In
planul E-s ecuatia
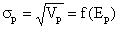
reprezinta o hiperbola din care
retinem o ramura, respectiv aceea corespunzand valorilor sp pozitive.
In figura 6.7 sunt reprezentate curbele
obtinute pentru diferite valori posibile ale coeficientului de corelare al
celor doua titluri. Pe masura ce corelarea intre cele doua titluri scade,
concavitatea curbei se accentueaza. Trecem astfel progresiv de la dreapta T1T2
corespunzand corelatiei maxime (r12 = 1) la curbe la inceput usor rotunjite,
apoi din ce in ce mai accentuate care se ridica deasupra si la stanga dreptei
pe masura ce trecem la grade de corelare mai mici, pana ajungem cu r12 = -1 la
o solutie unde legea portofoliilor este compusa din doua segmente de dreapta
incadrand curbele descrise anterior. Cazul a doua titluri independente
(r12 = 0) constituie o etapa in aceasta evolutie.
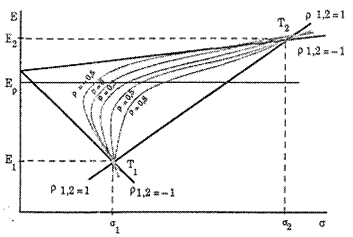
Sursa: Modelarea deciziilor economico-financiare
Figura Locul portofoliilor obtinute plecand de la doua titluri. Ansamblul de
cazuri posibile
Cateva
observatii pot fi formulate despre avantajele diversificarii.
a)Diversificarea
este interesanta imediat ce r12 < 1.
b) Plecand de la doua titluri T1 si
T2 este posibil in anumite cazuri sa se obtina portofolii avand un risc
inferior riscului fiecarui titlu care-l compune; aceasta este posibil cand
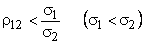
Aceasta va
fi intotdeauna posibil cu titluri cu risc independente sau corelate negativ
(r12 £ 0).
c) Exista in
fiecare situatie un portofoliu de risc minim care corespunde proportiilor X1 si
X2 determinate. Acest portofoliu de risc minim are un risc nul intr-un singur caz,
cand r12 = -1. In toate celelalte cazuri riscul minim este pozitiv.
Nu este deci
posibil sa se elimine riscul, decat in cazul in care combinam doua titluri
perfect si negativ corelate.