Probleme de baza ale teoriei erorilor de masurare
Scopul toriei erorilor de masurare
Daca o marime este
supusa la mai multe observatii, marimile obtinute sunt
diferite chiar daca masuratorile sunt executate in aceleasi
conditii de catre acelasi operator si cu instrumente de mare precizie.
Cauza
acestor nepotriviri de valori se datoreste erorilor care afecteaza intodeauna
o masuratoare, facand ca valoarea adevarata a
marimii masurate sa nu poata fi cunoscuta
niciodata.
Practic,
in conditiile in care valoarea adevarata nu poate fi
obtinuta, se
determina o valoare apropiata intr-un
grad mai mare sau mai mic in functie
de scopul pentru care se executa masuratorile.
Gradul de apropiere a valorii determinate
fata de cea adevarata
caracterizeaza decizia determinarii.
Ca
urmare prelucrarea masuratorilor efectuate asupra unei marimi
urmareste
obtinerea celei mai bune valori a acesteia si a diferentei
maxime intre valoarea determinata si valoarea masurata.
1.2 Importanta
teoriei erorilor de masurare
Baza de date necesara rezolvarii problemelor
geodezice, fotogrametrice si topografice, o constituie informatiile
care provin din observatiile efectuate asupra unor masuratori
si care sunt unghiuri, distante si inaltimi. Calitatea informatiilor
obtinute din masuratori este functie directa de
volumul de observatiilor si precizia oferita de aparatele utilizate in efectuarea lor.
In consecinta se impune ca
pornind de la scopul pentru care sunt efectuate
masuratorile sa se stabileasca valorile
corespunzatoare ca marime si precizie, luand in considerare
aspectul economic referitor la volumul observatiilor necesar si suficient.
Metodele
de prelucrare trebuie sa fie actuale sa rezolve cu succes aceste
cerinte
1.3 Clasificarea erorilor
Erorile care actioneaza si
afecteaza intotdeauna masuratorilor sunt complexe,
iar o analiza a lor impune individualizarea lor dupa anumite
criterii si anume:
Erori
dupa cauzele lor (instrumente personale si de mediu);
Erori
dupa valoarea de referinta( valori
reziduale);
Erori dupa marimea
lor(tolerabile si netolerabile);
Erori dupa modul lor de actionare
(sistematice si accidentale).
1.4 Clasificarea
masuratorilor
Masuratorile ale caror
erori constituie obiectul de studiu al disciplinei difera
dupa modul de prezentare si in raport cu conditiile in care
sunt executate.
Astfel, dupa modul de prezentare,
pot fi:
Masuratori
directe;
Masuratori
indirecte;
Masuratori
directe cu conditii;
Masuratori indirecte
cu observatii multiple;
Masuratori
indirecte supuse la conditii.
Dupa conditiile in care
sunt executate, pot fi:
Masuratori
de aceeasi precizie;
Masuratori
de precizii diferite.
1.5 Repartitia erorilor
accidentale.
Admitem ca asupra unei
marimi au fost efectuate observatii n observatii si
ca eroarea de marime 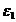 s-a produs de
s-a produs de 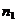 ori.
ori.
Cu
aceste elemente probabilitatea 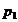 de a se produce eroarea
de a se produce eroarea 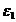 se exprima
se exprima
astfel:
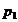


Pentru o eroare  de alta marime si cele n observatii vor exista
de alta marime si cele n observatii vor exista 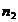 aparitii,
iar probabilitatea
aparitii,
iar probabilitatea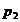 va
fi:
va
fi:
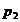
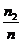
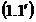
Se constata
ca probabilitatea depinde valoric de marimea erorii, deci este o
functie de aceasta. In consecinta:
 =
=



Formarea
functiei din  exprima legea de distributie
a erorilor cunoscuta sub numele de distributia normala
stabilita de Gauss.
exprima legea de distributie
a erorilor cunoscuta sub numele de distributia normala
stabilita de Gauss.
Pentru
determinarea functiei Gauss a facut ipoteza ca valorile unei
serii de observatii se grupeaza in jurul valorii mediei aritmetice care,
se demonstreaza ca, este cea mai apropiata de valoarea
adevarata de valoarea marimii masurate, sau altfel spus,
cea mai probabila valoare a acestei marimi.
Daca 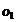 , o
, o
 sunt observatii efectuate direct si
au aceeasi precizie,
sunt observatii efectuate direct si
au aceeasi precizie,
atunci valoarea
probabila M este:
M=
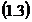
fata de care, erorile
reziduale sau aparente sunt:
v = o
= o - M i=
1,2, . .. .
- M i=
1,2, . .. . 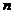

Probabilitatiile prezentei
fiecarei din aceste erori vor fi:
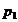


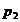
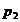



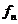
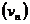
Probabilitatea
P ca toate erorile sa se fi
produs este conform teoriei probabilitatii compuse, produsul
probabilitatilor, respectiv:
f
 f
f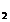
 , . . f
, . . f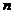
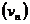 = p
= p , p
, p , . . . . p
, . . . . p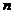 = P
= P 
Pentru
ca erorile v sa fie mici si
deci valoarea lui M sa fie cea mai buna (cea mai apropiata de
valoarea adevarata probabila) se impune
P = maxim
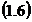
Extremul probabilitatii
P se obtine pentru valorile care
anuleaza derivata ei sau derivata logaritmului in raport cu
derivata V.
Aplicand logaritmi naturali obtinem

 +
+ 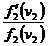 + . . . ..+
+ . . . ..+

Sau:


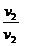
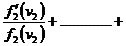
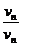
 = 0
= 0 
Avem:
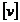 =0
=0

Expresia  exista atunci cand:
exista atunci cand:

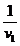
 =
= 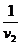
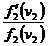 = . . . =
= . . . = 
 = 2
= 2
Respectiv:
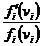 =
=  ;
; 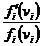
 = k
= k d
d

Integrand avem:

 =
=  d
d
Si

In final avem:

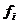
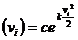

Dar,
probabilitatea de a se produce o eroare 
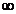 ,
conform egalitatii
,
conform egalitatii  este egala cu
este egala cu 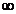 nu zero cum exista in realitate. Ca urmare, in locul lui
nu zero cum exista in realitate. Ca urmare, in locul lui  se introduce
se introduce  si obtinem:
si obtinem:

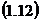
Care reprezinta legea de distributie a erorilor
accidentale.
Deci,functia de probabilitate este
 =
=

Indicele
de precizie al unei masuratori. Ponderea
masuratorii.
Daca
se reprezinta grafic functia  se obtine curba de distributie
cunoscuta si sub numele de clopotul lui Gauss (fig.1.1).
se obtine curba de distributie
cunoscuta si sub numele de clopotul lui Gauss (fig.1.1).
Graficul
functiei a fost obtinut reprezentand pe axa absciselor erorile 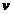 , iar pe axa ordonatelor
probabilitatiile
, iar pe axa ordonatelor
probabilitatiile 
 Probabilitatea va fi infinita zimala daca suprafata
masurata se imparte la suprafata cuprinsa intre curba si
axa -
Probabilitatea va fi infinita zimala daca suprafata
masurata se imparte la suprafata cuprinsa intre curba si
axa -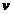
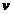 (considereta egala
cu unitatea).
(considereta egala
cu unitatea).
Respectiv:
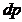 =
=


Integrand obtinem
 =
=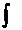


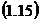
Probabilitatea de a avea scara cuprinsa intre -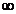 si
si 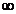 este 1, adica
certitudinea, este
este 1, adica
certitudinea, este

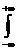

 = 1
= 1 
Printr-o
schimbare de varibila:
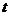 =
= 


Otinem:
 =
=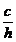
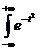


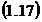
Integrala
lui Poisson este:
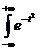
 =
= 
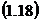
Cu
care egalitatea 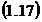 , resulta:
, resulta:
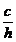

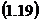
si


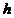 - indicele de precizie
- indicele de precizie 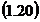
Folosind
relatia 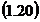 in
in
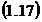 se obtine:
se obtine:
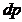

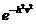


Egalitatea  este
valabila si in cazul in care consideram erorile
este
valabila si in cazul in care consideram erorile
adevarate  , deci
, deci
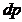

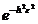
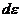

Se
ia in considerare modul de definire al probabilitatii si vom
scrie

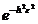
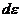 =
= 
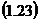
Sau:

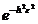

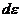
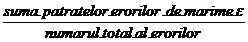

Integrand intre -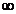 si +
si +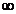 rezulta
rezulta



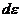

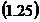
in care  este media patratelor erorilor
este media patratelor erorilor  , care
poate fi scrisa sub forma:
, care
poate fi scrisa sub forma:

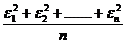

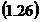
si care prin definitie reprezinta eroarea medie
patratica a unei singure masuratori.
Revenind
la egalitatea  , putem
scrie:
, putem
scrie:


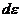

Dupa derivare in raport
cu 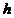 , obtinem
, obtinem



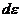

Din egalitatiile  si
si 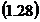 , putem
scrie:
, putem
scrie:
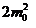

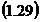
de unde:


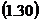
Din egalitatea
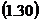 se observa ca
se observa ca 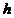 reprezinta indicele de precizie, invers
proportional cu eroarea medie patratica a unei singure
masuratori.
reprezinta indicele de precizie, invers
proportional cu eroarea medie patratica a unei singure
masuratori.
Practic, se noteaza  =
= si:
si:
 =
=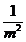

Numarul  este intotdeauna pozitiv si se numeste ponderea
masuratorii
este intotdeauna pozitiv si se numeste ponderea
masuratorii
efectuate.
Eroarea probabila, eroare
limita, eroare relativa, toleranta
Eroarea probabila  a unei
singure masuratori este eroarea pentru care numarul erorilor mai
mari este egal cu numarul erorilor mai mici ca ea.
a unei
singure masuratori este eroarea pentru care numarul erorilor mai
mari este egal cu numarul erorilor mai mici ca ea.
Daca se ordoneaza un sir de
observatii in succesiune crescatoare a valorilor erorilor accidentale,
eroarea probabila se va gasi in mijlocul acestui sir si
corespunde observatiei respective.
Astfel,
daca asupra unei lungimi au fost efectuate 9 observatii cu valorile:
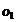 =38,245m
=38,245m 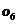 =38,248m
=38,248m
 =38,243m
=38,243m  =38,242m
=38,242m
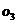 =38,247m
=38,247m  =38,249m
=38,249m
 =38,246m
=38,246m  =38,241m
=38,241m
 =38,244m
=38,244m
Media lor
aritimetica este M = 38,245m fata de
care erorile vor fi
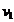

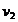 = -2
= -2  = -3
= -3
 = +2
= +2 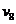 = +4
= +4
 = +1
= +1 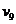 = -4
= -4
 = -1
= -1
Se ordoneaza
observatiile in succesiunea crescatoare a valorilor absolute a erorilor si obtinem
observatiile 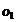 cu eroarea 0;
cu eroarea 0;
observatiile  si
si  cu
eroarea de +1;
cu
eroarea de +1;
observatiile  si
si 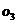 cu
eroarea de +2;
cu
eroarea de +2;
observatiile 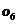 si
si  cu
eroarea de +3;
cu
eroarea de +3;
observatiile  si
si  cu
eroarea de +4.
cu
eroarea de +4.
Se
observa ca eroarea egala cu +2 reprezinta eroarea
probabila.
Utilizand calculul probabilitatilor
se poate stabili o legatura intre eroarea unei singure
masuratori si eroarea probabila de forma:
 =
= 

De
asemenea, tot pe baza calculului probabilitatiilor
se deduce ca probabilitatea ca eroare a unei singure masuratori
sa nu depaseasca 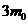 este de
este de  ceea ce inseamna
0 cazuri la o suta cazuri favorabile,
adica practic nici un caz.
ceea ce inseamna
0 cazuri la o suta cazuri favorabile,
adica practic nici un caz.
S-a
convenit, sa se ia eroarea a carei valoare este 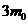 drept eroare
maxima sau eroare limita notata cu
drept eroare
maxima sau eroare limita notata cu 
Deci:
 =
=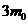

egalitate
valabila cand numarul de masuratori nu depaseste
100, ceea ce practic este indeplinit.
Daca
notam cu 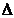 ecartul valorilor
masuratorilor (diferenta intre doua observtii),
rezulta ca va conduce la producerea a doua erori, la care probabilitatea va fi de 0,4, deci
practic nici un caz favorabil dintr-o suta de masuratori.
ecartul valorilor
masuratorilor (diferenta intre doua observtii),
rezulta ca va conduce la producerea a doua erori, la care probabilitatea va fi de 0,4, deci
practic nici un caz favorabil dintr-o suta de masuratori.
O
valoare maxima a acestui ecart  (diferenta intre doua valori extreme) care
reprezinta toleranta masuratorilor
(diferenta intre doua valori extreme) care
reprezinta toleranta masuratorilor  nu va depasi
nu va depasi
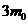 . Deci:
. Deci:


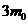
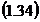
Practic se
verifca daca:


 (
( =
=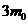 )
) 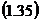
Au fost folosite
eroarea
medie patratica a unei singure masuratori;
eroarea
probabila;
eroarea limita.
Acestea
provin din masurarea unor marimi concrete si se exprima
prin aceleasi unitati de masura ca si
marimile respective.
Acolo
unde precizia masuratorilor este functie de marimea care se
masoara, cum este cazul masuratorilor de distante,
erorile care caracterizeaza complet rezultatul masuratorii in
ceea ce priveste gradul de precizie, sunt erorile relative.
Prin definitie eroarea
relativa 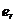 este:
este:
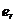 =
=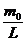

sau
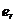 =
=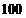
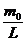 %
% 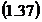
Prezentarea rezultatului masuratorilor
Rezultatul
masuratorilor efectuate asupra unei marimi se prezinta sub
forma:
X=
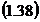
in care :
X - este valoarea adevarata
a marimii masurate;
 - valoarea
medie sau valoarea probabila;
- valoarea
medie sau valoarea probabila;
 - una din erorile definite (
- una din erorile definite ( ) sau
) sau  (eroarea medie
patratica a valorii
(eroarea medie
patratica a valorii 
Daca
asupra unei marimi a fost efectuata o singura observatie, in
relatia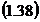
 -
valoarea observatiei;
-
valoarea observatiei;
 - eroarea observatiei (eroarea instrumentului
in principal).
- eroarea observatiei (eroarea instrumentului
in principal).
Semnificatia
egalitatii 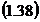 consta in aceea ca valoarea
adevarata a marimii masurate se afla intr-un interval
de precizie dat de inegalitatile :
consta in aceea ca valoarea
adevarata a marimii masurate se afla intr-un interval
de precizie dat de inegalitatile :

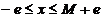

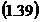
1.9 Consecintele formulei lui Gauss
Presupunem
ca asupra unei marimi au fost efectuate mai multe observatii,
carora le corespund erorile aparente respective.
Probabilitatea
aparitiei simultan a acestor erori va fi
 =
=

Sau
 =
= 
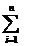
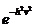
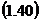
Probabilitatea va avea o valoare maxima atunci cand
 minin
minin
sau
 minin
minin 
Egalitatea  exprima principiul micilor patrate.
exprima principiul micilor patrate.
In
baza acestui principiu se determina
valorile probabile a marimilor masurate indiferent de
categoria de masuratori din care fac parte.




