Structuri
si tablouri de valori
Structurile,
sau tablourile de valori, sunt extensii ale matricilor bi-dimensionale.
Structurile sunt utile pentru construirea tabelelor de valori. De exemplu,
considerand vectorul:
» n =
(0:9)';
atunci, cu secventele urmatoare, se pot genera doua tabele de valori:
» tabel_puteri = [n n.^2 2.^n] <Enter>
tabel_puteri =
0 0 1
1 1 2
2 4 4
3 9 8
4 16 16
5 25 32
6 36 64
7 49 128
8 64 256
9 81 512
» x =
(1:0.1:2)'; logaritmi_si_exponentiale = [x log10(x) log(x) exp(x)]
logaritmi_si_exponentiale =
1.0000 0 0 2.7183
1.1000 0.0414 0.0953 3.0042
1.2000 0.0792 0.1823 3.3201
1.3000 0.1139 0.2624 3.6693
1.4000 0.1461 0.3365 4.0552
1.5000 0.1761 0.4055 4.4817
1.6000 0.2041 0.4700 4.9530
1.7000 0.2304 0.5306 5.4739
1.8000 0.2553 0.5878 6.0496
1.9000 0.2788 0.6419 6.6859
2.0000 0.3010 0.6931 7.3891
Structurile de date sunt definite
diferentiat, dar esenta problemei pe care o reprezinta este
aceeasi: sunt stocate seturi de date in conteinere diferite, definite ca pagini sau canale de achizitie. Utilitatea structurilor de date si
valori consista in aceea ca sunt manipulate volume mari de elemente
si pot fi manevrate pe principii si reguli aplicabile matricilor
si vectorilor.
Structuri
multidimensionale
Structurile multidimensionale se deosebesc de matrici
si tablouri de valori prin numarul de dimensiuni. In timp ce
matricile si tablourile de valori sunt caracterizate prin doua
dimensiuni (linii si coloane), structurile multidimensionale
dimensiuni suplimentare: paginile. De exemplu, cu secventa urmatoare genereaza
o retea cu 3 linii, 4 coloane si 5 pagini
»
R = randn(3,4,5)
R(:,:,1)
=
0.0000 -1.8740 0.7310 0.6771
-0.3179 0.4282 0.5779 0.5689
1.0950 0.8956 0.0403 -0.2556
R(:,:,2)
=
-0.3775 -0.2340 1.4435 0.7990
-0.2959 0.1184 -0.3510 0.9409
-1.4751 0.3148 0.6232 -0.9921
R(:,:,3)
=
0.2120 -0.7420 0.3899 -0.5596
0.2379 1.0823 0.0880 0.4437
-1.0078 -0.1315 -0.6355 -0.9499
R(:,:,4)
=
0.7812 -0.2656 0.9863 0.2341
0.5690 -1.1878 -0.5186 0.0215
-0.8217 -2.2023 0.3274 -1.0039
R(:,:,5)
=
-0.9471 -1.0559 -1.2173 -1.3493
-0.3744 1.4725 -0.0412 -0.2611
-1.1859 0.0557 -1.1283 0.9535
iar cu secventa:
» p = perms(1:4); A = magic(4); M = zeros(4,4,24);
»
for k = 1:24
M(:,:,k) =
A(:,p(k,:))
End
se
genereaza o retea cu 4 linii,
4 coloane si 24 pagini. Aceasta retea este
reprezentata succint in figura urmatoare (la rularea secventei
anterioare se vor afisa toate paginile structurii M, pentru fiecare valoare a indexului k):

Operatiile aritmetice
cu tablouri de valori
Tablourile
sunt seturi de valori ordonate, dupa sistemul "matricial":linii si
coloane. MATLAB opereaza in mod diferit cu tablourile fata de
matrici, deosebirile evidente se observa la inmultire si
impartire, iar conditia esentiala pentru realizarea
unei operatii cu tablouri de valori este aceea ca tablourile trebuie
sa fie de aceeasi dimensiune.
Operatiile
cu tablouri sunt operatii aritmetice (inmultire, impartire,
ridicare la putere, etc.) intre elementele situate in aceeasi pozitie
a tablourilor, cunoscute sub numele de operatii
element cu element.
Daca,
in loc de unul dintre operanzi este un scalar, acesta opereaza cu fiecare
element al tabloului.
Pentru a
preciza ca operatiile de inmultire, impartire,
ridicare la putere (exclus adunarea si scaderea) se efectueaza
element cu element intre componentele a doua tablouri de valori (matrici, seturi ordonate de valori,
etc.) de aceleasi dimensiuni,
se utilizeaza operatorul pentru operatia dorita, precedat de
caracterul punct (exclus cazul adunarii si scaderii, care sunt
similare celor pentru matrici):
pentru inmultire- " .* "
pentru impartire - " ./ " sau " . "
pentru ridicare la putere - " .^ "
Adunarea
si scaderea
tablourilor
de valori
Pentru ca
adunarea si scaderea sa se poata efectua este necesara
indeplinirea conditiei de identitate a dimensiunilor tablourilor care
opereaza.
Ex.:
Fie : , b=
, b=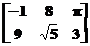 , c=10, d=
, c=10, d=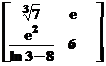 .
.
Sa se calculeze: a-b;
a-c; c-a; c-b; a+d
Cu secventa MATLAB:
» a=[1,2,3;4,5,6]; b=[-1,8,pi;9,sqrt(5),3];
c=10;
»
d=[7^(1/3),exp(1);exp(2)/(log(3)-8),6];
» A=a-b [Enter]
A =
2.0000 -6.0000 -0.1416
-5.0000 2.7639 3.0000
» B=a-c [Enter]
B =
-9 -8 -7
-6 -5 -4
» C=c-a [Enter]
C =
9 8 7
6 5 4
» D=c-b [Enter]
D =
11.0000 2.0000 6.8584
1.0000 7.7639 7.0000
»
E=a+d Enter]
In cazul E=a+d, MATLAB returneaza un mesaj de
eroare, intrucat nu este indeplinita conditia de identitate a
dimensiunilor celor doi operanzi:
??? Error using ==> +
Matrix dimensions must agree..
???
Eroare la utilizarea operatorului « + »
Matricile trebuie sa
aiba aceleasi dimensiuni
Inmultirea
tablourilor de valori
Pentru ca inmultirea a
doua tablouri de valori sa se realizeze, este obligatorie
conditia ca acestea sa fie strict de aceeasi dimensiune :
Ex.:
Fie : , b=
, b=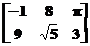 ,c=10,d=
,c=10,d=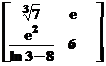 .
.
Sa se calculeze: produsele:ab;ac;ca;cb; ad
Cu secventa MATLAB:
» a=[1,2,3;4,5,6]; b=[-1,8,pi;9,sqrt(5),3];
c=10;
»
d=[7^(1/3),exp(1);exp(2)/(log(3)-8),6];
» A=a.*b [Enter]
A =
-1.0000 16.0000 9.4248
36.0000 11.1803 18.0000
» B=a.*c [Enter]
B =
10 20 30
40 50 60
» C=c.*a [Enter]
C =
10 20 30
40 50 60
» D=c.*b [Enter]
D =
-10.0000 80.0000 31.4159
90.0000 22.3607 30.0000
In cazul E=a.*d, MATLAB returneaza un mesaj de
eroare, intrucat cele doua tablouri au dimensiuni diferite:
»
E=a.*d
??? Error using ==> .*
Matrix dimensions must agree.
???
Eroare la utilizarea operatorului « + »
Matricile
trebuie sa aiba aceleasi dimensiuni
Impartirea
la dreapta a
tablourilor
de valori
Impartirea
la dreapta, a doua tablouri, este simbolizata prin caracterul
combinat " ./ " (punct + slash).
Ex.:
Fie : , b=
, b=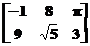 , c=10.
, c=10.
Sa se calculeze: a:b;a:c;c:a;c:b.
Rezolvare:
Cu secventa
MATLAB:
» a=[1,2,3;4,5,6]; b=[-1,8,pi;9,sqrt(5),3];
c=10;
» d=a./b [Enter]
d =
-1.0000 0.2500 0.9549
0.4444 2.2361 2.0000
» e=a./c [Enter]
e =
0.1000 0.2000 0.3000
0.4000 0.5000 0.6000
» f=c./a [Enter]
f =
10.0000 5.0000 3.3333
2.5000 2.0000 1.6667
» g=c./b [Enter]
g =
-10.0000 1.2500 3.1831
1.1111 4.4721 3.3333
Impartirea
la stanga
Operatia
de impartire la stanga, intre doua tablouri de aceleasi dimensiuni
este simbolizata cu operatorul " .
" (punct + backslash):
x=y.z
si reprezinta catul dintre elementul z(i,j) si elementul
y(i,j), adica: x=y.z=z./y.
Ex.:
Fie : , b=
, b=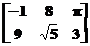 , c=10.
, c=10.
Sa se calculeze:a.b;a.c;c.a;c.b.
Solutie:
Cu secventa MATLAB:
» a=[1,2,3;4,5,6]; b=[-1,8,pi;9,sqrt(5),3];
c=10;
» d=a.b [Enter]
d =
-1.0000 4.0000 1.0472
2.2500 0.4472 0.5000
» e=a.c [Enter]
e =
10.0000 5.0000 3.3333
2.5000 2.0000 1.6667
» f=c.a [Enter]
f =
0.1000 0.2000 0.3000
0.4000 0.5000 0.6000
» g=c.b [Enter]
g =
-0.1000 0.8000 0.3142
0.9000 0.2236 0.3000
Ridicarea la putere a
tablourilor de valori
Operatia
de ridicare la putere a tablourilor de valori este simbolizata prin
caracterul combinat (« .^ « ). Astfel, instructiunea A=B.^C, reprezinta calculul
puterii unui element al matricei B,
unde exponentul este elementul de pe pozitia corespunzatoare din
matricea C: adica elementul A(i,j) este obtinut prin ridicarea
la puterea C(i,j) a elementului B(i,j).
Ex.:
Fie : , b=
, b=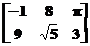 , c=10.
, c=10.
Sa se calculeze : ab; ac;
ca; cb.
Rezolvare:
Cu secventa MATLAB:
» a=[1,2,3;4,5,6]; b=[-1,8,pi;9,sqrt(5),3];
c=10;
» d=a.^b [Enter]
d =
1.0000e+000 2.5600e+002 3.1544e+001
2.6214e+005 3.6555e+001 2.1600e+002
» e=a.^c [Enter]
e =
1 1024 59049
1048576 9765625 60466176
» f=c.^a [Enter]
f =
10 100 1000
10000 100000 1000000
» g=c.^b [Enter]
g =
1.0e+009 *
0.0000 0.1000 0.0000
1.0000 0.0000 0.0000
Transpunerea tablourilor de valori
Operatia
de transpunere a unui tablou este simbolizata de operatorul combinat ".' "
(punct-apostrof). In acest mod liniile tabloului devin coloane si
invers.
Ex.:
Sa
se determine transpusa tabloului 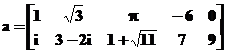 .
.
Cu
secventa MATLAB:
» a=[1,
sqrt(3),pi,-6,0;I,3-2*I,1+sqrt(11),7,9]; [Enter]
» a1=a.' [Enter]
a1 =
1.0000 0 + 1.0000i
1.7321 3.0000 - 2.0000i
3.1416 4.3166
-6.0000 7.0000
0 9.0000
Siruri de caractere
Matrici din siruri
de caractere
Un tip, aparte, de date
utilizate de MATLAB il constituie sirurile
de caractere. Acestea pot fi manipulate ca oricare alt tip de date stocate
de orice limbaj de programare. Figura urmatoare prezinta tipurile de
date utilizate de MATLAB.
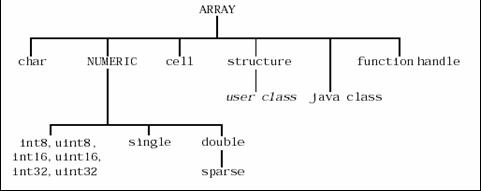
Tipuri de date utilizate de MATLAB
Crearea matricior cu
siruri de caractere
Sirurile
de caractere sunt stocate in MATLAB ca tablouri de valori, reprezentate prin
coduri numerice (codul numeric ASCII). Datele de tip sir de caractere sunt introduse prin plasarea caracterelor
respective intre doua caractere apostrof « ' » .
Codurile ASCII sunt
afisate cu functia MATLAB double() :
»
coduri_ASCII_litere_mici=double('abcdefghijklmnopqrstuvwxz')
coduri_ASCII_litere_mici =
Columns 1 through 11
97 98 99 100 101 102 103 104 105 106 107
Columns 12 through 22
108 109 110 111 112 113 114 115 116 117 118
Columns 23 through 25
119 120 122
»coduri_ASCII_majuscule=double('abcdefghijklmnopqrstu vwxz')
coduri_ASCII_
majuscule =
Columns 1 through 11
65 66 67 68 69 70 71 72 73 74 75
Columns 12 through 22
76 77 78 79 80 81 82 83 84 85 86
Columns 23 through 25
87 88 90
De exemplu, urmatoarea secventa MATLAB introduce
tabloul nume, avand dimensiunea 1x17 si matricea functia cu dimensiunea 1x24:
» nume='Popescu J. Eduard'
nume =
Popescu J. Eduard
» functia='Director
General Adjunct'
functia =
Director General Adjunct
Daca
se listeaza, caracteristicile matricei nume, cu functia who,
se constata:
» whos
nume
Name Size Bytes Class
nume 1x17 34 char array
adica : matricea nume
are dimensiunea 1x17, se
stocheaza in memorie ocupand 34
biti si este din classa char
array (tablou de caractere).
Matricile
de caractere se pot concatena pentru crearea unei noi matrici, folosind
functia MATLAB strcat() sau
operatorul MATLAB de concatenare [ ]. De exemplu, pentru concatenarea celor doua tablouri de mai
sus, se foloseste secventa MATLAB :
»
Nume_si_Functia=strcat(nume,',',functia)
Nume_si_Functia
=
Popescu
J. Eduard,Director General Adjunct
» whos Nume_si_Functia
Name Size Bytes Class
ans 1x42 84 char array
Grand total is 42 elements using 84 bytes
Concatenarea a doua tablouri pentru transformarea intr-o
matrice cu doua linii, se foloseste algoritmul de introducere a
datelor ca matrice (paranteze drepte):
» numele_si_functia=['Popescu J.
Eduard ';'Director General Adjunct']
numele_si_functia =
Popescu J. Eduard
Director General Adjunct
» whos numele_si_functia
Name Size Bytes Class
numele_si_functia 2x24 96 char array
Grand total is 48 elements using 96 bytes
Se
observa diferenta fata de cazul afisarii textului
intr-o singura linie:matricea noua avand dimensiunea 2x24, fata de o linie cu 42 elemente
la prima varianta, iar pentru stocare sunt ocupati 96 biti de memorie,
fata de 84 in prima varianta, classa este aceeasi char array.
Conversia
sirurilor de caractere
in
coduri numerice
Matricile
cu siruri de caractere stocheaza fiecare caracter in coduri numerice pe 16 biti.
Codurile ASCII ale caracterelor alfanumerice sunt prezentate in tabelul
urmator :
|
Cod
|
Caracter
|
Cod
|
Caracter
|
Cod
|
Caracter
|
Cod
|
Caracter
|
Cod
|
Caracter
|
|
(zero)
|
|
|
|
|
|
N
|
|
h
|
|
|
|
|
|
|
|
O
|
|
i
|
|
|
|
|
|
|
|
P
|
|
j
|
|
|
|
|
|
|
|
Q
|
|
k
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R
|
|
l
|
|
|
|
|
|
|
|
S
|
|
m
|
|
|
|
(blank)
|
|
|
|
T
|
|
n
|
|
|
|
|
|
|
|
U
|
|
o
|
|
|
|
|
|
<
|
|
V
|
|
p
|
|
|
|
|
|
|
|
W
|
|
q
|
|
|
|
|
|
>
|
|
X
|
|
r
|
|
|
|
|
|
|
|
Y
|
|
s
|
|
|
|
&
|
|
|
|
Z
|
|
t
|
|
|
|
|
|
A
|
|
|
|
u
|
|
|
|
|
|
B
|
|
|
|
v
|
|
|
|
|
|
C
|
|
|
|
w
|
|
|
|
|
|
D
|
|
|
|
x
|
|
|
|
|
|
E
|
|
|
|
y
|
|
|
|
|
|
F
|
|
|
|
z
|
|
|
|
|
|
G
|
|
a
|
|
|
|
|
|
|
|
J
|
|
d
|
|
|
|
|
|
|
|
K
|
|
e
|
|
|
|
|
|
|
|
L
|
|
f
|
|
|
|
|
|
|
|
M
|
|
g
|
|
|
MATLAB
utilizeaza functia double()
pentru convertirea sirului de caractere in coduri numerice a acestora,
respectiv functia char() pentru
reprezentarea acestor valori in sir de caractere:
» nume_si_functia_numeric=double(nume_si_functia)
nume_si_functia_numeric =
Columns 1 through 12
80 111 112 101 115 99 117 32 74 46 32 69
68 105 114 101 99 116 111 114 32 71 101 110
Columns 13 through 24
100 117 97 114 100 32 32 32 32 32 32 32
101 114 97 108 32 65 100 106 117 110 99 116
Se
observa ca matricea "nume_si_functia" (cu 2 linii si 24 coloane) a fost convertita intr-o matrice cu aceleasi dimensiuni dar in
reprezentare numerica, nume_si_functia_numeric.
De exemplu, pentru verificare, se poate folosi urmatoarea
secventa:
»valoarea_numerica_a_literei_P=double('P')
valoarea_numerica_a_literei_P =
80
»valoarea_numerica_a_literei_o=double('o')
valoarea_numerica_a_literei_o =
111
Pentru revenirea la forma anterioara (matrice cu
caractere) se foloseste secventa:
» nume_si_functia=char(nume_si_functia_numeric)
nume_si_functia =
Popescu J. Eduard
Director General Adjunct
Codurile
ASCII, sunt convertite in caractere folosind functia MATLAB char() :
» char(65:75)
ans =
ABCDEFGHIJK
Se pot
folosi functiile char() si
double() pentru a genera siruri
identice de caractere, adica:
» char(ones(4,20)*double('#'))
ans =
####################
####################
####################
####################
Aceasta instructiune se executa
astfel :
-functia ones(4,20) genereaza patru linii si 20 de coloane in care
elementele sunt cifrele 1;
-multiplicand prin double('#') aceasta matrice, elementele "1" sunt inlocuite cu codul ASCII al unui caracter oarecare (in
acest caz este codul caracterului "#"),
iar functia char()
converteste aceste coduri in caractere (caracterul "#").
Daca
o variabila- caracter
este implicata intr-o operatie aritmetica, MATLAB
utilizeaza codul ascii al
caracterului, pentru efectuarea calculelor. Astfel, daca :
» p='m';
atunci expresia:
» p+2
returneaza rezultatul:
ans =
111
Operatiile
cu matrici si tablouri de valori pot fi extinse la sirurile de
caractere. De exemplu, daca p
este un sir de caractere (in cazul de fata m), atunci expresia char(p+1)
returneaza litera urmatoare din alfabet.
Relatia
dintre caractere si codurile ASCII, ale acestora, permite efectuarea
operatiilor aritmetice cu acestea. De exemplu, instructiunea
urmatoare va realiza impartirea numarului reprezentand
codul ASCII al caracterului « < »
(cod 60), la numarul reprezentand codul ASCII al caracterului « x » (120) :
» double('<')/double('x')
ans =
0.5000
Sirurile
de caractere pot fi afisate folosind functia MATLAB fprintf(), cu specificatorul de format « %s », fiind posibila, de asemenea, aranjarea « la dreapta »,
« la stanga » sau « egal distantata »
(« justified »), respectiv « trunchiata ». Cu
instructiunile urmatoare se afiseaza cuvintele
« IMPARATUL NAPOLEON I », in diferite variante :
» fprintf('%40s In','IMPARATUL
NAPOLEON')
IMPARATUL NAPOLEON I
» fprintf('%-40s In','IMPARATUL
NAPOLEON')
IMPARATUL NAPOLEON I
» fprintf('%20s In','IMPARATUL
NAPOLEON')
IMPARATUL NAPOLEON I
» fprintf('%-20s In','IMPARATUL
NAPOLEON')
IMPARATUL NAPOLEON I
» fprintf('%60s In','IMPARATUL
NAPOLEON')
IMPARATUL NAPOLEON I
» fprintf('%30s In','IMPARATUL
NAPOLEON')
IMPARATUL NAPOLEON I
Compararea sirurilor de caractere
Sirurile
de caractere se compara prin codurile ASCII. Astfel, sirurile « ann" si « ban », se compara folosind operatorii relationali (<, <=, >, >=, ==, ~=), similar
matricilor :
»s1='ann'; s2='ban';
»s1<s2
ans =
1 0 0
Daca sirurile nu au
aceeasi dimensiune (acelasi numar de caractere), folosirea
operatorilor relationali este improprie, MATLAB afisand un mesaj de
eroare :
» s3='anna';
» s2='ban';
» s3>s2
??? Error using ==>
>
Array dimensions must
match for binary array op.
??? Eroare la utilizarea operatorului >
Dimensiunile
structurilor trebuie sa corespunda pentru efectuarea operatiilor binare
Compararea
sirurilor cu dimensiuni diferite se realizeaza cu functia MATLAB
strcmp(si,sj), care va afisa
valoarea logica 1, daca
cele doua siruri sunt identice, respectiv, valoarea logica 0, daca cele doua siruri
au valori diferite ale codurilor ASCII:
» strcmp(s2,s3)
ans =
0
Functiile
specifice operatiilor si operatiunilor cu siruri de
caractere sunt prezentate folosind :
» help
matlabstrfun
siruri de caractere bidimensionale
Sirurile
de caractere bi-dimensionale se pot crea exact ca si matricile, cu
exceptia faptului ca fiecare linie trebuie sa aiba
acelasi numar de caractere (acelasi numar de coloane), in
caz contrar se va afisa un mesaj de eroare care avertizeaza
utilizatorul asupra acestui aspect (rezolvarea problemei este simpla
daca se introduce un numar necesar de spatii libere,
blank-uri) :
» nume_si_adresa=['Albert
Durrer ';'21 Bruxelles Ave';'New York ']
nume_si_adresa =
Albert
Durrer
21
Bruxelles Ave
New
York
» numesiadresa=['Albert Durrer';'21
Bruxelles Ave';'New York']
??? Error using ==> vertcat
All rows in the bracketed expression
must have the same
number of columns.
???
Eroare la utilizarea vertcat(concatenarea
verticala)
Toate liniile,
inaranteze drepte, trebuie sa aiba acelasi numar de coloane
O
metoda simpla pentru realizarea structurilor bi-dimensionale, cu
siruri de caractere, este aceea folosind functia MATLAB char(), care seteaza automat numarul
de coloane necesare pe fiecare linie:
nume_si_adresa=char('Albert
Durrer','21 Bruxelles Ave','New York')
nume_si_adresa =
Albert
Durrer
21 Bruxelles Ave
New York
De
observat ca daca structura nume_si_adresa
se apeleaza cu subscript, pentru extragerea elementelor, acestea sunt
afisate in ordinea clasica a vectorilor liniari (vectori
coloana), elementele fiind « citite » pe coloana incepand
cu primul element al coloanei intai :
» numesiadresa=['Albert Durrer ';'21 Bruxelles Ave';'New York ']
numesiadresa =
Albert
Durrer
21
Bruxelles Ave
New
York
» numesiadresa(1:3)
ans =
A2N
» numesiadresa(1:4)
ans =
A2Nl
» numesiadresa(1:20)
ans =
A2Nl1eb weB rrYtuo x
EVALUAREA SIRURILOR DE CARACTERE
Daca
o expresie MATLAB este « codata » ca sir de caractere de
variabila « t », de
exemplu, atunci functia eval(t)
va genera evaluarea expresiei in « t »
(adica, sirul de caractere va fi interpretat).
Aceasta facilitate se numeste text
macro. De exemplu, instructiunea urmatoare :
» s='x=-b/(2*a)';b=8;a=7;
» eval(s)
x =
-0.5714
Utilizarea
functiei eval() este foarte
practica in situatii in care sunt solicitate date de intrare, cum ar
fi cazul unor reprezentari grafice :
» x=0:0.01:10;
» f=input('Introduceti functia de
variabila x pentru reprezentare grafica:','s')
Introduceti functia de variabila x
pentru reprezentare grafica:
exp(-0.5*x).*sin(x);
» plot(x,eval(f)),grid
Dupa
introducerea functiei MATLAB input()
apare linia de comanda « de asteptare », prin care
utilizatorul este invitat sa introduca expresia functiei de
variabila « x » :
Introduceti functia de variabila x pentru
reprezentare grafica:
Daca
utilizatorul introduce o expresie in care nu exista date care pot fi
evaluate, MATLAB afiseaza un mesaj de eroare, altfel este
evaluata expresia in
variabila « x » ,
si reprezentata grafic pentru valorile date :

Structurile
definite, pana acum, in MATLAB, au avut elementele date ori numai ca
numere, ori numai ca siruri de caractere. MATLAB permite definirea
structurilor de date prin introducerea diferitelor tipuri de date in diferite
campuri. De exemplu, se poate crea o structura, numita « student » (de exemplu), cu un camp
alocat numelui :
» student.nume='Juan Antonio Cajigal';
un alt camp pentru seria si numarul de
legitimatie:
» student.legitimatie='JUANCA0123';
respectiv, un camp pentru calificativele primite :
» student.calificative=[7 9 6 5];
Pentru a
vedea intreaga structura, se introduce, de la tastatura, in linia de
comanda, numele acesteia:
» student
student =
nume: 'Juan Antonio Cajigal'
legitimatie: 'JUANCA0123'
calificative: [7 9 6 5]
Apelarea
unui element al structurii se realizeaza folosind aceeasi metodologie
ca si in cazul matricilor si tablourilor de valori. De exemplu,
afisarea celei de-a doua note, respectiv a celei de-a patra, este
realizabila prin introducerea de la tastatura, in linia de
comanda, a numelui campului, si ca subscript (in paranteze, pentru
stabilirea pozitiei in matricea linie), pozitia acesteia in matricea
respectiva, student.calificative(i):
» student.calificative(2)
ans =
9
» student.calificative(4)
ans =
5
De notat ca folosirea caracterului ".",
pentru separarea numelui unei structuri, la crearea sau apelarea acesteia, este
esentiala.
Pentru
adaugarea unor elemente suplimentare la structura creata, se vor
folosi indici de subscriere, dupa numele structurii:
» student(2).nume='Luis
Jimenez';
» student(2).legitimatie='LUJIM0012';
» student(2).calificative=[7
5];
In
structura cu numele"student"
campurile alocate primului nume, vor putea fi accesate folosind indicele de
subscriere 1, dupa numele
structurii "student":
» student(1)
ans =
nume: 'Juan Antonio Cajigal'
legitimatie: 'JUANCA0123'
calificative: [7 9 6 5]
Este de
observat ca nu este necesar ca o structura sa aiba
dimensiunile campurilor identice: campul "calificative"
are dimensiunea 4 la "student(1)", in timp ce, la "student(2)" campul are dimensiunea 2.
Structura
cu numele "student", are acum
dimensiunea 1x2:are doua
elemente ("student(1)" si "student(2)"), fiecare dintre acestea
avand cate 3 campuri. Daca o structura are definite mai multe
elemente, MATLAB nu afiseaza continutul fiecarui camp,
atunci cand aceasta este apelata cu numele simplu. Astfel, daca
structura "student" se apeleaza
in linia de comanda, simplu, fara subscript, atunci se va
afisa un sumar exhaustiv:
»student
student =
1x2 struct array with
fields:
nume
legitimatie
calificative
Un sumar
asemanator este afisat daca se apeleaza functia
MATLAB fieldnames():
» fieldnames(student)
ans =
'nume'
'legitimatie'
'calificative'
Pre-alocarea
campurilor si definirea unei structuri se poate realiza folosind si
functia MATLAB struct().
Campul
unei structuri poate contine orice tip de date, chiar si o alta
structura. De exemplu, se poate crea o structura, fie numele acesteia
"cursuri", care sa
contina date privind cursurile sustinute de studenti, in
care un camp va fi alocat titlului cursului, si alt camp va contine
structura "student", creata
anterior:
» cursuri.titlu='Metode numerice';
» cursuri.grupa=student;
» cursuri
cursuri =
titlu: 'Metode numerice'
grupa: [1x2 struct]
Se poate
aloca un al doilea element structurii "cursuri",
sa presupunem, pentru un alt curs:
» cursuri(2).titlu='Metode
numerice IMT';
» cursuri(2).grupa=student;
Pentru a
afisa titlurile cursurilor se foloseste instructiunea:
» cursuri(1:2).titlu
ans =
Metode numerice
ans =
Metode numerice IMT
Pentru a
se afisa numele studentilor participanti la cursuri, se
foloseste instructiunea:
» cursuri(1).grupa(1:2).nume
ans =
Juan Antonio Cajigal
ans =
Luis Jimenez
MATLAB
permite generarea unei liste cu "variabile separate prin virgula", prin
extragerea acestora din campurile structurii, folosind functia
specifica deal(). De exemplu,
pentru crearea unei liste continand numele studentilor
participanti la cursuri, se foloseste instructiunea:
» [nume1,nume2]=deal(cursuri(1).grupa(1:2).nume)
nume1 =
Juan Antonio Cajigal
nume2 =
Luis Jimenez
Pentru
stergerea sau anularea unor campuri ale structurii create se
foloseste functia MATLAB rmfield().
structuri celulare
Celula
este entitatea cea mai comuna in MATLAB. Celula poate fi asimilata cu
un "conteiner de date" care poate contine orice tip de date:tablouri de
valori numerice, sau siruri de caractere, structuri sau celule.
Definirea celulelor
Indexare:
Considerand
ca structura "student",
creata in paragraful anterior, exista stocata in memoria
calculatorului, se poate defini o structura celulara ("2x2") prin atribuirea datelor din celulele specificate:
» c(1,1)=;
» c(1,2)=;
» c(2,1)=;
» c(2,2)=;
» c
c =
[ 3x3 double ] [ 2x6 char ]
[ 13] [ 1x2 struct ]
In aceasta grupare de
instructiuni, parantezele rotunde din partea stanga a semnului de
atribuire ("="), au acelasi rol
ca si in cazul tablourilor de valori, sau al matricilor, avand
semnificatia de referire la un
anumit element al structurii celulare. Ceea ce diferentiaza
structurile celulare de tablourile de valori, este utilizarea parantezelor
acolade (""), in partea
dreapta a semnului de atribuire. Aceste caractere (""), folosite numai in partea dreapta a semnului de
atribuire, arata continutul unei celule, avand
rol de constructori ai
structurii celulare. Daca aceste caractere (""), sunt folosite in alte situatii, atunci acestea se
refera la elementul specificat in interiorul parantezelor. De exemplu,
instructiunea:
»cellplot(c)
afiseaza,
intr-o figura separata, structura celulara "c":

iar
instructiunea:
»celldisp(c)
afiseaza, in fereastra de comanda,
structura celulara "c":
c =
0.9501 0.4860 0.4565
0.2311 0.8913 0.0185
0.6068 0.7621 0.8214
c =
13
c =
Bonzai
Makay
c =
1x2 struct
array with fields:
nume
legitimatie
calificative
Apelarea,
in linia de comanda, a elementelor structurii celulare, se realizeaza
folosind parantezele acolade, in combinatii cu parantezele rotunde, sau
drepte. Astfel, apelarea celulei de pe pozitia 1, respectiv afisarea
continutului acestei celule, se realizeaza cu instructiunea:
»
c
ans
=
0.9501 0.4860 0.4565
0.2311 0.8913 0.0185
0.6068 0.7621 0.8214
Elementul de pe pozitia (2,3), al celulei 1, se
apeleaza cu instructiunea:
» c(2,3)
ans
=
0.0185
In mod similar,
sunt afisate celelalte celule ale structurii celulare "c":
» c
ans
=
13
» c
ans
=
Bonzai
Makay
» c
ans
=
1x2
struct array with fields:
nume
legitimatie
calificative
De observat ca elementele unei structuri
celulare sunt "citite" pe coloana.
Structuri celulare multidimensionale
Structurile celulare multidimensionale,
in MATLAB, sunt extensii normale ale matricilor bi-dimensionale.
Se reaminteste faptul ca matricile
sunt caracterizate prin cele doua dimensiuni:numarul de linii si numarul
de coloane. Astfel, in figura de mai jos se poate vedea ca, daca
fiecare locatie a grilei reprezinta un element al matricei, atunci, un
element al matricei poate fi accesat prin apelarea sa cu doi indici
reprezentand numarul liniei, respectiv al coloanei pe care acesta se
regaseste in matricea data. Structurile multidimensionale utilizeaza indici suplimentari pentru
apelarea unui element. Astfel, o structura tri-dimensionala
utilizeaza trei indici de
apel:
Primul indice reprezinta linia;
Al doilea indice reprezinta coloana;
Al treilea indice reprezinta pagina.
Reprezentarea schematica a unei structuri multidimensionale se regaseste in
figura urmatoare:

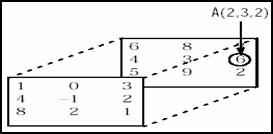 De exemplu, pentru apelarea unui element de pe linia 2, coloana 3 si pagina 2 (schema alaturata ),
se vor folosi trei indici de acces (2,3,2).
De exemplu, pentru apelarea unui element de pe linia 2, coloana 3 si pagina 2 (schema alaturata ),
se vor folosi trei indici de acces (2,3,2).
Daca
se adauga dimensiuni suplimentare unei structuri, atunci si
elementele vor fi accesate prin indici suplimentari. De exemplu, pentru o
retea cu patru dimensiuni se vor folosi patru indici:primii doi pentru
perechea linie-coloana si ultimii doi pentru a treia si a patra
dimensiune
Crearea structurilor
celulare multidimensionale
Pentru
crearea structurilor celulare multidimensionale se folosesc, in principiu,
tehnici similare celor pentru generarea matricilor bi-dimensionale. In plus,
specific structurilor multidimensionale,
MATLAB dispune de functii speciale de concatenare. Generarea structurilor celulare
multidimensionale este posibila prin:
A). Utilizarea
indexarii ;
B). Utilizarea
functiilor MATLAB ;
C). Utilizarea
functiei cat().
A). Generarea structurilor celulare multidimensionale prin indexare
O cale,
simpla, pentru crearea structurilor multidimensionale, este de a genera o matrice bidimensionala
si apoi aceasta sa fie extinsa. De exemplu, pentru a suplimenta,
dimensiunile unei matrici, cu o pagina noua, se procedeaza
astfel:
Considerand matricea 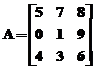 cu dimensiunea 3x3,
cu dimensiunea 3x3,
-se introduce de la tastatura matricea A:
»
A = [5 7 8; 0 1 9; 4 3 6];
-se suplimenteaza dimensiunea matricei A, adaugand o pagina:
»
A(:,:,2)= [1 0 4; 3 5 6; 9 8 7]
A(:,:,1) =
5 7 8
0 1 9
4 3 6
A(:,:,2) =
1 0 4
3 5 6
9 8 7
B). Generarea
structurilor multidimensionale prin
functii MATLAB
Se pot
foslosi functiile MATLAB, cum ar fi randn(),
zeros(), ones(), pentru generarea structurilor multidimensionale, exact ca in cazul matricilor
bi-
dimensionale:
» retea_arbitrara = randn(6,5,2)
retea_arbitrara(:,:,1) =
-0.1199 -0.0793 0.0359 0.1326 -1.0246
-0.0653 1.5352 -0.6275 1.5929 -1.2344
0.4853 -0.6065 0.5354 1.0184 0.2888
-0.5955 -1.3474 0.5529 -1.5804 -0.4293
-0.1497 0.4694 -0.2037 -0.0787 0.0558
-0.4348 -0.9036 -2.0543 -0.6817 -0.3679
retea_arbitrara(:,:,2) =
-0.4650 1.0378 1.9574 1.1902 0.0860
0.3710 -0.3898 0.5045 -1.1162 -2.0046
0.7283 -1.3813 1.8645 0.6353 -0.4931
2.1122 0.3155 -0.3398 -0.6014 0.4620
-1.3573 1.5532 -1.1398 0.5512 -0.3210
-1.0226 0.7079 -0.2111 -1.0998 1.2366
C). Generarea structurilor multidimensionale
cu functia MATLAB cat()
O metoda simpla pentru
generarea structurilor celulare
multidimensionale o constituie utilizarea functiei cat(), care concateneaza o lista de alte structuri pe mai
multe dimensiuni. Forma generala a functiei este: B = cat(dim,A1,A2), in care A1,A2, reprezinta lista de
structuri celulare multidimensionale,
iar dim, este dimensiunea:
» B = cat(3,[2 8 4 9;1 0 5 3],[1 3 3 5 ; 4 7 9 7])
B(:,:,1)
=
2 8 4 9
1 0 5 3
B(:,:,2) =
1 3 3 5
4 7 9 7
» a =
magic(3); b = pascal(3); c = cat(2,a,b)
c =
8 1 6 1 1 1
3 5 7 1 2 3
4 9 2 1 3 6
» a = magic(3); b = pascal(3); c
= cat(5,a,b)
c(:,:,1,1,1) =
8 1 6
3 5 7
4 9 2
c(:,:,1,1,2) =
1 1 1
1 2 3
1 3 6
Modificarea formei structurilor
celulare multidimensionale
Daca
nu se solicita schimbarea formei sau dimensiunilor, o retea
multidimensionala isi pastreaza caracteristicile
specificate atunci cand a fost creata. Dimensiunile structurii se pot
modifica prin stergerea sau adaugarea unor elemente, iar forma
structurii se poate schimba prin specificarea unui numar diferit de linii,
coloane sau pagini. Forma generala a functiei MATLAB pentru
modificarea formei unei structuri este:
R=reshape(A,[s1,s2,s3, . ]),
in care A este structura
a carei forma urmeaza a fi schimbata, iar s1,s2,s3, . , reprezinta noile
dimensiuni ale structurii cu forma schimbata. Schema de lucru a
functiei reshape() este
reprezentata in schitele de mai jos: (functia reshape() se foloseste si pentru tablouri mxn-dimensionale,
respectiv in cazul Sistemelor de Control sau ca bloc sursa pentru crearea
schemelor Simulink).
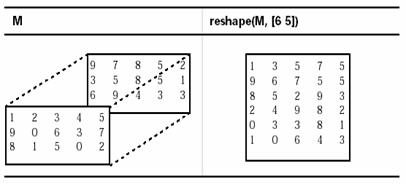
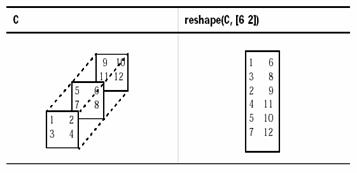
Schimbarea formei structurilor
Organizarea datelor in structurile
celulare multidimensionale
Structurile multidimensionale pot fi utilizate pentru
stocarea si reprezentarea datelor in doua moduri:
Ca plane
sau pagini cu date bi-dimensionale.
Acestea pot fi tratate ca matrici bi-dimensionale;
Ca date multivariabile sau multidimensionale. De
exemplu, se pot reprezenta structuri 4-dimensionale in care fiecare element
corespunde temperaturii sau presiunii aerului masurate intr-un set de
puncte ale unei incinte.
De exemplu, daca se
considera o imagine RGB, a carei matrice de culoare poate fi
reprezentata ca in figura de mai jos:

sau multimea
temperaturilor masurate intr-un numar egal de puncte:
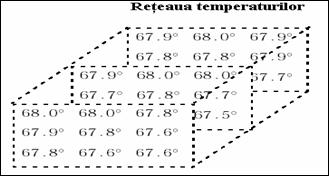
APLICATII
Ex.1:
Fie: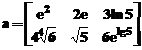 ,
,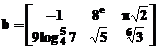 ,c=2
,c=2
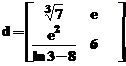
Sa se calculeze: a-b; a-c;
c-a; c-b; a+d
Ex.2:
Fie: ,
, ,
,
c=10, d=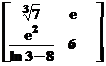 .
.
Sa se calculeze:
produsele:ab;ac;ca;cb; ad
Ex.3:
Fie : , b=
, b=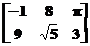 , c=10.
, c=10.
Sa se calculeze:
a:b;a:c;c:a;c:b.
Ex.4:
Fie : , b=
, b=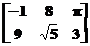 , c=10.
, c=10.
Sa se calculeze:a.b;a.c;c.a;c.b.
Ex.5:
Fie : , b=
, b=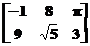 , c=10.
, c=10.
Sa se calculeze : ab;
ac; ca; cb.
Ex.6:
Sa se determine transpusa
tabloului  .
.



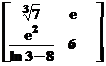 .
.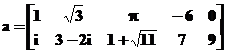 .
.



 De exemplu, pentru apelarea unui element de pe linia 2, coloana 3 si pagina 2 (schema alaturata ),
se vor folosi trei indici de acces (2,3,2).
De exemplu, pentru apelarea unui element de pe linia 2, coloana 3 si pagina 2 (schema alaturata ),
se vor folosi trei indici de acces (2,3,2).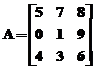 cu dimensiunea 3x3,
cu dimensiunea 3x3,



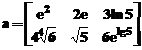 ,
,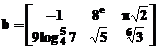 ,c=2
,c=2 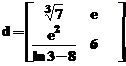
 ,
, ,
, .
.