Instrumente si tehnici
de baza ale managementului calitatii
In contextul acestui capitol, termenul instrumente
are doua semnificatii:
a.
cele care pot fi folosite atunci cand
toate datele sunt disponibile. Atunci sarcina se limiteaza la analizarea
lor pentru rezolvarea unei probleme. Instrumentele care rezulta sunt
denumite instrumente statistice.
b.
cele care pot fi folosite in
situatiile in care nu sunt disponibile toate datele necesare. Un caz
frecvent este schitarea unui nou serviciu sau a unui nou proces. In acest
caz, datele exista in mintile persoanelor implicate in schitarea
sau desfasurarea proceselor, fiind necesara o exprimare
individuala sau de grup, inteligibila pentru toti. Este vorba de
o sarcina care depaseste pura analiza. Metodele care
se folosesc sunt numite instrumente noi sau tehnici de baza ale
managementului calitatii.
1 Instrumente de baza ale managementului
calitatii
In
decada anilor '50, au inceput sa se aplice in Japonia instrumentele
statistice de control al calitatii. Progresele, in materie de
imbunatatire continua a calitatii, s-au datorat
in mare masura folosirii acestor tehnici. Profesorul Kaoru Ishikawa a
fost cel care a extins utilizarea lor in industria din tara sa, in anii
'60, creand expresia instrumente pentru
controlul calitatii.
Aceste
instrumente pot fi descrise in mod generic ca fiind "metode pentru imbunatatirea
continua si solutionarea problemelor". Ele constau in
tehnici grafice care ajuta la intelegerea proceselor muncii in
organizatii. O sinteza a acestor instrumente este prezentata in
tabelul 5.1.
Tabelul
5.1
|
INSTRUMENTUL
|
APLICATII
|
|
Liste de control
|
- Strange
date pentru a obtine o imagine clara asupra problemei.
|
|
Histograme
|
- Prezinta tiparul variatiei
datelor;
- Demonstreaza vizual comportamentul
unui proces;
- Indica rezultatul unui proces in
raport cu cerintele fixate;
|
|
Diagrama Pareto
|
- Semnaleaza
contributia diferita asupra
rezultatului total a unui ansamblu de factori;
- Acorda prioritate
oportunitatilor de imbunatatire;
|
|
Diagrama cauza-efect
|
- Ajuta
la determinarea relatiilor intre problema si posibilele
sale cauze;
- Permite solutionarea unei probleme
plecand de la simptome;
|
|
Stratificarea
|
- Clasifica datele
disponibile pe grupe avand caracteristici similare
- Izoleaza
cauza unei probleme identificand gradul de influenta
a anumitor factori;
|
|
Diagramele de dispersie
|
- Studiaza
relatia intre doua ansambluri de date;
|
|
Grafice de control
|
- Examineaza stabilitatea unui proces;
- Indica cand un proces trebuie sa
fie ajustat;
- Evalueaza
imbunatatirile unui proces;
|
|
Alte grafice
|
- Evalueaza
imbunatatirile unui proces.
|
1.1 Lista de control
Lista de control sau de
verificare este un formular cu format de tabel sau diagrama, destinat
inregistrarii datelor pentru a obtine o imagine clara asupra
problemei. Contine ansamblul de caracteristici pe care trebuie sa le
indeplineasca o instalatie, o echipa, o persoana, pentru a
se lua in consideratie faptul ca se poate realiza sarcina
atribuita. Aceste liste continand caracteristici se folosesc cu mare
eficienta in etapa controlului calitatii.
Aceasta tehnica de culegere de
date se pregateste astfel incat utilizarea sa fie
usoara si sa se interfereze cat mai putin posibil cu
activitatea celui care realizeaza registrul. Imbunatatirea
calitatii se foloseste atat in studiul simptomelor unei
probleme, cat si in investigarea cauzelor sau in culegerea datelor pentru
a verifica o ipoteza.
Pentru a aplica in mod adecvat acest
instrument, se urmaresc pasii:
1) determinarea obiectivului, care trebuie
prezentat in mod clar: se verifica distributia unui proces, defecte
si/sau erori, se estimeaza cauze.
2) definirea modului in care se va realiza
inregistrarea: cine o va face, cum si unde, daca se vor
inregistra toate datele sau se va face o demonstratie.
3) proiectarea "Listei de control" se face
astfel incat aplicarea sa fie simpla si situatia
inregistrata sa se poata intelege imediat. De asemenea,
este necesar sa se includa date ca: titlul; ce se verifica; cine
face verificarea; unde se realizeaza; metoda folosita; periodicitatea;
si, in general, orice altceva care se considera a fi necesar.
Tabelul 5.2 arata o Lista de control proiectata
pentru a investiga tipul de greseli in facturile primite intr-o mica organizatie
regionala.
Lista de control proiectata pentru a investiga tipul de greseli
in facturile primite
Tabelul 5.2
|
ZONE
|
Total
|
|
ZONA A
|
ZONA B
|
ZONA C
|
ZONA D
|
|
ERORI
|
Nu apar datele tranzactiei
|
|
|
|
|
|
|
Denumirea furnizorului
ilizibila sau inexistenta
|
|
|
|
|
|
|
S-a omis numarul de inregistrare
fiscala
al furnizorului
|
|
|
|
|
|
|
Datele firmei eronate
sau omise
|
|
|
|
|
|
|
Nu figureaza semnatura
celui care a facut cumpararea
|
|
|
|
|
|
|
Lipseste data facturii
|
|
|
|
|
|
|
Lipseste numarul facturii
|
|
|
|
|
|
|
Total
|
|
|
|
|
|
|
Perioada inregistrata : 1-3-2005/ 31-3-2005
Verificator:
Metoda: analiza facturilor primite
Periodicitate: 1/luna
|
Histogramele
O histograma este un grafic continand
linii verticale care reprezinta distributia unor date.
Constructia sa ajuta la intelegerea tendintei generale a
dispersiei si a frecventelor relative ale diferitelor valori.
Histograma este foarte utila mai ales atunci cand
este vorba despre un numar mare de date ce trebuie organizate, pentru o analiza
mai detaliata si pentru a lua decizii pe baza lor. De asemenea, este
un mijloc eficace pentru a transmite altor persoane informatii despre un proces,
intr-o forma precisa si inteligibila.
Alta aplicatie foarte interesanta
este compararea rezultatelor unui proces cu cerintele stabilite anterior
pentru aceasta. In acest caz, prin intermediul histogramei se poate vedea in ce
masura procesul produce rezultate bune si pana in ce punct
exista deviatii in privinta limitelor fixate in cerinte. In
acest sens, studiul distributiei datelor poate fi un excelent punct de
plecare pentru crearea unei ipoteze privind o functionare
nesatisfacatoare. Pentru elaborarea unei histograme de frecvente,
trebuie sa se realizeze urmatorii pasi:
1) Strangerea si inregistrarea datelor. Odata selectionata variabila
procesului ce se vrea a fi studiat, se culeg datele corespunzatoare, fiind
preferabil sa se dispuna de un numar mai mare de 50 de
observatii. In exemplul pe care il vom folosi, variabila de studiat este
timpul (in zile) necesar pentru a raspunde solicitarii unui
cetatean de a participa la un program de servicii sociale comunitare.
Au fost facute 84 de observatii pe o perioada de sase luni
(tabelul 5.3).
Timpul (in zile) necesar pentru
a raspunde solicitarii unui cetatean
Tabelul 5.3
Determinarea
rangului ansamblului de date. Rangul se obtine prin realizarea
diferentei intre valoarea maxima si valoarea minima. Rangul
trebuie sa fie un numar pozitiv.

 Exemplu:
Valoarea maxima L = 83
Exemplu:
Valoarea maxima L = 83
Valoarea minima S = 17
Precizarea
numarului de intervale si amplitudinea lor. Tabelul 5.4 ne
ajuta sa precizam numarul de intervale (k) in functie
de numarul de date disponibile. Este frecventa folosirea a zece
intervale. Pentru a calcula amplitudinea intervalelor (h), trebuie sa
impartim rangul (L - S) la numarul de intervale selectionat,
rotunjind rezultatul la intregul mai mare.
 Exemplu:
Selectionat un numar de intervale k = 10
Exemplu:
Selectionat un numar de intervale k = 10
Amplitudinea intervalului
(h) = (L - S)/K = 66/10 =6,6 = 7
Numarul de intervale in
functie de numarul de date
Tabelul 5.4
Numar de date (N)
|
Numar de intervale (k)
|
|
|
|
|
|
> 250
|
|
Determinarea
limitelor intervalelor. Aceasta va permite gruparea definitiva a
datelor. Trebuie sa tinem seama ca valorile extreme ale
fiecarui interval pot crea confuzie in privinta intervalului
caruia ii apartin. De aceea, este necesar sa se precizeze foarte
bine limitele.
In primul rand, se calculeaza punctul de
inceput al primului interval. Pentru a concretiza bine limitele, se aplica
formula:
Punctul de
inceput = Valoarea minima - Unitatea/2
 Exemplu:
Exemplu:
Se tine cont ca unitatea de
masura folosita este 1 [zi]. Plecand de aici, se insumeaza
valoarea de amplitudine a intervalului (h) pentru a obtine limitele
intervalelor urmatoare.
5) Determinarea mediei intervalelor, prin intermediul formulei:
|
Media intervalelor =
|
Limita inferioara + Limita superioara
|
|
Aceasta valoare va putea fi
utilizata pentru a calcula dispersia si tendinta centrala a
seriei de date.
Construirea tabelului de frecvente.
Se obtine inregistrand valorile limita ale intervalelor, calculand
elementele ce apartin fiecarei clase, notandu-le in coloana
"verificare" si contabilizand totalul observatiilor pentru fiecare
interval in coloana de frecvente .
Tabelul de frecvente
Tabelul 5.5
|
Numarul
|
Intervale
|
Marci de clasa
|
Verificare
|
Frecventa
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N = 84
|
Trasarea histogramei care va concentra
toata informatia acumulata pana atunci (figura 5.2).De
aceea:
axa abscisei contine: intervalele
anterior calculate;
scara verticala reprezinta
frecventele;
se traseaza bare verticale, plecand
de la fiecare interval, cu o inaltime echivalenta cu cea a
frecventei sale.
8) Interpretarea. O
histograma faciliteaza o reprezentare vizuala, in care se poate
aprecia daca masurile tind sa fie centrate sau sa se
disperseze. De asemenea, raspunde si la intrebarea daca procesul
produce rezultate bune si daca acestea apartin sau nu
cerintelor.
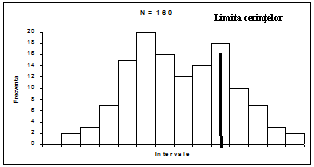
In exemplul (figura 5.2) de
referinta, se poate observa ca s-a trasat o linie aditionala:
limita cerintelor. In acest caz, cerinta programata a fost aceea ca raspunsul
sa i se dea cetateanului intr-un interval
nu mai mare de 60 de zile. Observand histograma, se vede ca un anumit numar de observatii,
la dreapta liniei, nu au indeplinit acest obiectiv. O analiza mai
detaliata ne-ar conduce la ideea ca procesul nu poseda
stabilitatea dorita. Histogramele care reflecta procese
stabile sunt mai ridicate in centru si coboara simetric spre ambele
laturi. Aici nu pare a fi indeplinita aceasta conditie, existand
o anumita asimetrie provocata de datele din afara limitei. Dar, chiar
daca datele ar fi mai stabile, putem deduce ca o parte dintre ele ar
cobori cerinta. Astfel, se pare ca in cazul nostru eforturile ar trebui
sa se indrepte spre un dublu obiectiv:
reducerea dispersiei;
deplasarea histogramei spre stanga, astfel
incat datele din extreme sa fie in cadrul limitei specificate.
Diagrama Pareto
Vilfredo Pareto, economist si sociolog
nascut in 1848, a realizat diferite studii despre distribuirea
bogatiei, observand ca 80% din aceasta se afla concentrata
la 20% din populatie.
Aceasta relatie a fost gasita si
in alte domenii. De exemplu, 80% dintre problemele unei organizatii se
datoreaza unui procent de 20% din cauzele posibile. Bineinteles
ca relatia nu este mereu exact 80/20, insa se poate afirma cu
certitudine ca un numar mic de cauze sunt responsabile de cea mai
mare parte a problemelor. Experienta a demonstrat ca cea mai mare
parte a efectelor sunt consecinta unui numar foarte mic de cauze. De
exemplu, majoritatea amenzilor in trafic se datoreaza unui numar
foarte redus de tipuri de infractiuni. Juran face aluzie la acest lucru
atunci cand vorbeste de cauze ca despre ceva de importanta
redusa. Intr-un magazin, 10% din produse pot reprezenta (forma) 90% din
cereri.
Graficul lui Pareto prezinta un interes
deosebit in circumstantele urmatoare:
identificarea cauzelor principale care provoaca
o situatie.
stabilirea importantei unei
actiuni care influenteaza asupra uneia din cauzele identificate.
evaluarea evolutiei in timp a unui
atribut determinat.
Aceasta abordare ne conduce la fenomenul putin si vital si mult si trivial, constatat de
catre J.M. Juran care, cautand o definitie a acestui fenomen, a
gasit lucrarile lui Pareto si de aceea l-a denumit Principiul
lui Pareto.
Din acest
principiu deriva diagrama lui Pareto, care constituie o metoda
grafica simpla de analiza ce permite deosebirea intre cauzele
cele mai importante ale unei probleme (putine si vitale) si cele
mai putin importante (multe si triviale). Pasii care trebuie
urmati pentru elaborarea unei diagrame Pareto sunt prezentati in continuare,
utilizand ca exemplu analiza plangerilor si reclamatiilor primite
intr-o unitate administrativa.
1. Stabilirea
datelor ce
se vor analiza si perioada de timp la care se refera datele respective.
Este necesar sa se precizeze de unde provin si cum se vor clasifica.
2.
Gruparea pe categorii. In
cazul nostru, se considera 845 de reclamatii efectuate, plecand de la
fisele de reclamatii completate de beneficiarii serviciului, care
s-au grupat in categoriile urmatoare (tabelul 5.6).
Repartizarea reclamatiilor pe categorii
Tabelul 5.6
|
CATEGORIA
|
Numar de reclamatii
|
|
Informatia transmisa
|
|
|
Orar
|
|
|
Tratamentul primit
|
|
|
Absenta formularelor
|
|
|
Timpul de solutionare
|
|
|
Prea multe formalitati
|
|
|
Pregatirea personalului
|
|
|
Asteptarea la coada
|
|
|
Altele
|
|
3.
Tabularea datelor. Se
realizeaza incepand cu acea categorie ce contine mai multe elemente
si continuand in ordine descrescatoare. Astfel se calculeaza:
frecventa absoluta;
frecventa absoluta
acumulata;
frecventa relativa unitara;
frecventa relativa
acumulata.
Tabelul 5.7
|
Nr.
crt.
|
CATEGORIA
|
Frecventa
absoluta
|
Frecventa absoluta
cumulata
|
Frecventa
relativa
unitara
|
Frecventa relativa cumulata
|
|
Timpul necesar administratiei
pentru
a raspunde
|
|
|
|
|
|
Informatia transmisa
|
|
|
|
|
|
Tratamentul primit
|
|
|
|
|
|
Prea multe formalitati
|
|
|
|
|
|
Orarul
|
|
|
|
|
|
Asteptarea la coada
|
|
|
|
|
|
Pregatirea personalului
|
|
|
|
|
|
Absenta formularelor
|
|
|
|
|
|
Altele
|
|
|
|
|
4.
Trasarea diagramei
(figura 5.3.):
a) Trasarea axelor de coordonate carteziene.
b) Pe axa ordonatelor, se delimiteaza o
scara incepand cu zero si ajungand pana la valoarea totala
a frecventei acumulate.
c) Pe axa orizontala (a abscisei) se
eticheteaza categoriile in care s-au grupat elementele, tinand cont
ca, pe o diagrama Pareto, nu exista spatiu intre bare.
d) Trasarea altei axe verticale, la dreapta
graficului, cu aceeasi lungime ca si axa din stanga, numerotata
de la 0 la 100, in care se vor reprezenta frecventele relative.
5. Reprezentarea graficului in care, pe axa orizontala, vor aparea
tot in ordine descrescatoare categoriile enumerate (figura 5.4).
6. Desenarea
curbei cumulative. Se deseneaza un punct care reprezinta totalul
fiecarei categorii. Prin unirea acestor puncte se va forma o linie poligonala
(figura 5.5).
7. Identificarea
diagramei, etichetand-o cu date ca:
titlu;
data realizarii;
perioada considerata;
procedura;
unitatea sau serviciul administrativ;
etc.
8. Analizarea
diagramei. Cu o prima aproximare, nu este greu sa se ajunga
la concluzii valide despre cauzele principale ale reclamatiilor. In
exemplu, putem observa ca aproape 2/3 dintre acestea (68%) se
datoreaza urmatoarelor doua categorii: timpul necesar administratiei
pentru a raspunde si "informatia transmisa", prima dintre
acestea fiind cea care a acumulat cele mai multe plangeri. Tinand cont
ca este mai usor sa reduci o frecventa ridicata
decat una joasa, se pare ca va fi mai util ca
imbunatatirea sa se centreze pe primele doua cauze
(putine si vitale) decat pe cele care au incidenta mai
mica (multe si triviale).
Odata indeplinite actiunile
oportune pentru reducerea acestor doua motive, se poate elabora alta
diagrama si verifica reducerea reclamatiilor la fiecare dintre
categorii.
Pe de
alta parte, diagrama Pareto poate fi aplicata pentru a afla cauzele responsabile
pentru categoriile considerate.
De exemplu, s-ar putea elabora o
diagrama de nivelul 2 pentru a determina ce aspecte produc intarzierea
unitatii administrative privind raspunsul la cereri. Atunci am
fi in fata unei faze mai concrete de analiza.
Diagrama Pareto poate avea diferite
utilizari:
sa se afle care este cauza principala a unei
probleme, separand-o de altele prezente, insa mai putin importante.
sa se decida care va fi obiectivul
actiunilor de imbunatatire, optimizand eficienta
eforturilor realizate pentru aceasta.
sa se evalueze imbunatatirile
obtinute, comparand diagrame succesive obtinute in momente diferite.
sa se investigheze efecte si cauze.
sa se comunice
usor altor membri ai organizatiei concluziile privind cauzele,
efectele si costurile erorilor.
In
sfarsit, este necesar sa mentionam ca este de mare utilitate,
in functie de caz, sa se construiasca diagrame folosindu-se
unitati financiare. Atunci e posibil ca rezultatul si semnificatia
analizei sa fie diferite.
Diagrama cauza - efect
Kaoru Ishikawa a gandit acest tip
de diagrama in anii '40 (cunoscuta si ca "Diagrama lui Ishikawa"
sau "os de peste). Diagrama lui Ishikawa este o tehnica ce ajuta
la identificarea, clasificarea si reliefarea posibilelor cauze, atat ale
unor probleme specifice cat si ale unor caracteristici ale
calitatii. Ea ilustreaza grafic relatiile existente intre
un rezultat dat (efectele) si factorii (cauzele) care
influenteaza acest rezultat.
Elaborarea unei diagrame cauza - efect trebuie sa
se ia in discutie atunci cand se doreste:
identificarea cauzelor principale ale unor
probleme sau efecte;
clasificarea si relationarea
interactiunilor intre factorii care afecteaza rezultatul unui proces;
analiza problemelor care au nevoie de
solutionare;
centrarea, intr-un grup de lucru, a
discutiei, orientand-o asupra aspectelor relevante ale unei probleme.
Pasii
care trebuie urmati pentru constructia unei diagrame cauza -
efect sunt:
1) Definirea rezultatului sau efectului care
trebuie analizat
Aceasta
definire trebuie sa fie facuta in termeni operativi, suficient
de concreti pentru a nu exista indoieli cu privire la ceea ce se
doreste, astfel incat efectul studiat sa fie inteles
satisfacator de catre membrii echipei.
Efectul
care trebuie studiat poate fi pozitiv (un obiectiv) sau negativ (o problema).Uneori,
a propune un studiu despre un efect pozitiv (un obiectiv de atins) poate
inlesni existenta unui climat care sa stimuleze participarea.
Alteori, va fi mai utila exprimarea unui efect in termenii unei probleme,
permitand axarea asupra cauzelor acesteia.
Pentru a
ilustra aceasta metoda, vom analiza apelurile telefonice
fara raspuns din partea ariilor si serviciilor unei
unitati administrative. In acest caz, avem de-a face cu perspectiva
unei probleme (efect negativ), desi ar putea fi vorba despre termeni
pozitivi (sa se raspunda la toate apelurile).
2) Situarea efectului sau a caracteristicii de
examinat. Aceasta se va pozitiona in partea dreapta a diagramei, intr-un
dreptunghi, in care trebuie sa apara cel putin o scurta
descriere a efectului.
3) Trasarea unei linii spre stanga ,
plecand de la patrat.
4) Identificarea cauzelor principale care au
legatura cu efectul
Acestea vor
fi ramurile principale ale diagramei si vor constitui categoriile sub care
se vor specifica alte posibile cauze.
Categoriile
folosite in general sunt:
3M:1P: Masini, Materiale, Metode
si Personal;
4P: Persoane , Politici, Procedee si
Bani ("plata"~ al patrulea P).
Totusi,
nu este obligatoriu sa se foloseasca aceste grupuri de categorii.
Pentru fiecare problema sau obiectiv, se vor defini cele care se
considera mai relevante in fiecare caz. Insa este convenabil ca
acestea sa nu fie mai putin de doua si mai mult de sase.
In exemplul nostru se vor folosi: Masini, Metode, Materiale si
Personal.
5) Situarea fiecareia dintre categoriile
principale ale cauzelor in patrate separate, legate de linia centrala
prin intermediul unor linii inclinate (figura 5.6).
Figura 5.6 Diagrama cauza-efect
6) Identificarea pentru fiecare ramura
principala a altor factori specifici care pot fi cauza efectului.
Acesti factori vor deservi ramurile de la nivelul al doilea. La randul
lor, acestea se vor putea extinde la altele de nivelul al treilea si
asa mai departe (figura 5.7).
Pentru
aceasta expansiune recurenta, va fi necesara folosirea unor
intrebari care sa inceapa cu "DE CE ?". De asemenea, pentru a
desprinde ramurile si diferitele niveluri, se poate folosi metoda
<<furtuna de idei>> (Brainstorming) sau "Diagrama afinitatilor".
In tabelul 5.8 se expune clasificarea factorilor
cauzali, prin metoda brainstorming, ai problemei "nu raspunde la telefon".
In coloana din stanga (cauze) ar fi situate ideile, asa cum au fost
exprimate si care servesc drept baza pentru gruparea in factori
cauzali de nivelul 3, 2 si 1. Numarul de niveluri nu este nelimitat,
astfel incat se poate intampla ca diagrama sa fie sectionata in
altele mai mici, daca apare un numar mare de niveluri pe una dintre
ramuri.
7)
Verificarea includerii factorilor. Va fi necesar sa se revada
diagrama pentru a ne asigura ca au fost inclusi in ea toti
factorii cauzali posibili.
8)
Analiza diagramei. Analiza trebuie sa ajute la identificarea cauzelor
reale. O diagrama cauza - efect identifica doar cauzele
potentiale. De aceea, va fi necesara analiza lor pertinenta
pentru a ajunge la concluzii solide privind cauzele principale ale efectului.
In aceasta faza poate fi folosita diagrama Pareto.
Anumite aspecte ale
diagramei elaborate pot sugera anumite idei:
O ramura cu un numar mare de
ramuri secundare si factori poate indica necesitatea de a realiza o
analiza mai profunda.
Daca anumite ramuri au putini
subfactori, este posibil sa se faca un efort mai mare in
identificarea cauzelor.
Daca aceeasi cauza apare in
mod repetat in diferite categorii, aceasta poate fi cauza principala.
Centralizarea datelor
rezultate din analiza diagramei cauza-efect
Tabelul 5.8
|
CAUZE
|
NIVEL 3
|
NIVEL 2
|
FACTORI
PRINCIPALI
|
Persoana de
contact ia masa
|
Mananca
|
Afara din birou
|
PERSONAL
|
|
Persoana de contact este
in alta cladire
|
In alta cladire
|
|
Persoana de contact este
intr-o sedinta de lucru
|
Sedinta de lucru
|
|
Persoana de contact are o
conversatie profesionala
|
Convorbire de serviciu
|
Linia ocupata
|
|
Persoana de contact are o
conversatie personala
|
Convorbire personala
|
|
Persoana de contact este la post
realizand munca individuala
|
Munca individuala
|
Realizarea unei alte activitati
|
|
Persoana de contact vorbeste
personal cu un beneficiar
|
Vorbeste cu un beneficiar
|
|
Persoana de contact vorbeste
cu alti membri ai organizatiei
|
Vorbeste cu un alt membru
|
|
Nu exista un protocol care
sa arate cum trebuie tratate apelurile telefonice
|
Nu exista protocol
|
Protocol
|
METODE
|
|
Exista un protocol,
insa
nu se verifica respectarea lui
|
Nu se indeplineste
protocolul
|
|
Apelul ajunge la centrala,
insa ramane in asteptare, beneficiarul intrerupand
legatura
|
Prea mult timp de asteptare
|
Directionarea apelului
|
|
Nu se primeste telefonul
in centrala
|
Telefon fara raspuns
|
|
La centrala nu se precizeaza
intinderea posibila a apelului
|
Necunoasterea extinderii
|
|
Apelul are loc in afara
programului cu publicul
|
|
In afara programului
|
|
Daca linia interna
este ocupata, nu se primeste semnal de apel
|
Linia interna ocupata
|
Infrastructura
telefonica
|
MASINI
|
|
Nu exista trecere automata
de la o linie telefonica la alta
apelata; este ocupata din exterior
|
Linia externa ocupata
|
|
Nu toate birourile dispun
de telefon
|
Distributie inadecvata
|
|
In unele servicii exista
putine aparate telefonice
|
Telefoane insuficiente
|
|
Nu se poate suna la acel telefon
|
Post neaccesibil
|
Post telefonic
|
Materiale
|
|
Postul telefonic are un nou
numar de telefon.
|
Post neactualizat
|
Avantajele
folosirii diagramei cauza - efect sunt numeroase:
ajuta la determinarea cauzelor
principale ale unei probleme sau a cauzelor caracteristicilor
calitatii, utilizand pentru aceasta o abordare organizata;
stimuleaza participarea membrilor
grupului de munca, permitand astfel sa se profite mai bine de
cunostintele pe care fiecare dintre ei le are despre proces;
stimuleaza imaginatia,
determinand formarea unor idei noi;
creste gradul de cunoastere
asupra unui proces;
identifica arii care cer un studiu
mai detaliat;
permite observarea tuturor cauzelor care
pornesc de la aceeasi situatie;
faciliteaza
comunicarea intre toate persoanele care au legatura cu problema ce se
doreste a fi rezolvata.






























Figura 5.7 Diagrama cauza-efect (telefon
fara raspuns)
Stratificarea
Este o metoda constand in clasificarea
datelor avand caracteristici similare pe grupe. Fiecarei grupe i se spune strat.
Obiectivul este acela de a izola cauza unei probleme, identificand gradul de
influenta a anumitor factori. Stratificarea se poate stabili in
functie de: personal; materiale; masini si utilaje; zonele de
gestiune; timp; mediu; localizarea geografica etc;
Stratificarea se poate baza pe diferite
instrumente ale calitatii, iar histograma este modul cel mai frecvent
de a o prezenta.
 Exemplu
Exemplu
S-au
observat intarzieri la termenul de elaborare a rezolutiilor unui serviciu
administrativ. Serviciul respectiv are doua birouri si se
doreste sa se determine daca notiunea de "birouri" poate
explica intarzierile emiterii de rezolutii.
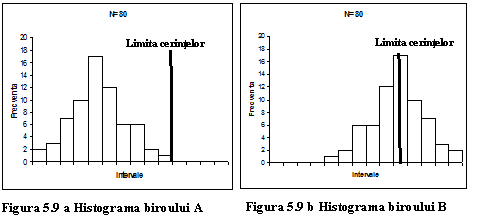
In
principiu, se elaboreaza o histograma combinata a celor
doua birouri (figura 5.8) pentru ca, ulterior, sa se realizeze
histograme pentru fiecare birou in parte (figurile 5.9 a; 5.9 b).
Se
poate observa modul in care biroul B se incadreaza aproape complet in
limita ceruta, in timp ce biroul A demonstreaza a fi responsabil
pentru deviatiile limitei fixate.
Figura 5.8 Histograma combinata a celor
doua birouri
Diagrama de dispersie
Diagrama de dispersie
Diagrama de dispersie se utilizeaza pentru a
determina daca exista vreo relatie intre doua variabile. De
exemplu, se poate intampla ca doua variabile sa fie in relatie,
astfel incat, marind valoarea uneia, sa creasca si
cealalta. In acest caz, avem o corelare pozitiva. Aceasta
corelatie poate fi puternica, atunci cand punctele de coordonate
(x,y) nu prezinta un grad mare de imprastiere; in caz contrar,
aceasta corelatie este slaba (figura 5.10 a,b). De asemenea,
s-ar putea intampla ca, atunci cand o variabila evolueaza intr-un
sens, cealalta sa derive in sens contrar; de exemplu, marind
valoarea variabilei x, sa se reduca cea a variabilei y. In acest caz
avem o corelare negativa. Aceasta corelatie este slaba,
daca punctele de coordonate (x,y) prezinta un grad mare de
imprastiere, in caz contrar corelatia este puternica (figura
5.10 c,d). In cazul in care punctele de coordonate (x, y) prezinta un grad
mare de imprastiere, intre cele doua categorii de date nu
exista corelatie. (figura 5.10, e).
Daca
unei parti dintre valorile crescatoare ale lui y ii corespunde
valori descrescatoare ale lui x, atunci se considera ca exista
o corelatie neliniara (figura 5.10 f).
Figura 5.10 Tipuri
de corelatii:
a. puternic pozitiva; b. pozitiva slaba; c.
puternic negativa;
d. negativa slaba; e. nu exista
corelatie; f. corelatie neliniara.
Pasii care trebuie parcursi pentru a
realiza o diagrama a dispersiei sunt urmatorii:
1. culegerea a mai mult de
30 de perechi de date;
2. realizarea unui sistem
de axe, astfel incat ambele axe sa aiba o lungime similara;
3. reprezentarea perechilor
de date.
 Exemplu
Exemplu
Se
doreste imbunatatirea proceselor de selectie realizate
de o organizatie. De aceea, se considera necesar a se evalua
validitatea probelor de selectie folosite. Pentru aceasta, se doreste
determinarea relatiei existenta intre punctajele obtinute de
catre un grup de candidati intr-o proba selectiva si cele
pe care toti acesti oameni le- au obtinut in evaluarea
randamentului, proba realizata un an mai tarziu de la intrarea in organizatie.
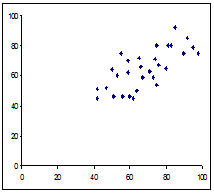
Perechile de date obtinute se reflecta in tabelul 5.9, diagrama
dispersiei corespunzatoare este prezentata in figura 5.11 in care se
poate observa o corelare pozitiva intre cele doua variabile. Gradul
acestei corelari este aratat printr-un coeficient de corelare. In prezent,
exista programe informatice (precum foile de calcul) ce permit realizarea
acestui lucru foarte usor, prin introducerea seriilor de valori. In
exemplul nostru, coeficientul de corelare pentru datele in cauza este: r =
0.71, ceea ce inseamna o corelare puternica. Coeficientul de corelare
poate avea o valoare cuprinsa intre -1 si 1. Maxima corelare
pozitiva ar fi 1, maxima corelare negativa -1; o valoare 0 ar insemna
o corelare nula intre variabile
Tabelul 5.9
Grafice de control
Graficele de control sunt instrumente statistice
folosite pentru a evalua stabilitatea unui proces. Acestea permit sa se
distinga cauzele variatiei. Orice proces poate avea variatii,
acestea putandu-se grupa in:
cauze aleatorii ale
variatiei. Sunt cauze necunoscute
si cu putina importanta, datorate intamplarii
si prezente in orice proces;
cauze specifice (imputabile sau atribuibile). In mod normal, nu
trebuie sa fie prezente in proces. Provoaca variatii importante.
Cauzele aleatorii sunt greu de identificat si
eliminat. Cauzele specifice, in schimb, pot fi descoperite si eliminate,
pentru a atinge obiectivul de stabilizare a procesului.
In afara de capacitatea de a distinge intre
cauze aleatorii si specifice, graficele de control sunt utile pentru a
supraveghea variatia unui proces in timp, pentru a proba eficienta
actiunilor de imbunatatire realizate, ca si pentru a
estima capacitatea unui proces.
Graficele de control au fost concepute de Shewhart
in timpul desfasurarii controlului statistic al
calitatii.
Au avut o mare raspandire, fiind foarte
folosite in controlul proceselor industriale. Totusi, o data cu
reformularea conceptului de calitate si extinderea sa la intreprinderi de
servicii si la unitatile administrative si auxiliare, s-au
transformat in metode de control aplicabile proceselor realizate in aceste organizatii.
Exista diferite grafice de control:
grafice
de variabile, care la randul lor pot fi:
grafice de control Xm-R (medie si
rang). Reflecta grafic dimensiuni, greutate, timp.
grafice de control X-R(mediana
si rang). Sunt similare celor anterioare, dar au o precizie mai mica.
grafice de date prin atribute. Cer recalcularea
masuratorilor discrete de genul acceptabil/inacceptabil, da/nu. Acest tip da mai putina
informatie decat cele anterioare, de aceea folosirea lui este mai
putin frecventa.
Metodologia determinarii parametrilor
statistici necesari pentru construirea diagramei de control este
prezentata in standardele ISO 7870 si ISO 8258.
Graficele de control au la baza ideea ca
variatia unei caracteristici a calitatii poate fi
cuantificata, obtinand mostre ale iesirilor dintr-un proces
si estimand parametrii distributiei sale statistice. Reprezentarea
acestor parametri intr-un grafic in functie de timp va permite constatarea
schimbarilor in distributie.
Graficul are o linie centrala si
doua limite de control : una superioara (LCS) si alta
inferioara (LCI). Spatiul dintre ambele limite defineste
variatia aleatorie a procesului. Punctele care trec de aceste doua
limite indica prezenta cauzelor specifice ale variatiei.
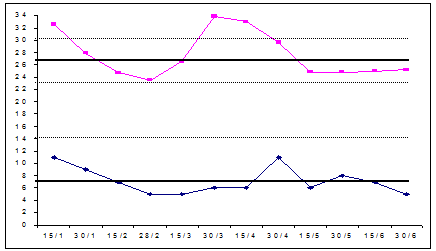
In acest paragraf se va prezenta
desfasurarea graficului prin variabile de medie si rang (x - R).
Acest grafic aduce destule informatii si este probabil cel mai
utilizat. Modul de trasare a acestui tip de grafic de control este
urmatorul:
1. Determinarea datelor ce vor trebui sa se
refere la o variabila a procesului considerata relevanta. In
exemplul nostru, datele vor corespunde "timpului de a raspunde solicitarilor
de includere in programul A de servicii sociale comunitare".
2. Strangerea de date. Mostra trebuie sa fie
constituita dintr-un numar suficient de date. Frecvent, acest
numar este peste 100, desi se poate culege un numar mai mic.
Datele stranse se grupeaza pe subgrupe ale caror dimensiuni oscileaza
intre 4 si 10 observatii. Cu cat dimensiunea subgrupurilor este mai
mare, cu atat va fi mai sensibil graficul de control. Cat despre numar, in
procesele industriale se obisnuieste a se reuni 20 sau 25, desi
este admisibil si un numar mai mic, in functie de
caracteristicile procesului studiat. Ceea ce este insa fundamental este ca
datele subgrupurilor sa se ia secvential, in diferite momente ale procesului.
In exemplul urmator, au fost luate 12 subgrupuri, care corespund
raspunsurilor emise la solicitarile cetatenilor in perioade
de 15 zile. Se poate considera fiecare perioada ca fiind un lot si
cele sase observatii ale fiecaruia dintre ele corespund
solicitarilor efectuate consecutiv.
3. Calcularea mediei pentru fiecare subgrup de
date:

4. Calcularea rangurilor sau a traseelor pentru fiecare subgrup:
R = (valoarea maxima a lui x - valoarea
minima a lui x);
5. Calcularea mediei mari (media mediilor) a
subgrupurilor:
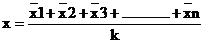 , k fiind numarul
subgrupurilor;
, k fiind numarul
subgrupurilor;
6. Calcularea mediei rangurilor subgrupurilor: