ELEMENTE DE ALGEBRA LINIARA
Transpusa unei matrice 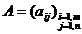 cu
cu 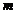 linii si
linii si 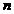 coloane este o matrice
notata
coloane este o matrice
notata  cu
cu 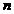 linii si
linii si 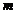 coloane, unde
coloane, unde 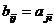 ,
,  .
.
Determinantul matrice de ordinul 2  ,este
,este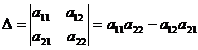
Determinantul matrice de ordinul 3 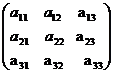 ,este
,este 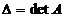 , unde:
, unde:
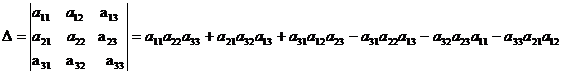 .
.
Regula minorilor(dezvoltarea determinantului dupa o linie sau
coloana)
Alegem o linie sau o coloana si inmultim fiecare element 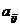 al acestei linii sau
coloane cu determinantul de ordin inferior obtinut prin eliminarea liniei
al acestei linii sau
coloane cu determinantul de ordin inferior obtinut prin eliminarea liniei 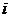 si a coloanei
si a coloanei  si cu
si cu 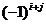 ; adunam produsele astfel obtinute si
obtinem valoarea determinantului.
; adunam produsele astfel obtinute si
obtinem valoarea determinantului.
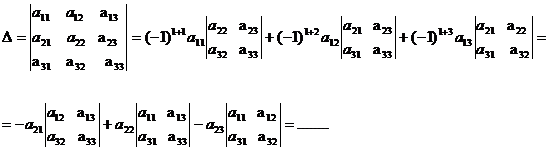
Proprietati ale determinantilor:
Determinantul
unei matrice patratice este egal cu determinantul matricei transpuse
O matrice care
are o linie (sau o coloana) cu toate elementele 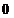 , are determinantul
, are determinantul 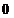
Daca
inmultim toate elementele unei linii (sau unei coloane) dintr-o matrice cu
un numar, valoarea determinantului matricei se inmulteste cu
acel numar.
Daca intr-o
matrice adunam toate elementele unei linii (sau unei coloane) cu
elementele corespunzatoare unei alte linii (sau unei alte coloane),
inmultit cu un numar, valoarea determinantului nu se schimba.
Daca o
matrice are doua linii (respectiv doua coloane) proportionale,
atunci determinantul este nul.
Daca
schimbam intre ele doua linii (sau doua coloane) dintr-o matrice
patratica atunci valoarea determinantului se inmulteste cu 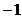 .
.
Daca
matricele 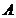 si
si 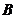 difera printr-o
singura linie
difera printr-o
singura linie 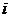 , atunci determinantul matricei care are pe linia
, atunci determinantul matricei care are pe linia 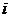 suma celor doua
linii
suma celor doua
linii 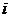 din matricele
din matricele 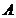 si
si 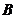 este egal cu suma
este egal cu suma 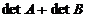 .(acelasi enunt respectiv pentru coloane)
.(acelasi enunt respectiv pentru coloane)
Determinantul
produsului a doua matrice patratice de acelasi ordin este egal
cu produsul determinantilor celor doua matrice.
Daca o
linie (respectiv coloana) a determinantului unei matrice este o
combinatie liniara a celorlalte linii (respectiv coloane) ale
aceluiasi determinant, atunci determinantul este nul.
Valoarea 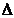 a determinantului matricei
asociate unui sistem determina compatibilitatea sistemului (existenta
solutiilor): daca
a determinantului matricei
asociate unui sistem determina compatibilitatea sistemului (existenta
solutiilor): daca 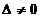 ,sistemul este compatibil determinat (sistemul are o
solutie unica); daca
,sistemul este compatibil determinat (sistemul are o
solutie unica); daca  , atunci sistemul poate fi incompatibil (nu are solutii) sau compatibil nedeterminat(are o
infinitate de solutii).
, atunci sistemul poate fi incompatibil (nu are solutii) sau compatibil nedeterminat(are o
infinitate de solutii).
Metoda lui Cramer
Fie § u sistem liniar cu necunoscutele 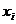 si
si 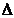 determinantul
sau. Presupunem ca
determinantul
sau. Presupunem ca 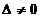 .Notam cu
.Notam cu 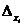 determinantul
obtinut prin inlocuirea coloanei corespunzatoare necunoscutei
determinantul
obtinut prin inlocuirea coloanei corespunzatoare necunoscutei 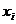 cu coloana termenilor
liberi.
cu coloana termenilor
liberi.
Solutia sistemului liniar 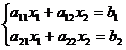 , este
, este 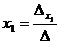 si
si 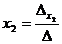 .
.
Solutia sistemului liniar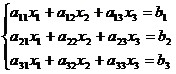 , este
, este
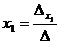 ,.
,.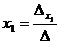 si
si  .
.
Solutia sistemului liniar , este
, este
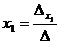 ,.
,.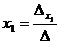 ,
, si
si 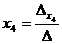 .
.
Un sistem liniar omogen are toti
determinantii 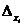 nuli, deci admite
intotdeauna cel putin solutia nula
nuli, deci admite
intotdeauna cel putin solutia nula 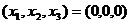 . Acest sistem admite si solutii nenule daca
. Acest sistem admite si solutii nenule daca  .
.
Fie  o matrice
patratica de ordin
o matrice
patratica de ordin 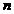 cu coeficienti in
cu coeficienti in
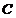 .
.
Matricea 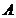 este inversabila
daca si numai daca
este inversabila
daca si numai daca 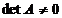 .
.
Matricea inversa a matricei 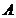 este
este 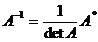 , unde
, unde 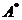 se obtine inlocuind fiecare element al
matricei transpuse
se obtine inlocuind fiecare element al
matricei transpuse 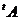 cu complementul
sau algebric
cu complementul
sau algebric 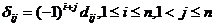 , unde
, unde 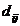 este minorul
elementului
este minorul
elementului 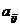 din
din 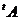 . (determinantul obtinut din
. (determinantul obtinut din 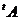 prin eliminarea liniei
prin eliminarea liniei
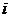 si coloanei
si coloanei  ).
).
Ecuatii
matriceale
Sistemul liniar poate fi exprimat matriceal astfel: , unde
, unde 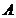 este matricea
coeficientilor necunoscutelor,
este matricea
coeficientilor necunoscutelor, 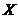 este matricea
necunoscutelor
este matricea
necunoscutelor
(matrice coloana) si 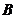 este matricea
termenilor liberi (matrice coloana).Daca matricea
este matricea
termenilor liberi (matrice coloana).Daca matricea 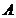 este inversabila
avem:
este inversabila
avem: 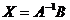 .
.
Daca matricea 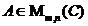 nu este nula,
exista un numar natural
nu este nula,
exista un numar natural  , astfel incat cel putin un minor de ordinul
, astfel incat cel putin un minor de ordinul  (format la
intersectia a
(format la
intersectia a  linii si
linii si  coloane din matrice)
este nenul, iar toti determinantii de ordin mai mare decat
coloane din matrice)
este nenul, iar toti determinantii de ordin mai mare decat  (daca exista) sunt nuli.
(daca exista) sunt nuli.
Acest numar  se numeste rangul
matricei.
se numeste rangul
matricei.
Rangul unei matrice ramane neschimbat
daca :
- Multiplul unei linii (coloane) se aduna la
o alta linie (coloana);
- Liniile (coloanele) se schimba intre ele.
TEOREMA KRONECHER-CAPELLI
Un sistem de ecuatii liniare este compatibil
daca si numai daca rangul matricei sistemului este egal cu
rangul matricei extinse, formata din matricea sistemului la care se
adauga coloana termenilor liberi.
TEOREMA LUI ROUCHE
Un sistem de ecuatii liniare este compatibil
daca si numai daca toti determinantii caracteristici
sunt nuli. Determinantii caracteristici se3 obtin adaugand o
linie si o coloana din matricea extinsa unui minor cu
determinantul nenul.


 ,este
,este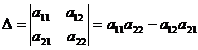
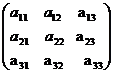 ,este
,este 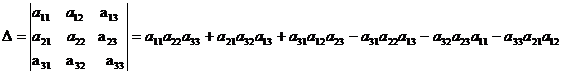 .
.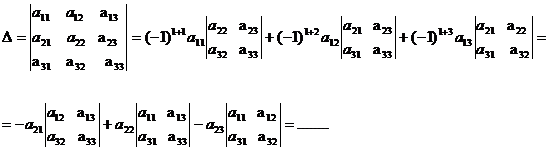
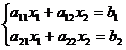 , este
, este 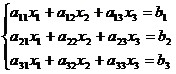 , este
, este  , este
, este