Ecuatii cu nucleu compact
Vom studia ecuatia de forma :
x
─ λU(x) =y (*
unde U este
un operator liniar continuu, care aplica spatiul Banach X in el
insusi. O astfel de ecuatie va fi numita ecuatie de speta a doua, iar operatorul U - nucleul ecuatiei. Aceasta
terminologie este imprumutata din teoria ecuatiilor integrale, unde
se numeste ecuatie de speta a doua ecuatia
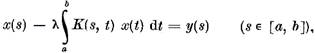
spre deosebire de ecuatia de speta intai
:
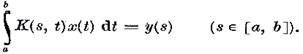
Desi formal, ecuatia
functionala (*) poate fi scrisa si sub forma unei
ecuatii "de speta intai"
T (x) = y (T=I-λU),
totusi separarea operatorului identitate se
dovedeste a fi indicata, intrucat operatorul U poate avea
proprietatile mai bune decat operatorul T, care sa permita
sa se studieze mai complet ecuatia (*)
Consideram :
x ─ U(x) =y (x, y є X)
si adjuncta ei
g ─ U*(g f (f, g є X*)
presupunand ca U (prin urmare si U*)
sunt operatori compacti in spatiul Banach X. Notam T = I ─
U, unde, prin I s-a notat
operatorul identitate in spatiul X. Cu aceasta notatie
ecuatia (1) poate fi scrisa mai scurt :
T(x = y
Iar ecuatia (2) :
T*(g f
Intrucat T*
= I* ─ U* si I*este
operatorul identitate in X*.
I.1 Proprietati ale operatorului T
Vom
demonstra in prealabil trei leme.
Lema I.1.1 Multimea T (X) este inchisa.
Demonstratie Sa notam
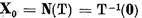
si sa consideram spatiul cat

si operatorul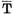 care aplica
care aplica 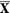 in
in 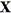 .Vom nota prin
φ omomorfismul natural al spatiului X pe
.Vom nota prin
φ omomorfismul natural al spatiului X pe 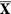 . Fie
. Fie 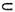 T(X) un sir convergent catre un element
T(X) un sir convergent catre un element 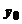 X. Deoarece
X. Deoarece  exista elementele
exista elementele
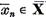 astfel ca
astfel ca  Din definitia normei in spatiul cat
exista
Din definitia normei in spatiul cat
exista 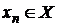 astfel incat
astfel incat

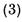
Vom demonstra ca sirul 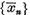 este marginit.
In caz contrar, trecand, daca este necesar, la un subsir, putem
presupune ca
este marginit.
In caz contrar, trecand, daca este necesar, la un subsir, putem
presupune ca 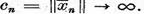 In virtutea
relatiei (3),sirul
In virtutea
relatiei (3),sirul 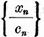 este marginit, de aceea, trecand inca o data la
este marginit, de aceea, trecand inca o data la
un subsir, putem considera
ca 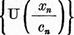 converge. Fie, de exemplu,
converge. Fie, de exemplu,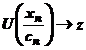 Avand in vedere ca
Avand in vedere ca  T(xn) = T (xn) =y
T(xn) = T (xn) =y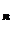 putem scrie
putem scrie

si prin urmare,
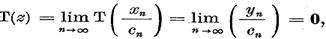
deci z є
Xo. Dar atunci
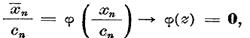
ceea ce este
imposibil, intrucat 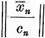 = 1 pentru orice n=1,2, . .
= 1 pentru orice n=1,2, . .
Astfel, sirul 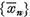 si conform relatiei (3), si
sirul
si conform relatiei (3), si
sirul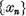 este marginit. Putem ,de aceea considera
ca este un sir convergent. Daca, de exemplu, U (
este marginit. Putem ,de aceea considera
ca este un sir convergent. Daca, de exemplu, U (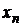 )
) x atunci
x atunci
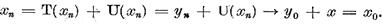
Deci obtinem
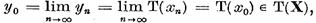
ceea ce trebuia demonstrat.
Lema I.1.2. Sirul de multimi

este crescator si contine
doar un numar finit de multimi distincte.
Demonstratie. Prima parte a
afirmatiei lemei este aproape evidenta, deoarece, daca 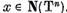 atunci
atunci 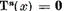 si cu atat mai mult
si cu atat mai mult 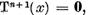 adica
adica
x 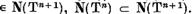
Pentru demonstrarea celei de-a doua parti, vom nota 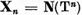 si vom stabili ca, daca, pentru
un n=1,2, . ,Xn = Xn atunci si
si vom stabili ca, daca, pentru
un n=1,2, . ,Xn = Xn atunci si 
Sa alegem 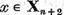 . Aceasta
inseamna ca
. Aceasta
inseamna ca 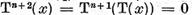
si, prin
urmare,T(x)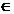 X
X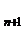 =X
=X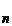 .Dar atunci T
.Dar atunci T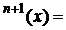 T
T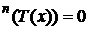 , adica x є Xn+1. Astfel
, adica x є Xn+1. Astfel 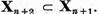 Deoarece incluziunea opusa are loc
intotdeauna, avem, in definitiv, ca
Deoarece incluziunea opusa are loc
intotdeauna, avem, in definitiv, ca 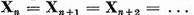
Sa
presupunem acum ca pentru fiecare n = 1,2, .
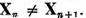
Fiecare Xn este subspatiu al spatiului Xn de aceea,
conform lemei cvasiperpendiculare, in Xn poate fi ales un
element normat  astfel ca
astfel ca
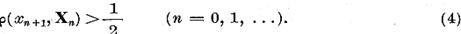
Fie m n. Sa
consideram elementul
n. Sa
consideram elementul
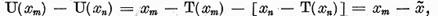 unde am notat
unde am notat 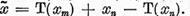 Vom demonstra ca
Vom demonstra ca 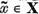 m . In acest scop,
m . In acest scop,
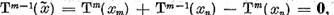
Deoarece 
Tinand
seama de inegalitatea (4), avem
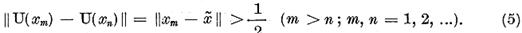
Pe de alta parte 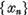 este un sir marginit, deci
datorita compacitatii operatorului U din sirul
este un sir marginit, deci
datorita compacitatii operatorului U din sirul 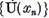 se poate extrage un subsir convergent,
ceea ce contrazice (5)
se poate extrage un subsir convergent,
ceea ce contrazice (5)
Lema I.1.3. Printre multimile
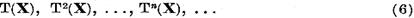
exista doar un numar finit de multimi distincte.
Demonstratia este asemanatoare in linii
generale cu demonstratia lemei precedente si ca urmare o vom da
fara a intra in amanunte.
Sa
observam ca multimile (6) sunt inchise conform lemei I.1.1
si in afara de aceasta, formeaza un sir descrescator.
Este clar ca din egalitatea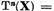
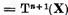 pentru un n, rezulta ca
pentru un n, rezulta ca
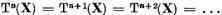
Si lema
este, in acest caz, demonstrata.
Admitand ca  vom construi cu ajutorul lemei
cvasiperpendiculare un sir
vom construi cu ajutorul lemei
cvasiperpendiculare un sir 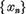 astfel incat
astfel incat
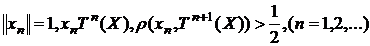 (7)
(7)
Fie m n. Ca si in
lema I.1.2, avem
n. Ca si in
lema I.1.2, avem
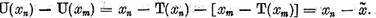
Dar
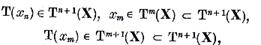
Si astfel
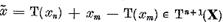 . Din (7) rezulta atunci
. Din (7) rezulta atunci
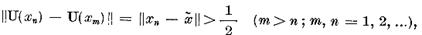
care contrazice
compacitatea operatorului U
I.2. Teorema de caracterizare a operatorului T
Sa
notam r cel mai mic dintre
numerele intregi nenegative n pentru care
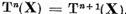 . Daca, in
particular,
. Daca, in
particular, 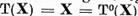 , punem r = 0
, punem r = 0
Fie apoi
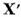
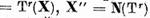 .
.
Urmatoarea
teorema contine o caracterizare a operatorului T si prin urmare,
a ecuatiei (1).
Teorema I.2.1.
a) Operatorul
T aplica injectiv subspatiul X' pe el insusi.
b)
Subspatiul 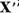 este finit dimensional. Operatorul T
aplica
este finit dimensional. Operatorul T
aplica 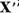 in el insusi.
in el insusi.
c)Fiecare
element x є X poate fi reprezentat in mod unic sub forma
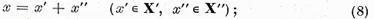
pe
langa aceasta, exista o constanta M  0 astfel incat
0 astfel incat
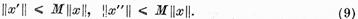
d)
Operatorul U admite reprezentarea

unde
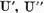 sunt operatori compacti, care aplica
spatiul X in X' operatorul
sunt operatori compacti, care aplica
spatiul X in X' operatorul 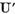 ) si in
) si in 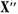 (operatorul
(operatorul 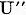 ). In plus
operatorul
). In plus
operatorul 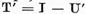 are invers bilateral continuu si este
valabila relatia
are invers bilateral continuu si este
valabila relatia

Demonstratie. a) Deoarece 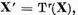

Daca
T(x)=0, unde 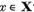 atunci, alegand conform lemei I.1.2
atunci, alegand conform lemei I.1.2 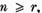 astfel ca
astfel ca 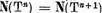 , vom avea
, vom avea  si prin urmare exista
si prin urmare exista 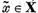 astfel ca
astfel ca 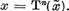 Dar atunci
Dar atunci  si de aceea
si de aceea 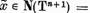
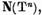 de unde avem
de unde avem 
b)Avem
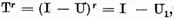
unde operatorul U este o combinatie liniara de puteri pozitive
ale operatorului U.
Astfel operatorul U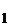 este compact. Deoarece pentru
este compact. Deoarece pentru 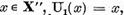 rezulta ca orice multime
marginita din
rezulta ca orice multime
marginita din 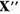 este relativ compacta.
este relativ compacta. 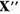 este
finit-dimensional.
este
finit-dimensional.
Multimea 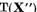 in cazul
in cazul 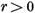 este evident
este evident 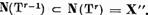 Daca
Daca 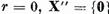 si incluziunea
si incluziunea 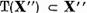 este
triviala.
este
triviala.
c) Sa
notam 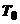 operatorul T considerat doar
pe multimea
operatorul T considerat doar
pe multimea  . Pe baza lemei I.1.1
aplicata operatorului
. Pe baza lemei I.1.1
aplicata operatorului 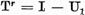 tragem concluzia ca multimea
tragem concluzia ca multimea 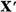 este inchisa si prin urmare este spatiul Banach.De aici operatorul T care aplica injectiv X' pe el
insusi are invers continuu
este inchisa si prin urmare este spatiul Banach.De aici operatorul T care aplica injectiv X' pe el
insusi are invers continuu 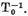
Fie x un
element arbitrar din X, sa
punem
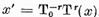
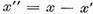
 (12)
(12)
Este clar ca x' є X' si deoarece
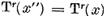 ─
─ 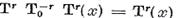 ─
─ 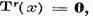
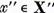 ceea ce demonstreaza posibilitatea
reprezentarii lui x sub
forma (8). Daca
ceea ce demonstreaza posibilitatea
reprezentarii lui x sub
forma (8). Daca 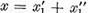 este o alta reprezentare a elementului x in forma (8) deci astfel incat
este o alta reprezentare a elementului x in forma (8) deci astfel incat 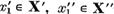 atunci
atunci
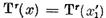 +
+
Dar deoarece 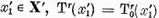 si de aceea
si de aceea
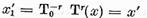
Si unicitatea reprezentarii (8) este
demonstrata.
Existenta estimarilor (9)rezulta pe
baza relatiilor (12) din continuitatea operatorului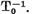
d) Avand in vedere ca U=I ─ T avem pentru 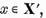
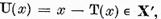
deci operatorul U aplica 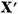 in el insusi. Analog ne convingem ca
in el insusi. Analog ne convingem ca
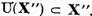
Sa punem pentru 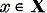 arbitrar
arbitrar
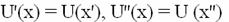 (13)
(13)
Unde  si
si 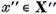 sunt cei din reprezentarea elementului x in forma (8). Tinand seama de
estimarile (9) ne convingem fara dificultate ca
sunt cei din reprezentarea elementului x in forma (8). Tinand seama de
estimarile (9) ne convingem fara dificultate ca 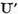 si
si 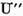 sunt operatori liniari continui. In afara
de aceasta este clar ca
sunt operatori liniari continui. In afara
de aceasta este clar ca 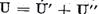 si
si 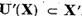 ,
, 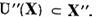 Mai departe este
evident ca
Mai departe este
evident ca

Din aceste relatii rezulta ca 
Operatorul 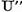 aplica spatiul X in spatiul
finit-dimensional in care fiecare multime marginita este relativ
compacta. De aceea U
aplica spatiul X in spatiul
finit-dimensional in care fiecare multime marginita este relativ
compacta. De aceea U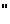 este operator compact. Din U
este operator compact. Din U =U-U
=U-U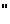 se poate trage concluzia ca operatorul U
se poate trage concluzia ca operatorul U este compact.
este compact.
Sa demonstram , in sfarsit, ca
operatorul 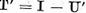 are invers bilateral continuu. Pentru aceasta
este suficient sa stabilim in primul rand ca
are invers bilateral continuu. Pentru aceasta
este suficient sa stabilim in primul rand ca 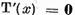 implica x = 0 si in al doilea rand ca
implica x = 0 si in al doilea rand ca 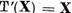 . Fie
. Fie 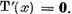 Reprezentand x sub forma (8) obtinem ca
Reprezentand x sub forma (8) obtinem ca
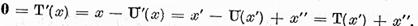
Deoarece 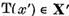 vom avea ca urmare a unicitatii
reprezentarii elementului 0 sub forma (8),
vom avea ca urmare a unicitatii
reprezentarii elementului 0 sub forma (8),
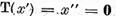
si pe baza punctului a), 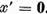 . De aici
. De aici 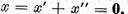
Sa consideram acum un element arbitrar 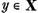 . Sa-l
reprezentam sub forma
. Sa-l
reprezentam sub forma
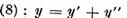
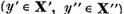 si sa punem
si sa punem
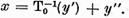
Deoarece 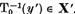

Si
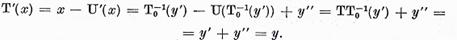
Asadar 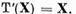
Teorema este in intregime demonstrata.
Observatie. Fie
m cel mai mic dintre numerele intregi nenegative n astfel ca 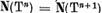 . Atunci m = r.
. Atunci m = r.
In acest scop luand 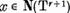 si reprezentandu-l sub forma (8)
obtinem
si reprezentandu-l sub forma (8)
obtinem
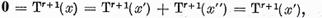
ceea ce este posibil in virtutea punctului a) doar
pentru  De aici
De aici 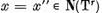 si prin urmare
si prin urmare  .
.
Mai departe , daca  , atunci punand x in forma (8) vom avea
, atunci punand x in forma (8) vom avea
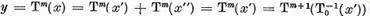
si 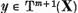 prin urmare de asemenea
prin urmare de asemenea 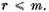 .
.
Teorema urmatoare este consecinta unui
caz particular al acestei observatii.
Teorema I.2.2. Pentru ca ecuatia (1) sa
aiba solutie pentru orice y є X este necesar si suficient
ca ecuatia omogena
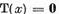 (15)
(15)
sa
aiba solutie unica (evident x
Intr-adevar rezolubilitatea ecuatiei (1)
pentru orice y є X
inseamna ca 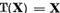 astfel spus ca r = 0. Unicitatea
solutiei ecuatiei (15) este echivalenta cu faptul ca m = 0.
astfel spus ca r = 0. Unicitatea
solutiei ecuatiei (15) este echivalenta cu faptul ca m = 0.
I.3.Legatura
ecuatiei cu adjuncta ei
In teorema urmatoare se stabileste o
legatura intre ecuatiile (1) si (2).
Teorema I.3.1 Multimile N(T) si N(T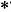 ) au aceeasi dimensiune finita.
) au aceeasi dimensiune finita.
Demonstratie. Deoarece 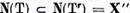 si pe baza punctului b)al teoremei I.2.1,
si pe baza punctului b)al teoremei I.2.1,
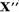 este finit - dimensional, rezulta ca
N(T) va fi finit - dimensional. Intrucat U
este finit - dimensional, rezulta ca
N(T) va fi finit - dimensional. Intrucat U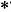 este tot
operator compact, cele spuse sunt aplicabile si multimii N(T
este tot
operator compact, cele spuse sunt aplicabile si multimii N(T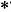 )
)
Fie
n dimensiunea lui N(T) si m dimensiunea lui N(T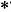 ). Fie
). Fie 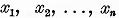 un sistem de elemente liniar independente din
N(T) si
un sistem de elemente liniar independente din
N(T) si  elementele liniar independente din N(T
elementele liniar independente din N(T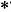 )
)
Intrucat elementele 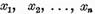 sunt liniar independente exista un sistem
biortogonal de functionale
sunt liniar independente exista un sistem
biortogonal de functionale 
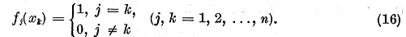
Analog exista elementele 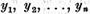 astfel ca
astfel ca
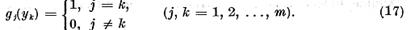
Sa presupunem ca 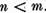 . Sa
consideram in spatiul X operatorul V=U+W unde
. Sa
consideram in spatiul X operatorul V=U+W unde
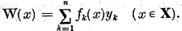
Deoarece operatorul liniar W aplica X intr-un
spatiu finit - dimensional el este compact. Inseamna ca si
V este operator compact. Sa consideram ecuatia
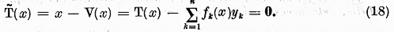
Fie 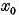 o solutie a sa :
o solutie a sa :
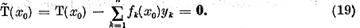
Din aceasta egalitate rezulta ca
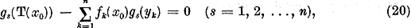
adica tinand seama de relatiile (17)
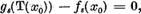
si prin urmare a faptului ca 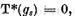 vom avea
vom avea
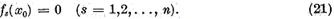
Impreuna cu (19) aceasta da 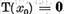 , adica
, adica  si deci
si deci 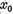 poate fi
reprezentat sub forma
poate fi
reprezentat sub forma
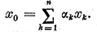
Deoarece in virtutea relatiilor (16) 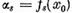 din (21) rezulta ca
din (21) rezulta ca 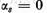 si de aceea si
si de aceea si  . Astfel
ecuatia (18)are solutie unica. Conform teoremei I.2.2
ecuatia neomogena corespunzatoare este rezolubila pentru
orice membru drept. In particular ecuatia
. Astfel
ecuatia (18)are solutie unica. Conform teoremei I.2.2
ecuatia neomogena corespunzatoare este rezolubila pentru
orice membru drept. In particular ecuatia
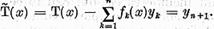
are solutie. Sa notam 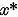 solutia acestei ecuatii. Pe de o
parte ,
solutia acestei ecuatii. Pe de o
parte ,
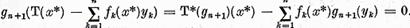
Insa pe de alta parte 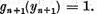
Astfel trebuie ca 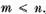
Posibilitatea inegalitatii  se exclude prin rationamente analoage.
Anume, in locul ecuatiei (18) trebuie considerata in spatiul
se exclude prin rationamente analoage.
Anume, in locul ecuatiei (18) trebuie considerata in spatiul 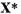 ecuatia
ecuatia
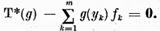
I.4.Alternativa
Fredholm
Reunind
teoremele demonstrate mai sus, obtinem urmatorul rezultat.
Teorema I.4.1. Fie ecuatiile (1) si (2)
au solutii pentru orice membru drept si atunci solutiile lor
sunt unice; fie ecuatiile omogene
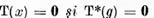
au acelasi numar finit de solutii liniar independente 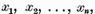 respectiv
respectiv 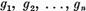 . In acest ultim
caz pentru ca ecuatia (1) (respectiv ecuatia (2)sa aiba
solutie , este necesar si suficient ca
. In acest ultim
caz pentru ca ecuatia (1) (respectiv ecuatia (2)sa aiba
solutie , este necesar si suficient ca
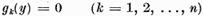
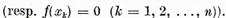
iar solutia generala a ecuatiei (1)
are forma :
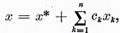
iar solutia generala a ecuatiei
(2):
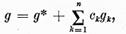
unde 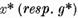 este o solutie oarecare a
ecuatiei(1) (respectiv2) iar
este o solutie oarecare a
ecuatiei(1) (respectiv2) iar 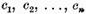 sunt constatate arbitrare.
sunt constatate arbitrare.
Avand in vedere analogia cu teorema cunoscuta
din teoria ecuatiilor integrale , teorema de fata se numeste alternativa lui Fredholm


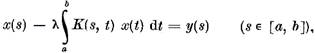
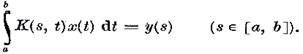
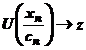 Avand in vedere ca
Avand in vedere ca