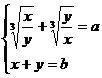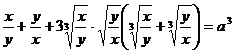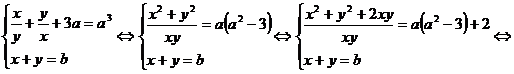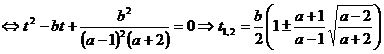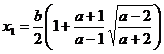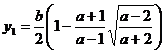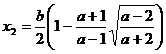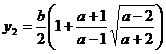Sisteme de
ecuatii de gradul I si II
TIPUL 1: Se da sistemul:
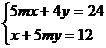 ;
; 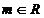
a)
Sa se rezolve si sa discute sistemul dupa
valorile parametrului real m.
b) Sa se
determine valorile intregi ale parametrului m
astfel ca sistemul sa admita ca solutii numere intregi.
Rezolvare:
a) Reducand pe "y" se obtine:
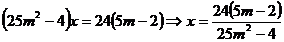 ,
, 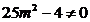
Reducand pe "a" se obtine
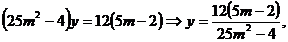
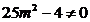
Pentru 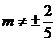 sistemul este
compatibil determinat cu solutia:
sistemul este
compatibil determinat cu solutia:
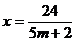 ,
, 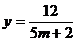
Pentru 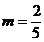 sistemul se reduce la:
sistemul se reduce la:
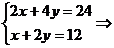 nedeterminat, cu solutia
nedeterminat, cu solutia 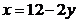 si
si 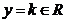
Pentru 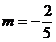 sistemul devine:
sistemul devine:
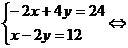
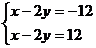
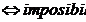
b)
Trebuie sa avem
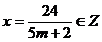 ;
; 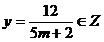
Adica "5m + 2" este un ivisor al
numarului 12. Multimea divizorilor lui 12 este: 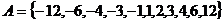 , din conditiile
, din conditiile 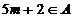
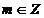
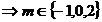
Deci:
|
m = -1
|
|
x = -8
|
|
y = -4
|
|
m = 0
|
|
x = 12
|
|
y = 6
|
|
m = 2
|
|
x = 2
|
|
y = 1
|
TIPUL 2: Sa se discute sistemul:
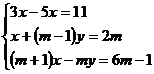
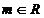
Rezolvare:
Din primele 2 ecuatii se obtine:
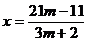
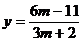
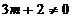
Sistemul este compatibi daca aceste valori pentru
"x" si "y" verifica ecuatia a treia.
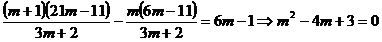
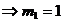
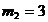
Cazuri:
a) m =
1 - sistemul este compatibil: x = 2, y = -1
b) m =
3 - sistemul este compatibil: 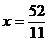
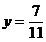
c) 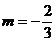 - sistemul se scrie:
- sistemul se scrie: 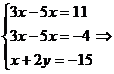 incompatibil
incompatibil
d)
m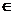 R - sistemul este incompatibil.
R - sistemul este incompatibil.
TIPUL 3: Se da sistemul
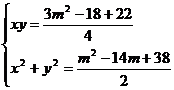
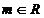
a)
Sa se rezolve sistemul.
b)
Sa se afle valorile parametrului "m" pentru care
sistemul admite radacini reale.
Rezolvare
a) Se
inmulteste ecuatia a doua cu 2 si se aduna la prima ecuatie se obtin urmatoarele sisteme echivalente cu
sistemul dat
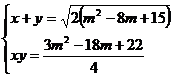
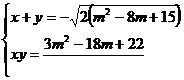
Se scriu ecuatiile de gradul al doilea
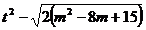
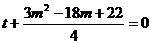
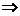
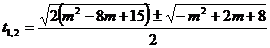
si
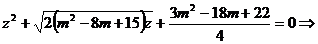
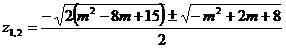
Solutiile
sistemului sunt
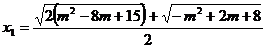
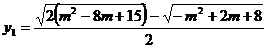
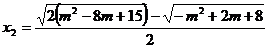
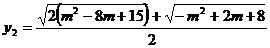
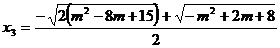
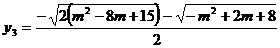
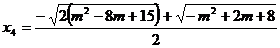
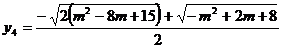
b) Solutiile
sistemului suntreale daca "m" satisface
simultan inecutiile
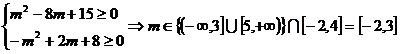
TIPUL
4: Sa se rozelve sistemul:
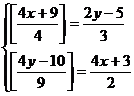
Rezolvare:
Se noteaza 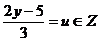 ,
, 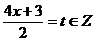
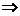
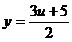 ,
, 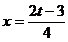
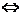
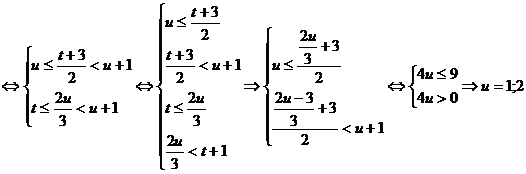
Pentru 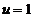 ,
, 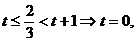
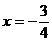 ,
, 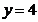 ,
,
Pentru 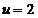 ,
, 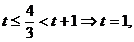
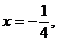
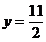 .
.
Solutiile
sistemului sunt:
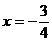

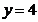
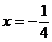
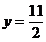
TIPUL
5:
Sa se
determine valorile reale ale lui "a" pentru care sistemul:

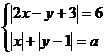
Rezolvare:
Din ecuatia nr.2 rezulta: a
≥ 0
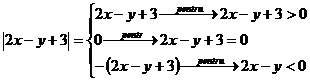
Cazul nr. 1:
Pentru 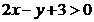 sistemul devine:
sistemul devine:
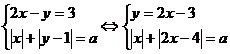
a) 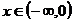 :
: 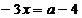 ,
, 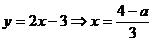 ,
, 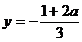
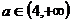
b) 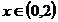 :
: 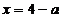 ;
; 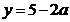 ;
; 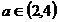
c) 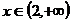 :
: 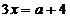 ;
; 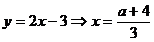 ;
; 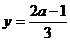 ;
; 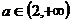
d) 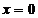 ;
; 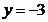 ;
; 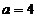
e) 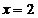 ,
, 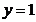 ,
, 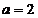
Cazul nr. 2:
Pentru 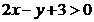 sistemul se scrie:
sistemul se scrie:
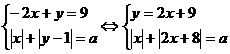
a) 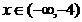 :
: 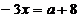 ,
, 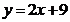
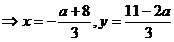
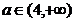
b) 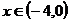 :
: 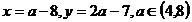
c) 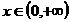 :
: 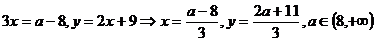
d) 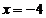 ,
, 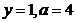
e) 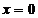 ,
, 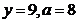
Cazul nr. 3:
Pentru 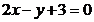 sistemul este
imposibil
sistemul este
imposibil 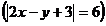
TIPUL 6 Sa se rezolve, in 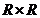 , sistemul
, sistemul
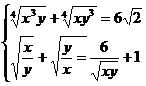
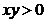 daca
daca 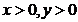 sau
sau 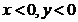 .Pentru
.Pentru 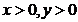 se obtine
sistemul
se obtine
sistemul
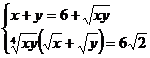
Notam 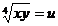
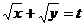 se obtine
se obtine
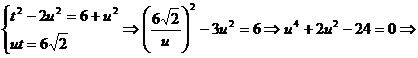
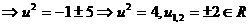 si
si 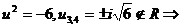
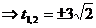 si deci
si deci 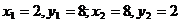
Pentru 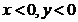 are loc sistemul
are loc sistemul
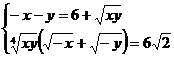
Notam 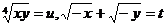 se obtine
se obtine
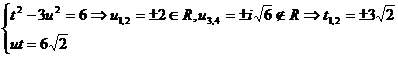
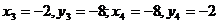

EXEMPLE
Sa se rezolve si sa se discute sistemul
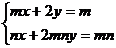
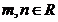
Inmultim
prima ecuatie cu "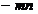 "se reduce
"se reduce 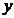
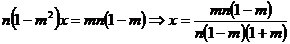
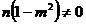
Analog
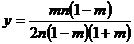
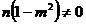
Cazul nr 1
Pentru 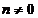 si
si 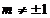 sistemul este
compatibil cu solutia
sistemul este
compatibil cu solutia
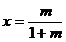
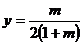
Cazul nr 2
Pentru 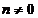 si
si 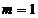 sistemul se scrie
sistemul se scrie
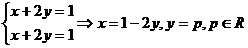 (nedeterminat)
(nedeterminat)
Cazul nr 3
Pentru 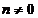 si
si 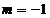 s obtine sistemul
s obtine sistemul
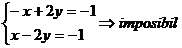
Cazul nr 4
Pentru 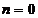 si
si 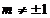 sistemul se reduce3 la
ecuatia
sistemul se reduce3 la
ecuatia 
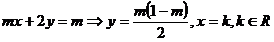 (nedeterminat)
(nedeterminat)
Cazul nr 5
Pentru 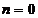 si
si 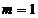 sau
sau 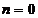 si
si 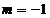 sistemul este
nedeterminat
sistemul este
nedeterminat
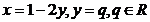 , pentru
, pentru 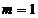 si
si 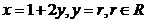 pentru
pentru 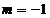
Sa se discute sistemul
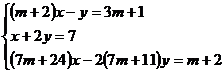
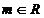
Din primele doua
ecuatii se obtine
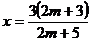
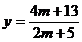
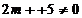
Inlocuim aceste
valori pentru 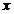 si
si 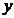 in ecuatia a
treia
in ecuatia a
treia
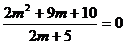
Unde 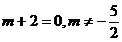
Cazul nr 1
Pentru 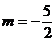 sistemul se scrie
sistemul se scrie
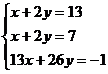 (incompatibil)
(incompatibil)
Cazul nr 2
Pentru 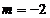 sistemul este
compatibil:
sistemul este
compatibil: 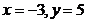
Cazul
nr 3:
Pentru 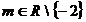 sistemul este
incompatibil
sistemul este
incompatibil
Se considera sistemul
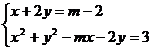
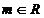
a)
Sa se rezolve sistemul
b)
Sa se determine valorile parametrului 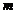 pentru care sistemul
admite numai solutii cu numere intrgi negative
pentru care sistemul
admite numai solutii cu numere intrgi negative
c)
Sa se determine valorile parametrului 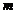 pentru care sistemul
admite o solutie
pentru care sistemul
admite o solutie 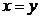
a)Inlocuim 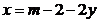 din prima ecuatie
in a doua si se obtine o ecuatie de gradul al doilea in
din prima ecuatie
in a doua si se obtine o ecuatie de gradul al doilea in 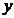
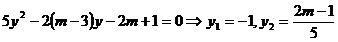
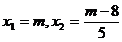
b)Sistemul admite solutii cu numere
intregi negative daca 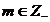
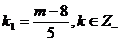
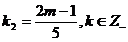 ; unde
; unde 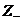 este multimea
numerelor intregi negative.
este multimea
numerelor intregi negative.
Din 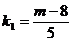 , avem
, avem 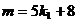 .Pentru aceste valori le lui
.Pentru aceste valori le lui 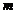 se obtine
se obtine
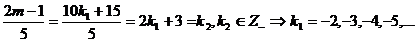
Deci sistemul
admite solutiile intregi negative
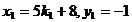
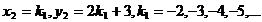
c)Pentru 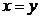 sistemul se scrie
sistemul se scrie
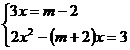
Eliminam 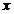 si obtinem
ecuatia de gradul al doilea in
si obtinem
ecuatia de gradul al doilea in 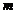
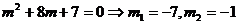
Pentru 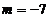 ,obtinem
,obtinem 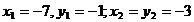 , iar pentru
, iar pentru 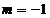 se obtine
se obtine
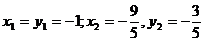
4)Sa se rezolve, in 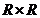 ,sistemul
,sistemul
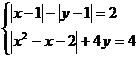
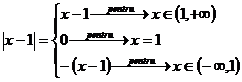
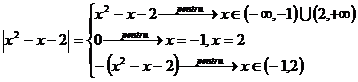
Cazul nr 1: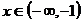
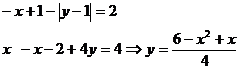
 Prima ecuatie devine
Prima ecuatie devine
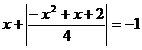 , pentru
, pentru 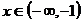 se scrie
se scrie
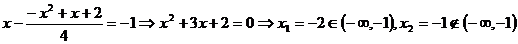
Iar pentru 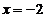 se obtine
se obtine 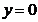
Cazul nr 2: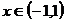
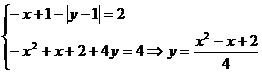
Care inlocuit in prima ecuatie da:
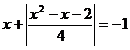
Insa,
pentru 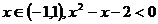 si deci
si deci 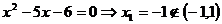
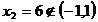 , sistemul nu admite solutii.
, sistemul nu admite solutii.
Cazul nr 3: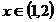
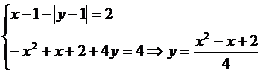
Prima ecuatie devine
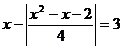 care pentru
care pentru 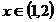 se mai scrie
se mai scrie
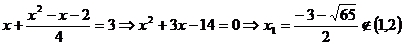

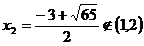 si sistemul nu
admite solutii.
si sistemul nu
admite solutii.
Cazul
nr 4: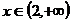
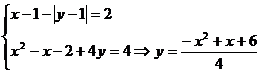
Prima ecuatie se scrie
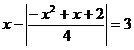 sau pentru
sau pentru 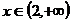
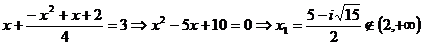
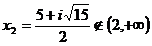 , sistemul nu admite solutii.
, sistemul nu admite solutii.
Cazul
nr 5: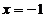
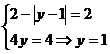
Cazul
nr 6: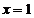
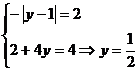 , prima ecuatie
nu are loc
, prima ecuatie
nu are loc
Cazul
nr 7: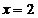
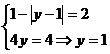 , prima ecuatie
nu este verificata
, prima ecuatie
nu este verificata
Solutiile sistemului sunt: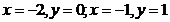
5) a)Sa se rezolve sistemul
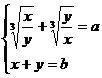
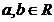
b)Sa se determine 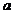 si
si 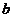 pentru care
solutiile sistemului sunt
pentru care
solutiile sistemului sunt
1)rationale 2)intregi 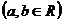
a)
Ridicam prima ecuatie la puterea a treia
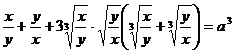
Se obtine
sistemul
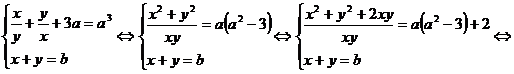
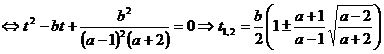
Deci
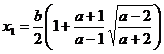
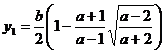
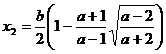
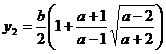
b)
Solutiile sistemului sunt rationale daca 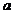 si
si 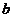 sunt rationali
si
sunt rationali
si
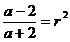 cu
cu 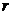 rational
rational 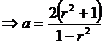
Sistemul admite
ca solutii numer intregi daca 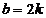 ,
, 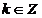 si
si
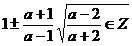 sau
sau 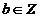 si
si 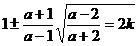 ,
, 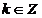
Dar
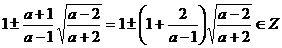
Daca 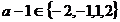 (a-1 este un divizor
al lui 2) si
(a-1 este un divizor
al lui 2) si 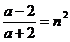 , cu
, cu 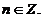
Unica valoare a
lui 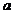 care satisface aceste
conditii este
care satisface aceste
conditii este 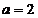 si solutia
sistemului este
si solutia
sistemului este 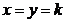 , cu
, cu 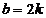 ,
, 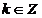


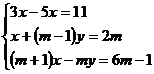
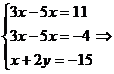 incompatibil
incompatibil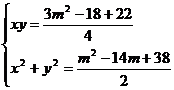
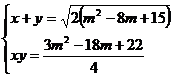
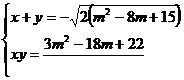
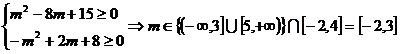
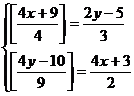
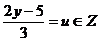 ,
, 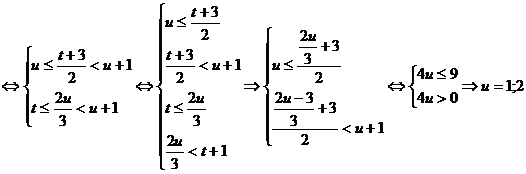
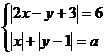
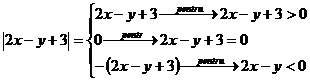
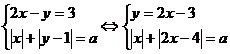
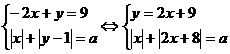
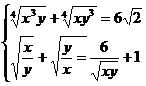
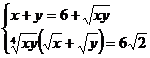
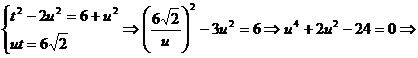
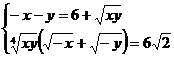
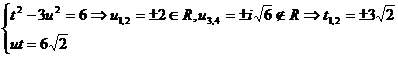
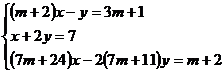
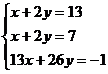 (incompatibil)
(incompatibil)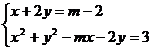
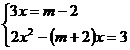
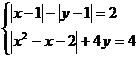
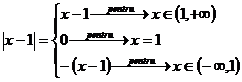
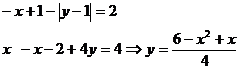
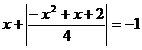 , pentru
, pentru 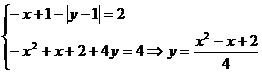
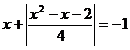
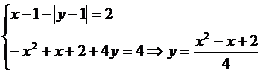
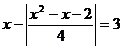 care pentru
care pentru 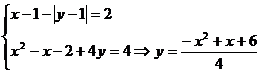
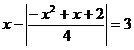 sau pentru
sau pentru 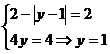
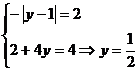 , prima ecuatie
nu are loc
, prima ecuatie
nu are loc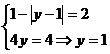 , prima ecuatie
nu este verificata
, prima ecuatie
nu este verificata