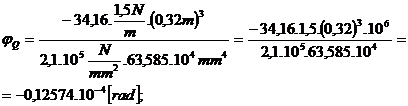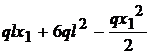Teoremele lui Castigliano
Daca avem o bara incarcata ca in
figura 10:
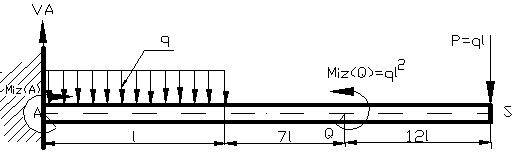
Figura 10
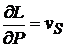 ; sageata in punctul S ,
iar
; sageata in punctul S ,
iar 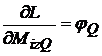 ;
;
rotirea sectiunii
transversale din punctul Q .
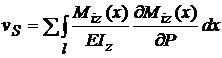 ;
; 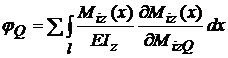 ;
;
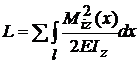 ; L fiind lucrul mecanic elastic de
deformatie
; L fiind lucrul mecanic elastic de
deformatie
inmagazinat intr-o bara supusa la
incovoiere.
In cazul in care se cere
sa calculam in (S) si
rotirea sectiunii
transvesale, trebuie sa introducem in S un moment incovoietor concentrat fictiv Miz (S) = 0 kN.m , apoi se
calculeaza VA si Miz
(A) functie de Miz( S) , la sfarsitul rezolvarii problemei se
face
Miz (S) = 0 kN.m.
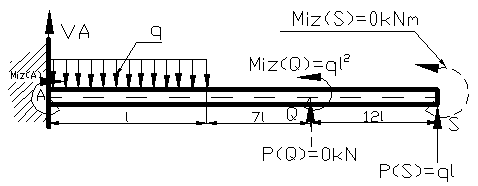
Figura
11
In mod analog daca se cere sageata
in Q , se introduce in sectiunea
transversala din punctul Q , se introduce
o forta concentrata fictiva
PQ = 0 [ kN ] si se procedeaza in acelasi mod , adica
calculam forta de reactiune VA , respectiv momentul
de reactiune Miz(A) si in functie de PQ ,
apoi la sfarsitul rezolvarii problemei se inlocuieste
PQ = 0 [ kN ] .
Problema nr. 6
Sa se
calculeze sageata si rotirea sectiunii transversale din Q,
pentru bara din figura 12 , stiind ca : E = 2,1.105 N/mm2
; q = 1,5 N/m ; l = 0,32 m , sectiunea
transversala fiind circulara cu diametrul 60 mm.
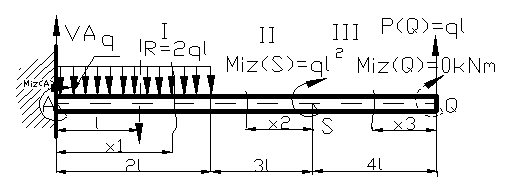
Figura
12
Deoarece in punctul Q nu avem moment
incovoietor concentrat,
se
introduce un moment incovoietor concentrat fictiv
Miz(Q) = 0 [ kN.m ] la urma se introduce valoarea
lui numerica .
Se calculeaza VA si Miz (A) functie de Miz(
Q) si de forta concentrata PQ cu mentiunea
ca la sfirsitul rezolvarii problemei se inlocuiesc
Miz( Q ) = 0 [ kN .m ] si PQ = ql .
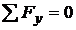 ; VA - 2ql + PQ =
0 ; VA = 2ql - PQ ;
; VA - 2ql + PQ =
0 ; VA = 2ql - PQ ;
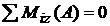 ;
; 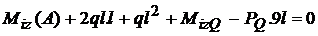 ;
;
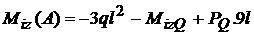 .
.
La
aplicarea teoremelor lui Castigliano pentru inceput trebuie sa se lucreze cu tabelele , fiind mai
usor de calculat, dupa o anumita perioada de acomodare cu
aceste metode atunci se poate trece peste anumite etape de calcul .
Regiunea
intai;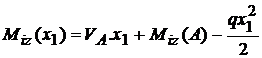 ;
;
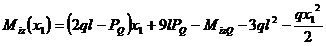 ;
;
Observatie
Pentru
regiunea a II-a este bine sa se ia
originea in punctul S pentru ca se usureaza calculul
integralelor, de exemplu daca avem :
cazul( I ) ; 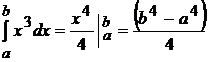 ; cazul ( II )
; cazul ( II ) 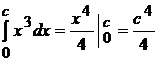 ; in cazul al doilea este mai avantajos de calculat.
; in cazul al doilea este mai avantajos de calculat.
|
Regiunea
|
Miz(x)
|
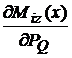
|
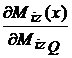
|
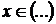
|
|
intai
|
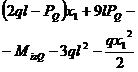
|
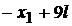
|
|
(0;2l)
|
|
a II-a
|
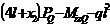
|
4l + x2
|
|
(0;3l)
|
|
a III-a
|
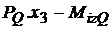
|
x3
|
|
(0;4l)
|
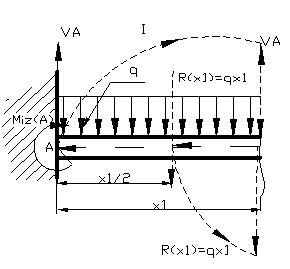
Figura
13
Regiunea
a II-a
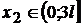 ;
; 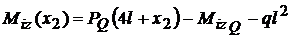 ;
;
Regiunea
a III-a
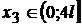 ;
; 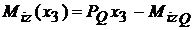 ; tabelul este
indicat
; tabelul este
indicat
sa se faca , deoarece
ajuta la calcul.
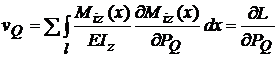 ;
; 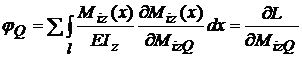
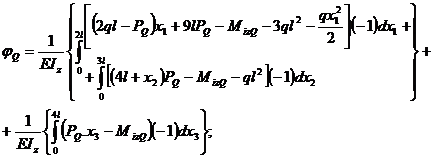
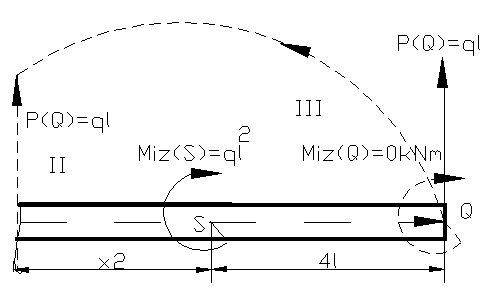
Figura
14
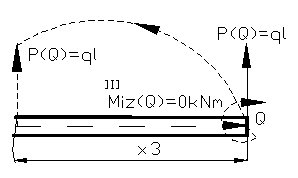
Figura
15
acum se fac inlocuirile cu valorile lor
: PQ = ql ; MizQ = 0 [ kN.m ]
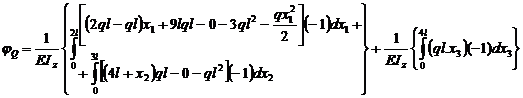
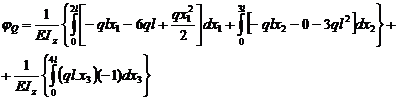
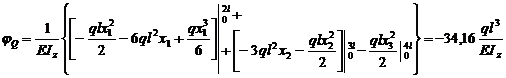
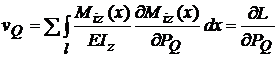 ;
;
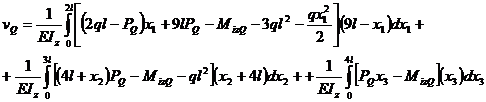
Acum se inlocuiesc PQ si MizQ cu valorile lor si anume
: PQ = ql ;
MizQ
= 0 [ kN.m ]
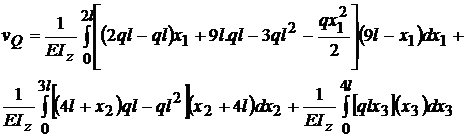
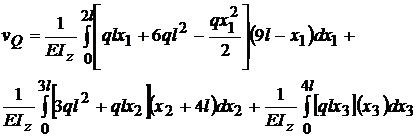 ;
;
de
unde 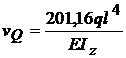 .Dupa ce s-a facut primul tabel se poate face
si un al doilea tabel cu valorile inlocuite pentru PQ si MizQ:
.Dupa ce s-a facut primul tabel se poate face
si un al doilea tabel cu valorile inlocuite pentru PQ si MizQ:
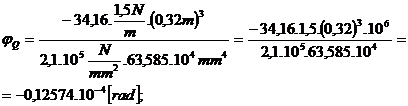
|
Regiunea barei
|
Miz(x)
|
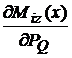
|
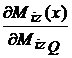
|
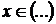
|
|
intai
|
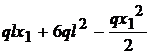
|
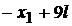
|
|
(0;2l)
|
|
a II-a
|
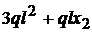
|
4l + x2
|
|
(0;3l)
|
|
a III-a
|
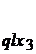
|
x3
|
|
(0;4l)
|




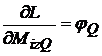 ;
; 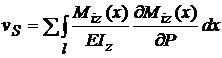 ;
;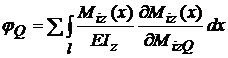 ;
;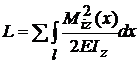 ; L fiind lucrul mecanic elastic de
deformatie
; L fiind lucrul mecanic elastic de
deformatie

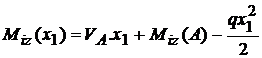 ;
; 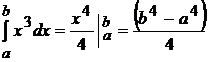 ; cazul ( II )
; cazul ( II ) 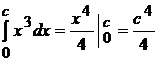 ; in cazul al doilea este mai avantajos de calculat.
; in cazul al doilea este mai avantajos de calculat.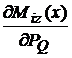
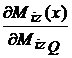
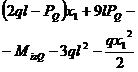

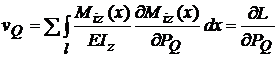 ;
; 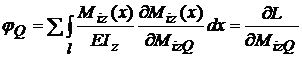
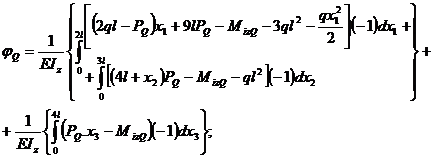


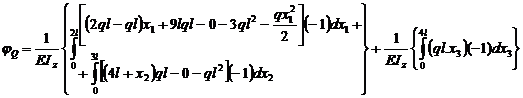
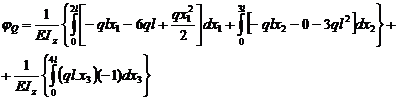
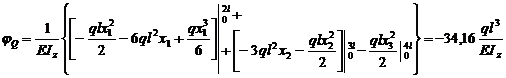
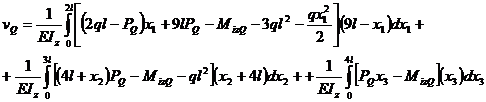
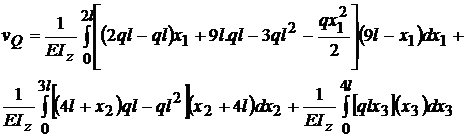
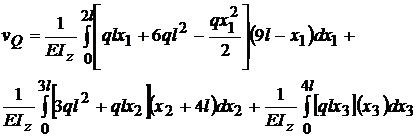 ;
;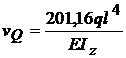 .Dupa ce s-a facut primul tabel se poate face
si un al doilea tabel cu valorile inlocuite pentru PQ si MizQ:
.Dupa ce s-a facut primul tabel se poate face
si un al doilea tabel cu valorile inlocuite pentru PQ si MizQ: