Strategii de predare-invațare-problematizare

Strategii de predare-invațare-problematizare

Strategia didactica poate fi definita ca o modalitate de organizare si conducere a procesului de predare-invatare-evaluare, pe baza combinarii eficiente a mijloacelor de invatamant si a formelor de grupare a elevilor, in functie de continutul si cunostintele anterioare, vizand obtinerea de performante maxime, in raport cu obiectivele pedagogice fixate.

Profesorii isi stabilesc strategiile didactice pornind de la conceptia contemporana si conceptia personala , avand in vedere continutul si obiectivele situatiilor de instruire, diferite tipuri de invatare, principiile si legile didactice, sistemul de gandire si, nu in ultimul rand, nivelul de cunostinte al elevilor sau spatiul scolar unde se desfasoara lectia precum si timpul alocat acesteia.

Dintre strategiile didactice mai des utilizate mentionez:

- strategii inductive

- strategii deductive

- strategii transductive(explicatii prin metafore)

- strategii analogice

- strategii mixte(inductiv- deductive, deductiv-inductive)

- strategii algoritmice

- strategii euristice de elaborare a cunostintelor prin efort propriu de gandire, folosind problematizarea, descoperirea, modelarea, formularea de ipoteze, dialogul euristic, avand ca efect stimularea creativitatii.

Ma voi referi pe scurt la problematizare.

Ca modalitate metodologica, problematizarea conduce pe elevi la rezolvarea unor ,,situatii-problema'', care apar intre nevoia gasirii solutiei unei probleme si experienta redusa sau priceperea nesatisfacatoare a elevului.Misiunea profesorului este dificila deoarece, el trebuie sa descopere, sa inventeze, sa genereze ,,situatii- problema'' care sa solicite gandirea elevilor.Pentru ca problematizarea sa fie eficienta este necesar ca profesorul sa respecte unele conditii in formularea situatiilor-problema:

sa asigure un bagaj minim de informatii cerute de probleml

-sa organizeze informatiile astfel incat intrebarea-problema sa fie insotita de directionarea spre rezolvare a gandirii elevilor

-sa se raporteze la cunostinte dobandite anterior.

Aplicații:

1)   Inelul (Z,+, ) este euclidian. Intr-adevar , in acest inel are loc teorema impartirii cu rest pentru numere intregi , si anume:

a,bIZ , b q,rIZ a.i. a=bq+r . unde 0 r ¸| b| .

Mai mult q si r sunt unice.

Considerind functia f: Z- N, f(n)=| n |, rezulta clar ca inelul Z  impreuna cu f este euclidian (satisface conditiile 1 si 2). Mentionam ca teorema impartirii cu rest la numere intregi o vom demonstra in paragraful 1 al capitolului III.

2)   Orice corp este inel euclidian. Intr-adevar, daca K este un corp, consideram functia f : K- N definita prin f(a)=1, aIK ,a 0 . Aceasta functie satisface 1 si 2.

3)   Inelul K[x] al polinoamelor cu coeficienti intr-un corp K pentru care functia f :K[x] - N, definita prin f(g)=grad(g), gIK[x] , g 0 , este un inel euclidian.

Intr-adevar, daca g,h IK[x], g 0 si g/h, atunci h=gg', cu g'IK[x], deci    grad(g) grad(h), adica f(g) f(h). Deci conditia 1 este indeplinita.

Sa verificam proprietatea 2. Fie f,gIK[x] cu g 0. Daca grad(g)=0, atunci f=g(g f), deoarece g 0 din K, deci inversabil si afirmatia este dovedita, adica este verificata proprietatea 2. Daca grad(g)>0, atunci vom face o inductie dupa gradul lui f. Daca grad(f)<grad(g), in particular, pentru grad(f)=0, din relatia f=g 0+f, rezulta 2.

Presupunem ca 2 afost verificata pent 434q1619e ru toate polinoamele f, cu grad(f)<n.Fie atunci f un polinom de grad n, 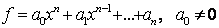si g un polinom de gradul m,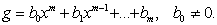

Putem presupune ca m n , conform celor demonstrate mai sus. Atunci, polinomul 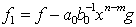are gradul cel mult n-1, deoarece termenii de gradul cel mai mare se reduc , deci grad(f1)<grad(f). Din ipoteza inductiva rezulta, atunci ca exista q,rIK[x] a.i. f1=gq+r, unde r=0 sau grad(r)<grad(g). Atunci avem: 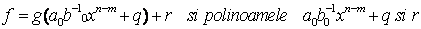satisfac proprietatea 2. Polinoamele q si r IK[x] , numite citul si restul , astfel incit  f=qg+r, r=0 sau grad(r)<grad(g); In cazul inelului K[x] sunt chiar unice (ca si la Z , de altfel). Dar unicitatea acestora nu este necesara in formula de impartire cu rest , in cazul inelului euclidian.

4)   Fie inelul Z[i] al intregilor lui Gauss. Am vazut ca elementele sale inversabile sunt -1,1,-i,i.  Fie 1+iIZ[i], acesta este neinversabil. Sa aratam ca 1+i este ireductibil. Sa presupunem ca 1+i=uv. Atunci |1+i | = |u | |v |; deci |u | |v |=2, de unde rezulta ca |u | =2 si |v |=1 sau invers. Deci, sau u este asociat cu 1+i si v inversabil, sau invers. Prin urmare,1+i este element ireductibil in Z[i]. In schimb, 2IZ[i] este reductibil. El se descompune intr-un produs de forma 2=(1+i)(1-i) , unde 1+i si 1-i sunt elemente neinversabile.

Numarul 3 este ireductibil in Z[i]. Intr-adevar daca ar fi reductibil , atunci ar exista o descompunere a sa de forma 3=uv, in care u,v sunt neinversabile.

Atunci |3 |=|u | |v |=9, de unde rezulta ca |u |=3 si |v |=3, deoarece am presupus u,v neinversabile. Fie u = a+bi. Atunci |u |= a + b =3. Deci |a |,|b | 1, insa asemenea numere intregi care sa verifice egalitatea nu exista. Prin urmare, un astfel de u nu exista si, deci 3 este ireductibil in Z[i].

5)   Fie inelul Z[i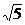], unde Z[i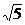]=. Fie u=a+bi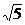, u este inversabil daca in mod necesar a + 5b =1, de unde rezulta ca u = +-1. Asadar, pentru acest inel, elementele inversabile sunt 1 si -1. Fie elementul 3IZ[i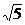]. Elementul 3 este ireductibil, caci daca 3 = uv, cu u,v neinversabile , rezulta ca |3 | =|u | |v | sau 9 = |u | |v | , adica |u | =|v | =3. Daca u = a+bi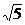, atunci 3 = a + 5b , ceea ce nu este posibil. Insa 3 nu este prim in acest inel, caci 3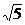/(4+i)(4-i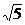)=21, iar 3 nu divide nici unul din factori. Daca 3 ar divide, de exemplu, pe 4+i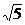, rezulta ca |3 | =9 ar divide | 4+i 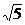|=21, ceea ce nu este adevarat. Acest exemplu arata ca reciproca punctului 1 al teoremei nu este intotdeauna adevarata, adica exista elemente care nu sunt prime. In domenii de integritate notiunile de element prim si element ireductibil sunt in general distincte.

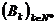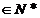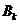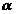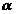
Fie și doua șiruri de matrici patratice de ordinul n cu elemente din R. Daca pentru orice k, este inversabila, sp se arate ca exista o infinitate de numere reale astfel incat + 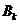este inversabila, oricare ar fi k.

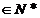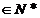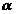
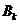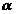
Soluție. Pentru fiecare k, scriind matricea +și dezvoltand conform definiției, constatam ca det (+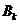) este un polinom in 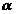, in care termenul  ce conține pe 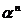are coeficientul det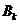

Așadar, acest polinom este nenul (are gradul n) și ca atare mulțimea radacinilor reale ale acestui polinom este finita (eventual poate mulțimea vida). Sa notam

, k =1,2,3,

Mulțimea X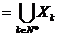este o reuniune numarabila de mulțimi finite, deci este nenumarabila.

Deoarece R nu este nenumarabilp, rezulta ca mulțimea R X este infinita.

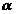
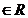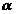
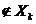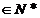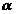
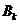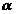
Dar pentru X, avem ,() k, deci det (+), adica+ 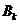este inversabila, () k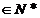. Cu acestea soluția se incheie.

Consideram o mulțime A= și legile de compoziție și pe acesta multime definita astfel

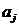=și =

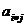
Unde 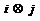este restul imparțirii lui i+j prin n, iar este restul imparțirii lui ij prin n.

Ce structura algebrica este tripletul ()?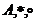

Soluție. (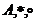) este inel izomorf cu inelul claselor de resturi modulo n, ceea ce se poate verifica cu ușurința. Aplicația (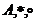)i este izomorf de inele.

Exista inele comutative unitare A astfel incat ineleul de polinoame intr-o nedeterminata A[X] sa fie izomorf cu inelul ?

Soluție. Sa presupunem ca ar exista un inel comutativ unitar A astfel incat A[X] 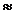Z. Cum A este subinel unitar al lui A[X], rezulta ca A este izomorf cu un subinel unitar al lui Z.

In particular, (A,+) va fi izomorf cu un sub grup nenul al grupului aidtiv (Z,+), deci exista n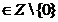astfel incat A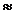Z. Dar 1 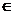A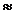Z, ceea ce este o contradicție (caci inelul Z nu este izomorf cu inelul de polinoame Z[X]. Deci nu exista inele A cu proprietatea din enunț.

9) Fie A uninel necomutativ unitar,iar a,b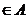. Sa se arate ca daca 1-ab este inversabil, atunci 1-ba este inversabil.

Soluție. Fie u inversul elementului 1-ab. Vom arata ca elementul v=1+bua este inversul lui 1-ba. Intr-adevar:

v(1-ba)=(1+bua)(1-ba)=1-ba+bua-buaba (1)

Dar u(1-ab=1, deci uab=u-1. Continuand in (1) rezulta:

v(1-ba)=1-ba+bua-b(u-1)a=1-ba+bua-bua+ba=1.

Analog se arata ca (1-ba)v=1. Deci 1-ba este inversabil, inversul acestui element fiind v.

Fie A un inel cu element unitate 1 și M 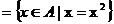mulțimea elementelor sale idempotente. Sa se demonstreze ca daca M este mulțime finita, atunci M are un numar par de elemente.

Soluție Sa observam ca daca x este element idempotent, atunci și 1-x este idempotent. Intr-adevar,

(1-x) 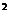=1-2x+x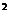=a-2x+x=1-x

Rezulta ca elementele lui M se pot grupa in perechi de forma (x,1-x).

Elementele din oricare asemenea pereche sunt distincte. Intr-adevar daca ar exista x 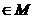cu proprietatea ca x=1- x, inmulțind cu x și ținand seama ca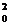 x= x, obținem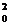 x= x- x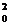, adica x= x- x deci x=0.

In felul acesta egalitatea x=1-x conduce la 0=1, contradicție.

Notand cu n numarul perechilor din M, de tipul descris mai sus, rezulta ca M are 2n elemente.