FENOMENE DE TRANSPORT
Organismele vii sunt
sisteme deschise, care in mod permanent realizeaza schimburi de
substanta, de energie si de informatie cu mediul
inconjurator. Schimburile au loc in ambele sensuri si constituie
conditia "sine qua non" de mentinere a structurii si
functionarii optime a biosistemelor.
Fenomenul de transport
spre interior (influx) si spre exterior (eflux) se manifesta la toate
nivelele de organizare ale materiei vii.
In acest capitol este
tratat transportul de impuls de catre moleculele unui lichid real, de la
un strat la altul, datorita vascozitatii lichidului, precum
si transportul de substanta, in sensul cresterii entropiei,
prin difuzie si osmoza, atunci cand exista gradienti de
concentratie, de potential sau de presiune.
1.
Vascozitate
1.1.
Coeficienti de vascozitate
Curgerea unui fluid real are loc in straturi foarte
subtiri, moleculele din acelasi strat avand aceeasi viteza,
in timp ce cele din straturile adiacente, viteze diferite. Intre moleculele
straturilor vecine, dar si intre moleculele aceluiasi strat, se
exercita forte de interactiune de tip van der Waals, care se
opun deplasarii relative a moleculelor, determinand aparitia unei
frecari interne, numita vascozitate.
Fortele de frecare interna, numite forte de
vascozitate (Fv), rezulta ca urmare a transportului de impuls
de catre moleculele lichidului de la un strat la altul.
Fortele de vascozitate sunt orientate tangential
la suprafata straturilor si in sens opus vitezei stratului respectiv
(Fig.1).
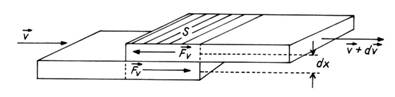
Fig. 1. Forta de vascozitate.
Forta de vascozitate pentru o curgere laminara,
cand straturile de lichid raman paralele (vezi paragraful 1.3.), este
data de legea lui Newton:
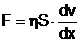 (1)
(1)
unde: h - coeficientul de vascozitate
dinamica, S - aria comuna a celor doua straturi si dv/dx -
gradientul de viteza, perpendicular pe directia de curgere.
Semnificatia
fizica a coeficientului de vascozitate dinamica: forta de frecare
dintre doua straturi cu sectiunea egala cu unitatea pentru un
gradient de viteza egal cu unitatea.
Unitatea de
masura in SI pentru h se poate deduce din legea lui Newton si este: [h]SI = N S m-2 =Poiseuille, iar ca unitate tolerata in
CGS se utilizeaza [h]CGS =dyn s cm-2 = 1P (poise).
Inversul
coeficientului de vascozitate dinamica se numeste fluiditate dinamica (j h). Deoarece densitatea (r) a lichidului joaca un rol important in curgerea
lichidului, se introduce o noua marime numita coeficient de vascozitate cinematica (n), definit:
n h r (2)
a carui unitati de masura sunt [n]SI = m2 s-1 =1dakts
(decakilostokes), respecriv [n]CGS = cm2 s-1 = 1 St (Stokes).
In general,
vascozitatea unui sistem de dispersie depinde de concentratie, din acest
motiv se utilizeaza si notiunea de coeficient de vascozitate relativa (hr
hr h h (3)
ca fiind raportul dintre coeficientul de vascozitate dinamica al
solutiei (h) si cel al solventului pur (h
Lichidele pentru care
este valabila legea lui Newton se numesc lichide newtoniene. Pentru aceste lichide, coeficientul de
vascozitate dinamica depinde de natura lichidului si de
temperatura, scazand rapid cu cresterea temperaturii. In cazul
cand temperatura ramane constanta, h pentru un lichid dat este considerat constant si nu
depinde de gradientul de viteza. Din clasa lichidelor newtoniene fac parte
un numar mare de lichide, in special lichide pure, unele solutii
coloidale de concentratii mici si majoritatea lichidelor biologice
(lichidul cefalorahidian, plasma sangvina, urina).
Lichidele care nu se
supun legii lui Newton se numesc lichide
nenewtoniene, pentru care coeficientul de vascozitate dinamica depinde
de gradientul de viteza si nu mai este constant la o temperatura
data. Din aceasta categorie fac parte solutii macromoleculare,
coloidale, suspensii (sangele).
Coeficientul de
vascozitate dinamica pentru lichidele nenewtoniene, in speta
sisteme coloidale macromoleculare, depinde de forma si concentratia
particulelor disipate, conform legii lui Einstein:
h hd (1 + kV) (4)
unde hd - coeficient de vascozitate dinamica a mediul de dispersie; V -
volumul fazei dispersate din unitatea de volum a solutiei; k -
constanta care depinde de marimea si natura particulelor
dispersate.
In Tabelul 1. sunt
prezentate valorile coeficientul de vascozitate dinamica pentru unele
lichide biologice, la cateva temperaturi.
Tabel 1. Valorile
coeficientului de vascozitate dinamica
|
Lichid
|
t
(0C)
|
h
10-3 (N
s m-2)
|
|
Apa
|
|
|
|
Lichid
cefalorahidian
|
|
|
|
Ser
sangvin
|
|
|
|
Sange
|
|
|
|
Urina
|
|
|
1.2.
Vascozitatea sangelui
La temperatura de 370C, vascozitatea sangelui este de cca. 4 ori
mai mare decat a apei, sangele fiind un lichid nenewtonian.
Sangele este un lichid complex,
fiind un sistem dispers heterogen, mai precis o suspensie de elemente figurate
(celulele) in plasma (solutie apoasa de electroliti,
neelectroliti si macromoleculare).
Procentul din volumul total al
sangelui ocupat de elementele figurate, in majoritate covarsitoare
hematii, poarta numele de hematocrit,
valoarea normala fiind cuprinsa intre 45 si 50%.
In consecinta,
vascozitatea sangelui variaza in functie de marimea
hematocritului, de viteza de curgere si de raza tubului.
Dependenta descrisa de
ecuatia lui Einstein (relatia 4.) pentru lichidele nenewtoniene este
de tip liniar. Insa, in cazul sangelui, aceasta dependenta
este aproape exponentiala (Fig. 2.). Aceasta variatie
brusca a vascozitatii relativa se explica prin faptul
ca la valori de peste 58-60% a hematocritului, apar aglomerari ale
hematiilor, acestea deformandu-se datorita presiunii dintre ele. Astfel,
imposibilitatea miscarii libere a hematiilor determina o
crestere accentuata a vascozitatii.
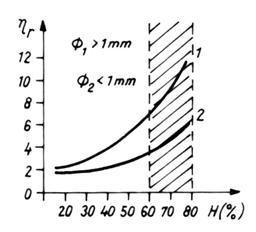
Fig. 2.
Variatia vascozitatii relative cu hematocritul
Masuratorile pentru cele doua
curbe din figura au fost efectuate cu capilare diferite: curba (1) cu F > 1mm si
curba (2) cu F < 1mm.
Dependenta coeficientului de vascozitate relativa de diametrul
capilarului este cunoscuta sub denumirea de fenomenul Fahraeus-Lindquist (Fig.3).
Matematic,
aceasta dependenta este descrisa de relatia:
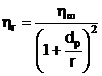 (5)
(5)
unde 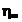 - coeficientul de vascozitate pentru un tub cu raza foarte
mare;
- coeficientul de vascozitate pentru un tub cu raza foarte
mare;
dp - diametrul particulelor
(hematii)
r - raza capilarului
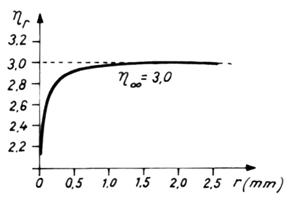
Fig.3. Variatia vascozitatii
relative a sangelui cu raza capilarului.
Variatia
coeficientului de vascozitate relativa cu raza tubului si cu viteza
de curgere se datoreaza acumularii si aranjarii hamatiilor
in zona axiala a tubului si formarii unui manson plasmatic
de vascozitate mica la contactul cu peretii vasului. Procesul are
loc la viteze de curgere mici, astfel
incat vascozitatea nu mai este influentata sensibil de variatia
vitezei in circuitul sangvin. In schimb,
cand raza tubului scade sub 0,5 mm se constata o micsorare
accentuata a vascozitatii relative, ceea ce favorizeaza
curgerea in vasele sangvine mici.
Modificari ale vascozitatii apar in diferite stari
patologice, astfel creste la hipertensiune, poliglobulie, axfixie si
scade la anemie.
Vascozitatea creste in urma consumului de alcool, cafea si
datorita existentei produsilor de dezasimilatie
acumulati in organism in perioada de oboseala. Cresterea
concentratiei de CO2 in sange duce la marirea (umflarea)
elementelor figurate, ceea ce determina cresterea
vascozitatii. Asadar, sangele venos este mai vascos decat cel
arterial.
Cresterea
vascozitatii cu scaderea temperaturii si conjugata cu
vasoconstrictia capilara determina stagnarea circulatiei
periferice, ducand la aparitia degeraturilor.
De asemenea, cresterea
vascozitatii determina o crestere a efortului inimii pentru
mentinerea unui debit normal, deci o crestere a tensiunii arteriale.
Vascozitatea este mai mica la
femei decat la barbati si la copii decat la adulti.
1.3. Reologia
Reologia studiaza curgerea
lichidelor reale (h>0), unde au loc
pierderi datorita frecarilor dintre straturile de lichid.
In
cazul lichidelor newtoniene curgerea nu influenteaza coeficientul de
vascozitate dinamica, deoarece la o temperatura data acesta are
o valoare constanta. In schimb, coeficientul de vascozitate al lichidelor
nenewtoniene este dependent de conditiile de curgere.
Exista
doua regimuri de curgere pentru un lichid vascos: laminar si
turbulent.
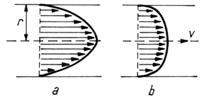
Fig. 4. Profilul vitezelor; a) curgere
laminara si b) curgere turbulenta.
In curgerea laminara straturile de
lichid se deplaseaza paralel unele fata de altele, incat liniile
de curent nu se intersecteaza. Viteza de curgere nu are componenta
radiala. Curgerea laminara poate fi stationara sau
nestationara. In regim laminar, profilul vitezelor in sectiune
transversala este parabolic, avand valoare maxima de-a lungul axului
tubului (Fig.4.a).
Curgerea turbulenta se caracterizeaza prin traiectorii
dezordonate ale particulelor de lichid, astfel incat straturile se
amesteca intre ele. Acest regim de curgere apare daca viteza
lichidului creste depasind o valoare critica (vc),
si/sau sectiunea tubului se mareste. In acest caz,
exista componente radiale ale vitezei de curgere. Curgerea turbulenta
este numai nestationara.
Daca in timpul curgerii apar miscari de rotatie (vartejuri,
turbioane) curgerea turbulenta devine curgere
turbionara. In regim turbulent, profilul vitezei nu mai este parabolic
(Fig.4.b). Curgerea turbulenta este consumatoare de energie.
Caracterul
laminar sau turbulent al curgerii unui fluid printr-un tub cu peretii
rigizi se poate stabili cu ajutorul numarului
lui Reynolds (Re):
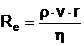 (5)
(5)
unde v - viteza de curgere, r -
raza tubului, r -
densitatea fluidului si h - coeficientul vascozitate
dinamica a fluidului.
S-a
vazut ca pentru conditii date (lichid si tub) exista o
viteza de curgere critica (vc), peste care curgerea devine
turbulenta, viteza care este corespunzatoare unui numar
Reynolds critic, a carui valoare este 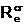 = 1000. In
functie de aceasta valoare exista regimurile de curgere:
= 1000. In
functie de aceasta valoare exista regimurile de curgere:
a)
Re < 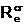 -curgere
laminara;
-curgere
laminara;
b)
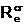 = 1000 < Re < -curgere nestabila;
= 1000 < Re < -curgere nestabila;
c)
Re > 2000
curgere turbulenta.
1.4. Notiuni de hemodinamica
Hemodinamica
este un capitol al biofizicii, care se ocupa de fenomenele fizice legate
de circulatia sangelui.
Sistemul
cardiovascular este alcatuit din inima, cu rol de pompa
aspiro-respingatoare, si o retea continua de vase inchise
cu sectiuni diferite (artere,vene si capilare) prin care circula
sangele.
Circulatia
sangvina, in afara parametrilor ce caracterizeaza curgerea
oricarui lichid (vascozitate, gradient de presiune, diametrului
conductei), are si particularitati datorita
proprietatilor specifice ale sangelui si ale peretilor
vaselor sangvine:
sangele este un lichid nenewtonian;
peretii vaselor sangvine sunt
elastici;
circulatia sangelui nu este
continua, ci pulsatorie.
Vascozitatea
relativ mare a sangelui, neomgenitatea lui, expulzarea ciclica sub
presiune mare, precum si forma diferita si variabila a
vaselor sangvine determina o curgere care nu este strict laminara,
profilul vitezei nefiind parabolic. Curgerea turbulenta propriu-zisa
se observa, in mod normal, doar in partea initiala a aortei
si a arterei pulmonare. In celelalte vase mari apare o
microturbulenta, adica un regim intermediar intre curgerea
laminara si cea turbulenta. Acest tip de curgere favorizeaza
schimburile intre sange si peretii vasului, precum si
omogenizarea substantelor dizolvate.
Pentru ca
hematiile sa poata sa treaca prin capilare, acestea se
orienteaza perpendicular pe axul tubului. In cazul cand diametrul
capilarului este mai mic decat cel al hematiilor, acestea se deformeaza
elastic, pentru a fi posibila curgerea sangelui.
Viteza de
curgere a sangelui in diferite zone ale aparatului circulator depinde de
sectiunea si rezistenta la curgere a vaselor sangvine. Aria
totala a sectiunii transversale a capilarelor este de 700-800 ori mai
mare decat a aortei, deci viteza medie in capilare va fi de 103
mai mica decat in aorta unde valoarea mediei este de 0,5 m/s, iar la
nivelul capilarelor de 0,5 mm/s. (vezi Fig.6)
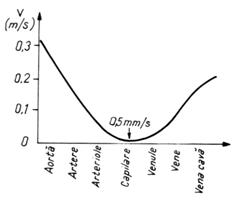
Fig. Variatia
vitezei medii a sangelui in vasele sangvine.
Presiunea sangelui
sufera variatii mari in aparatul circulator. Este maxima la
nivelul orificiilor ventriculare ale marilor artere (aorta): 120-130 mm
Hg, scade la nivelul capilarelor: 10-30 mm Hg, si ajunge la valoarea
minima de 2-5 mm Hg la nivelul marilor vene.
Presiunea
arteriala este caracterizata de doua valori: maxima, care
corespunde presiunii ventriculare in timpul sistolei (ps), si
minima, care este presiunea diastolica (pd). Tabelul 2.
sunt prezentate presiuni arteriale pentru organismele vii.
Tabelul 2. Valori ale presiunii arteriale
Organism
|
ps
(mm Hg)
|
pd
(mm Hg)
|
|
om
cal
caine
|
|
|
Curgerea turbulenta este
consumatoare de energie si s-a constat ca la mamifere exista o
adaptare a arborelui cardiovascular, pentru evitarea acestui tip de curgere.
Tinand
cont de valoarea critica a numarului Reynolds, pentru o curgere
laminara trebuie indeplinita conditia:
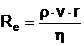 < (6)
si de relatia pentru debitul
sangvin:
< (6)
si de relatia pentru debitul
sangvin:
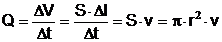 (7)
(7)
Combinand relatiile (6)
si (7) rezulta ca valoarea minima a razei vasului sangvin
trebuie sa satisfaca urmatoarea inegalitate:
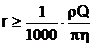 (8)
(8)
Stiind ca r = 1,1 g/cm3 si h = 0,03 Poise,
avem:
r 0,013Q (9) In
figura 7. sunt prezentate valorile experimentale ale ale razelor aortei umane
si ale unor specii de mamifere.
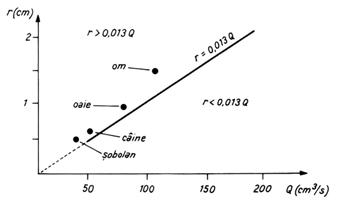
Fig. 7. Valori ale razei aortei pentru diferite
mamifere.
Se
stie ca turbulenta poate sa apara la nivelul aortei
unde viteza sangelui este cea mai mare. In aorta umana debitul sangvin
este Q = 100 cm3/s, introducand aceasta valoare in relatia
(9) se obtine r 1,3 cm.
Experimental, pentru raza aortei s-agasit valoarea rexp =1,5 cm.
Se
poate constata ca relatia (9) este satisfacuta si
pentru alte mamifere, ceea ce arata ca natura vie poate sa evite
aparitia curgerii turbulente, care este consumatoare de energie
metabolica.
2. Difuzia
Difuzia reprezinta
un transport de substanta (atomi, molecule, ioni sau complexe
moleculare) intre zone de concentratie sau potential diferite,
datorita agitatiei termice.
Fenomenul
de difuzie are loc in mod spontan, fara consum de energie, deci
pasiv, in sensul cresterii entropiei, adica tinzand spre echilibru termodinamic.
Difuzia
pasiva este cea mai intensa la gaze, unde viteza termica a
moleculelor este foarte mare, si cea mai lenta la solide, unde
moleculele (ionii) au pozitii relativ fixe in spatiu.
Intre
doua zone de concentratie diferita exista un gradient de
concentratie dC/dx, care determina aparitia unui flux Jc
ce se manifesta prin transport de substanta de la zona de
concentratie mare spre cea de concentratie mica. Difuzia
inceteaza cand gradientul de concentratie devine nul,
potentialul chimic este acelasi in tot sistemul, iar entropia atinge
valoarea maxima.
2.1. Legile lui Fick (legile difuziei)
Din punct de
vedere cantitativ, fenomenul de difuzie este descris de cele doua legi ale
lui Fick. Prima se refera la viteza de transport, iar cea de a doua la
viteza de variatie a concentratiei.
Prima lege a lui Fick: cantitatea de substanta ce
difuzeaza normal printr-o
suprafata S in unitatea de timp este proportionala cu
gradientul de densitate, adica:
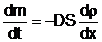 (6)
(6)
unde D - coeficient de difuzie,
se masoara in SI in m2/s; r - densitatea
moleculelor difuzate.
sau
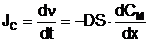 (7)
(7)
CM - concentratia
molata
iar enuntul legii: fluxul molar printr-o suprafata S este proportional cu
gradientul de concentratie
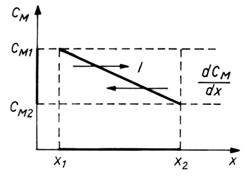
Fig.8. Variatia concentratiei intr-un
sistem dispers (CM1 > CM2 )
Semnul "-"
arata ca fluxul are loc in sens invers gradientului de
concentratie (Fig.8.).
Coeficientul de
difuzie (D) variaza direct proportional cu temperatura (T), invers proportional
cu volumul particulelor ce difuzeaza, depinzand si de forma lor.
Domeniul de valori pe care le poate lua coeficientul de difuzie este foarte
mare, astfel: pentru gaze D 10-5 m2/s,
solutii reale D 10-9
m2/s, solutii coloidale liofobe D 10-10
m2/s, solutii macromoleculare D 10-11
m2/s.
In cazul
particulelor coloidale de forma sferica, coeficientul de difuzie este
dat de relatia lui Einstein:
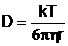 (8)
(8)
unde: k - constanta lui Boltzmann, h - coeficientul
de vascozitate dinamica, r - raza particulei.
Se
constata ca D este invers proportional cu rezistenta la
inaitare R, data de ecuatia lui Stokes:
R
= 6phrv (9)
unde: v - viteza particulei.
In
Tabelul 3. sunt prezentate valori ale coeficientului de difuzie pentru diferite
molecule proteice de interes biologic.
Tabelul 3.
Coeficienti de difuzie pentru unele molecule proteice
|
Proteina
|
D
10-11(m2/s)
|
Proteina
|
D
10-11(m2/s)
|
|
Mioglobina (bou)
Hemoglobina (cal)
Hemoglobina (om)
Serrumalbumina (cal)
Serrumalbumina (om)
|
|
Serrumglobina (om)
Lisosima (om)
Ureaza (om)
Pepsina (porc)
Insulina (bou)
|
|
Legea a doua a lui Fick: viteza
de variatie a concentratiei in orice punct al sistemului de dispersie
este proportionala cu variatia spatiala a gradientului
de concentratie, adica:
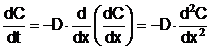 (10)
(10)
Aceasta lege nu va fi
tratata in acest capitol.
2.2. Difuzia prin membrane
Membrana
reprezinta o pelicula de grosime foarte mica, care desparte
medii de dispersie cu caracteristici fizico-chimice diferite. Ea
actioneaza ca o bariera fizica intre doua fluide, dar
permite un anumit grad de comunicare intre acestea.
O
membrana este caracterizata prin grosimea, d, si premeabilitatea,
P, care se defineste ca:
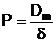 (11)
(11)
unde Dm este
coeficientul de difuzie al membranei. Permeabilitatea in SI se masoara m/s.
Sensul
fizic al permeabilitatii este: viteza de patrundere a diferitelor substante prin
membrana in conditii de concentratii date, fiind
determinata de structura membranei, iar pentru aceeasi membrana
de tipul particulei difuzante. Deci, permeabilitatea trebuie determinata pentru fiecare
sistem difuzant in parte.
Din
punct de vedere al permeabilitatii, membranele pot fi clasificate in
urmatoarele categorii:
membrana
impermeabila - nu permite traversarea ei nici de solvent si
nici de solvit;
membrana
permebila - este permeabila atat pentru solvent cat
si pentru solvit;
membrana
selectiv permeabila - este permeabila numai pentru
anumiti solventi si solviti. La randul ei se clasifica
in:
membrana
semipermeabila - permeabila numai pentru solventi;
membrana
ireciproc permeabila - are permeabilitate diferita
pentru cele doua sensuri ale aceluiasi solvit.
In organismele vii se gasesc membrane
permeabile si selectiv permeabile. Membranele biologice sunt caracterizate
prin permeabilitati foarte mari pentru apa, deorece componentele
membranei se afla in stare hidratata. De asemenea au
permeabilitati ridicate pentru anumite molecule polare (glucoza,
uree) si pentru unii ioni (K+, Na+. Cl-
etc). Pentru alte substante sunt impermeabile, ceea ce determina
acumularea unor anumite molecule pe cele doua fete ale membranei
si, implicit, aparitia unor fenomene si procese la nivelul lor
3. Osmoza
Osmoza repezinta transportul de solvent
printr-o membrna semipermeabila, care desparte doua
compartimente continand aceasi solutie, dar de concentratii
diferite. Sensul fluxului osmotic este de la concentratie mica a
solvitului spre concentratie mare a solvitului.
Acest proces
decurge spontan, deci pasiv, si daca nu este oprit duce la egalizarea
concentratiei solvitului in cele doua compartimente.
3.1. Presiunea osmotica
Fenomenul de osmoza poate fi pus in evidenta
realizand un experiment in care se utilizeaza un vas mare (1) ce
contine un solvent pur (apa) si un dispozitiv numit osmometru
(2), format dintr-un tub, care in partea inferioara este prevazut cu
o membrana semipermeabila (vezica de porc). In tub se gaseste
o solutie cu acelasi solvent (solutie de zaharoza).
Transportul
solvitului fiind imposibil, apre un flux de solvent dinspre vasul mare spre
osmometru, ceea ce determina crestera volumului de solutie
si implicit nivelul lichidului din tub (Fig.9). Deoarece membrana este
impermeabila pentru solvit, acesta nu poate patrunde in vasul mare,
ceea ce cauzeaza neegalizarea concentratiilor. Insa, se
obtine o diluare a solutiei din tub prin patrunderea solventului
pur.
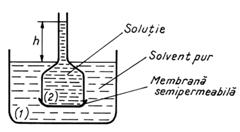
Fig.9. Fenomenul de osmoza.
Echilibrul se
stabileste numai atunci cand presiunea hidrostatica exercitata
de lichidul ce a urcat in tub egaleaza presiunea exercitata de
solutie, numita presiune
osmotica (p
p r g h (12)
unde r - densitatea
solutiei si g - acceleratia gravitationala.
In
cazul in care o membrana semipermeabila separa doua
solutii de concentratii diferite si, din exterior, asupra
solutiei mai concentrate se exercita o presiune foarte mare, se
constata ca solventul difuzeaza, in mod fortat, de la
solutia mai concentrata spre cea mai diluata, fenomen cunoscut
sub numele de osmoza inversa.
Acest
fenomen are importante aplicatii, de exemplu, este utilizat in
instalatiile pentru desalinizarea apei.
Se
intalneste la animalele acvatice si la unele pasari, care
isi asigura apa potabila din apa de mare, care fiind foarte
sarata are si o presiune osmotica mare.
Van't
Hoff a facut o analogie intre presiunea exercitata de o solutie
diluata de neelectrolit si presiunea exercitata de un gaz,
enuntand legea:
Presunea osmotica, p, exercitata de o solutie
diluata de neelectrolit este numeric egala cu presiunea pe care ar
exercita-o solvitul, daca la
temperatura data s-ar afla in stare gazoasa si ar ocupa singur
un volum egal cu al solutiei:
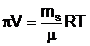 (13)
(13)
relatie care exprima legea lui van't Hoff
unde: V - volumul solutiei; ms-
masa solvitului; m - masa
molara a solvitului; R - constanta universala a gazelor; T -
temperatura absoluta a solutiei.
Daca se tine cont
ca ms/m n reprezinta
numarul de moli de solvit, iar n/V = CM
concentratia molara a solutiei, relatia (13) devine:
p = CMRT (14)
relatie ce reprezinta o
alta forma a legii lui van't Hoff.
Se
constata ca pentru solutii diluate de neelectrolit presiunea
osmotica depinde numai de concentratia solutiei si de
temperatura.
Legea lui van't
Hoff nu este valabila pentru solutii concentrate aflate la
temperaturi mai mari de 40 0C, pentru solutii de
electrolit si macromoleculare.
3.2. Osmoza in biosisteme
Osmoza este
implicata in multe fenomene fiziologice ce au loc la diferite nivele de
organizare a materiei vii. Intervine in procesele de transport al apei si
al substantelor nutritive in organism, in mentinerea volumului
si arhitecturii celulare, a metabolismului celular.
La plante, de exemplu, apa incarcata cu
substantele nutritive dizolvate din sol patrunde prin osmoza in
radacinile plantelor, iar in asociere cu fenomenul de capilaritate
asigura ascensiunea sevei in plante.
In tesuturi
osmoza are efecte mecanice, determinand o stare de tensiune mecanica,
numita turgor. Astfel, la
plantele cu membrana celulozica, prin patrunderea apei prin
osmoza in celule, tesuturile vegetale devin mai consistente si
au o rezistenta mecanica ridicata.




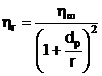 (5)
(5) 




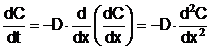 (10)
(10) 