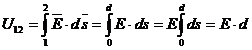Calculul capacitatii unui condensator

Calculul capacitatii unui condensator

Pentru calculul capacitatii unui condensator electric se fac urmatoarele ipoteze:

a. Se presupune condensatorul incarcat cu sarcinile .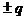

b. Se determina intensitatea campului electric dintre armaturi.

c. Se calculeaza potentialele armaturilor, respectiv diferenta de potential dintre acestea (tensiunea electrica intre cele doua borne ale condensatorului).

d. Se calculeaza capacitatea condensatorului.

Exemplu

Calculul capacitatii unui condensator plan.

Se considera condensatorul plan din fig. 3.4.3. Dielectricul se considera omogen si izotrop, avand permitivitatea 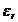; d - distanta dintre armaturi - este mult mai mica in raport cu lungimea armaturii.

Se duce o suprafata inchisa 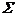prin armatura pozitiva a condensatorului si prin dielectric, aceasta suprafata avand aria laterala 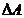perpendiculara pe liniile de camp. Aria unei armaturi a condensatorului este A. Se parcurg, pentru calculul capacitatii, etapele aratate mai sus.

a.  Se presupune condensatorul incarcat cu sarcinile +q si -q.

b. Pentru determinarea intensitatii campului electric se aplica legea fluxului electric suprafetei elementare inchise :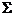

deoarece 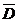si 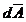sunt omoparalele pe fata laterala inferioara a lui 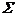, iar suprafat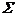a contine in interior sarcina ; .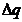

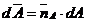Ca urmare, se poate scrie:

sau, extinzand la intreaga suprafata a armaturii:

sarcina fiind uniform repartizata pe suprafata armaturii.

Dielectricul fiind considerat liniar, i se poate aplica relatia vectoriala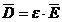, respectiv scalara 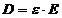, cei doi vectori fiind omoparaleli.

In aceste conditii se poate calcula E:

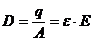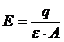c. Calculul tensiunii intre armaturi se poate face acest in acest caz utilizand relatia (3.4.9), obtinuta din forma locala a teoremei potentialului electrostatic:

Pentru aceasta s-a considerat ca originea sistemului de coordonate este pe armatura 1, campul dezvoltandu-se dupa directia O_x. Inlocuind pe E cu rel (3.4.8) rezulta:

d. Capacitatea condensatorului plan devine in acest caz: