Circuitul simplu de curent
continuu. Asocierea sensurilor de referinta pentru tensiuni, curenti si t.e.m.
Se considera
circuitul simplu de c.c. din fig. 4.3.2, compus din doua laturi cuplate
galvanic:
- o latura
generatoare (stanga) continand sursa de t.e.m. , , si rezistenta sa interna r;
, si rezistenta sa interna r;
- o latura
receptoare (dreapta) continand rezistenta de sarcina R.
|
|
|
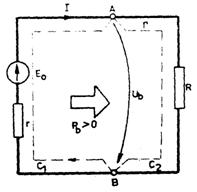
Fig. 4.3.2 Circuitul simplu de
curent continuu
|
Se aplica acestui
circuit legea conductiei electrice, curba de integrare 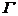 fiind dusa de-a
lungul celor doua laturi, astfel incat
fiind dusa de-a
lungul celor doua laturi, astfel incat 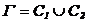 , unde
, unde 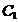 si respectiv
si respectiv  sunt curbele de-a
lungul laturilor generatoare (de la B
la A, prin stanga) si receptoare
(de la A la B, prin dreapta):
sunt curbele de-a
lungul laturilor generatoare (de la B
la A, prin stanga) si receptoare
(de la A la B, prin dreapta):
Dezvoltand
integrala se obtine:
unde:
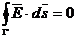 , conform teoremei potentialului electric
stationar;
, conform teoremei potentialului electric
stationar;
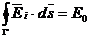 ;
;
 .
.
In aceste conditii, ecuatia circuitului
simplu de c.c. devine:
relatie
care reprezinta legea lui Ohm
pentru un circuit simplu de c.c.
Se rescrie acum
legea conductiei electrice, descompunand curba 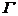 in cele doua
curbe care o compun,
in cele doua
curbe care o compun, 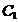 si
si  :
:
Separand
egalitatea in doua parti, pentru curba 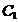 , respectiv pentru curba
, respectiv pentru curba  , se obtine:
, se obtine:
sau
Integrand termen
cu termen, relatia (4.2.7) devine:
respectiv
Aceasta
relatie reprezinta ecuatia
laturii generatoare, care contine o sursa de t.e.m. , , avand rezistenta interna r, si care are la borne tensiunea
, avand rezistenta interna r, si care are la borne tensiunea 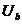 .
.
Sub alta forma, si anume 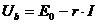 , ecuatia laturii generatoare evidentiaza
faptul ca tensiunea la bornele acestei laturi (a unei surse de c.c, in
general) este egala cu t.e.m. a sursei de tensiune, mai putin
caderea de tensiune interna pe sursa.
, ecuatia laturii generatoare evidentiaza
faptul ca tensiunea la bornele acestei laturi (a unei surse de c.c, in
general) este egala cu t.e.m. a sursei de tensiune, mai putin
caderea de tensiune interna pe sursa.
Se va scrie acum egalitatea corespunzatoare
termenilor laturii din dreapta (curba C2):
sau:
Inlocuind
integralele cu valorile lor, se obtine:
respectiv:
deoarece  , aceasta insemnand ca latura receptoare nu contine
sursa.
, aceasta insemnand ca latura receptoare nu contine
sursa.
Relatia (4.3.13)
reprezinta ecuatia laturii
receptoare, respectiv legea lui Ohm
pentru o latura pasiva de circuit.
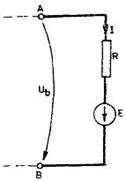
Daca latura receptoare ar contine si o
sursa (fig. 4.3.3.), ecuatia acesteia ar fi:
unde E reprezinta t.e.m. a sursei, in
acest caz sursa avand acelasi sens cu curentul.
|
|
|
Fig. 4.3.3 Ecuatia
laturii receptoare active
|
Spre deosebire de
ecuatia laturii generatoare, in cazul laturii receptoare tensiunea Ub intra cu semnul (+). In acest caz, se vede ca atat
reteaua (prin U), cat si
sursa de t.e.m. (prin E) contribuie la caderea de tensiune pe
rezistenta R.



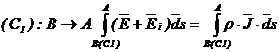

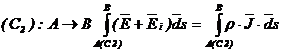
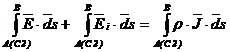
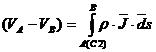
 , aceasta insemnand ca latura receptoare nu contine
sursa.
, aceasta insemnand ca latura receptoare nu contine
sursa.