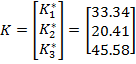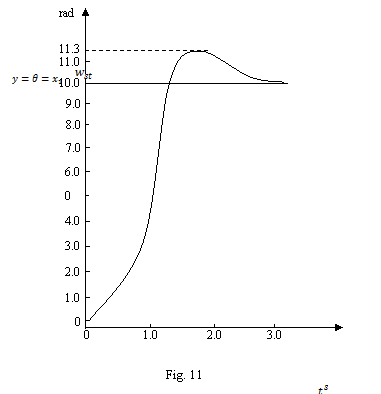Determinarea
solutiilor optime cu functii criteriu in limbaj intrare-stare-iesire, cu timp
final impus
1. Determinarea solutiei optime in conformitate cu
functia criteriu 
Se poate arata [14] ca in cazul cand se
foloseste pentru sistemul (4.10) functia criteriu  din (2.8),
cu timp final
din (2.8),
cu timp final  impus,
comanda optimala - de tipul (4.17) - are expresia
impus,
comanda optimala - de tipul (4.17) - are expresia
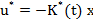 , (1)
, (1)
matricea  a
parametrilor optimi ai regulatorului avand elemente care sunt functii de timp,
spre deosebire de matricea
a
parametrilor optimi ai regulatorului avand elemente care sunt functii de timp,
spre deosebire de matricea 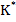 din (4.17),
ale carei elemente sunt constante.
din (4.17),
ale carei elemente sunt constante.
Matricea  are o
expresie analoaga cu (4.45), respectiv
are o
expresie analoaga cu (4.45), respectiv
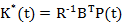 (2)
(2)
dar P(t) nu mai
are elemente constante, ci are elemente cu functii de timp, intrucat P(t)
reprezinta solutia ecuatiei matriceale diferentiale Riccati
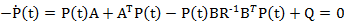 (3)
(3)
- unde 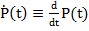 - cu
conditia finala [14]:
- cu
conditia finala [14]:
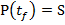 (4)
(4)
Solutia optima (2) pentru parametrii
regulatorului nu mai este deci o solutie stationara - ca in (4.45) - si ca
urmare ofera un program de variatie in timp a parametrilor respectivi,
realizarea acestui program asigurand minimizarea criteriului 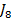
Rezolvarea ecuatiei (3) este prezentata
in [14].
Daca  , atunci criteriul
, atunci criteriul 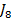 tinde catre
criteriul
tinde catre
criteriul 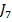 - avand in
vedere si (4.15) - si elementele matricei P(t) devin constante, deci
- avand in
vedere si (4.15) - si elementele matricei P(t) devin constante, deci
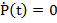
si ecuatia
diferentiala (3) devine ecuatia algebrica (4.43)
2. Determinarea unei solutii suboptimale prin
intermediu criteriului 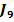
In
[15] este folosita metoda gradientului conjugat pentru obtinerea unei solutii
suboptimale in cazul unui bloc F descris de ecuatii de stare de forma
 (5)
(5)
si al adoptarii criteriului 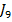 din (2.9).
din (2.9).
Solutia este suboptimala - sau aproximativ optimala - deoarece in cazul
cautarii valorilor optime ale unor parametrii ai regulatorului conduce la valori
constante ale acestor parametrii si nu la valori variabile in timp dupa un
anumit program, cum a rezultat in paragraful anterior.
Solutia suboptimala poate fi
cautata in spatiul unor functii continue sau in spatiul unor parametri; in
primul caz apare dificultatea ca spatiul nu este complet, in timp ce in al
doilea caz rezulta un spatiu Hilbert 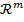 (m fiind numarul parametrilor
regulatorului), care este complet.
(m fiind numarul parametrilor
regulatorului), care este complet.
Metoda poate fi aplicata si
pentru regulatoare instalate pe calea directa.
In continuare, utilizarea
metodei gradientului conjugat pentru minimizarea unor criterii de tipul 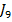 este
ilustrata prin intermediul algoritmului si a doua exemple din [15] (fara a
prezenta demonstratiile care fundamenteaza etapele de calcul), in primul caz
cautarea fiind efectuata in spatiul U al unor functii continue, iar in al doilea caz in
spatiul Hilbert
este
ilustrata prin intermediul algoritmului si a doua exemple din [15] (fara a
prezenta demonstratiile care fundamenteaza etapele de calcul), in primul caz
cautarea fiind efectuata in spatiul U al unor functii continue, iar in al doilea caz in
spatiul Hilbert 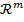 al
parametrilor regulatorului.
al
parametrilor regulatorului.
1. Algoritmul
utilizat
Metoda gradientului conjugat
(expusa in paragraful 1.4.4) realizeaza cautarea minimului unei functii
criteriu F(x) - x luand valori
intr-un anumit spatiu X ,
deci 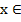 X prin intermediul urmatorului algoritm:
X prin intermediul urmatorului algoritm:
a) Se alege o valoare initiala
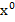
b) Se adopta ca directie
initiala de cautare
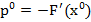 (6)
(6)
unde 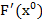 este
gradientul functiei criteriu F in
punctul
este
gradientul functiei criteriu F in
punctul 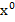 ; daca se noteaza (pentru prescurtarea scrierii
relatiilor)
; daca se noteaza (pentru prescurtarea scrierii
relatiilor)
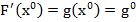 (7)
(7)
atunci relatia (6) capata forma
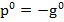 (8)
(8)
c) Se determina valoarea
urmatoare 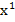 a secventei
de cautare prin relatia generala
a secventei
de cautare prin relatia generala
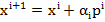 (9)
(9)
- identica cu (1.106) - relatie care pentru i = 0 devine
 ; (10)
; (10)
in (10) valorile 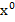 si
si 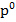 sunt
cunoscute de la punctele a) si b) , iar pentru
sunt
cunoscute de la punctele a) si b) , iar pentru 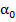 se adopta
valoarea care minimizeaza expresia
se adopta
valoarea care minimizeaza expresia
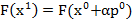 (11)
(11)
In general, valoarea 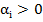 se
determina din conditia minimizarii expresiei
se
determina din conditia minimizarii expresiei
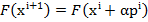 (12)
(12)
minimizare efectuata in raport cu variabila scalara pozitiva 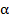 , deci efectuata de-a lungul unei drepte (vezi
paragraful 1.4.5).
, deci efectuata de-a lungul unei drepte (vezi
paragraful 1.4.5).
d) Se calculeaza gradientul 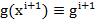 in punctul
in punctul 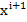 (deci,
pentru i = 0, se calculeaza
gradientul
(deci,
pentru i = 0, se calculeaza
gradientul 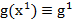 in punctul
in punctul 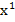
e) Se stabileste noua directie
de cautare 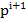 , din punctul
, din punctul 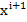 , conform relatiei
, conform relatiei
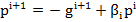 (13)
(13)
cu
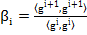 (14)
(14)
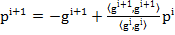 (15)
(15)
relatie identica cu (1.161).
Pentru i = 0, expresia (15) devine
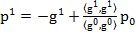 (16)
(16)
valorile 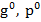 si
si 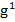 fiind
cunoscute de la punctele b) si d).
fiind
cunoscute de la punctele b) si d).
f) Se continua cu determinarea
noului punct  al
secventei de cautare prin intermediul relatiei (10) si (16), iar
al
secventei de cautare prin intermediul relatiei (10) si (16), iar 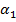 fiind
determinat ca la punctul c).
fiind
determinat ca la punctul c).
g) Se calculeaza 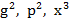 etc.
etc.
h) Secventa de cautare se
incheie atunci cand nu mai poate fi gasita o valoare 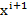 care sa
asigure conditia
care sa
asigure conditia
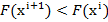 (17)
(17)
deci cand minimul a fost atins, fapt indicat si de anularea gradientului in
punctul de minim 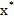
In cazul aplicarii algoritmului
descris pentru minimizarea functiei criteriu 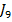 din (2.9)
din (2.9)
rezultand deci 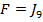 , functionala F
fiind criteriul
, functionala F
fiind criteriul 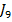 - apar doua
probleme, datorita specificului criteriului
- apar doua
probleme, datorita specificului criteriului 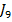 : prima
problema se refera la evaloarea valorilor functiei criteriu
: prima
problema se refera la evaloarea valorilor functiei criteriu 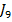 , iar a doua se refera la determinarea
gradientului functiei criteriu.
, iar a doua se refera la determinarea
gradientului functiei criteriu.
Intrucat apar aspecte
intrucatva diferite in cazul cautarii minimului in spatiul U al unor functii continue si in spatiul 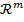 al
parametrilor regulatorului, in continuare problemele mentionate sunt prezentate
separat pentru fiecare din cele doua cazuri.
al
parametrilor regulatorului, in continuare problemele mentionate sunt prezentate
separat pentru fiecare din cele doua cazuri.
 2. Cautarea minimului in spatiul unor functii continue
2. Cautarea minimului in spatiul unor functii continue
In acest caz blocul BF (fig. 4) este descris de ecuatiile de stare
x = f(x, 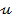 (18)
(18)
si se cauta comanda optima 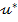 care sa
asigure o anumita variatie datorita
care sa
asigure o anumita variatie datorita 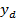 pentru
marimea de iesire y, criteriul
adoptat fiind
pentru
marimea de iesire y, criteriul
adoptat fiind 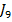
Intrucat comanda  reprezinta
o functie continua de timp (in cazul instalatiilor tehnologice multivariabile,
u este o marime vectoriala ale carei componente sunt functii continuale de
timp), expresia optima
reprezinta
o functie continua de timp (in cazul instalatiilor tehnologice multivariabile,
u este o marime vectoriala ale carei componente sunt functii continuale de
timp), expresia optima 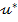 - care
minimizeaza criteriul
- care
minimizeaza criteriul 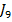 - este
cautata in spatiul U al
unor functii continue.
- este
cautata in spatiul U al
unor functii continue.
Folosind notatia
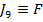
se poate
arata [15] ca functionala F(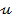 ) este un operator compus.
Astfel, dupa cum se vede in figura 5, functia f din (18) realizeaza o prima
transformare a marimilor
) este un operator compus.
Astfel, dupa cum se vede in figura 5, functia f din (18) realizeaza o prima
transformare a marimilor  (din spatiul U)
in marimile
(din spatiul U)
in marimile 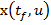 (din spatiul Hilbert
(din spatiul Hilbert 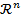 , n fiind dimensiunea vectorului de stare x); prin integrarea
ecuatiilor de stare (18) intre
, n fiind dimensiunea vectorului de stare x); prin integrarea
ecuatiilor de stare (18) intre  si
si  - limitele de integrare la
- limitele de integrare la 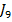 - cu conditia initiala.
- cu conditia initiala.
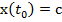 (19)
(19)
(reprezentand
un vector cu componete constante) se obtine in 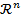 pentru fiecare comanda
pentru fiecare comanda 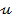 din U
un anumit vector
din U
un anumit vector 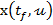 , reprezentand starea finara
corespunzatoare comenzii respective u.
, reprezentand starea finara
corespunzatoare comenzii respective u.
Fiecarei stari finale 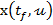 din
din 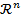 - aferente
unei anumite comenzi din U - ii
va corespunde - prin intermediul unei functionale
- aferente
unei anumite comenzi din U - ii
va corespunde - prin intermediul unei functionale 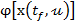 (fig. 5) -
o anumita valoare in
(fig. 5) -
o anumita valoare in 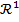 a criteriului
a criteriului
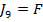 ; rezulta astfel ca prin compunerea celor doua
transformari f (din U in
; rezulta astfel ca prin compunerea celor doua
transformari f (din U in 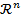 ) si
) si 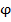 din (
din (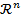 in
in 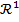 ) se obtine de fapt transformarea
) se obtine de fapt transformarea 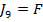 (din U in
(din U in 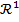
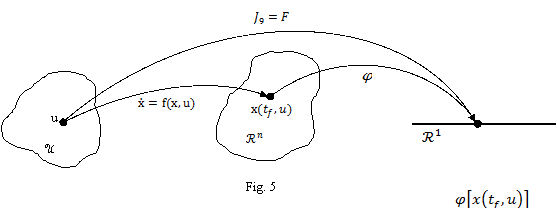
* De remarcat ca in (18) x reprezinta starea, iar comanda 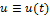 din spatiul U corespunde marimii
din spatiul U corespunde marimii 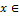 X din
cadrul algoritmului de la punctul 1 al prezentului paragraf.
X din
cadrul algoritmului de la punctul 1 al prezentului paragraf.
Din figura 5 se constata astfel
ca are loc relatia
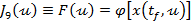 (20)
(20)
Pentru obtinerea gradientului 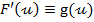 - al
functionalei
- al
functionalei  , corespunzator unei anumite comenzi
, corespunzator unei anumite comenzi 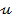 - in [15]
se recomanda metodologie (pentru
- in [15]
se recomanda metodologie (pentru 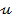 scalar,
scalar, 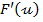 este tot scalar):
este tot scalar):
a) Se integreaza, pentru o
anumita comanda  ecuatia (18),
de la
ecuatia (18),
de la  la
la  - cu
conditia initiala (19) - si se determina variatia starii x in intervalul [
- cu
conditia initiala (19) - si se determina variatia starii x in intervalul [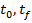 ], precum si starea finala x(
], precum si starea finala x(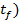 corespunzatoare comenzii respective
corespunzatoare comenzii respective 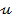
b) din (18) se calculeaza
derivatele partiale
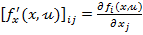 , i,j = 1,
2, .. , n (21
a)
, i,j = 1,
2, .. , n (21
a)
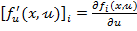 , i = 1,
2, .. , n (21 b)
, i = 1,
2, .. , n (21 b)
unde  este
componenta i a functiei vectoriale
este
componenta i a functiei vectoriale 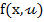 din (5).
din (5).
c) Se formeaza sistemul adjunct de ecuatii
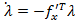 (22)
(22)
unde 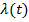 este o
variabila vectoriala;
este o
variabila vectoriala;
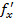 - matricea
- matricea  ale carei
elemente sunt
ale carei
elemente sunt 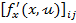 din (21 a).
din (21 a).
d) Se evalueaza valoarea  la momentul
final
la momentul
final  prin
intermediul relatiei
prin
intermediul relatiei
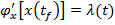 (23)
(23)
unde 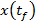 a fost
obtinut de la punctul a), iar
a fost
obtinut de la punctul a), iar
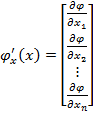 (24)
(24)
reprezinta gradientul functiei 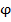 din (20).
din (20).
e) Avand  din (23) se
integreaza sistemul adjunct (22) inapoi in timp de la
din (23) se
integreaza sistemul adjunct (22) inapoi in timp de la  la
la  , rezultand evolutia variabilei vectoriale
, rezultand evolutia variabilei vectoriale  in intervalul
in intervalul
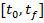
f) Se obtine gradientul cautat 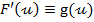 - pentru
functia de comanda
- pentru
functia de comanda  considerata
la punctul a) - prin intermediul relatiei
considerata
la punctul a) - prin intermediul relatiei
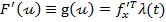 (25)
(25)
unde 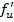 este
functia vectoriala ale carei componente sunt
este
functia vectoriala ale carei componente sunt 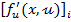 din (21 b).
din (21 b).
Gradientul obtinut  poate fi
utilizat in cadrul cautarii optimalului prin algoritmul expus la punctul 1.
poate fi
utilizat in cadrul cautarii optimalului prin algoritmul expus la punctul 1.
Integrarea ecuatiilor (18) si (22)
se efectueaza cu calculator numeric prin intermediul matricei de tranzitie [15,
16, 17].
Optimizarea realizata pe
aceasta cale este o optimizare in circuit deschis, intrucat comanda optimala 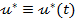 este
obtinuta numai prin calcul, fara a depinde de variatia unor marimi masurate
(cum este cazul optimizarii in circuit inchis, cand comanda optimala se obtine
direct prin intermediul unor marimi masurate - cum sunt variabilele de stare -
si transmise regulatorului functie de stare).
este
obtinuta numai prin calcul, fara a depinde de variatia unor marimi masurate
(cum este cazul optimizarii in circuit inchis, cand comanda optimala se obtine
direct prin intermediul unor marimi masurate - cum sunt variabilele de stare -
si transmise regulatorului functie de stare).
Totodata, optimizarea
respectiva este o optimizare care poate fi transpusa in practica numai prin
interventia operatorului uman ("off-line") - deci nu este o optimizare
realizata prin fluxul semnalelor transmise de echipamentele de automatizare
("on-line") - deoarece comanda optimala 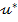 va trebui
realizata in practica prin interventia operatorului, dupa incheierea
determinarii pe calculator a acestei comenzi.
va trebui
realizata in practica prin interventia operatorului, dupa incheierea
determinarii pe calculator a acestei comenzi.
La punctul 4 este prezentat un
exemplu de optimizare de acest tip, cu cautarea minimului in spatiul unor
functii continue, fiind ilustarte determinarea functiei φ si obtinerea gradientului 
3. Cautarea minimului in spatiul parametrilor regulatorului
In acest caz se presupune ca se
realizeaza o reglare functie de stare - instaland regulatorul pe reactii in
jurul blocului F, ca in figura 3 - si pentru un anumit semnal de referinta 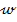 , aplicat la intrarea sistemului functionand in
circuit inchis, se cauta acele valori
, aplicat la intrarea sistemului functionand in
circuit inchis, se cauta acele valori 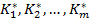 (ale
parametrilor regulatorului
(ale
parametrilor regulatorului 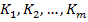 ) care minimizeaza un criteriu de forma
) care minimizeaza un criteriu de forma 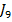 si deci
optimizeaza functionarea sistemului de reglare automata.
si deci
optimizeaza functionarea sistemului de reglare automata.
In practica se considera cazul
unui semnal treapta 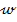 , intrucat optimizarea comportarii la semnale
treapta asigura o buna comportare si la alte tipuri de semnale.
, intrucat optimizarea comportarii la semnale
treapta asigura o buna comportare si la alte tipuri de semnale.
Ecuatiile de stare pot fi puse
in acest caz sub forma
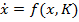 (26)
(26)
- unde
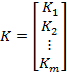 (27)
(27)
- functia vectoriala fiind explicita in raport cu parametri 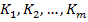 si neteda
in raport cu x si K; vectorul parametrilor K ar putea fi notat si prin u.
si neteda
in raport cu x si K; vectorul parametrilor K ar putea fi notat si prin u.
Intrucat un parametru al
regulatorului, de exemplu 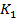 , poate fi considerat ca o functie de comanda care
are o valoare constanta, cele mai multe din considerentele de la punctul 2
raman valabile pentru determinarea gradientului functionalei, necesar aplicarii
metodei gradientului conjugat.
, poate fi considerat ca o functie de comanda care
are o valoare constanta, cele mai multe din considerentele de la punctul 2
raman valabile pentru determinarea gradientului functionalei, necesar aplicarii
metodei gradientului conjugat.
Deosebirea care apare fata de
metodologia de la punctul 2 - si care se datoreste faptului ca de data aceasta
minimul este cautat in spatiul Hilbert 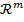 al
parametrilor regulatorului, in loc de a fi cautat in spatiul unor functii
continue - consta in faptul ca in locul relatiei (25) pentru obtinerea
gradientului se foloseste expresia
al
parametrilor regulatorului, in loc de a fi cautat in spatiul unor functii
continue - consta in faptul ca in locul relatiei (25) pentru obtinerea
gradientului se foloseste expresia
 (28)
(28)
unde 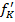 este o
matrice n × m, ale carei elemente sunt definite de relatiile
este o
matrice n × m, ale carei elemente sunt definite de relatiile
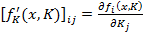 (29)
(29)
(cu 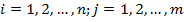 ), iar
), iar  reprezinta
solutia sistemului adjunct (22).
reprezinta
solutia sistemului adjunct (22).
Optimizarea realizata pe
aceasta cale este o optimizare in circuit inchis, intrucat sistemul de reglare
functie de stare functioneaza in bucla inchisa. Totodata, optimizarea
respectiva este de tipul "off-line", intrucat valorile optimie ale parametrilor
regulatorului - formand vectorul 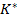 - sunt
determinate pe calculator si apoi fixate practic prin interfventia operatorului
uman.
- sunt
determinate pe calculator si apoi fixate practic prin interfventia operatorului
uman.
La punctul 5 este prezentat un
exemplu de optimizare cu cautarea minimului in spatiul parametrilor
regulatorului.
4. Exemplu de cautare a minimului in spatiul unor functii continue
Pentru ilustrare este
considerat motorul de curent continuu din [15], comandat prin circuitul de
excitatie (fig. 6), si alimentat cu un curent i in circuitul indusului de la o sursa independenta.
Motorul este caracterizata de
rezistenta 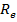 si
inductivitatea
si
inductivitatea 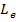 in
circuitul de excitatie, de la momentul de inertie echivalent J si de coeficientul de frecari vascoase
D; la bornele circuitului de
excitatie se aplica tensiunea de comanda u,
prin circuitul respectiv circuland curentul
in
circuitul de excitatie, de la momentul de inertie echivalent J si de coeficientul de frecari vascoase
D; la bornele circuitului de
excitatie se aplica tensiunea de comanda u,
prin circuitul respectiv circuland curentul 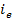
Notand cu θ pozitia unghiulara a arborelui
(reprezentand marimea de iesire y a
motorului) cu 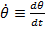 viteza
unghiulara si cu
viteza
unghiulara si cu 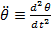 acceleratia
unghiulara, ecuatiile motorului - in ipoteza liniarizarii in jurul unui punct
de functionare - au aspectul
acceleratia
unghiulara, ecuatiile motorului - in ipoteza liniarizarii in jurul unui punct
de functionare - au aspectul
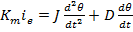 (30)
(30)
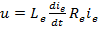 (31)
(31)
Alegand variabilele de stare
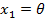 (32)
(32)
 (33)
(33)
 (34)
(34)
din (30) . (34) se obtin ecuatiile de stare
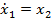 (35)
(35)
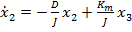 (36)
(36)
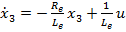 (37)
(37)
Introducand valori numerice
(corespunzatoare parametrilor unui motor
de 5 CP) pentru D, J, 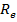
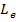
 in [15] se
obtin ecuatiile de stare sub forma
in [15] se
obtin ecuatiile de stare sub forma
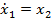 (38)
(38)
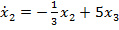 (39)
(39)
 (40)
(40)
deci sub
forma cunoscuta
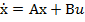
Folosind amplificatoare
operationale integratoare, sumatoare si multiplicatoare cu o constanta,
ecuatiile (38) . (40) conduc la schema echivalenta a motorului din
figura 7, care poate fi simulata pe calculator analogic.
Optimizarea isi propune sa
gaseasca acea comanda 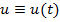 care sa
asigure o variatie cat mai apropiata de o treapta - de la 0 la 10 radiani - a
pozitiei unghiulare
care sa
asigure o variatie cat mai apropiata de o treapta - de la 0 la 10 radiani - a
pozitiei unghiulare 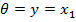 In acest scop se alege un criteriu de forma
In acest scop se alege un criteriu de forma 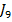 cu
cu
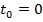 (41)
(41)
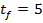 secunde, (42)
secunde, (42)
si
 (43)
(43)
considerand ca in momentul initial 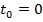 motorul se
gaseste in repaus.
motorul se
gaseste in repaus.
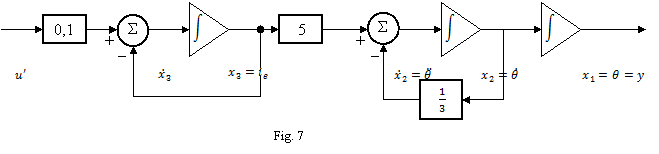
Intrucat 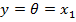 si u sunt marimi scalare, primul termen al
criteriului
si u sunt marimi scalare, primul termen al
criteriului 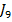 din (2.9)
capata forma
din (2.9)
capata forma
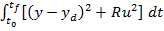 (44)
(44)
adoptand
factorul de ponderare 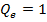 .
.
Intrucat
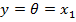
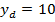 radiani
radiani
se obtine pentru (44) expresia
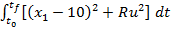 (45)
(45)
Avand
in vedere (32) . (34) si faptul ca in noul regim stationar motorul
trebuie sa se gaseasca in repaus (cu 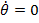 si
si  ) si cu o pozitie unghiulara
) si cu o pozitie unghiulara 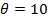 radiani,
rezulta ca valorile dorite pentru variabilele de stare la intrarea in noul
regim stationar sunt.
radiani,
rezulta ca valorile dorite pentru variabilele de stare la intrarea in noul
regim stationar sunt.
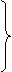
 radiani
radiani
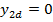 (46)
(46)
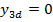
Adoptand matricea de ponderare S - din (2.9) - diagonala, respectiv
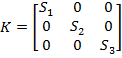 (47)
(47)
termenul
al doilea din (2.9) va avea expresia
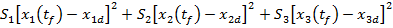
si introducand valorile din (46) se
obtine
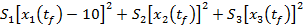 (48)
(48)
Avand
in vedere notatia 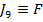 (de la
punctul 2), din (45) si (48) rezulta expresia
(de la
punctul 2), din (45) si (48) rezulta expresia
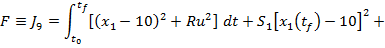
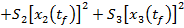 (49)
(49)
care se poate scrie si sub forma
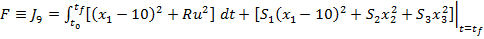 (50)
(50)
Tinand
cont de forma criteriului 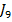 din (50) , sistemul
ecuatiilor de stare (38) . (40) se extinde cu ecuatia suplimentara
din (50) , sistemul
ecuatiilor de stare (38) . (40) se extinde cu ecuatia suplimentara
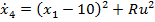 (51)
(51)
variabila 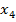 fiind
definita astfel incat sa satisfaca (51) si conditia initiala
fiind
definita astfel incat sa satisfaca (51) si conditia initiala
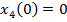 (52)
(52)
Avand
in vedere (51) , functia criteriu (50) capata
forma
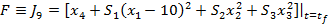 (53)
(53)
dar, conform cu (20), aceasta este expresia functiei 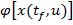 care
asigura transformarea din figura
care
asigura transformarea din figura
Intrucat comanda u este
inclusa in variabila 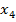 , conform cu (51) , se poate scrie
, conform cu (51) , se poate scrie
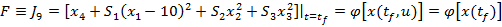 (54)
(54)
Sistemul (38) . (40) , extins cu (51) , determina aspectul ecuatiilor (18) sub
forma
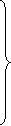
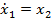
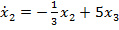


cu conditia initiala
 (56)
(56)
avand in vedere (43) si (52) .
Aplicand (21) si (22) la sistemul (55) se
obtin expresiile:
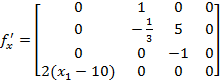 (57)
(57)
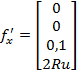 (58)
(58)
Introducand (57) in (22) se obtine ecuatia sistemului adjunct
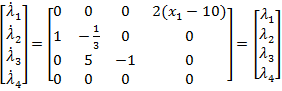 (59)
(59)
Din (54) se
obtine
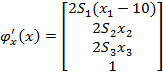 (60)
(60)
avand in
vedere (24).
Introducand
(58) in (25) rezulta
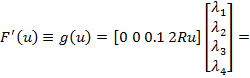
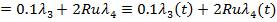 (61)
(61)
Conform celor mentionate la punctul 2, a,
se integreaza sistemul (55) pentru o anumita functie de comanda u si se determina evolutia starii x de
la 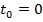 la
la  ; introducand in (60) valoarea x(
; introducand in (60) valoarea x(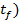 se obtine
se obtine
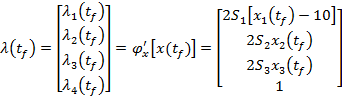 (62)
(62)
conform cu (23).
Valoarea  din (62) reprezinta conditia terminala pentru
integrarea de la
din (62) reprezinta conditia terminala pentru
integrarea de la  la
la  a
sistemului adjunct (59) , ceea ce
permite obtinerea evolutiei
a
sistemului adjunct (59) , ceea ce
permite obtinerea evolutiei 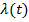 si deci a
gradientului
si deci a
gradientului 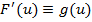 prin
intermediul relatiei (61) .
prin
intermediul relatiei (61) .
In
[15] calculele mentionate au fost efectuate cu 
 in (49) , adoptand pentru prima iteratie functia de
comanda
in (49) , adoptand pentru prima iteratie functia de
comanda  . Dupa 10 iteratii s-a obtinut o valoare suficient
de redusa a normei gradientului, procesul de cautare a minimului functiei
criteriu fiind considerat incheiat.
. Dupa 10 iteratii s-a obtinut o valoare suficient
de redusa a normei gradientului, procesul de cautare a minimului functiei
criteriu fiind considerat incheiat.
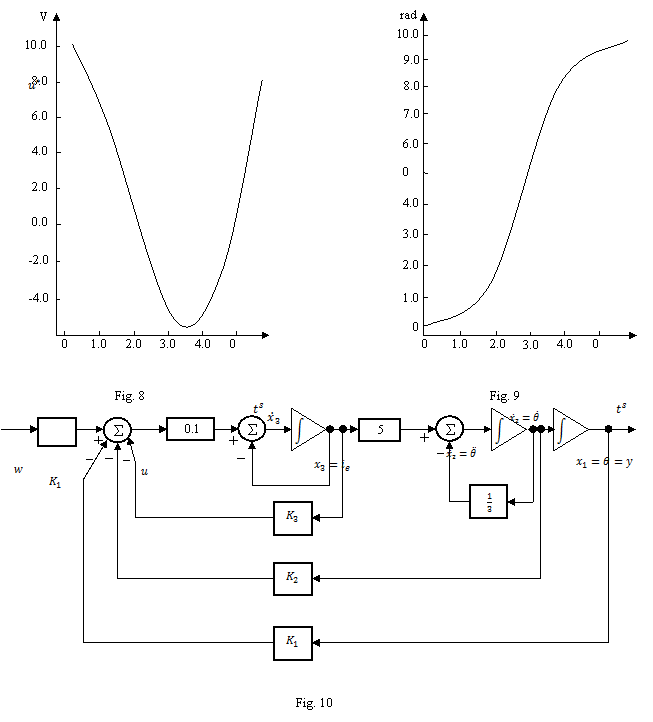
Aspectul comenzii optime 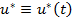 , obtinut dupa 10 iteratii, este reprezentat in
figura 8, iar variatia corespunzatoare a pozitiei unghiulare θ a arborelui (reprezentand marimea de
iesire) - ca raspuns la comanda
, obtinut dupa 10 iteratii, este reprezentat in
figura 8, iar variatia corespunzatoare a pozitiei unghiulare θ a arborelui (reprezentand marimea de
iesire) - ca raspuns la comanda 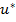 din figura 8
- este reprezentata in figura 9; din aceasta se constata ca trecerea marimii
din figura 8
- este reprezentata in figura 9; din aceasta se constata ca trecerea marimii 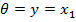 de la 0 la
10 radiani aproximeaza destul de bine o variatie treapta.
de la 0 la
10 radiani aproximeaza destul de bine o variatie treapta.
Exemplu
de cautare a minimului in spatiul parametrilor regulatorului
Pentru
motorul din exemplul de la punctul 4 se realizeaza o reglare functie de stare,
folosind blocurile cu factorii de proportionalitate 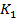
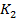
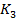 (reprezentand parametrii regulatorului) care inmultesc
marimile de stare
(reprezentand parametrii regulatorului) care inmultesc
marimile de stare 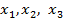 (fig. 10).
(fig. 10).
variabilele de stare fiind acelasi ca in (32) . (34) ; se constata ca expresiile (49) si (63) sunt analoage, in locul
valorii de 10 radiani intervenind valoarea 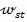 , care reprezinta valoarea dorita pentru marimea
de iesire
, care reprezinta valoarea dorita pentru marimea
de iesire 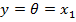
Ca
urmare, ecuatiile de stare extinse sunt analoage cu (55) , insa fata de cazul din exemplul anterior,
de la punctul 4, intervine relatia
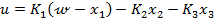 (64)
(64)
care corespunde functionarii sumatorului de la
intrarea sistemului.
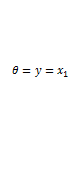
Pentru
o variatie treapta a marimii de referinta - de la 0 la valoarea stationara constanta
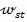 - se cauta
valorile optime
- se cauta
valorile optime 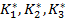 care
asigura minimizarea functiei criteriu
care
asigura minimizarea functiei criteriu
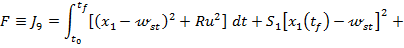
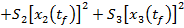 (63)
(63)
Ecuatiile (55) si (64) formeaza sistemul (26), cu
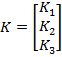 (65)
(65)
Folosind metodologia de la punctul 3 in [15] au fost adoptate pentru (63) valorile R = 0.001, 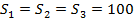
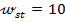
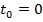
 s,
s,  si valorile
pentru prima iteratie
si valorile
pentru prima iteratie 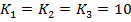 , rezultand dupa 22 iteratii parametrii optimi
, rezultand dupa 22 iteratii parametrii optimi
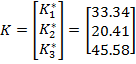
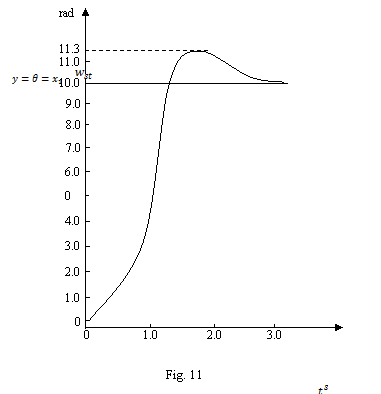
si raspunsul y al sistemului de reglare (la variatia
treapta a marimii de referinta 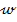 de la 0 la 10 radiani)
din figura 11, considerandu-se un suprareglaj de circa 11.3 %. de la 0 la 10 radiani)
din figura 11, considerandu-se un suprareglaj de circa 11.3 %.
Prin asigurarea unei saturatii care liminteaza
comanda in gama 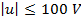 , se obtine o reducere sensibila a
suprareglajului [15]. Aceasta limitare determina un
caracter neliniar al sistemului. , se obtine o reducere sensibila a
suprareglajului [15]. Aceasta limitare determina un
caracter neliniar al sistemului.
|
|


 ; (10)
; (10)
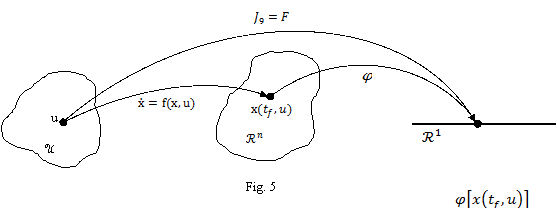
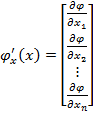 (24)
(24)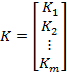 (27)
(27)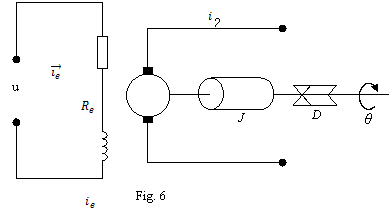
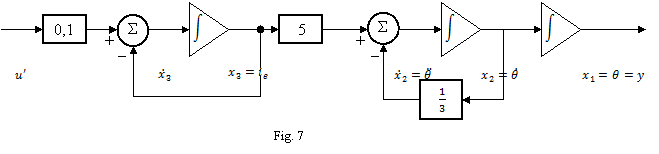
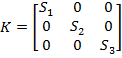 (47)
(47) 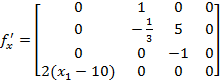
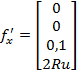
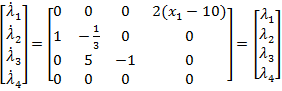 (59)
(59) 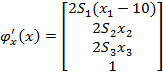
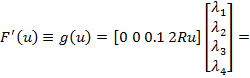
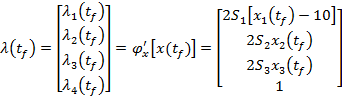 (62)
(62) 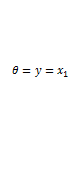

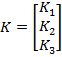 (65)
(65)