Efectul piezoelectric

Efectul piezoelectric

Proprietatea deosebita a unor materiale feroelectrice este piezoelectricitatea sau efectul piezoelectric.

Efectul piezoelectric a fost descoperit in anul 1880 de catre fratii Pierre si Jacque Curie si pus in evidenta prin aparitia unei diferente de potential electric la capetele unui dielectric sau feroelectric, atunci cand asupra lui actioneaza o forta de compresie mecanica. Diferenta de potential se datoreaza polarizarii electrice a materialului piezoelectric sub actiunea deformatoare a solicitarii mecanice externe. Polarizarea electrica consta in aparitia unor sarcini electrice pe suprafata materialelor piezoelectrice supuse actiunii fortelor de compresie sau de intindere.

Materialele monocristaline sau policristaline supuse actiunii unei presiuni mecanice genereaza o tensiune electrica, acesta este efectul piezoelectric direct, iar sub actiunea unui camp electric sufera o deformare mecanica (distorsiune mecanica numita electrostrictiune) acesta corespunde efectului piezoelectric indirect.

Piezoelectricitatea este caracterizata printr-o relatie directa intre cauza si

efect.

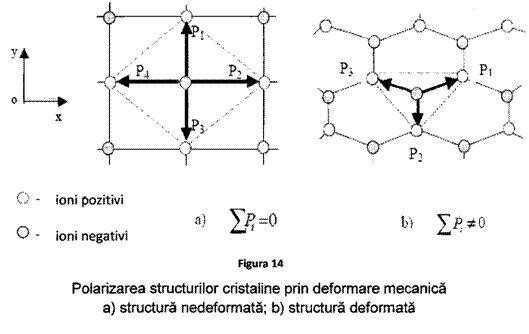
Pentru structurile cristaline reprezentate bidimensional in planul xOy (fig.13.a.), lipsa actiunii mecanice exterioare, pune in evidenta polarizarea rezultanta cu valoare nula ca urmare a structurii simetrice a cristalului.

In cazul in care se actioneaza din exterior asupra cristalului, are loc deformarea structurii interne a retelei (fig.13.), ionii se deplaseaza, polarizare interna nu mai este in echilibru si are loc polarizarea cristalului prin efect direct, deci polarizarea rezultanta este diferita de zero.

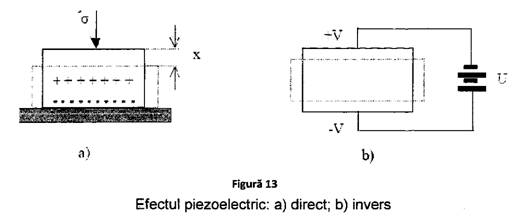
In figura 13. efectul de polarizare este pus in evidenta prin momentul dipolar al celulelor unitare, moment incadrat cu linie punctata.

Polarizarea P, indusa in materialul cristalin, este direct proportionala cu solicitarea (presiunea) mecanica aplicata din exterior conform relatiei (17), care reprezinta expresia efectului piezoelectric direct.

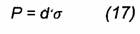
unde: tensiunea mecanica σ se defineste ca forta aplicata pe unitatea de suprafata σ F/S.

Factorul de proportionalitate d dintre polarizarea P si solicitarea mecanica σ a fost denumit piezomodul, a carui valoare depinde de natura materialului piezoelectric.

Fenomenul piezoelectric are si un efect invers prin aceea ca asigurarea unei polarizari electrice a materialului cristalin determina la acesta o deformare elastica x. Deformarea x este direct proportionala cu polarizarea P prin intermediul unui coeficient piezoelectric g, conform relatiei.

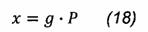
In baza relatiei de legatura (6.3.) dintre polarizare si campul electric care il determina, expresia efectului piezoelectric invers este determinata prin relatia (20).

P = -1)E   

Din relatia (20) rezulta expresia piezomodulului d, care depinde de marimea coeficientului piezoelectric g , permitivitatea electrica absoluta a vidului si permitivitatea electrica a materialului piezoelectric (care depinde de permitivitatea electrica relativa a materialului piezoelectric prin relatia: =

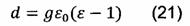
Relatiile (6.1.) si (6.4.) referitoare la efectul piezoelectric direct si invers exprimate in planul bidimensional pot fi generalizate pentru spatiul tridimensional conform relatiilor (6.6.) si (6.7.), care evidentiaza efectul piezoelectric direct si respectiv efectul piezoelectric invers.

unde:i=1,2,3 corespunzator celor trei polarizari dupa axele de coordonate;

j = 1, 2, 6 corespunzator eforturilor normale si tangentiale la suprafetele perpendiculare pe axele de coordonate.

Pot fi definite si ecuatiile pentru determinarea campului electric E si tensiunii mecanice σ pentru cazul in care se cunoaste polarizarea electrica P si deformarea elastica x. De obicei, se considera E si σ ca variabile independente. Se aplica un camp electric E si o tensiune mecanica  σ si se masoara polarizarea P si deformarea x.

Materialele piezoelectrice cunoscute si utilizate frecvent sunt de natura monocristalina sau de natura policristalina ( structura materialelor policristaline este prezentata in paragraful 6.2.).

Pentru materialele monocristaline (fig. 15 si fig. 16) axele sistemului ortogonal sunt denumite:

Ox-axa electrica (trece prin ionii retelei cristaline); Oy - axa mecanica; Oz - axa optica.

Monocristalele sunt de forma paralelipipedica cu fetele perpendiculare pe cele trei directii principale. Din acestea se taie mici paralelipipede (fig.15) cu unghiuri de inclinare diferite fata de axele sistemului ortogonal, in functie de frecventa de oscilatie electromecanica la care va lucra dispozitivul piezoceramic.

Pe fiecare suprafata a micilor paralelipipede (lamele) obtinute prin taiere, se definesc polarizarile Px, Py, Pz , polarizari care apar in urma solicitarilor mecanice (σx, σy, σz si ζx, ζy, ζz ) la care este supus monocristalul (fig.16).

O solicitare mecanica oarecare se poate defini intotdeauna ca rezultanta a sase componente de natura mecanica grupate astfel:

3 eforturi normale σx, σy, σz , avand ca unitate de masura [N/m];

3 eforturi de forfecare ζx, ζy, ζz, avand ca unitate de masura [N/m].