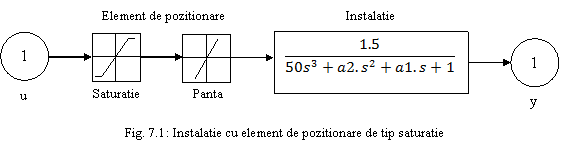Exemple cu functii
multiobiectiv in Matlab
Exemplele prezentate anterior rezolva
probleme cu o singura functie obiectiv. Acest paragraf prezinta rezolvarea
problemelor cu functii multiobiectiv, folosind programele lsqnonlin, fminimax, si fgoalattain. Vom prezenta intr-un
exemplu si cum se optimizeaza parametrii dintr-un model Simulink.
Exemple Simulink
Sa presupunem ca dorim sa optimizam
parametrii de conducere in modelul Simulink optsim.mdl
(acest model poate fi gasit in directorul pachetului de programe de optimizare;
notam ca Simulink trebuie instalat in sistem pentru a putea apela acest model).
Modelul contine o instalatie cu model neliniar ca in diagrama Simulink din
Figura 7.1.
Instalatia este un element de ordinul trei cu un element de pozitionare
neliniar. El contine o neliniaritate de tip saturatie si un element de limitare
a pantei de crestere. Elementul de tip saturatie "taie" intrarile mai mari de
doua unitati si mai mici de (-2) unitati. Limitatorul de panta are panta de 0.8
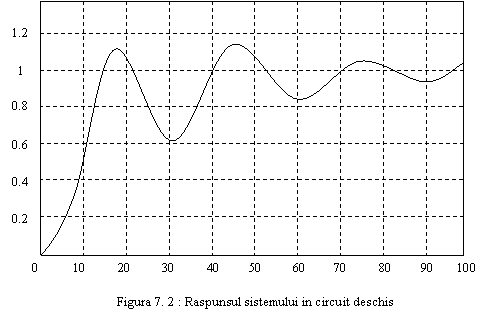
unitati/secunda. Raspunsul sistemului in circuit deschis la intrare - treapta
este aratat in Figura 7.2 (putem vizualiza raspunsul prin apelarea modelului
printr-o comanda a programului optsim,
apeland blocul Scope si ruland
simularea; raspunsul este trasat pe ecran)
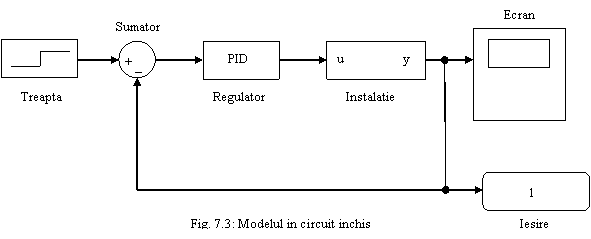
Problema este sa determinam o lege de reglare in circuit inchis pentru urmarirea
intrarii - treapta unitate aplicata la intrare. Sistemul in circuit inchis este
prezentat sub forma unei sheme-bloc
unde instalatia este plasata ca element condus. Pe display vor aparea
traiectoriile de iesire in timpul desfasurarii procesului (vezi Figura 7.3).
O cale de a rezolva aceasta problema este de a minimiza eroarea dintre
iesire si semnalul de la intrare.Variabilele sunt parametrii regulatorului PID.
Daca dorim sa minimizam eroarea numai pentru o unitate de timp (de exemplu 1
secunda), avem nevoie de o singura functie obiectiv. Dar scopul este sa minimizam
eroarea pentru toti pasii de la 0 la 100 secunde, ceea ce va necesita o functie
obiectiv multipla (o functie pentru fiecare pas).
Programul lsqnonlin este folosit
pentru a minimiza eroarea patratica a abaterii iesirii. Acest program este
definit in MATLAB prin fisierul tracklsq.m
aratat mai jos, care defineste semnalul de eroare. Semnalul eroare este yout, iesirea este calculata prin
apelarea functiei sim, minus semnalul
de intrare 1.
Functia tracklsq.m trebuie sa actioneze
simularea. Simularea poate fi actionata atat in spatiul de lucru de baza, cat
si in spatiul de lucru curent, adica in spatiul de lucru al functiei apelate sim, care in acest caz este spatiul de
lucru al functiei tracklsq.m. In
acest exemplu, comanda simset este
folosita pentru a anunta programul sim
sa actioneze simultan in spatiul curent de lucru punand "SrcWorkspace" la
"Current".
Pentru a actiona simularea in optsim
,trebuie definite variabilele kP, kI, kD, a1
si a2 (a1 si a2 sunt variabilele functiei de
transfer a instalatiei). KP, KI, si KD sunt
variabilele ce trebuie optimizate. Putem initializa a1 si a2
inainte de apelarea functiei lsqnonlin
si atunci vom trece cele doua variabile ca argumente aditionale. lsqnonlin va trimite a1 si a2
in tracklsq la fiecare pas, ceea ce
face ca cele doua sa nu mai poata fi folosite ca variabile globale.
Dupa alegerea unei rezolvari folosind functia simset, simularea functioneaza utilizand sim. Simularea este facuta folosind o metoda de ordinul cinci cu
pas fix pana la 100 secunde. Cand simularea este completa, variabilele tout, xuot si yout trec in spatiul
de lucru curent (adica in spatiul al functiei tracklsq). Blocul de iesire este folosit in shema-bloc pentru a transfera
yout in spatiul curent si a termina
simularea.
Pasul 1 : Deschide M-fisierul tracklsq.m
Functia F = tracklsq ( pid, a1,
a2 )
kp=pid(l); % muta variabilele intr - un model care nominalizeaza
parametrii
ki=pid(2);
kd=pid(3);
% alege rezolvarea si spatiul de lucru intr-o functie opt=simset (
'rezolvare', 'ode5', 'SrcWorkspace', 'current' );
[ tout, xout, yout ] = sim(
'option', [ 0, 100 ], opt );
F = yout - l % calculeaza eroarea
Pasul 2 : Apeleaza programul de optimizare
optsim % incarca modelul
pid0 = [ 0.63; 0.0504; 1.9688 ] % setul valorilor initiate
a1 = 3; a2 = 43 % initializeaza variabilele modelului
options = optimset ( 'LargeScale','off','display','iter','tolx','tolfur',
0.001)
pid = lsqnonlin ( 'tracklsq', pid0,
[], [], options, a1, a2 )
% pune variabilele din nou in spatiul
de lucru de baza
kp = pid(l); ki
= pid(2); kd = pid(3);
Variabilele optionale trecute in lsqlin
definesc criteriul si caracteristicile display-ului. In acest caz noi cerem
pentru iesire sa se utilizeze un algoritm de dimensiune medie si din toleranta
de terminare pentru pasi si pentru functia obiectiv sa fie de ordinul 0.001.
Optimizarea da solutia pentru factorii de proportionaliate (kp),
de integritate (ki) si derivativ (kd) ale regulatorului
dupa 73 de evaluari ale functiei:
Iteratia
|
Contorul de
evaluari ale
lui F
|
Reziduu
|
Pasul
|
Derivata
directionala
|
|
|
1
|
3
|
8.66531
|
1
|
-3.48
|
|
|
2
|
10
|
6.78831
|
1
|
-0.0634
|
3.4355
|
|
3
|
19
|
5.99204
|
5.5
|
-0.0446
|
0.28612
|
|
4
|
28
|
4.74992
|
5.78
|
-0.0213
|
0.0227966
|
|
5
|
36
|
4.51795
|
1.25
|
0.0222
|
0.0744258
|
|
6
|
43
|
4.5115
|
0.58
|
-0.00633
|
0.03445
|
|
7
|
51
|
4.49455
|
2.99
|
0.000688
|
0.017225
|
|
8
|
58
|
4.4836
|
0.915
|
0.00203
|
0.0180998
|
|
9
|
66
|
4.47724
|
1.22
|
0.000845
|
0.00904992
|
|
10
|
73
|
4.47405
|
0.801
|
-0.00072
|
0.0113409
|
Optimizarea se termina cu succes.
Gradientul pe directia de intrare
este mai mic decat tolFun=0.001
Gradientul este mai mic decat 10 *
( tolFun+tolX )
pid =
2.9107 0.1443 12.8161
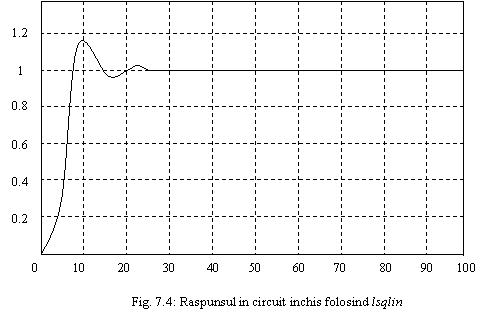
Raspunsul in circuit inchis rezultat este aratat in Figura 7.4:
Observatie:
Apelarea rutinei sim are ca
rezultat apelarea rezolvarii de catre pachetul de programe Simulink a unei ecuatii
diferentiale ordinare (EDO). Alegerea poate fi din punct de vedere al optimizarii,
o rezolare cu pas fixat este cea mai buna alegere daca ea este suficienta
pentru rezolvarea ecuatiei diferentiale ordinare. Totusi in cazul unui sistem
rigid, se poate apela o metoda cu pas variabil pentru rezolvarea ecuatiei
diferentiale ortiinare (EDO). Solutia numerica data de metoda de rezolvare cu
pas variabil, nu este, totusi, o functie neteda in raport cu parametrii,
datorita mecanismului de control al pasului. Aceasta lipsa a netezirii poate indeparta
programul de optimizare de convergenta finala. Lipsa netezirii nu se face simtita
cand se utilizeaza o metoda cu pas fixat.
Pachetul de programe NCD se recomanda pentru rezolvarea optimizarii
multiobiectiv in legatura cu aplicarea metodei cu pas variabil in Simulink;
asigura o metoda de gradient particulara care lucreaza in Simulink si evita
introducerea defectului de netezire.
O alta metoda de rezolvare este utilizarea functiei fminimax. In acest caz, pe langa minimizarea erorii intre semnalul
de iesire si cel de intrare, se minimizeaza si valoarea maxima (suprareglajul)
iesirii in fiecare moment intre 0 si 100.
Deci in functia trackmmobj, functia
obiectiv este iesirea returnata prin comanda sim. Dar minimizarea maximului iesirii (suprareglajul) la fiecare
pas al timpului intre 1 si 100, poate forta iesirea sa ramana mai mica intrarea
treapta unitate (=1) pentru un timp prea lung. Pentru a impune ca iesirea sa
atinga 0.95 dupa primele 20 de secunde, in functia trackmmcon, o functie care introduce restrictii, adaugam restrictia
yiesire ≥ 0.95 pentru t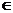
Deoarece restrictia trebuie pusa sub forma g ≤ 0, restrictia introdusa
in functie este: g = - yiesire ( 20, 100 ) + 0. 95.
Atat trackmmobj cat si trackmmcon foloseste rezultatul yiesire
dat de sim, calculat pentru
variabilele curente pid. Restrictia neliniara este intotdeauna chemata sa actioneze
asupra functiei obiectiv in fmincon, fminimax, fgoalattain si fseminf
care au lucrat cu aceleasi valori. Astfel vom evita solicitarea simularii de
doua ori, prin folosirea instructiunii assign
care acorda valoarea curenta a lui F ca variabila F - TRACKMMOBJ in spatiul de
lucru de baza. Atunci primul pas in trackmmcon
este sa utilizeze evalin pentru a
evalua variabila F - TRACKMMOBJ in spatiul de lucru de baza si, sa acorde
rezultatul lui F in trackmmcon.
Pasul 1 : Scrierea unui M-fisier trackmmobj.m pentru a calcula functia
obiectiv
Functia F = trackmmobj (pid, al, a2)
kp = pid(l);
ki = pid(2); % calculeaza valorile functiei
kd = pid(3);
opt = simset ( 'solver', 'ode5', 'ScrWorkspace', 'Current' );
[ tout, xout, yout ] = sim (
'option', [ 0, 100 ], opt) ;
F = yout
Assignin ( 'base', 'F -
TRACKMMOBJ', F )
Pasul 2 : Scierea unui M-fisier trackmmcon.m pentru a calcula restrictiile
neliniare
Function [ c, ceq ] = trackmmcon
(pid, a1, a2)
F = evalin ( 'base' , 'F - TRACKMMOBJ' );
% calculeaza restrictiile
c = - F [ 20; 100 ] + 0.95
ceq =[]
Notam ca fminimax va transfera a1
si a2 ca valori in functia obiectiv si in restrictii astfel ca trackmmcon cere argumentele la intrare
pentru aceste variabile chiar daca nu le va folosi.
Pasul 3 : Apelarea rutinei de optimizare cu
restrictii optisim
pid0 = [ 0.63, 0.0504, 1.9688 ]
a1 = 3 a2 = 43
options = optimset ( 'Display', 'iter',
'Tolx', 0.001, 'TolFun', 0.001 );
pid = fminimax ( 'trackmmobj';
pid0, [], [], [], [], [], [], 'trackmmcon', options, a1, a2
)
% transfera variabilele inapoi in spatiul de lucru de baza
kp = pid (l); ki = pid (2); kd = pid (3);
Rezulta:
Iteratia
|
Numarul
de evaluari
ale lui F
|
Max
|
Numar
de pasi
|
Derivata
directionala
|
Procedura
|
|
1
|
5
|
1.12
|
1
|
1.18
|
|
|
2
|
11
|
1.264
|
1
|
-0.172
|
|
|
3
|
17
|
1.055
|
1
|
-0.0128
|
Hessian modificata
de doua ori
|
|
4
|
23
|
1.004
|
1
|
3.49e-0.005
|
Hessian modificata
|
|
5
|
29
|
0.9997
|
1
|
-1.36e-0.006
|
Hessian modificata
|
Optimizarea s-a terminat cu succes
:
Directia de cautare este mai mica
decat 2 * options.tolx ( ≤ 2 * 0.001 ) si,
Maximul violarii restrictiei este
mai mica decat optiunea TolCon
pid =
0.5894 0.0605 5.5295
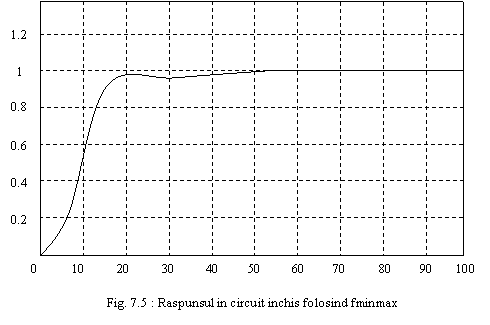
Ultima valoare aratata in coloana MAX arata ca valoarea
maxima la sfarsitul calculului este 0.9997. Raspunsul in circuit inchis cu
aceste rezultate este aratat in Figura 7. 5.
Aceasta solutie difera de cea obtinuta prin lsqlin deoarece problemele rezolvate sunt formulate diferit.
Exemplu de prelucrare a unui semnal
Consideram proiectia fazei-liniare a raspunsului finit filtrat (FIR).
Problema este sa determinam un filtru lowpas
cu amplitudinea 1 la toate frecventele intre 0 si 0.1 Hz si amplitudinea 0 intre
0.15 si 0.5 Hz. Raspunsul
frecventei H (f) pentru un astfel de filtru este definit de:
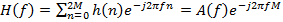 ( 1 -6 )
( 1 -6 )
Unde A(f) este amplitudinea frecventei. O solutie este sa aplicam o metoda a
atingerii tintei la amplitudinea frecventei. Fiind oferita o functie care
calculeaza amplitudinea, functia fgoalattain
va incerca sa varieze coeficientii a (n) ca raspuns ai amplitudinii pana cand raspunsul
amplitudinii se va potrivi cu raspunsul dorit in cadrul unei tolerante.
Functia care calculeaza raspunsul amplitudinii functiei este oferita in filtmin.m. Aceasta functie foloseste pe
a, coeficientii amplitudinii functiei si pe w, discretizarea domeniului frecventei
de care suntem interesati.
Pentru a forma o problema de atingere a tintei trebuie sa specificam tinta si
precizia pentru aceasta problema. Pentru frecvente intre 0 si 0.l, tinta este
una impusa. Pentru frecvente intre 0.15 si 0.5, tinta este 0. Frecventele intre
0.1 si 0.15 nu sunt specificate, astfel nici o tinta sau precizie nu sunt
necesare in aceasta scara.
Aceasta informatie este inmagazinata in variabila tinta (goal) trecuta in fgoalattain. Lungimea tintei (goal)
este aceeasi cu lungimea returnata de filtmin.
Astfel incat tintele sa fie egal indeplinite, de obicei precizia ar fi introdusa
in abs(goal).
Totusi, intrucat unele tinte
sunt 0, efectul folosirii functiei precizie (weight) weight = abs(goal) va forta
obiectivele cu precizia 0 sa fie indeplinite ca restrictii dificile iar
obiectivul cu precizia 1 sa fie in mod posibil subrealizate (vezi paragraful :
Metoda atingerii tintei al capitolului Introducere in algoritmi).
Fiindca toate tintele sunt apropiate ca amplitudine, folosirea preciziei, a
unitatii pentru toate tintele, le va da prioritate egala ( folosirea abs(goal) pentru precizie este mai
importanta cand amplitudinea tintei difera in mod semnificativ ). De asemenea,
setarea:
options = optimset ( 'GoalsExactAchieve', length (goal) );
specifica faptul
ca fiecare obiectiv ar trebui sa fie cat de aproape posibil de tinta valorii
sale( nici mai mare nici mai mic ).
Pasul 1 : Deschide un M-fisier filtmin.m
function y = filtmin ( a, w )
m = length ( a );
y = cos( w * ( 0:n - l ) * 2 * pi ) * a;
Pasul 2 : Apeleaza programul de optimizare
% inlocuiti cu coeficientii initiali
a0 = ones ( 15, 1 );
incr = 50;
w = linspace( 0, 0.5, incr );
y0 = filtmin ( a0, w );
clf, plot ( w, y0, '-:' );
drawnow;
% rezolva problema alegerii tintei
wl = linspace ( 0, 0.1, incr );
w2 = linspace ( 0.15, 0.5, incr );
w0 = [ wl, w2 ];
goal = [ 1.0 * ones ( l, length
(wl) ) zeros ( l, length (w2) ) ];
weight = ones ( size ( goal ) );
% cheama functia fgoalattain
options = optimset (
'GoalsExactAchieve', length ( goal ) );
[ a, fval, attainfactor, exitflag ]
= fgoalattain ( 'filtmin', a0, goal, weight,
[], [], [], [], [], [], [], options, w0 );
% inlocuiti cu coeficienti optimali
y = filtmin ( a, w );
hold on, plot ( w, y, 'r' )
axis ( [ 0 0.5 - 3 3 ] )
xlabel ( 'Frequency (Hz)' )
ylabel ( 'Magnitude Response (dB)'
)
legend ( 'initial', 'final' )
grid on
Sa comparam amplitudinea frecventei calculata cu coeficientii initiali si
finali (Figura 7.6). Sa notam ca am putea folosi functia firpm in
pachetul de programe al prelucrarii de semnal pentru acesta.