Prob.1 Pentru sistemul de doua grinzi dublu articulate AB si
BC (fig.1.1a), actionat de forta orizontala P aplicata
in B se cere :
a)
Sa se determine valoarea
maxima a fortei P astfel incat sa fie indeplinita
conditia de rezistenta atat in sectiunile barelor AB
si BC cat si in imbinari; pentru imbinarea cu sudura
se va considera ca ls
= 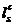 (lungimea de calcul), (fig.1.1b). Datele pentru profilul U8
sunt preluate din STAS 564-80;
(lungimea de calcul), (fig.1.1b). Datele pentru profilul U8
sunt preluate din STAS 564-80;
b)
Sa se determine deplasarea pe
orizontala a punctului B (E
= 2,1×105 N/mm2), neglijand deformatia axiala a
barei BC.
a) Valoarea
maxima a fortei P este
data de valoarea minima a fortei capabile corespunzatoare
capacitatii barelor AB (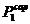 ), BC (
), BC ( ) respectiv a imbinarilor, cu sudura in relief (
) respectiv a imbinarilor, cu sudura in relief ( ) pentru bara AB,
respectiv cu nituri (
) pentru bara AB,
respectiv cu nituri ( ) pentru bara BC.
) pentru bara BC.
Pentru
inceput se vor determina valorile eforturilor in cele doua bare cu
ajutorul ecuatiilor de echilibru al fortelor concurente in nodul B
(fig.1.2):
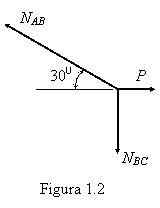 SForizontala = 0
SForizontala = 0  ;
;
SFverticala = 0  .
.
Se vor determina
in continuare valorile maxime ale incarcarilor corespunzatoare
fiecarui element in parte :
bara AB :
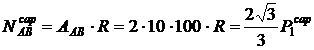
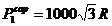 = 1000
= 1000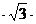 210 ≈ 363370 N = 363,37 kN
210 ≈ 363370 N = 363,37 kN
prinderea cu sudura a barei AB.
Deoarece
este vorba de o sudura de colt se va determina forta
capabila a respectivei suduri, folosindu-se calculul simplificat. De
asemenea se va considera ca lungimea din desen coincide cu lungimea de
calcul a sudurii.
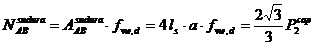
 349181N = 349,181 kN
349181N = 349,181 kN
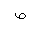
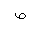
 bara BC :
bara BC : 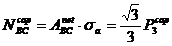 ,
,
unde reprezinta aria neta a sectiunii transversale
si se calculeaza folosind datele corespunzatoare profilului U8
si cele referitoare la nit (vezi fig.1.3) dupa cum urmeaza :
reprezinta aria neta a sectiunii transversale
si se calculeaza folosind datele corespunzatoare profilului U8
si cele referitoare la nit (vezi fig.1.3) dupa cum urmeaza :
 = A - Asl
= 2.AU8
- 2.17.6 = 2.1100 - 204 = 1996 mm2
= A - Asl
= 2.AU8
- 2.17.6 = 2.1100 - 204 = 1996 mm2
 726000N = 726 kN
726000N = 726 kN
prinderea cu nituri a barei BC.
Va
trebui sa se determine in prealabil capacitatea portanta a unui nit.
Deoarece exista doua sectiuni de forfecare s-a multiplicat de
doua ori forta capabila a nitului corespunzatoare unei
sectiuni de forfecare (Fv,Rd).
Referitor la suprafetele strivite se face mentiunea ca 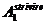 reprezinta
suprafata strivita a platbenzii din nod iar
reprezinta
suprafata strivita a platbenzii din nod iar  reprezinta
suprafata strivita a inimii celor doua profile U8.
reprezinta
suprafata strivita a inimii celor doua profile U8.

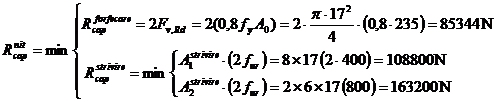 = 85344N
= 85344N
Se va putea scrie: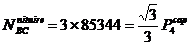
 = 443460N = 443,46
kN.
= 443460N = 443,46
kN.
Capacitatea portanta a sistemului va fi dictata de elementul
cel mai slab.
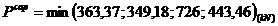
In cazul problemei de fata este vorba de capacitatea
portanta a prinderii prin sudura :
Pcap = 349,18
kN.
Deplasarea pe orizontala a punctului B, in
conditiile date (fig.1.4), are valoarea :

Tinand cont de datele obtinute se gaseste
urmatoarea valoare a deplasarii pe orizontala :

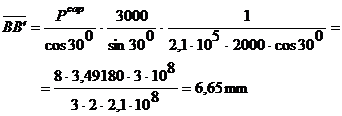
 In baza ipotezei micilor deformatii (fig.1.5) s-a considerat ca
:AB'B = a
In baza ipotezei micilor deformatii (fig.1.5) s-a considerat ca
:AB'B = a
2.
Se considera bara infinit
rigida (nedeformabila) din fig.2a, prinsa articulat in punctele
O si A si actionata de o forta concentrata P
= 120 kN. Se cere dimensionarea
barelor tensionate OD si AC folosind profile cornier cu aripi egale,
precum si calculul deplasarii pe verticala a punctului B.
Sa se analizeze de asemenea situatia in care dispare pendulul din
punctul O si este inlocuit de o articulatie (fig.2b). Se considera ca barele sunt
alcatuite din otel S235 cu R = 210MPa = 21kN/cm2 si E = 210GPa = 2,1×105N/mm2.
SM)O = 0 -
1,5 NAC + 2,5P = 0 NAC = 200 kN
SM)A = 0 -
1,5 NOD + P = 0 NOD = 80 kN
Verificare: (SF)Verticala = 0 NAC - NOD - P = 0.
Dimensionarea
barelor:
pentru bara AC:
 cm2
cm2 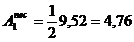 cm2.
cm2.
Cornierul
L50×50×5 are aria efectiva 4,80 cm2. Deci sectiunea
efectiva a barei AC (sectiunea 2-2 din fig.2a) va avea aria 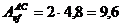 cm2.
cm2.
Verificarea
sectiunii alese:
 kN/cm2 = 208,3 MPa < R = 210 MPa
kN/cm2 = 208,3 MPa < R = 210 MPa
pentru bara OD:
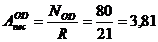 cm2
cm2 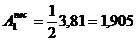 cm2.
cm2.
Cornierul
L35×35×3 are aria efectiva 2,04 cm2. Deci sectiunea
efectiva a barei AC (sectiunea 1-1 din fig.2a) va avea aria 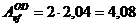 cm2.
cm2.
Verificarea
sectiunii alese:
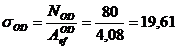 kN/cm2 = 196,1 MPa
kN/cm2 = 196,1 MPa
Calculul
alungirilor barelor si a deplasarii pe verticala a punctului
B(fig.2a):
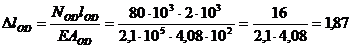 mm
mm
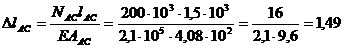 mm
mm
Pentru
evaluarea deplasarii pe verticala a punctului B DB din fig.2a) se vor srie rapoartele din triunghiurile asemenea si folosind
proprietatile rapoartelor se va ajunge la:
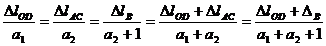
Utilizarea
ultimelor doua rapoarte va conduce la:
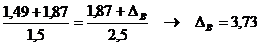 mm.
mm.
In
ceea ce priveste sistemul din fig.2b se observa ca dispare bara
OD, dar efortul din bara AC va fi acelasi cu cel din structura din fig.2a.
Se va modifica valoarea deplasarii pe verticala a punctului B.
Utilizarea relatiilor de asemanare (fig.2b) va conduce la:
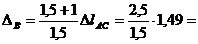 2,48 mm.
2,48 mm.
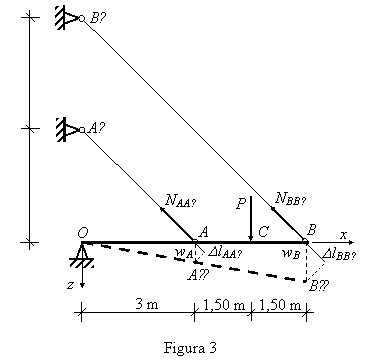
3 . Se cere calcularea eforturilor
din tirantii ce sustin grinda
infinit rigida din fig.3 actionata de forta P = 360 kN. Sa se dimensioneze tirantii din
profile cornier cu aripi egale, stiind ca amandoi tirantii au
aceeasi arie A si sa se calculeze deplasarea pe verticala a
punctului B (wB). Se
considera ca barele sunt alcatuite din otel S235 cu:
R
= 210MPa = 21kN/cm2 si
E = 210GPa = 2,1×105N/mm2.
Pentru inceput se
fac urmatoarele observatii:
unghiurile facute de tiranti cu bara orizontala sunt egale intre
ele si au valoarea de 45 , iar lungimea barei BB′
este dubla fata de cea a barei AA′ (conform datelor
numerice).
Sistemul fiind
static nedeterminat, la ecuatiile de echilibru (una in cazul de
fata) se va adauga cea de compatibilitate a defor-
matiilor. Urmarind
fig.3 se poate constata usor ca :
wB = 2wA DlBB′ = 2DlAA′.
Sistemul de ecuatii va fi
de forma:
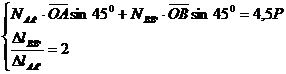
Explicitarea
celei de-a doua relatii a sistemului conduce la:

Relatia
de mai sus se va introduce in prima ecuatie a sistemului, rezultand:
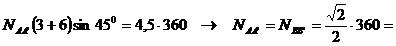 254,56 kN.
254,56 kN.
O
alta remarca interesanta este aceea ca pentru sistemul
dat, valoarea reactiunii verticale
din punctul O este zero (lucru usor de verificat cu ajutorul ecuatiei
de echilibru de proiectie pe verticala a fortelor).
Pentru
dimensionare se va utiliza relatia:
 cm2.
cm2.
Sectiunea
transversala va fi alcatuita din doua profile cornier cu
aripi egale :
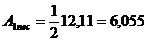 cm2.
cm2.
Cautarea
in tabele conduce la profilul cornier L50×50×7 cu aria efectiva A = 6,56
cm2.
Pentru
calculul deplasarii pe verticala a punctului B se poate observa
(fig.3) ca:
 11,1 mm = 1,11 cm.
11,1 mm = 1,11 cm.
.
Fie o bara cilindrica de cupru introdusa intr-un tub de
otel (fig.4). Sa se determine alungirile celor doua elemente
atunci cand se produce o crestere DT = 500C considerand in faza initiala ca cele
doua bare sunt prinse doar la un capat si apoi ca ele sunt
solidarizate si la celalalt cap.
Date numerice: diametrul barei de cupru dcu = 50 mm, di
= 54mm (di reprezinta
diametrul interior al tubului de otel), t = 5mm (grosimea tubului de otel), l = 2m, Ecu =
120 GPa = 1,2×104kN/cm2, Eol = 2,1×104kN/cm2, acu = 17×10 - 6 (0C)
-1 , aol = 12×10 - 6 (0C) -1.
In
situatia in care barele sunt fixate doar la un singur capat,
dilatarea celor doua bare este libera, astfel ca nu apar eforturi
in structuri. Se vor produce preponderent
alungiri ale barelor pe directia longitudinala. Valorile lor
vor fi:
pentru bara din cupru:
Dlcu acuDTl = 17×10-6×50×2000 = 1,7 mm
pentru bara de otel:
Dlol aolDTl = 12×10-6×50×2000 = 1,2 mm
In urma fixarii lor
si la celalalt capat, ele sunt obligate sa aiba
aceeasi alungire finala, cuprinsa intre cele doua valori
initiale, 1,7, respectiv 1,2mm. In consecinta bara de otel
se va alungi peste 1,2mm cu cantitatea Dl′ care va introduce un efort de intindere in respectiva
bara:
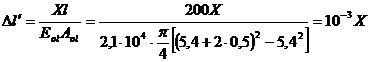 ,
,
in timp ce in bara
de cupru se va dezvolta un efort de compresiune care va avea drept efect
reducerea dilatarii totale cu cantitatea (1,7 - 1,2 - Dl′). Valoarea sa va fi tot X, din ratiuni de echilibru. Se va
putea scrie:
 .
.
Coroborand cele doua
relatii se ajunge la:
 = 52,63 kN
= 52,63 kN
5.
Bara tronconica din fig.5 este incastrata la capete iar raportul
diametrelor celor doua baze este b/a
= 2. Stiind ca se produce o scadere a temperaturii de montaj cu DT = 500C se cere determinarea
efortului ce se dezvolta in bara precum si valoarea tensiunii
maxime. Se cunosc:
a = 20 cm ;
E =
210 GPa = 2,1×104 kN/cm2 ; R =
210 MPa
at = 12×10 -6 0C
-1 (coeficientul de dilatare termica al materialului).
 Ca urmare a contractiei
impiedicate a barei se va dezvolta un efort de intindere al carui efect va
fi acela de a contrabalansa scurtarea barei :
Ca urmare a contractiei
impiedicate a barei se va dezvolta un efort de intindere al carui efect va
fi acela de a contrabalansa scurtarea barei :
Dl = latDT = 
Diametrul barei la cota
x va avea valoarea :  , astfel ca aria sectiunii transversale la cota
mentionata va fi:
, astfel ca aria sectiunii transversale la cota
mentionata va fi:

Deci
se va putea scrie:
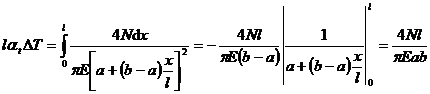
cu solutia:
 =
= 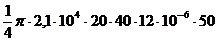 = 7917 kN.
= 7917 kN.
Tensiunea maxima se produce in
sectiunea de diametru a:
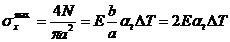 =
=  25,2 kN/cm2 = 252 MPa > R.
25,2 kN/cm2 = 252 MPa > R.
Observatii:
efortul din bara (N) nu depinde de lungimea barei;
totusi daca bara este prea lunga se pune problema pierderii
stabilitatii ei (pierderea formei de echilibru stabil) ;
tensiunea din bara la randul
ei nu depinde de lungimea barei, dar nici de valoarea diametrelor de la capete
ci de raportul lor;
in cazul concret al barei din
problema se observa ca se depaseste
rezistenta materialului atata timp cat se mentine raportul 2 dintre
diametre;
daca bara este cu
sectiune constanta se va observa ca tensiunea scade de doua
ori, indiferent de valoarea diametrului.
 6. Se da grinda cu zabrele din fig.6.1a. Se cere
dimensionarea barei 46 si a prinderii sale la nod, stiind ca
prinderea barei la nod se face prin sudura/nituri (R = 210 N/mm2
= 21 kN/cm2). Sectiunea transversala va fi
alcatuita din corniere cu aripi egale (fig.6.1b - tc = grosimea aripii cornierului,
tg = grosimea
guseului ; se va considera ca tg
= 1,5tc).
6. Se da grinda cu zabrele din fig.6.1a. Se cere
dimensionarea barei 46 si a prinderii sale la nod, stiind ca
prinderea barei la nod se face prin sudura/nituri (R = 210 N/mm2
= 21 kN/cm2). Sectiunea transversala va fi
alcatuita din corniere cu aripi egale (fig.6.1b - tc = grosimea aripii cornierului,
tg = grosimea
guseului ; se va considera ca tg
= 1,5tc).
Se vor determina pentru inceput
valorile reactiunilor :
 kN
kN
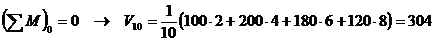 kN
kN
Verificarea
corectitudinii calculelor se face cu ajutorul ecuatiei de echilibru de
forte pe verticala, observandu-se ca se obtine valoarea
zero.
Pentru calculul efortului din bara
46 se va aplica metoda sectiunilor (linia punctata din fig.6.1a)
si se va scrie ecuatia de echilibru de moment in raport cu punctul 5
al oricarei parti din structura, in cazul de fata
pentru partea de grinda cu zabrele din stanga sectionarii
practicate :
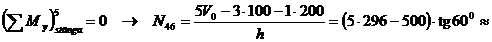 1697,4 kN.
1697,4 kN.
Dimensionarea barei, considerand
ca solidarizarea se face prin sudura :
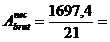 80,83 cm2.
80,83 cm2.
Sectiunea fiind
alcatuita din doua corniere, va rezulta ca va trebui
cautat un cornier a carui arie sa fie mai mare de:
 40,415 cm2.
40,415 cm2.
Cornierul ce satisface acest
deziderat este L140×140×16 a carui arie este de 42,2 cm2.
Pentru profilul cornier mentionat se se vor mai scoate urmatoarele
date (fig.6.2a):
a = 14 cm; e = 4,20 cm; tg = 1,5×1,6 = 2,4 cm.
Se
observa ca este indeplinita relatia de verificare:
 kN
kN
Se va proceda in continuare la
dimensionarea cordoanelor de sudura in relief. Ca necunoscute vor fi
grosimile cordoanelor de sudura, respectiv lungimile lor (fig.6.2a,b).
Pentru inceput se vor calcula
valorile eforturilor ce vor fi transmise la nod prin intermediul cordoanelor de
sudura. Se va utiliza ecuatia de echilibru de moment pentru
determinarea valorilor:
pentru efortul ce revine
cordoanelor de la baza cornierelor (N1
- fig.6.2a) se va scrie o ecuatie de moment in raport cu un punct situat
pe suportul fortei N2:
aN - (a - e)Nt,Rd = 0 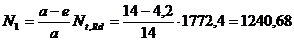 kN
kN
pentru efortul ce revine
cordoanelor de la partea superioara a cornierelor (N2 - fig.6.2a) se va scrie o ecuatie de moment in
raport cu un punct situat pe suportul fortei N1:
aN - eNt,Rd = 0  kN
kN
Se observa ca utilizarea
acelorasi grosimi de sudura pentru cordoanele superioare si cele
inferioare ar duce la diferente mari de lungime intre ele. De aceea se
prefera utilizarea unor grosimi diferite. Ideal ar fi ca toate cele patru
cordoane de sudura sa aiba aceeasi lungime. Se va
cauta raportul dintre grosimile de sudura as1/as2 pentru care ar fi indeplinita
aceasta conditie. Se poate scrie:
 2,33
2,33
unde  , respectiv
, respectiv  reprezinta valoarea
fortei de forfecare pe unitatea de lungime corespunzatoare
cordoanelor de sudura de la partea inferioara, respectiv
superioara.
reprezinta valoarea
fortei de forfecare pe unitatea de lungime corespunzatoare
cordoanelor de sudura de la partea inferioara, respectiv
superioara.
Daca se considera, spre
exemplu, pentru as2
= 3mm, grosimea minima admisa pentru un cordon de sudura, va
rezulta ca va trebui ca as1
= 3 × 2,33 = 7mm. Dimensiunea maxima a grosimii sudurii de la partea
inferioara este (vezi fig.3.29d):
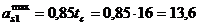 mm,
mm,
astfel ca se
pot folosi grosimile cordoanelor de sudura propuse.
Se atrage atentia ca
totusi analiza este mai complicata si ca aceasta
abordare este simplista.
Conform dimensiunilor grosimilor
cordoanelor de sudura se va obtine lungimea lor, utilizand oricare
egalitate din setul de mai sus:
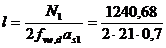 = 42,2 cm.
= 42,2 cm.
Se va observa ca lungimea
cordonului de sudura depaseste lungimea maxima a unui
cordon de sudura admisa se standard: 60as = 60×7 = 420 mm. In acelasi timp lungimea
cordoanelor de sudura este relativ mare, raportata la distanta
dintre doua noduri consecutive, astfel ca s-ar impune utilizarea unor
grosimi de sudura mai mari. Masurile constructive vor fi aprofundate
la cursul de metal.
Lungimea efectiva a cordonului
de sudura se obtine prin:
ls =
l + 2as1 = 42,2 + 2×0,7 = 43,6 cm.
Dimensionarea barei considerand
ca prinderea barei la capete se face cu nituri :
 ≈ 93 cm2,
≈ 93 cm2,
astfel ca aria unui
cornier va trebui sa fie in jurul
valorii: 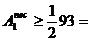 46,5 cm2.
46,5 cm2.
Conform tabelului corespunzator
cornierelor cu aripi egale se pot folosi L150×150×16, avand aria sectiunii
transversale egala cu 45,7 cm2, fie L160×160×16 cu aria
egala cu 49,1 cm2
Se va proceda la verificarea
primului cornier (L150×150×16). Datele de calcul vor fi:
a = 15 cm; e = 4,29 cm; tg = 1,5×1,6 = 2,4 cm.
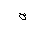
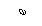
 Se propune utilizarea
unor nituri cu diametrul de 20 mm, pentru care diametrul de calcul este de d = 21mm. Calculul ariei nete a
sectiunii transversale (fig.6.3b) va conduce la:
Se propune utilizarea
unor nituri cu diametrul de 20 mm, pentru care diametrul de calcul este de d = 21mm. Calculul ariei nete a
sectiunii transversale (fig.6.3b) va conduce la:
Anet = Abruta - Aslabiri = 2 (45,7 -
1,6×2,1) = 84,68 cm2.
Verificarea sectiunii propuse:
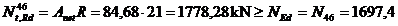 kN
kN
Se observa ca desi
aria bruta efectiva a iesit mai mica decat cea
necesara, totusi bara s-a verificat. Explicatia este simpla
si consta in faptul ca slabirea reala produsa de
nit este mai mica de 15%, cat s-a presupus initial.
Dimensionarea prinderii va consta in
determinarea numarului de nituri necesar preluarii efortului
efortului rezistent al barei ( ). Se va determina efortul capabil al unui nit:
). Se va determina efortul capabil al unui nit:
 = 130,3 kN.
= 130,3 kN.
Numarul
necesar de nituri va rezulta ca fiind:
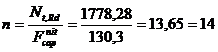 .
.
Problema care apare este legata
de lungimea totala a guseului pe zona 4-6 pentru a introduce toate cele 14
nituri. Conform fig.3.22a si Anexa 1.3, ar rezulta in cazul concret o
lungime minima necesara:
lnec
= 2e1 + 13p1 = 2×(1,2d0) + 13×(2,2d0) = 65,1cm
ceea ce in cazul concret al distantei
de 2m dintre doua noduri consecutive se dovedeste a fi mare.
Se poate folosi, spre exemplu, un
nit cu diametrul mai mare, dar s-ar putea ca sectiunea transversala propusa
sa nu se mai verifice, impunandu-se o sectiune mai puternica.
Sau s-ar putea apela la dispunerea niturilor pe doua randuri (fie o
dispunere in randuri paralele, fie o dispunere decalata a lor pe cele
doua randuri), fara modificarea deci a diametrului propus. Dar
si in acest caz ar trebui reluata verificarea barei. Ca si in
cazul dimensionarii cordoanelor de sudura, nu se continua
analiza privind lungimea necesara efectiva.
Pentru sistemul din fig.7.1a
se cere determinarea eforturilor din elementele intinse (bara orizontala
se considera infinit rigida), dimensionarea prinderilor considerand
ca sunt realizate prin sudura, respectiv nituire si calculul
deplasarii pe verticala (w2)
a punctului de aplicatie a fortei concentrate P = 1200 kN. Se vor analiza trei cazuri:
a) Ariile
tirantilor sunt egale intre ele: A1
= A3 = A0 ;
b) A1 = A0 ; A3
= 1,5A0 ;
c) A1 = 1,5A0 ; A3
= A0 ;
Sectiunile
transversale ale tirantilor vor fi realizate cu ajutorul a doua
corniere cu aripi egale (fig.7.1b), grosimea guseului (tg) de prindere fiind cu 50% mai mare decat cea a
cornierelor (tc). Date
suplimentare: R = 210MPa = 21 kN/cm2;
E = 210 GPa = 2,1×104
kN/cm2.
Sistemul
este o data static nedeterminat. Relatiile ce vor permite
determinarea eforturilor din tiranti sunt:
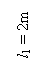


a) Cazul : A1 = A3
= A0 . Se observa
ca N1 = N2 = 0,5P = 600 kN
Dimensionarea
barei, considerand ca solidarizarea se face prin sudura :

 28,58 cm2
28,58 cm2 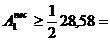 14,29 cm2.
14,29 cm2.
Cornierul ce satisface acest
deziderat este L90×90×9 (fig.7.2b) a carui arie este de 15,5 cm2.
Pentru profilul cornier mentionat se vor mai scoate urmatoarele date:
a = 9 cm; e = 2,54 cm; tg = 1,5×0,9 ≈ 1,4 cm.
Se
observa ca este indeplinita relatia de verificare:
 kN
kN
La determinarea lungimii cordonului
de sudura se va folosi procedeul de la problema anterioara, astfel
ca se vor mai relua doar calculele, fara alte justificari,
cu mentiunea valabila in continuare ca abordarea este
simplista.
a - (a - e)Nt,Rd =
0
- (a - e)Nt,Rd =
0 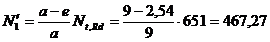 kN
kN
a - eNt,Rd = 0
- eNt,Rd = 0  kN
kN
 2,54
2,54
Determinarea
grosimilor cordoanelor de sudura:
3 ≤ as1
≤ 0,85×9 = 7,65 mm
3 ≤ as2
≤ 0,7×9 = 6,3 mm
Pentru cordonul de sudura l1 se va considera ca
grosimea sa este as1
= 7mm, iar pentru celalalt cordon as2
= 4 mm. Lungimile cordoanelor vor fi (fig.7.2a):
 = 15,9 cm
= 15,9 cm
 = 10,94 cm.
= 10,94 cm.
Lungimile efective se vor obtine adaugand
pentru fiecare cordon cate o grosime de sudura:
ls1
= l1 + as1 = 15,9 + 0,7 =
16,6 cm;
ls2
= l2 + as2 = 10,94 + 0,4
= 11,34 cm = 11,4 cm.
Calculul alungirilor in situatia prinderii barelor
prin sudura :
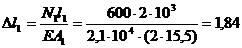 mm; Dl Dl = 2×1,84 =
3,68 mm.
mm; Dl Dl = 2×1,84 =
3,68 mm.
Deplasarea pe verticala a punctului 2 va fi:
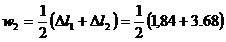 = 2,76
= 2,76
Dimensionarea
tirantilor considerand ca prinderea se face cu nituri:
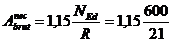 ≈ 32,86 cm2
≈ 32,86 cm2 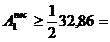 16,43 cm2.
16,43 cm2.
Din tabelul de profile cornier se
gaseste ca L90×90×10 satisface conditia. Date de calcul:
Abrut = 17,10 cm2; a = 9 cm; e
= 2,58; tg = 1,5tc
= 1,5×1 = 1,5cm
Se propune utilizarea niturilor de
diametru 20mm, pentru care diametrul de calcul este de 21mm. Calculele se vor
derula dupa cum urmeaza:
Anet = Abruta - Aslabiri = 2 (17,1 -
1×2,1) = 30 cm2.
Verificarea sectiunii propuse:
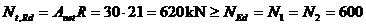 kN
kN
 = 130,3 kN.
= 130,3 kN.
Numarul
necesar de nituri va rezulta ca fiind:
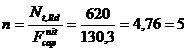 nituri.
nituri.
Calculul alungirilor in situatia prinderii barelor
cu nituri (se va lucra cu aria bruta a sectiunii transversale) :
 mm; Dl Dl = 2×1,67 =
3,34 mm.
mm; Dl Dl = 2×1,67 =
3,34 mm.
Deplasarea pe verticala
a punctului 2 va fi:
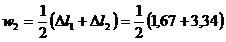 = 2,51 mm
= 2,51 mm
b) A = A0 ; A3 = 1,5A0.
Eforturile ce se dezvolta in tiranti au valorile:

Dimensionarea
tirantilor, considerand ca solidarizarea se face prin sudura
(3.27) :
dimensionarea tirantului 1:
 21,43 cm2 L60×60×10 cu aria: A1 = 11,1 cm2
21,43 cm2 L60×60×10 cu aria: A1 = 11,1 cm2
a = 6 cm; e = 1,85cm; tg = 1,5×1 = 1,5 cm
Verificarea: 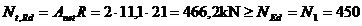 kN .
kN .
Dimensionarea prinderii prin
sudura. In cele ce urmeaza, inclusiv la punctul c al problemei, se
considera ca notatiile eforturile preluate de cordoanele de
sudura sunt cele din fig.7.2a,b.
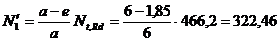 kN
kN
 kN
kN
Determinarea grosimilor cordoanelor
de sudura considerand ca as1
= 7mm si as2
= 4mm
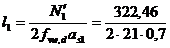 = 10,97 cm
= 10,97 cm
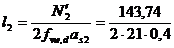 = 8,56 cm.
= 8,56 cm.
dimensionarea tirantului 3:
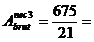 32,14 cm2 L90×90×10 cu aria: A2
= 17,1 cm2
32,14 cm2 L90×90×10 cu aria: A2
= 17,1 cm2
a = 9 cm; e = 2,58cm; tg = 1,5×1 = 1,5 cm
Verificarea: 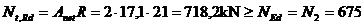 kN
kN
Dimensionarea sudurii
 kN
kN
 kN
kN
Determinarea grosimilor cordoanelor
de sudura considerand ca as1
= 8mm si as2
= 4mm
 = 15,25 cm
= 15,25 cm
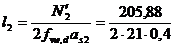 = 12,25 cm.
= 12,25 cm.
Se
mai face o verificare suplimentara. Se reaminteste faptul ca
eforturile in bare s-au obtinut considerandu-se ca intre ariile lor
exista relatia 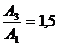 astfel ca se
impune verificarea existentei relatiei mentionate in cazul
ariilor efective:
astfel ca se
impune verificarea existentei relatiei mentionate in cazul
ariilor efective: 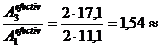 1,50.
1,50.
Se va urmari ce implicatii are faptul ca
totusi raportul real este 1,54:
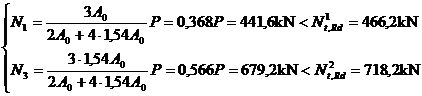
Practic se observa, in acest caz
o usoara modificare a valorilor eforturilor efective.
Calculul alungirilor in situatia prinderii barelor
prin sudura :
 mm; Dl Dl = 2×1,93 =
3,86 mm.
mm; Dl Dl = 2×1,93 =
3,86 mm.
Deplasarea pe verticala a punctului 2 va fi:
 = 2,89mm
= 2,89mm
Dimensionarea
tirantilor considerand ca prinderea se face cu nituri:
-
dimensionarea tirantului1
 ≈ 24,64 cm2
≈ 24,64 cm2 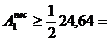 12,32 cm2.
12,32 cm2.
Din tabelul de profile cornier se
gaseste ca L80×80×8 satisface conditia. Date de calcul:
Abrut = 12,30 cm2; a = 8 cm; e
= 2,26 tg = 1,5tc
= 1,5×0,8 = 1,2cm
Se propune utilizarea niturilor de
diametru 16mm, pentru care diametrul de calcul este de 17mm. Calculele se vor
derula dupa cum urmeaza:
Anet = Abruta - Aslabiri = 2 (12,3 -
0,8×1,7) = 21,88 cm2.
Verificarea sectiunii propuse:
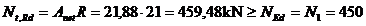 kN
kN
-
dimensionarea tirantului 3
 ≈ 36,96 cm2
≈ 36,96 cm2 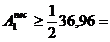 18,48 cm2.
18,48 cm2.
Din tabelul de profile cornier se
gaseste ca L90×90×11 satisface conditia. Date de calcul:
Abrut = 18,70 cm2; a = 9 cm; e
= 2,62 tg = 1,5tc
= 1,5×1,1 = 1,65cm
Se propune utilizarea niturilor de
diametru 16mm, pentru care diametrul de calcul este de 17mm. Calculele se vor
derula dupa cum urmeaza:
Anet = Abruta - Aslabiri = 2 (18,70 -
1,1×1,7) = 33,66 cm2.
Verificarea sectiunii propuse:
 kN
kN
Se mai face verificarea raportului
dintre ariile celor doi tiranti:
 = 1,52 ≈ 1,50
= 1,52 ≈ 1,50
Determinarea numarului de
nituri pentru primul tirant:
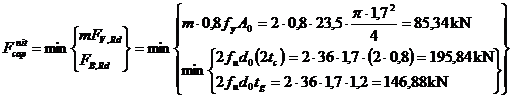 = 85,34 kN.
= 85,34 kN.
Numarul
necesar de nituri va rezulta ca fiind:
 nituri.
nituri.
Determinarea numarului de
nituri pentru al doilea tirant:
 = 85,34 kN.
= 85,34 kN.
Numarul
necesar de nituri va rezulta ca fiind:
 nituri.
nituri.
Calculul alungirilor in situatia prinderii barelor cu
nituri (se va lucra cu aria bruta a sectiunii transversale) :
 mm; Dl Dl = 2×1,74 =
3,48 mm.
mm; Dl Dl = 2×1,74 =
3,48 mm.
Deplasarea pe
verticala a punctului 2 va fi:
 = 2,61 mm.
= 2,61 mm.
c) A = 1,5A0 ; A3 = A0.
Eforturile ce se dezvolta in tiranti au valorile:
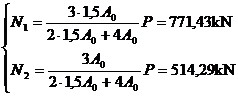
Dimensionarea
tirantilor, considerand ca solidarizarea se face prin sudura :
dimensionarea tirantului 1:
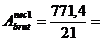 36,73 cm2 L90×90×11 cu aria: A1 = 18,7 cm2
36,73 cm2 L90×90×11 cu aria: A1 = 18,7 cm2
a = 9 cm; e = 2,62 tg
= 1,5tc = 1,5×1,1 = 1,65cm
Verificarea: 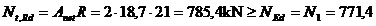 kN
kN
Dimensionarea sudurii
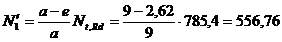 kN
kN
 kN
kN
Determinarea grosimilor cordoanelor
de sudura considerand ca as1
= 8mm si as2
= 4mm
 = 16,57 cm
= 16,57 cm
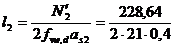 = 13,61 cm.
= 13,61 cm.
dimensionarea tirantului 3:
 24,49 cm2 L90×90×10 cu aria: A2
= 12,3 cm2
24,49 cm2 L90×90×10 cu aria: A2
= 12,3 cm2
a = 9 cm; e = 2,58 tg
= 1,5tc = 1,5×1,0 = 1,5cm
Verificarea:  kN
kN
Dimensionarea sudurii
 kN
kN
 kN
kN
Determinarea grosimilor cordoanelor
de sudura considerand ca as1
= 8mm si as2
= 4mm
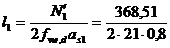 = 10,97 cm
= 10,97 cm
 = 8,81 cm.
= 8,81 cm.
Se
reia verificarea suplimentara privind conditia ca 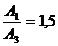 . Se observa ca:
. Se observa ca:
 1,50.
1,50.
Calculul alungirilor in situatia prinderii barelor
prin sudura :
 mm; Dl Dl = 2×1,96 =
3,92 mm.
mm; Dl Dl = 2×1,96 =
3,92 mm.
Deplasarea pe verticala a punctului 2 va fi:
 = 2,94mm
= 2,94mm
Dimensionarea
tirantilor considerand ca prinderea se face cu nituri:
-
dimensionarea tirantului1
 ≈ 42,24 cm2
≈ 42,24 cm2 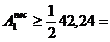 21,12 cm2.
21,12 cm2.
Din tabelul de profile cornier se
gaseste ca L100×100×12 satisface conditia. Date de calcul:
Abrut = 22,70 cm2; a = 10 cm; e
= 2,9 tg
= 1,5tc = 1,5×1,2 = 1,8cm
Se propune utilizarea niturilor de
diametru 20mm, pentru care diametrul de calcul este de 21mm. Calculele se vor
derula dupa cum urmeaza:
Anet = Abruta - Aslabiri = 2 (22,7 -
1,2×2,1) = 40,36 cm2.
Verificarea sectiunii propuse:
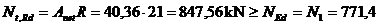 kN
kN
-
dimensionarea tirantului 2
 ≈ 28,16 cm2
≈ 28,16 cm2  14,08 cm2.
14,08 cm2.
Din tabelul de profile cornier se
gaseste ca L90×90×9 satisface conditia. Date de calcul:
Abrut = 15,50 cm2; a = 9 cm; e
= 2,50 tg = 1,5tc
= 1,5×0,9 = 1,35cm
Se propune utilizarea niturilor de
diametru 16mm, pentru care diametrul de calcul este de 17mm. Calculele se vor
derula dupa cum urmeaza:
Anet = Abruta - Aslabiri = 2 (15,50 -
0,9×2,1) = 27,62 cm2.
Verificarea sectiunii propuse:
 kN
kN
Se mai face verificarea raportului
dintre ariile celor doi tiranti:
 = 1,46 ≈ 1,50
= 1,46 ≈ 1,50
Determinarea numarului de
nituri pentru primul tirant:
 = 130,3 kN.
= 130,3 kN.
Numarul
necesar de nituri va rezulta ca fiind:
 nituri.
nituri.
Determinarea numarului de
nituri pentru al doilea tirant:
 = 130,3kN.
= 130,3kN.
Numarul
necesar de nituri va rezulta ca fiind:
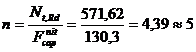 nituri.
nituri.
Calculul alungirilor in situatia prinderii barelor
cu nituri (se va lucra cu aria bruta a sectiunii transversale) :
 mm; Dl Dl = 2×1,62 =
3,24 mm.
mm; Dl Dl = 2×1,62 =
3,24 mm.
Deplasarea pe
verticala a punctului 2 va fi:
 = 2,43 mm.
= 2,43 mm.
Se
va face o analiza a celor trei cazuri prezentate prin prisma
modificarii unui parametru si anume a relatiei dintre ariile
tirantilor. Datele sunt centralizate in Tabel 7.1.
Tabel
7.1
|
Caz:
|
Imbinare
cu sudura
|
Imbinare
cu nituri
|
|
w
|
A (cm2)
|
A
|
A + A3
|
w
|
A (cm2)
|
A
|
A + A3
|
|
A = A3
|
|
|
|
|
|
|
|
|
|
A =1,5A1
|
|
|
|
|
|
|
|
|
|
A =1,5A3
|
|
|
|
|
|
|
|
|
O
scurta privire asupra datelor centralizatoare indica
urmatoarele:
utilizarea sudurii in locul
prinderii cu nituri aduce economie de material;
cazul b de distributie a
ariilor (A3 = 1,5A1) este cel mai avantajos
din punctul de vedere al economiei de material;
in cazul imbinarii cu suduri,
cazul in care ariile celor doi tiranti sunt egale conduce la sistemul cel
mai rigid, in timp ce in cazul prinderii cu nituri cel mai rigid s-a dovedit a
fi cazul c. Se poate afirma, pentru problema data, ca modificarea
rigidatilor axiale nu produce modificari puternice ale
deformatiilor.





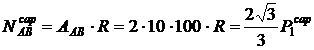


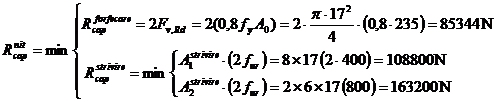 = 85344N
= 85344N
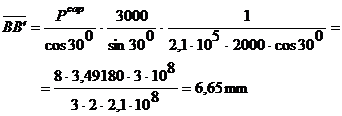

 kN/cm2 = 208,3 MPa < R = 210 MPa
kN/cm2 = 208,3 MPa < R = 210 MPa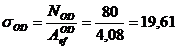 kN/cm2 = 196,1 MPa
kN/cm2 = 196,1 MPa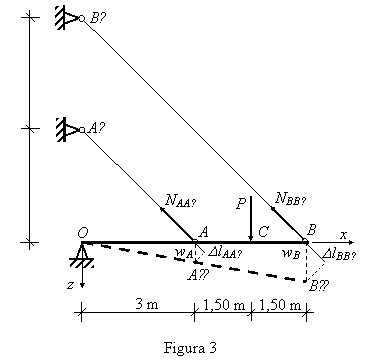
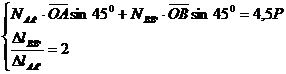



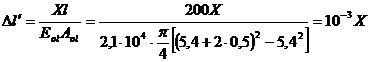 ,
, .
.


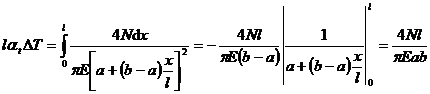


 2,33
2,33
 = 130,3 kN.
= 130,3 kN.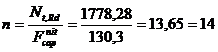 .
.


 = 130,3 kN.
= 130,3 kN.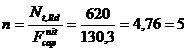 nituri.
nituri.
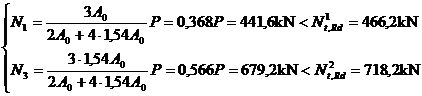
 = 1,52 ≈ 1,50
= 1,52 ≈ 1,50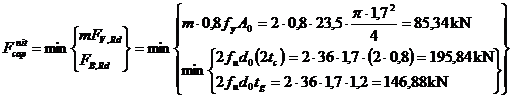 = 85,34 kN.
= 85,34 kN. nituri.
nituri. = 85,34 kN.
= 85,34 kN. nituri.
nituri.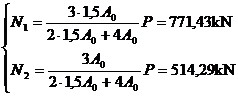
 = 130,3 kN.
= 130,3 kN. nituri.
nituri. = 130,3kN.
= 130,3kN.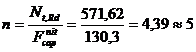 nituri.
nituri.