GESTIUNEA STOCURILOR
Discontinuitatile in livrare determina managerii
intreprinderilor sa stocheze marfuri, pentru a absorbi cererile
aleatoare. Deoarece stocarea unui produs are un cost (datorat imobilizarii
de fonduri, pazei, degradarii, etc.), tendinta este de a stoca o
cantitate cat mai mica. Pe de alta parte o politica de a avea
stocuri cat mai mici, implica reaprovizionari mai dese, care pot
sa induca: costuri de reaprovizionare si pierderi de profit in
cazul rupturilor de stoc (clientii neputand sa astepte, se
adreseaza concurentei). In fata unei cereri fluctuante, trebuie
sa fie definita o regula de reaprovizionare, (momentul
efectuarii comenzii si cantitatea comandata), care sa
conduca la o suma minima a cestor costuri.
MODELUL WILSON
Modelul Wilson
este un model determinist care realizeaza calculul principalilor
parametrii de gestiune in conditiile optimizarii costurilor totale de
stocare pentru un articol.
Ipotezele modelului si
notatii:
BA -
cererea anuala care se presupune
ca este repartizata uniform in timp, adica viteza de iesire
din stoc este constanta.
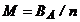 - cererea pe unitatea de timp (astfel n = 1, 12, 52, dupa cum unitatea
de timp este anul, luna, saptamana,).
- cererea pe unitatea de timp (astfel n = 1, 12, 52, dupa cum unitatea
de timp este anul, luna, saptamana,).
Q - comanda (cantitatea de aprovizionare).
SS -
stocul de securitate; comanda
soseste inainte ca stocul sa se epuizeze - stocul de securitate
permite satisfacerea unor cereri neprevazute. In aceasta etapa a
prezentarii modelului, stocul de securitate apare ca o cantitate fixa,
data. Acesta nu are nici un rol in calculul nostru de optimizare.
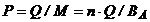 - durata unui ciclu de aprovizionare.
- durata unui ciclu de aprovizionare.
CA -
costul de aprovizionare (lansare a
comenzii).
Comentariu. Acest cost este diferit daca
articolul este cumparat sau realizat in intreprindere.
- Daca articolul este cumparat acest
cost cuprinde: costurile de achizitie (alegerea furnizorului, negocierea,
controlul facturilor,) si de receptie (intrarea si
inregistrarea articolului in stoc). Aceste costuri includ cheltuieli de
personal, consumabile, cheltuieli postale si si de comunicatie,
precum si amortizarile corespunzatoare. Se poate determina
impartind bugetul serviciului aprovizionare la numarul total de
comenzi prelucrate.
- Daca articolul este produs de intreprindere
acest cost cuprinde: costurile de lansare in fabricatie (reglajul
masinilor, pregatirea materialelor si componentelor, rebuturi de
lansare) si costurile de receptie a articolelor fabricate.
CS -
costul de stocare.
Comentariu. Acest cost cuprinde costul de oportunitate
al capitalului imobilizat in stoc, costurile de depozitare (amortizare,
paza, incalzire/racire, gestiune,), costurile de deteriorare,
depasire valabilitate, furt si asigurari. Acest cost se
considera in general o fractie din costul articolului, de exemplu
aproximativ 0.2.
pu -
pretul unitar al articolului.
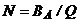 - numarul
anual de aprovizionari.
- numarul
anual de aprovizionari.
Se obtine astfel evolutia stocului redata in Figura 1:
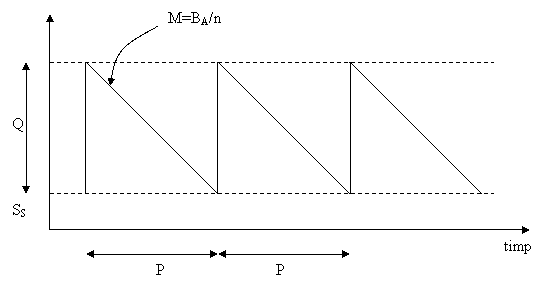
Figura 1
Rezolvare:
Se determina:
- valoarea medie anuala a stocului 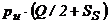
- costul anual de stocare C1 = 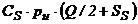
costul anual de aprovizionare C2 = 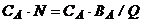
Rezulta costul total anual de stocare:
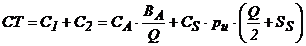 (1)
(1)
- calculam
min CT(Q)
din 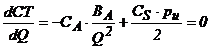 =>
=>
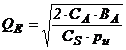 (2)
(2)
unde: QE reprezinta
cantitatea economica ("lotul economic") , marimea optima a
comenzii de aprovizionare,
care minimizeaza costul total anual de stocare.
Se deduce:
- ciclul optim de
aprovizionare (perioada economica): 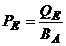 (in ani)
(in ani)
- numarul
optim anual de comenzi (frecventa
economica): 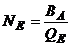
Comentariu. Cele doua costuri de aprovizionare
si stocare, CA si
CB , influenteaza
diferit marimea cantitatii
economice QE , data de relatia (2). Astfel, o crestere a costului de
aprovizionare va conduce la cresterea cantitatii economice
si implicit la micsorarea numarului de comenzi, in timp ce
cresterea costului de stocare diminueaza volumul comenzii si implicit nivelul mediu al
stocului. Evolutiile celor doua costuri anuale (C1 si C2
) si a costului total (CT),
in functie de marimea comenzii (Q)
sunt redate in Figura 2.
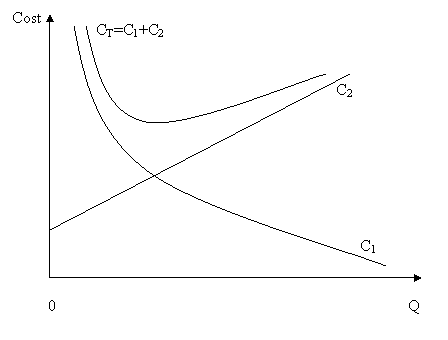 Figura 2
Figura 2
METODE DE REGLARE A STOCURILOR
Pornind de la modelul clasic determinist (modelul Wilson) al "cantitatii
economice", se pot defini doua principii fundamentale de reglare:
- Metoda punctului de comanda - se comanda cantitati
fixe optime, la momente de timp care pot sa varieze in functie
de cererea aleatoare.
- Metoda de aprovizionare periodica - se comanda dupa o
periodicitate data (in principiu aproape de periodicitatea
optima), cantitati care pot varia in functie de
cererea aleatoare.
A. Metoda punctului de comanda
Presupunem ca exista o intarziere in livrare, D, nealeatoare, (numita si timp de avans), care cuprinde: durata de
livrare impusa de furnizor, durata transportului, duratele administrative
(de redactare a comenzii, de receptie si luare in gestiune a
cantitatii intrate in stoc). Pentru
ca intrarea in stoc sa se faca la momentul de timp fixat, este
necesar ca lansarea comenzii sa se faca cu D unitati de timp in avans (Figura 3).
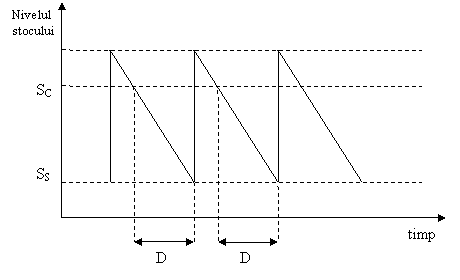
Figura 3
Daca nu se doreste sa fie afectat stocul de
siguranta (SS), nivelul
stocului in momentul lansarii comenzii va fi:
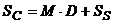 (3)
(3)
unde: M reprezinta viteza de
descrestere a stocului. Acest nivel (SC)
se numeste punct de comanda
si permite definirea celor doua principii ale metodei:
Se
lanseaza o noua comanda cand nivelul stocului devine inferior
sau egal punctului de comanda SC.
Se
comanda o cantitate fixa (QE),
care este cantitatea economica.
In cazul determinist, aceasta metoda conduce la evolutia
clasica a stocului, reprezentata de graficul "dinti de fierastrau". Dar, atunci cand cererea devine
aleatoare cele doua principii de gestiune constituie un mod de reglare
eficienta a stocului, prin stabilirea momentelor de lansare a comenzilor.
Exemplu. Se considera: QE = 6 unitati, SS
=1, PE = 3 luni
si D = 2 luni.
Punctul de comanda va fi conform relatiei (1):
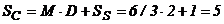
Presupunem ca la 15 zile
dupa aprovizionare se inregistreaza o cerere pentru o comanda
exceptionala de 2
unitati (Figura 4).
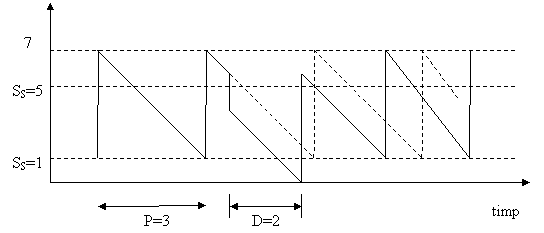
Figura 4
La acest moment stocul cade sub punctul
de comanda si se lanseaza o noua comanda de 6 unitati, care va intra in
stoc peste doua luni, adica cu 15
zile inainte de data normala de sosire. Stocul va urca la nivelul 6 unitati si apoi va
descreste cu viteza constanta M
= 2. In aceasta situatie punctul
de comanda va fi atins dupa 15
zile, iar livrarea se va face 2 luni
mai tarziu. Stocul va urca la nivelul de 7
unitati si se reia astfel ritmul normal de lansare a
comenzilor si de intrare a cantitatilor livrate in stoc.
Comentariu. Metoda punctului
de comanda permite rezolvarea fluctuatiilor cererii printr-o
stabilire corespunzatoare a momentelor de lansare a comenzilor. Astfel, in
exemplul prezentat doua cicluri de aprovizionare au o lungime de 2 luni si 15 zile in loc de 3 luni, dupa care se revine la
ritmul normal, cu un decalaj total de o luna. In acest sistem cantitatea
comandata ramane constanta, dar perioada de aprovizionare poate
varia in jurul perioadei economice (PE)
in functie de cerere. Aceasta metoda este cea mai eficace
si cea mai utilizata.
B. Metoda aprovizionarii periodice
Metoda consta in lansarea la date fixe a comenzii ce contine cantitati
variabile. Lansarea unei noi comenzi se va face dupa o perioada P, de la ultima lansare, in principiu
egala cu PE ( perioada economica, ciclul economic).
Sosirea comenzii in stoc se va face dupa o perioada D de la lansare. Ramane de stabilit pentru fiecare ciclu de aprovizionare,
marimea comenzii ce trebuie lansate.
Daca cererea nu este aleatoare, o comanda trebuie sa acopere
cererea pe durata unui ciclu de aprovizionare, deci:
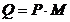 (4)
(4)
Stocul existent, (SE),
in momentul comenzii, trebuie sa permita satisfacerea cererii pe
durata timpului de avans, (D), adica:
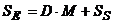 (5)
(5)
Daca apare o cerere aleatoare, este posibil ca stocul existent sa
nu atinga nivelul precedent. Sunt posibile doua situatii:
a) SE este mai mic
decat nivelul precedent - atunci comanda va fi marita pentru a
acoperi acest deficit. Valoarea comenzii va fi in acest caz:
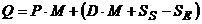 (6)
(6)
Rezulta 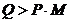 .
.
b) SE este mai mare
decat nivelul precedent - relatia (6) ramane valabila.
Rezulta 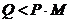 .
.
Concluzie. Valoarea comenzii Q va fi determinata pentru fiecare ciclu de
aprovizionare, astfel incat:
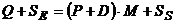 (6
(6
Expresia 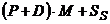 se numeste nivel de acoperire si are o valoare constanta.
Rezulta ca valoarea comenzii Q se determina in functie de stocul existent SE .
se numeste nivel de acoperire si are o valoare constanta.
Rezulta ca valoarea comenzii Q se determina in functie de stocul existent SE .
Exemplu. Se considera o aprovizionare
periodica cu: M = 2, SS
=1, P = 3 luni si D = 2 luni. Nivelul de acoperire este:
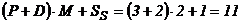
Presupunem ca la 15 zile
dupa aprovizionare se inregistreaza o cerere pentru o comanda
exceptionala de 2
unitati.
La momentul C2, marimea comenzii va fi Q = 11 - 3 = 8
unitati, pentru ca SE
=3. Doua luni mai tarziu, la
momentul L2, nivelul stocului devine dupa aprovizionare 7 unitati, presupunand ca
cererea nesatisfacuta de 1
nu s-a pierdut, ea fiind reportata. In C3 regasim valoarea
normala a comenzii Q = 6 unitati (Figura 5).
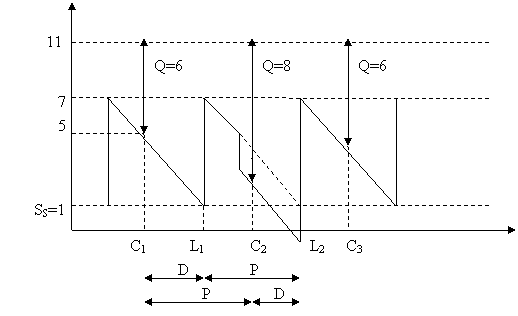
Figura 5
Comentariu. La aceasta metoda, graficul
aprovizionarii - momentul lansarii comenzii si momentul intrarii
in stoc sunt fixate, iar marimea comenzii se stabileste in
functie de fluctuatiile cererii.
DETERMINAREA STOCULUI DE
SECURITATE
Stocul de securitate permite evitarea situatiilor de lipsa de
stoc datorate unor cereri aleatoare sau unor intarzieri in livrare. In
continuare vom analiza determinarea stocului de securitate numai in cazul
cererilor aleatoare. Stocul de securitate se considera proportional
cu abaterea medie patrata a dispersiei cererii pe durata perioadei de
risc de ruptura. Coeficientul de proportionalitate va reflecta
calitatea serviciului cerut, care se poate defini in functie de unul din
parametrii urmatori: rata de ruptura de stoc, costul rupturii de
stoc, rata lipsei de stoc sau costul lipsei de stoc.
Presupunem ca cererea pe unitatea de timp este aleatoare si
urmeaza o distributie normala de medie M si abatere medie
patratica Pentru valori mici ale mediei ( M mai mic decat 7 sau 8) se poate considera distributia Poisson.
Daca se considera distributia normala, stocul de
securitate va fi dat de:
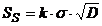 (7)
(7)
in cazul metodei punctului de
comanda si
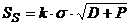 (8)
(8)
in cazul metodei aprovizionarii
periodice.
Observatie. In relatiile (7) si (8),
coeficientul k exprima calitatea
serviciului cerut si se numeste factor
de protectie sau rata
serviciului. Factorul k poate fi determinat pornind de la rata de
ruptura (sau riscul de ruptura) tR
, care este raportul dintre numarul de rupturi de stoc acceptate pe o
anumita perioada si numarul total de cicluri de
aprovizionare (sau de comenzi) desfasurate in aceeasi
perioada. Astfel, daca se accepta n rupturi de stoc intr-un an, vom avea: 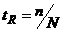 , unde N reprezinta numarul anual de comenzi.
, unde N reprezinta numarul anual de comenzi.
A. Determinarea stocului
de securitate in functie de rata de ruptura
A1. In cazul metodei punctului de comanda,
se inregistreaza o ruptura de stoc cand cererea pe durata D a timpului
de avans este mai mare decat stocul existent in momentul lansarii
comenzii, 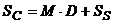 . Probabilitatea acestui eveniment va fi egala cu rata de ruptura tR ,
. Probabilitatea acestui eveniment va fi egala cu rata de ruptura tR ,
Prob (cererea pe D > MD + SS ) = tR (9)
In ipoteza ca marimea cererii pe durata D urmeaza o distributie normala 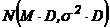 si ca stocul de
securitate este dat de relatia (7), factorul k va fi dat de:
si ca stocul de
securitate este dat de relatia (7), factorul k va fi dat de:
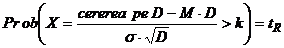 (10)
(10)
Rezulta ca:
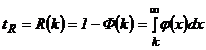 (11)
(11)
unde: 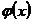 este densitatea de probabilitatea a distributiei
normale N(0,1), iar
este densitatea de probabilitatea a distributiei
normale N(0,1), iar
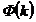 este functia lui
Laplace.
este functia lui
Laplace.
Exemplu. Presupunem ca pe o perioada de un an
s-au inregistrat urmatoarele cereri lunare (in unitati): 14, 11, 9, 10, 6, 12, 10, 11, 8, 9, 10, 10.
Rezulta:
valoarea
medie a cererii, M =10
dispersia
estimata, 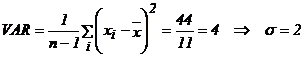
In ipoteza ca timpul de avans, D
= 4 luni si se accepta un risc de ruptura de 2.5%, se obtine stocul de siguranta: 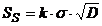 = 1.96 × 2 × 2 = 7.84 (aprox. 8 unitati)
= 1.96 × 2 × 2 = 7.84 (aprox. 8 unitati)
Punctul de comanda 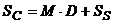 = 10 × 4 + 8 =48 unitati.
= 10 × 4 + 8 =48 unitati.
A2. In cazul metodei aprovizionarii periodice singura
modificare consta in valoarea stocului de siguranta, 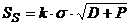 . Observam ca in cazul acestei metode stocul de
siguranta este mai mare pentru a putea obtine aceeasi
calitate a serviciului.
. Observam ca in cazul acestei metode stocul de
siguranta este mai mare pentru a putea obtine aceeasi
calitate a serviciului.
STUDIUL DE CAZ
Intreprinderea W
cumpara si stocheaza articolul A, pentru ca apoi sa-l
revanda cu un adaus comercial. Sa se stabileasca o politica
optima de aprovizionare care sa minimizeze costul total de gestiune a
stocului, in urmatoarele ipoteze initiale:
I1. Vanzarile sunt regulate;
I2. Cantitatea totala vanduta intr-un an este de 1800
unitati;
I3. Pretul unitar de
cumparare al articolului este de 1 u.m.;
I4. Costul de lansare a unei comenzi
este de 10 u.m.;
I5. Costul de stocare este 10% din
pretul articolului;
I6. Stocul de siguranta
are valoare nula.
A.
Sa se determine marimea lotului
economic si numarul optim de aprovizionari.
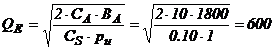 unitati
unitati
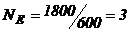 aprovizionari pe an
aprovizionari pe an
B. Furnizorul propune un rabat comercial (discont)
de 5% daca se comanda cel putin 900 de unitati. Se
accepta propunerea?
Daca se accepta remiza, intreprinderea va comanda cel putin 900 unitati. Aceasta revine la
lansarea a doua comenzi pe an (1800 , sau o singura
comanda de 1800
unitati.
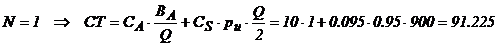
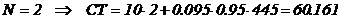
Rezulta ca se accepta propunerea de remiza cu doua
comenzi pe an de volum 900 unitati.
C. Intreprinderea W decide sa accepte
propunerea de discont si va comanda de 2 ori pe an cate 900 unitati.
Din experienta, cererea pe o perioada de 6 luni variaza
dupa o lege normala N(900,902). Sa se calculeze
probabilitatea de ruptura de stoc daca intreprinderea constituie un
stoc de siguranta de volum 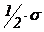 . Care va fi probabilitatea in cazul unui stoc de
siguranta de volum
. Care va fi probabilitatea in cazul unui stoc de
siguranta de volum 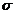 ? Determinati volumul stocului de
siguranta necesar pentru o rata a serviciului de 95%.
? Determinati volumul stocului de
siguranta necesar pentru o rata a serviciului de 95%.
Cu un stoc de siguranta SS
unitati, ruptura de stoc se produce
daca cererea pe 6 luni, 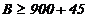 unitati. Se
obtine:
unitati. Se
obtine:
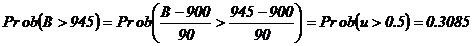
unde u are o repartitie N(0,1).
Deci, riscul de ruptura de stoc este de 30%, iar rata serviciului este de 70%.
Daca stocul de siguranta este egal cu 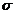 rezulta:
rezulta:
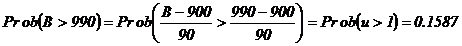
Deci, riscul de ruptura de stoc este de 15%, iar rata serviciului este de 85%.
Daca se doreste o rata a serviciului de 95% avem:
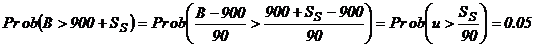
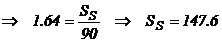
APLICAREA SIMULARII LA GESTIUNEA STOCURILOR
Tehnica de simulare Monte Carlo ne permite sa obtinem valori
artificiale ale cererii si eventual ale duratelor de livrare, conform
distributiilor de probabilitate observate. Utilizand aceste valori
artificiale in cadrul unei metode de gestiune, se pot calcula diversi
parametrii: rata de ruptura, costul rupturii, etc. Va fi deci posibil
sa comparam diverse metode de gestiune.
Tehnica de simulare Monte Carlo ne permite sa abordam diverse
scenarii de gestiune a stocurilor, care pot diferi de metodele clasice ale punctului de comanda sau al aprovizionarii periodice.
A. Obtinerea unui
esantion artificial al cererii
Metoda Monte Carlo permite
obtinerea unui esantion cu o distributie de probabilitate
data, plecand de la un esantion de numere aleatoare uniform repartizate
pe intervalul (0,1).
Fie X o variabila aleatoare discreta, cu
distributia:
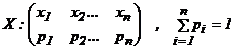
Algoritmul de generare al variabilei X
este:
Pasul 1. Se calculeaza 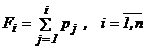 .
.
Initializam: i = 0
Pasul 2. Se genereaza U uniform repartizat pe (0,1).
Pasul 3. Se calculeaza: i = i
Pasul 4. Daca U > Fi atunci transfer la Pasul 3.
Pasul 5. Iesire X = xi . Stop.
Exemplu. Consideram cazul unui distribuitor
care gestioneaza stocul unui produs. El inregistreaza cererea aleatoare
a produsului si constata ca probabilitatea p(n) a unei cereri zilnice de n articole este conforma cu tabelul
urmator:
|
Cererea zilnica
N
|
|
|
|
|
|
|
|
|
|
Probabilitatea
p(n)
|
|
|
|
|
|
|
|
|
|
Fi
|
|
|
|
|
|
|
|
|
Dorim sa obtinem o serie aleatoare a cererii zilnice conform cu
aceasta distributie de probabilitate. De exemplu, daca valorile
variabilei aleatoare uniforme U sunt: 0.29,
0.59, 0.93, aplicand algoritmul se obtin valorile cererii zilnice: 2, 3, 6 articole. Am redus astfel
problema generarii unor cereri zilnice cu o anumita distributie
de probabilitate, la generarea unor numere aleatoare repartizate uniform in
intervalul [0,1].
B. Simularea stocului pentru
o metoda de gestiune data
Definim o metoda de gestiune foarte simpla: se comanda in
ultima zi lucratoare a saptamanii (care are 5 zile
lucratoare), un numar de articole egal cu consumul mediu al unei
saptamani.
Media cererii este egala cu:
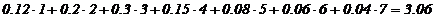
Deci, cererea saptamanala este de 15 articole. Se
presupune in plus, ca stocul initial este egal cu 15 articole.
Se obtine evolutia urmatoare a stocului calculata la
sfarsitul fiecarei zile, stiind ca in cazul lipsei de stoc
cererea nesatisfacuta nu se reporteaza pentru ziua
urmatoare.
unde: Z = ziua
C
= cererea
S
= stocul la sfarsitul zilei
P = penurie
Efectuand simularea pentru 100 zile
lucratoare s-a calculat cererea totala exprimata, penuria
totala si numarul de zile de stocare/articol.
Observatie. Trebuie adaugate zilele de stocare de
la sfarsitul saptamanii; de exemplu pentru prima saptamana
se obtine:
15D+15L+9M+7M+4J+15V+15S
= 80 zile/articol de
stocare.
Rezulta:
- cererea totala: 317
- numarul de zile/articol
de stocare: 1540
- penuria totala: 21
- rata de penurie: 21
/ 317 = 6.6%
Daca se presupune ca avem un cost de stocare de 1 u.m. / articol / zi, costul de
reaprovizionare este neglijabil, iar costul unitar al lipsei de stoc este de 50 u.m. , va rezulta un cost total pentru 100 zile de:
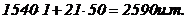
Concluzie. Acest cost va putea fi comparat cu cel
rezultat din aplicarea altor reguli de reaprovizionare. Totusi, pentru ca
rezulatatele obtinute sa fie stabile trebuie efectuate simulari
pentru o perioada de cel putin 300
de zile.



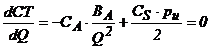
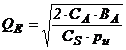 (2)
(2)



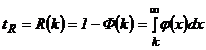 (11)
(11)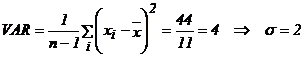
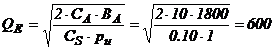
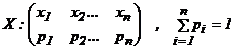
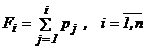 .
.