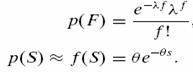Cuprins:
Introducere . . . . . . . . . . . . . . . . . . . 3
Retele
bayesiene . . . . . . . . . . . . . . . . . 5
Estimarea
pierderilor asteptate si neasteptate . . . . 6
Folosirea retelelor bayesiene pentru previzionarea
pierderilor . . . . . . . . . . . . . . . . . . . ..8
Previzionarea
pierderilor totale din frecventa si severitatea evenimentelor
Modelarea
dependentelor dintre frecventa si severitatea evenimentelor
Concluzii . . . . . . . . . . . . . . . . . . . ..13
Bibliografie . . . . . . . . . . . . . . . . . . ..13
Introducere
Aceasta lucrare
descrie folosirea retelelor bayesiene pentru modelarea distributiilor
statistice ale pierderilor in scenarii de risc financiar operational. Ne vom
concentra asupra modelarii evenimentelor de pierdere neasteptata(cu "coada
lunga") folosind combinatii de distributii adecvate ale frecventei si
severitatii pierderilor, unde aceste combinatii sunt conditionate de variabile
cauzale ce modeleaza randamentul sau eficacitatea procesului comenzilor de
baza. Utilizarea modelarii cauzale
este discutata din perspectiva exploatarii expertizei locale in legatura cu fiabilitatea
proceselor si a asocierii formale dintre aceste cunostinte si fenomenele
statistice reale sau ipotetice rezultate din procese. Aceasta abordare aduce
avantajul suplimentarii datelor incomplete cu parerile expertilor si
transformarii cunostintelor calitative despre procese in predictii cantitative.
Retelele bayesiene ajuta in combinarea intr-un mod inteligent a datelor
calitative obtinute de la experti si a datelor cantitative din baze de date ce
retin istoricul pierderilor si astfel intrunesc intr-o masura insemnata
conditiile Acordului Basel II (Basel, 2004) pentru o abordare avansata a
masuratorilor(AMA - advanced measurement aproach).
Comitetul Basel pentru Supervizarea
Bancara, ca reactie la un numar de dezastre financiare foarte mediatizate, a
creat un sistem de regularizare tratand problema riscului operational(OpRisk)
si a evaluarii sale. Esential pentru procesul de regularizare este modelarea
riscurilor operationale ale afacerii, ca varietate a tipurilor de evenimente de
pierdere, pentru a obtine o adecvare corecta a capitalului propriu. Pentru calcularea unei asemenea ajustari
este tentant sa se previzioneze riscul operational construind un model
statistic bazat pe date istorice. Totusi, din perspectiva statistica,
dezastrele financiare in sine, cum ar fi Barings si Allied Irish Bank, sunt
prea putine ca numar pentru orice inferenta semnificativa. Mai mult, pana de
curand, bancile nu au inregistrat cronologic date despre evenimentele de
pierdere la o scara larga si in mod sistematic. Aceasta insuficienta generala a
datelor despre pierderi inseamna ca este improbail ca abordarile statistice
traditionale sa ofere predictii utile referitoare la pierderile operationale. O
imbinare de metode cantitative si calitative este necesara pentru a modela
riscurile operationale.
Problema OpRisk nu este particulara pentru
sectorul financiar si riscul operational nu este un subiect nou. In cartea sa,
James Reason, argumenteaza ca riscul operational este intampinat de toate
organizatiile si foloseste exemple din sectoarele financiar, transport
feroviar, aviatie civila si centrale nucleare pentru a-si sustine afirmatiile.
Reason identifica o multime de motive datorita carora au loc esecuri
catastrofice in cadrul acestor industrii in care siguranta este un element
critic, printre care se numara(dar nu sunt singurele) incapacitatea de a insusi
lectiile invatate din esecurile anterioare, degradarea inceata sau prabusirea
procedurilor de siguranta, schimbari in cultura si management, lipsa viziunii
si a structurii pentru raportarea riscurilor si a lipsei de atentie la detalii.
Concluzia este ca accidentele nu sunt rezultatul exclusiv al failibilitatii
umane, ci sunt datorate si caracteristicilor organizatiei care nu reuseste sa
se apere impotriva greselilor umane inerente, neatentiilor si (in cazul
fraudei) a actelor rau intentionate. Putem spune ca predictia riscurilor
operationale este strans legata de un bun management si ca masurarea OpRisk
poate fi semnificativ facuta doar daca eficacitatea proceselor de control al
riscului sunt evaluate regulat. Aceasta viziune contrasteaza puternic cu ideea
ca modelarea OpRisk implica doar investigarea fenomenelor statistice.
Datorita acelorasi argumente, catastrofele
financiare nu sunt "un fulger venit din senin" si nu sunt nici inexplicabile.
Scandalurile financiare ca Barings si AIB au fost toate rezultatul
activitatilor frauduloase acumulate de-a lungul unor perioade indelungate, timp
in care un management activ le-ar fi putut identifica si preveni. Exista o tendinta
de a vedea dezastrul financiar ca un singur eveniment de tip "pierdere foarte
ridicata", in locul unei agregari de pierderi mai mici sporite in timp, ceea ce
este de inteles avand in vedere ca pierderile sunt inregistrate la descoperire,
toate odata. Dar acest lucru nu schimba faptul ca astfel de pierderi sunt
acumulate zilnic si pot fi detectate printr-o atentie sporita inglobata in
rutina. Orice sistem de riscuri operationale ar trebui, deci, sa se concentreze
asupra detectarii micilor pierderi in fiecare luna sau trimestru inainte ca
acestea sa devina piederi importante sau dezastre.
In aceasta lucrare se incearca argumentarea
faptului ca retelele bayesiene reprezinta o solutie atragatoare pentru
problemele identificate mai sus. Retelele bayesiene ne permit combinarea
oricaror date statistice disponibile cu date calitative si judecati subiective
asupra proceselor. Asadar retelele bayesiene furnizeaza metode de modelare a
pierderilor operationale si de masurare a eficacitatii proceselor operationale
ale unei firme ca parte a unei abordari orientate pe auto-evaluare.
Folosind
retelele bayesiene putem:
Combina indicatori proactivi ai
pierderilor, legati de desfasurarea afacerii, cu masurari reactive ale
rezultatelor precum succes incomplet(near miss) si date despre pierderi.
Incorpora parerile expertilor cu privire la
contributia pe care o pot avea estimatorii calitativi asupra evaluarii riscului
general.
Introduce dovezi incomplete si totusi sa obtinem
predictii
Realiza analiza de tipul "what-if" puternica
pentru a testa senzitivitatea concluziilor
Obtine o unealta vizuala de rationare si un
ajutor important in documentare
Obtine output sub forma predictiilor
verificabile relativ la masuratorile performantelor reale si ratele
evenimentelor de pierdere.
In capitolul 2 vom oferi o privire de
ansamblu asupra retelelor bayesiene. In capitolul 3 vom trata diferentele larg
acceptate dintre pierderile asteptate si cele neasteptate in riscurile
operationale, iar in capitolul 4 vom explica cum retelele bayesiene ofera o
medota unificata de prezicere a ambelor tipuri de pierderi. Ne vom concentra
asupra problemei esentiale de previzionare a pierderilor folosind doua retele
bayesiene pentru a arata cum pot fi utilizate pentru modelarea frecventei,
severitatii evenimentelor de pierdere si a distributiilor cu "coada lunga"
(heavy-tailed). Capitolele 5 si 6 cuprind concluziile, respectiv bibliografia.
Retele bayesiene
Teoria de baza a retelelor bayesiene
combina probabilitatea bayesiana si notiunea de independenta conditionala
pentru a reprezenta dependentele dintre variabile (Pearl, 1986; Speigelhalter
& Cowell, 1992). Pana in prezent retelele bayesiene s-au dovedit utile in
multe tipuri de aplicatii ca sisteme expert medicale, de diagnostic al
esecurilor, corespondenta tiparelor, recunoasterea vocala si, mai relevant
pentru comunitatea riscurilor operationale, evaluarea riscurilor sistemelor
complexe in medii cu miza ridicata.
Retelele bayesiene(Bayesian
Networks - BN) fac posibila analiza in conditii de incertitudine si combina
avantajele unei reprezentari vizuale intuitive cu o baza matematica solida in
probabilitatea bayesiana. Cu BN putem utiliza cunostintele expertilor in
legatura cu dependentele dintre diferite variabile si sa proiectam in mod
consistent impactul dovezilor asupra probabilitatilor rezultatelor incerte. BN
permit o insuflare de rigurozitate stiintifica cand distributiile de
probabilitate asociate nodurilor individuale sunt doar "opiniile expertilor".
Acest lucru poate sa creasca increderea in parerile expertilor, subliniind in
acelasi timp imprecizia inerenta in asemenea tipuri de judecati.
O retea bayesiana
este un graf orientat ale carui noduri reprezinta variabilele(discrete) incerte
de interes si ale carui muchii sunt legaturile cauzale sau de influenta dintre
variabile. Fiecarui nod i se asociaza un tabel de probabilitati. Acesta este un
set de probabilitati conditionate ce modeleaza relatia de incertitudine dintre
nod si parintele sau.
Cheia unui design de
succes al retelelor bayesiene este descompunerea corecta a domeniului problemei
intr-un set de propozitii cauzale sau conditionale despre domeniu. In loc sa
cerem unui expert intreaga distributie unificata de probabilitati, care este
evident o sarcina foarte dificila, putem aborda o strategie de tipul
"divide-et-impera" si sa cerem detalii partiale ale modelului care au
semnificatie in domeniul expertului. Obtinand aceasta descompunere, am
specificat, ca rezultat natural al abordarii, si covarianta prin structura
probabilitatilor conditionate.
In continuare avem
nevoie ca expertul sa alcatuiasca tabelul probabilitatilor nodului(TPN) pentru
fiecare variabila(nod): acest lucru poate fi facut fie utilizand date
cronologice (prin invatarea parametrica bayesiana standard sau simularile Monte
Carlo), fie cerand expertului sa furnizeze o serie de estimari subiective. Ideal ar fi ca aceste estimari sa se
bazeze pe experienta si cunostinte, nu pe presupunere oarba.
Putem introduce cu usurinta distributii
statistice discrete si continue in cadrul modelului retelei bayesiene, ca
tabele de probabilitati ale nodurilor, si genera valori pentru aceste TPN-uri
prin simulari Monte Carlo. Pentru functii continue trebuie sa aducem modelul la
valori discrete corespunzatoare si in software-ul AgenaRisk aceasta operatie
este realizata folosind o versiune avansata a algoritmului de discretizare
dinamica prezentat in Kozlov si Koller (1997), permitand aproximarea solutiei
atat pentru problemele statistice bayesiene clasice, implicand variabile
continue, cat si pentru problemele hibride ce implica atat variabile discrete
cat si continue.
Odata construita
reteaua bayesiana, aceasta poate fi executata folosind un algoritm de propagare
adecvat cum ar fi algoritmul arborelui de jonctiune. Acest lucru presupune
calcularea tabelei unificate a probabilitatilor din structura probabilitatilor
conditonate ale BN intr-o maniera eficienta. Pentru aceasta se deriveaza
automat din BN reprezentarea unui graf teoretic, intermediar, numit arbore de
jonctiune care permite executarea calculelor locale, modulare folosind un
algoritm de transmitere a mesajelor. In esenta aceasta este o forma elaborata a
teoremei lui Bayes. Intregul proces este complet automat, iar intr-un
instrument ca AgenaRisk este ascuns expertului in domeniu.
Odata ce reteaua bayesiana a fost
compilata, aceasta poate fi executata dinamic si prezinta urmatoarele doua
caracteristici:
Efectele
observatiilor introduse in unul sau mai multe noduri pot fi propagate in
intraga BN, in orice directie, si distributiile marginale ale tuturor nodurilor
sunt actualizate.
Doar
inferentele relevante pot fi facute in BN. Reteaua bayesiana foloseste
structura dependentelor conditionale si cunostintele curente pentru a determina
acele inferente care sunt valide.
Este important de observat ca volumul si
complexitatea calculului implicate in folosirea retelelor bayesiene pot fi
controlate din punct de vedere a memoriei interne si spatiului de stocare daca
se foloseste o implementare eficienta a algoritmului arborelui de jonctiune.
Totusi, multe pachete academice, open-source nu ofera implementari care sunt
suficient de eficiente pentru a suporta modele mari de retele bayesiene, mai
ales combinate cu simularea Monte
Carlo. Dar implementari eficiente sunt posibile pentru
clasa de retele bayesiene necesare modelarii problemelor de risc operational si
pot fi asamblate relativ usor in unelte ca AgenaRisk.
Estimarea pierderilor asteptate si neasteptate
Raportul Basel clasifica pierderile
financiare datorate factorilor operationali in doua categorii:
Pierderi
asteptate - acestea sunt considerate pierderi "normale" ce apar frecvent, ca
parte a functionarii zilnice, cu o severitate redusa. Un exemplu ar fi
pierderile datorate greselilor accidentale de calcul a ratelor internationale
de schimb.
Pierderi
neasteptate - sunt pierderile neobisnuite care apar rar si au severitate
sporita (Ex: pierderi rezultate dintr-o activitate frauduloasa majora).
Figura 1 arata
deosebirea dintre pierderile asteptate si cele neasteptate. Linia de demarcare
este pur arbitrara(in figura, aceasta separare apare pentru pierderi totale de
$400000). In concluzie nu are sens sa folosim metode fundamental diferite
pentru previzionarea pierderilor asteptate si neasteptate; este mai util sa
gandim in sensul gasirii unei distributii a carei coada reprezinta pierderile
neasteptate.
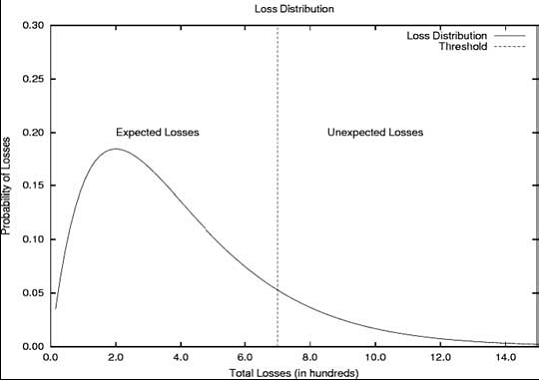
Fig. 1. Pierderi totale
asteptate fata de cele neasteptate
Abordarea traditionala a acestui tip de
probleme este ca gasirea distributiei previzionate sa se bazeze doar pe date
cronologice. Unde exista date din abundenta, tehnicile de modelare statistica
traditionala functionaza bine, insa in cazul datelor referitoare la pierderi
operationale exista o serie de probleme speciale. Cea mai importanta este ca,
chiar atunci cand exista o cantitate mare de date despre pierderi, este
improbabil ca vor exista date suficiente despre pierderile neasteptate
insemnate pentru a putea estima in mod corect coada distributiei - de obicei
rezulta cozi care sunt prea "subtiri" sau prea "groase" daca datele despre
pierderi nu sunt relevante pentru domeniul in cauza. Chiar in modelarea
pierderilor asteptate (grosul distributiei), abordarea orientata spre date
sufera din cauza urmatoarelor limitari:
Datele despre pierderi vor fi culese pe o perioada de
timp ce ar putea reprezenta nivele variate ale eficacitatii operationale si
riscului. Nu ne putem astepta ca pierderile sa fie generate de o singura
distributie cu un numar mic de parametri "cunoscuti".
Pierderile suferite exprima doar un
esantion de evenimente posibile. Ar putea fi nereprezentative in conditiile
proceselor operationale in schimbare. In masura in care procesul operational de
baza se degradeaza sau imbunatateste, valoarea unor astfel de date cronologice
scade.
Datele raportate despre pierderi ar putea
fi gresite. Raportarea incompleta si ambiguitatea datelor pot duce la erori
semnificante in estimare.
Orice incercare de sustinere a datelor
despre pierderi cu informatii culese de la alte organizatii este supusa
acelorasi probleme si nu numai, deoarece foarte des provenienta datelor este
necunoscuta sau incerta.
Folosirea retelelor
bayesiene pentru previzionarea pierderilor
Datorita limitarilor serioase ale
abordarilor bazate doar pe date cronologice este inevitabila utilizarea
metodelor care ne permit incorporarea altor tipuri de dovezi. Acolo unde
trebuie combinate tipuri diferite de dovezi metodele statistice clasice nu
functioneaza. Metodele
bayesiene, si in particular retelele bayesiene, reprezinta o modalitate
eficienta deoarece ofera urmatoarele beneficii in OpRisk:
Combinarea explicita a datelor obiective
si subiective prin modelare conexiunilor dintre mediul operational si
procesului de pierdere.
Pot modela distributii cu "coada lunga"
pentru componenta de pierdere neasteptata din totalul distributiei pierderilor.
O metoda de extragere de la experti a
componentelor subiective de previzionare a riscului prin modelarea explicita a
scenariilor care implica diferite procese operationale sau riscuri asupra
firmei, cu rezultate probabile.
Un mijloc verificabil de a trata expertiza
in asa fel incat modelele pot fi ulterior folosite independent de expert in
acelasi fel in care sistemele expert medicale pot sustine practicieni mai putin
calificati punand la dispozitie sfaturi "experte".
In acest capitol vom
descrie doua modele de retele bayesiene pentru previzionarea pierderilor
operationale. Primul previzioneaza pierderile totale din frecventa si
severitatea evenimentelor presupunand ca acestea sunt independente. Al doilea
presupune o dependenta intre frecventa si severitate.
Previzionarea
pierderilor totale din frecventa si severitatea evenimentelor
Putem estima distributia
totala a pierderilor din convolutia distributiilor frecventei si severitatii
pierderilor unde pierderile totale, T, sunt conditionate de frecventa pierderilor,
F, si severitatea acestora in caz ca apare. Frecventa si
severitatea evenimentului de pierdere sunt variabile aleatoare, fiecare cu o
functie a densitatii probabilitatii(fdp) specifica. Pentru o frecventa a evenimentului de
pierdere data, F, si o distributie a severitatii, S, vrem sa previzionam
distributia totala a pierderilor, T. Distributia unificata a probabilitatilor
p(F, S, T) = p(T| F,S)p(S)p(F), iar distributia totala a pierderilor este
calculata marginalizand F si S, deci: 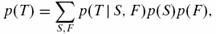
p(F,S,T) putand fi reprezentata grafic de
o retea bayesiana ca in figura 2.
Datorita faptului ca retelele
bayesiene faciliteaza folosirea metodelor Monte Carlo
pentru generarea tabelelor de probabilitati, nu este necesar sa restrictionam
modelul nostru la nici o familie data de distributii conjugate de
probabilitate. Pentru simplitate fdp pentru frecventa evenimentelor
poate fi reprezentata cel mai bine de distributii cu un singur parametru. Vom folosi o distributie Poisson, cu
parametrul ratei λ, si o distributie exponentiala, cu parametrul θ,
ca distributia severitatii apriori cunoscuta, S.
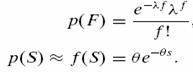 Astfel:
Astfel:
Folosind AgenaRisk putem
genera p(T| F,S) esantionand S si F utilizand metode Monte Carlo si calculand
pierderile totale, T, pentru fiecare combinatie de S si F esantionate.
Odata ce reteaua bayesiana a
fost specificata si TPN-urile generate, putem calcula probabilitatea marginala
a fiecarui nod din BN invocand algoritmul de propagare.
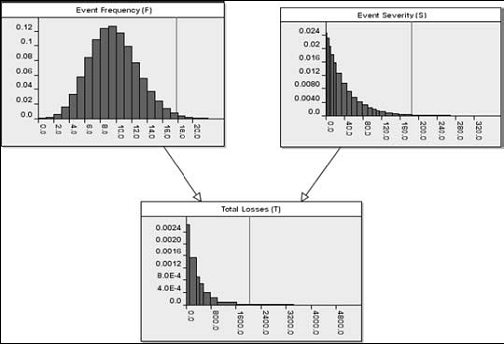
Fig.2. BN pentru p(F, S,
T) aratand distributiile marginale aposteriori pentru fiecare variabila.
Luand in considerare presupunerile noastre, avem nevoie de estimatori cu un
singur parametru pentru perechea ( ) pentru a genera
p(F, S, T). Sa presupunem ca, din experienta anterioara obtinuta de
la un expert, rata medie a pierderilor pe an este aproximativ 10, = 9.7 si
severitatea medie a pierderilor este $40000 per eveniment de pierdere, cu Atunci distributia
aposteriori rezultata pentru p(T), calculata de BN apare ca in figura 3.
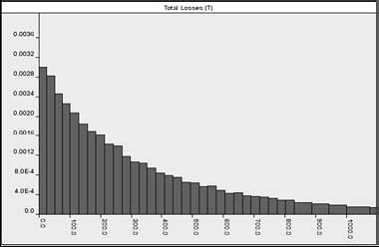
Fig.3.
Distributia marginala aposteriori pentru p(T), unde T<1000
Modelarea
dependentei dintre frecventa si severitatea evenimentelor
Modelul de mai sus presupune ca frecventa
si severitatea evenimentului de pierdere sunt independente. In realitate ne
putem astepta ca ele sa covarieze cel putin pentru anumite clase de evenimente
cum ar fi frauda, unde ne-am putea astepta ca un proces de control slab sa
incurajeze un hot sa fure mai mult decat un proces de control eficient. Pentru
alte clase de evenimente dependentele ar putea fi mai slabe. Putem modela usor
covarianta dintre severitatea S si frecventa F, introducand o cauza comuna, pe
care o vom numi eficienta procesului,
E, in modelul retelei bayesiene. Noua distributie unificata de probabilitati
p(F,S,T,E) = p(T| F,S)p(S|E)p(F|E)p(E). Aceasta este reprezentata grafic de BN
din figura 4. Putem compara acest model de dependenta, conditionat de E, cu
varianta independenta discutata anterior, comparand direct distributiile
marginale aposteriori pentru T in cazurile de dependenta respectiv
independenta:
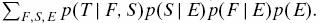 si
si
Pentru a ilustra cel mai bine diferentele
dintre modele, putem construi un model folosind valori medii pentru p(S) si
p(F) care sunt foarte apropiate de modelul orginal de independenta. Amestecul
de TPN-uri ales ca exemplu este reprezentat in tabelul 1.
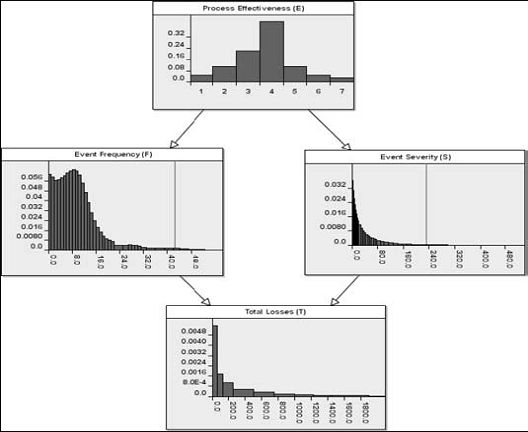
Fig.4. BN pentru
p(F,S,T,E) aratand distributiile marginale aposteriori pentru fiecare
variabila, unde F si S sunt conditionate de E.

Tabelul 1. TPN-uri pentru p(E), p(F|E) si p(S|E)
Asteptarile pentru frecventa evenimentului, F, si severitatea, S, sunt usor
derivate din reteaua bayesiana. Acestea sunt aproape identice cu cele utilizate
cand F si S sunt independente: E(F) = 10 si E(S) = 40. Totusi, problema se
refera la forma cozii lui p(T), sau formulata ca intrbare: Pierderile
neasteptate sunt mai mari cand F si S covariaza?
Figura 5 arata coada functiilor de densitatea a probabilitatii pentru
valori ale lui T>1000, iar tabelul 2 arata o comparatie a mediei si a
procentului 99(putem atribui procentul 99 ca masura Valoareii de Risc(VaR -
Value at Risk)) cand F si S sunt independente respectiv dependente. Se poate
observa ca atunci cand F si S sunt dependente obtinem o coada mai lunga decat
atunci cand sunt independente. Aceasta diferenta a cozilor este evidentiata si
de catre diferentele dintre valorile procentului 99 pentru T: in cazul
dependentei valoarea este 4.937, iar in cazul independentei, 1.933. Deci in caz de independenta valoarea VaR
va fi optimista.
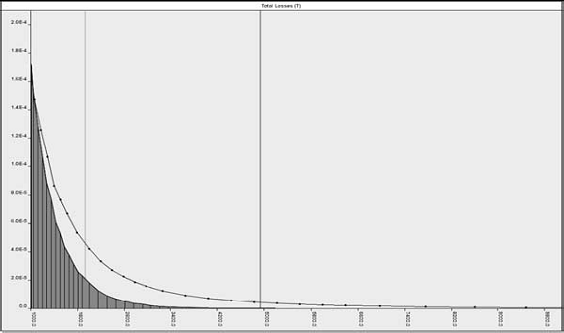
Fig.5. Comparatie
cozilor distributiilor pierderilor totale. Zona
gri inchis arata cazul de independenta, iar linia neagra arata cazul de
dependenta.
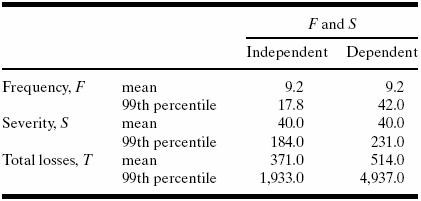
Tabelul 2. Statistici pentru medie si procentul 99 pentru F, S si T in
cazurile de dependenta si independenta.
Concluzii
Retelele
bayesiene ajuta in combinarea intr-un mod inteligent a datelor calitative
obtinute de la experti si a datelor cantitative din baze de date ce retin
istoricul pierderilor si astfel intrunesc intr-o masura insemnata conditiile
Acordului Basel II (Basel, 2004) pentru o abordare avansata a masuratorilor(AMA
- advanced measurement aproach). Abordarea
bazata pe retele bayesiene ar trebuie sa duca, in consecinta, la o mai buna guvernare
a riscului operational si la o ajustare a capitalului propriu scazuta. Bazarea
doar pe datele cronologice despre pierderi si tehnicile de analiza statistica
traditionala nici nu va duce la predictii corecte ale viitoarelor pierderi din
riscuri operationale, si nici nu va furniza un mecanism pentru monitorizarea si
controlul unor asemenea pierderi.
Am aratat cum retelele bayesiene pot fi folosite
pentru a modela riscul operatioal prin doua exemple in care pierderile totale
sunt bazate pe frecventa si severitatea evenimentelor. In cel de-al doilea
model am luat in considerare posibila dependenta dintre frecventa si severitate
prin introducerea unei cauze comune - eficienta
procesului - si am aratat ca putem folosi aceasta retea bayesiana pentru a
modela distributii cu "coada lunga" intr-un mod care ar exploata experienta
disponibila intr-o organizatie. Aceasta ajuta la estimarea unei VaR
realiste si reproductibile.
Retelele
bayesiene se concentreaza asupra estimarii eficacitatii procesului de baza al
afacerii si am propus folosirea lor ca o forma de auto-analiza, implicand
monitorizarea desfasurarii afacerii in mod frecvent si translatarii acestor
note din auto-analiza in predictii asupra pierderilor totale cu ajutorul
retelelor bayesiene.
Bibliografie
Marten Neil,
Norman Fenton, Manesh Tailor - Risk
Analysis, vol. 25
David Heckerman
- A tutorial on learning with Bayesian
Networks
Richard E.
Neapolitan - Learning Bayesian Networks