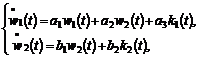Modele liniare
Modelele liniare
prezentate in continuare sunt in general constituite cu ajutorul
ecuatiilor sau al sistemelor de ecuatii algebrice, diferentiale
sau cu diferente finite si de limiteaza la descrierea
fenomenului respectiv.
Modelul
trimestrial de investitii al lui Eisner.
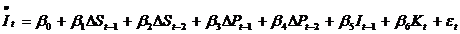 ,
,
unde 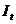 - investitia,
- investitia, 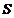 - economiile in societate,
- economiile in societate,
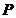 - profiturile (
- profiturile (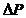 - modificari profituri ),
- modificari profituri ), 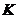 - fonduri capitale
existente la inceputul perioadei. Sa observam ca ecuatia
acestui model este cu argument intarziat, deci acesta este infinit dimensional.
- fonduri capitale
existente la inceputul perioadei. Sa observam ca ecuatia
acestui model este cu argument intarziat, deci acesta este infinit dimensional.
Model cerere-oferta
Este un
model studiat de Beckmann si Ryder in 1969 si de Collel in 1986.
Acest model prezinta reactia pe care pretul 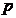 o produce asupra
cantitatii
o produce asupra
cantitatii 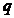 si invers. El este
dat de
si invers. El este
dat de
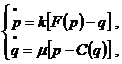
unde 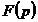 - excesul de cerere
iar
- excesul de cerere
iar 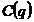 - costul lui
- costul lui 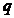 . De obicei
. De obicei 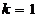 si
si 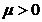 este un parametru.
Pretul creste ca raspuns la excesul de cerere
este un parametru.
Pretul creste ca raspuns la excesul de cerere 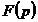 sau cantitatea
sau cantitatea 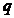 descreste in
raport cu costul
descreste in
raport cu costul 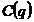 .
.
Model de crestere cu capital uman
Acest
model neoclasic simplu, in care capitalul uman are un rol crucial, a fost propus
de Mankiw si contine o functie de productie de tip
Cobb-Douglas
 .
.
Modelul
descrie o evolutie economica si are forma
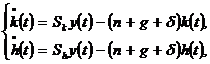
unde 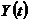 - functia de productie,
- functia de productie, 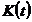 - stocul de capital fizic,
- stocul de capital fizic, 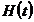 - stocul de capital uman,
- stocul de capital uman, 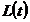 - forta de munca presupusa
crescatoare cu rata
- forta de munca presupusa
crescatoare cu rata 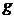 si cantitatile pe unitatea de
munca sunt
si cantitatile pe unitatea de
munca sunt 

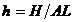
Politici de stabilizare
Fluctuatiile economiei pot fi tinute sub control prin varierea
cheltuielilor guvernamentale 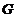 , ori de cate ori acestea scad brusc fata de un
nivel dorit
, ori de cate ori acestea scad brusc fata de un
nivel dorit 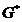 , adica
, adica 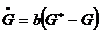 , unde
, unde 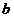 este constanta
pozitiva ce reprezinta viteza de ajustare. Phillips si Allen
disting trei tipuri de nivele de cheltuieli guvernamentale
este constanta
pozitiva ce reprezinta viteza de ajustare. Phillips si Allen
disting trei tipuri de nivele de cheltuieli guvernamentale 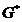 si anume:
si anume:
a) 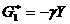 , cand venitul national cumulat scade brusc sub nivelul
dorit
, cand venitul national cumulat scade brusc sub nivelul
dorit 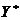 presupus egal cu zero
pentru simplicitate;
presupus egal cu zero
pentru simplicitate;
b) 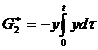 , cand venitul national cumulat scade de asemenea sub un
nivel
, cand venitul national cumulat scade de asemenea sub un
nivel 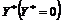 ;
;
c) 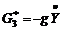 , cand cheltuielile guvernamentale scad odata cu
cresterea venitului.
, cand cheltuielile guvernamentale scad odata cu
cresterea venitului.
Tinand
seama ca venitul national brut creste odata cu excedentul
cererii globale 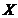 fata de
oferta globala
fata de
oferta globala  , pentru politicile de stabilizare obtinem trei modele
diferite corespunzatoare celor trei tipuri de cheltuieli guvernamentale.
, pentru politicile de stabilizare obtinem trei modele
diferite corespunzatoare celor trei tipuri de cheltuieli guvernamentale.
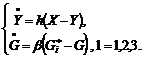
Model pentru productivitatea muncii
Sa consideram sistemul dinamic afin ce descrie corelatia
intre dinamica productivitatii muncii 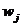 , inzestrarea tehnica a muncii
, inzestrarea tehnica a muncii 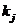 , la doua sucursale ale unei firme producatoare de
autoturisme
, la doua sucursale ale unei firme producatoare de
autoturisme
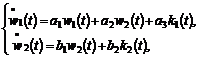
cea de-a doua sucursala livrandu-i primeia o serie
de subansamble.
Se
cunosc starile initiale: 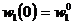 (mii lei/persoana) - productivitatea
medie lunara,
(mii lei/persoana) - productivitatea
medie lunara, 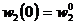 (mii lei/persoana) - inzestrarea
tehnica a muncii
(mii lei/persoana) - inzestrarea
tehnica a muncii 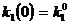
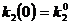
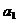
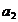
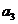
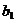
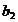 - parametri constanti.
- parametri constanti.
Ciclul comercial al lui Samuelson (1939)
Modelul lui Samuelson este construit cu ajutorul unui multiplicator si
accelerator. Consumul curent 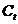 este o functie
liniara descrescatoare de venitul
este o functie
liniara descrescatoare de venitul  pe o anumita
perioada
pe o anumita
perioada 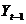 iar investitia
curenta
iar investitia
curenta 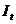 creste cu
cresterea consumului
creste cu
cresterea consumului 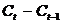 . Mai precis
. Mai precis 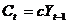
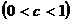 ,
, 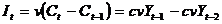
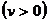 ,
, 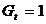 (nivelul cheltuielilor
guvernamentale),
(nivelul cheltuielilor
guvernamentale), 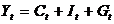 ,
,  .
.
Cei doi parametri ai
modelului sunt  - multiplicator
si
- multiplicator
si 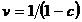 - accelerator.
- accelerator. 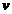 reprezinta viteza
de raspuns a lui
reprezinta viteza
de raspuns a lui 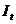 la cresterea
consumului. Prin substitutie se obtine o ecuatie
functionala algebrica
la cresterea
consumului. Prin substitutie se obtine o ecuatie
functionala algebrica
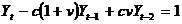 , (
, (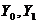 - dati)
- dati)
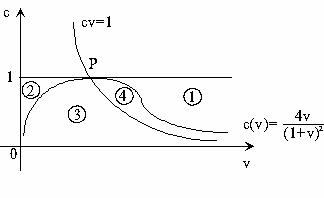
- Fig.4.2 -
a carei solutie este 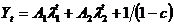 , unde
, unde 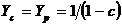 este o solutie
particulara iar constantele
este o solutie
particulara iar constantele  si
si 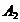 au expresii in care
apar
au expresii in care
apar 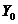 si
si 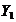 . Ecuatia caracteristica a ecuatiei omogene in
. Ecuatia caracteristica a ecuatiei omogene in
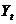 este
este 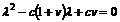 si are
radacinile
si are
radacinile  . Cei doi parametri
. Cei doi parametri  si
si 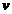 determina
stabilitatea lui
determina
stabilitatea lui 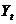 , in functie de natura si semnele lui
, in functie de natura si semnele lui 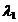 si
si 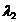 , deci de cele trei cazuri in care determinantul
, deci de cele trei cazuri in care determinantul 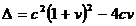 este pozitiv, nul sau
negativ. Astfel, in cazul radacinilor complexe (
este pozitiv, nul sau
negativ. Astfel, in cazul radacinilor complexe ( ) solutia
) solutia 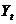 este periodica.
In cazul
este periodica.
In cazul  avem ca
avem ca 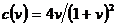 este o functie
concava pentru
este o functie
concava pentru 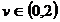 , care isi atinge maximul in
, care isi atinge maximul in 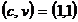 . La
. La 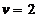 ,
, 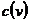 are un punct de
inflexiune si apoi devine convexa, adica
are un punct de
inflexiune si apoi devine convexa, adica 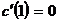 ,
, 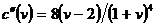 si
si 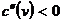 pentru
pentru 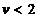 ,
, 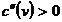 pentru
pentru 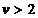 . Sub curba
. Sub curba 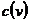 radacinile
radacinile 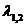 sunt reale si
distincte implicand o descrestere monotona a lui
sunt reale si
distincte implicand o descrestere monotona a lui 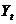 (adica
fara fluctuatii) iar deasupra ei radacinile sunt
complexe indicand fluctuatii. Pe curba
(adica
fara fluctuatii) iar deasupra ei radacinile sunt
complexe indicand fluctuatii. Pe curba 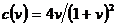 solutia este
solutia este 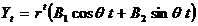 , unde
, unde 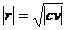 . Ea este stabila daca
. Ea este stabila daca 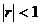 si instabila
daca
si instabila
daca 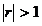 . In loc de stabila (instabila) se mai zice
convergenta (divergenta). Astfel, cele doua curbe
. In loc de stabila (instabila) se mai zice
convergenta (divergenta). Astfel, cele doua curbe 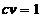 si
si 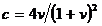 impart spatiul
parametrilor in 4 zone de comportament diferit ale lui
impart spatiul
parametrilor in 4 zone de comportament diferit ale lui 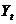 : monoton divergenta (1), periodic divergenta (2),
periodic convergenta (3) si monoton convergenta (4). Acestea
completeaza ciclul lui Samuelson. In plus, s-a considerat doar semibanda
: monoton divergenta (1), periodic divergenta (2),
periodic convergenta (3) si monoton convergenta (4). Acestea
completeaza ciclul lui Samuelson. In plus, s-a considerat doar semibanda 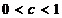 ,
,  in care
in care  si
si 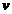 au sens economic.
au sens economic.
omogena in diferente 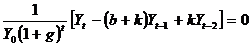 se reduce la o
ecuatie omogena in diferente in
se reduce la o
ecuatie omogena in diferente in 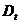 ,
, 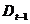 ,
, 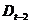 si arata
ca
si arata
ca 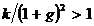 este conditia de
instabilitate.
este conditia de
instabilitate.
Modelul
mai poate fi extins prin considerarea comertului exterior, importurile
fiind functii de venit: 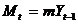
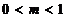 . Exporturile sunt determinate de cererea
externa, care se presupune a creste cu o rata
proportionala constanta
. Exporturile sunt determinate de cererea
externa, care se presupune a creste cu o rata
proportionala constanta 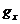 , astfel ca
, astfel ca 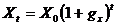


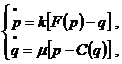
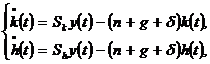
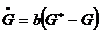 , unde
, unde 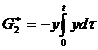 , cand venitul national cumulat scade de asemenea sub un
nivel
, cand venitul national cumulat scade de asemenea sub un
nivel