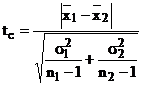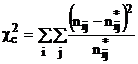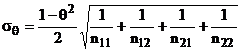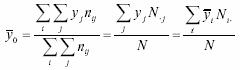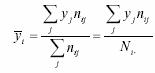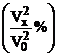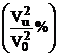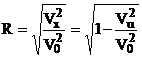Utilizarea testelor statistice la fundamentarea
deciziilor econometrice
1. Asocierea a
doua variabile alternative
2 Asocierea a
doua variabile calitative nealternative
3 Asocierea dintre o variabila alternativa independenta
si o variabila numerica dependenta
4 Asocierea a
doua variabile numerice
- Testul diferentei
dintre doua medii
Acest test consta in
compararea valorii empirice a variabilei tc cu valoarea sa
teoretica ta
unde:
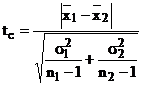
ta este argumentul
distributiei normale, daca n 30 , sau argumentul distributiei
Student, daca n < 30 ;
a este pragul de
semnificatie (riscul) cu ajutorul caruia se alege decizia corecta;
de regula, in economie se lucreaza cu un prag de semnificatie de
0,05 (5%) sau, cel mult, de 0,01 (1%).
Se intalnesc urmatoarele
situatii:
daca tc < ta rezulta
ca intre cele doua variabile x1 si x2 nu
se poate accepta o diferenta semnificativa;
daca tc ta rezulta
ca intre cele doua variabile x1 si x2 se
poate accepta o diferenta semnificativa.
Acest test consta in
compararea valorii empirice a variabilei c c cu valoarea sa teoretica c a n
unde:
c c se calculeaza dupa relatia: 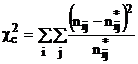
nij sunt
frecventele reale
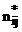 sunt frecventele teoretice in cazul independentei totale a celor
doua variabile
sunt frecventele teoretice in cazul independentei totale a celor
doua variabile
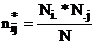
a este pragul de
semnificatie
n = (k-1)(m-1) este
numarul gradelor de libertate, m fiind numarul de grupe in
functie de variabila Y= , iar k este numarul de grupe in functie
de variabila X
Utilizarea
testului c se bazeaza pe
urmatoarele reguli de decizie:
daca c c < c a n , rezulta ca cele
doua variabile X si Y sunt independente;
daca c c c a n , rezulta ca cele
doua variabile X si Y nu sunt independente;
- In cazul unei grupari
combinate de 2x2, adica 2 variabile care au 2 variante, analiza
statistica a legaturii dintre acestea se poate face si cu
ajutorul coeficientului de asociere al lui Yulle, definit prin
relatia:
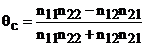
Acest coeficient
este definit in intervalul qI , avand semnificatia:
q 1 corelatie strict negativa intre
variabile;
q 0 independenta intre variabile;
q 1 corelatie strict pozitiva intre
variabile.
cu abaterea medie
patratica:
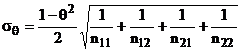
Stiind ca
variabila q este o variabila aleatoare
ce urmeaza o distributie normala N q ), valoarea empirica qc se accepta ca este
semnificativ diferita de zero daca 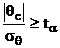 , rezulta ca intre cele doua variabile
exista o legatura, iar daca
, rezulta ca intre cele doua variabile
exista o legatura, iar daca 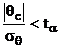 rezulta ca
valoarea lui qc nu este semnificativ
diferita de zero, ceea ce presupune ca cele doua variabile sunt
independente.
rezulta ca
valoarea lui qc nu este semnificativ
diferita de zero, ceea ce presupune ca cele doua variabile sunt
independente.
- Metoda analizei
variatiei
Metoda analizei variatiei se
fundamenteaza pe discutia urmatoarelor distributii:
distributia marginala a variabilei Y
distributiile conditionate ale variabilei Y in functie de
variantele variabilei factoriale X
Pe baza acestor distributii
se calculeaza trei marimi:
- variatia
totala 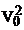 (sau dispersia
totala
(sau dispersia
totala 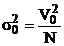 ), calculata pe baza distributiei marginale a lui Y
cu ajutorul relatiei:
), calculata pe baza distributiei marginale a lui Y
cu ajutorul relatiei:
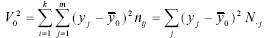
unde:
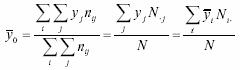
reprezinta
media distributiei marginale, iar 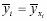 sunt mediile conditionate ale variabilei
Y in functie de variantele variabilei factoriale X.
sunt mediile conditionate ale variabilei
Y in functie de variantele variabilei factoriale X.
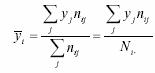
Aceasta
marime, 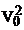 , masoara variatia totala a variabilei Y
generata de influenta intregului complex de factori ce o
determina.
, masoara variatia totala a variabilei Y
generata de influenta intregului complex de factori ce o
determina.
- varianta
dintre grupe 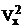 este masura
variatiei variabilei Y generata de variatia caracteristicii
factoriale X. Aceasta marime se calculeaza cu relatia:
este masura
variatiei variabilei Y generata de variatia caracteristicii
factoriale X. Aceasta marime se calculeaza cu relatia:
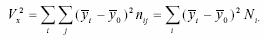
- varianta
reziduala 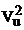 este o marime
care exprima variatia caracteristicii Y generata de factorii
considerati aleatori, exceptand influenta factorului X. Relatia
de calcul a acestei marimi este:
este o marime
care exprima variatia caracteristicii Y generata de factorii
considerati aleatori, exceptand influenta factorului X. Relatia
de calcul a acestei marimi este:
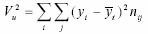
Se poate demonstra ca intre
cele trei marimi exista relatia:
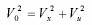
Raportand
relatia de mai sus la 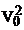 se obtine contributia relativa a factorului
esential X
se obtine contributia relativa a factorului
esential X 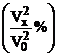 si a factorilor
intamplatori u
si a factorilor
intamplatori u 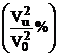 la explicarea
variatiei totale.
la explicarea
variatiei totale.
Indicatorul 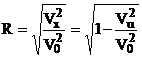 poarta numele de raport de
corelatie empirica si exprima intensitatea legaturii
dintre cele doua variabile.
poarta numele de raport de
corelatie empirica si exprima intensitatea legaturii
dintre cele doua variabile.
Se deduce usor ca acest
indicator este definit in intervalul
Interpretarea
valorilor raportului de corelatie empirica se face pe baza
urmatoarelor reguli:

Daca datele
provin dintr-o cercetare selectiva, inainte de a explica variatia lui
Y si a interpreta valoarea raportului de corelatie empirica va
trebui sa se verifice semnificatia rezultatelor. Testarea
semnificatie rezultatelor se face cu ajutorul testului "F" - testul Fisher-Snedecor.
Rezultatele se
considera semnificative (R este semnificativ diferit de zero) daca exista inegalitatea:
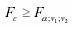
unde:

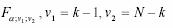 este valoarea teoretica
preluata din tabela distributiei Fisher-
este valoarea teoretica
preluata din tabela distributiei Fisher-
Snedecor in
functie de un prag de semnificatie si de numarul gradelor de libertate v si v
1. Asocierea a
doua variabile alternative
O societate
comerciala se aprovizioneaza de la 2 furnizori A si B. Dupa
primirea ultimelor doua loturi de piese se stie ca:
- furnizorul A a trimis 400 de
piese din care 60 au fost rebuturi;
- furnizorul B a trimis 600 de
piese din care 70 au fost rebuturi.
Conducerea
societatii ar dori sa renunte la furnizorul A pe motivul
unei calitati inferioare a produselor sale in raport cu cele ale
furnizorului B.
Este corecta aceasta
decizie?
Rezolvare:
Pas1. Se
sistematizeaza datele intr-un tabel:
|
Furnizor (X)
|
Calitatea
pieselor (Y)
|
Total
|
|
Rebuturi
|
Bune
|
|
A
|
|
|
|
|
B
|
|
|
|
|
Total
|
|
|
|
unde:
X - variabila
independenta cu:
x1 - furnizorul A
x2 - furnizorul B
Y - variabila
dependenta cu:
y1 - piese rebut
y2 - piese bune
Decizia poate fi
luata pe baza a trei procedee statistice: testul diferentei dintre
doua medii, testul c si coeficientul de asociere Yulle.
Testul
diferentei dintre doua medii (Testul t)
Pas. 2
Se
poate folosi fie programul Microsoft Excel (prag de semnificatie a
Pas. 2.1 Se apeleaza comanda fx
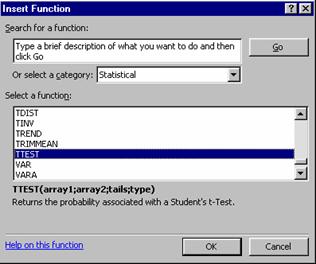 Pas. 2.2 Din categoria de functii
statistice, se alege functia TTEST
Pas. 2.2 Din categoria de functii
statistice, se alege functia TTEST
Pas. 2.3
Sau se poate folosi programul EViews
Pas. 2.1 Se introduc datele
(Quick _ Empty Group sau preluate din Excel)
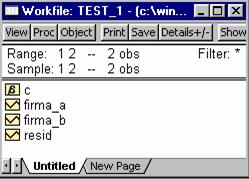
Pas. 2.2 Se selecteaza cele doua variabile "firma_a" si
"firma_b" pentru a putea fi vizualizate:
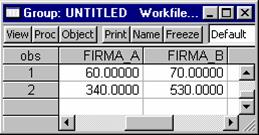
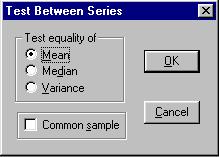
Pas. 2.3 Din meniul View se alege comanda Tests of Equality si optiunea Mean
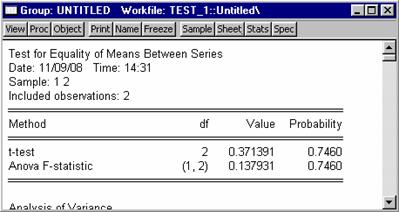 Pas. 2.4 S-au obtinut rezultatele:
Pas. 2.4 S-au obtinut rezultatele:
Pas.3 Se alege pragul de semnificatie a si se preia valoarea
acestuia din tabelul distributiei respective; pentru a 0,05, din tabela distributiei normale se preia valoarea t0,05
=
Pas.4 Deoarece tc < t0,05 rezulta
ca intre calitatea pieselor livrate de cei doi furnizori, cu o
probabilitate de 0,95 (95%), nu se poate accepta o diferenta
semnificativa si, ca atare, nu este corecta decizia de a se
renunta la furnizorul A pe motivul unei mai slabe calitati a
pieselor.
Probleme propuse
Intr-o sectie de prelucrare a unei
intreprinderi exista doua prese (A si B), pe fiecare din ele
prelucrandu-se cate un lot de piese de acelasi tip.
Datorita diminuarii cererii
acestui produs intreprinderea trebuie sa renunte la una din prese.
Sa se mentioneze la care presa trebuie sa se renunte
cunoscand urmatoarele rezultate obtinute in urma unei selectii:
- dintr-un lot de 1000 de piese executate
la presa A, 2,5% au fost rebuturi;
- dintr-un lot de 800 de piese executate la
presa B, 4,5% au fost rebuturi.
Testul c
Pas. 2
Se
poate folosi fie programul Microsoft Excel
Pas. 2.1 Se calculeaza frecventele
teoretice
|
Furnizor
|
Bune
|
Rebut
|
Total
|
|
A
|
|
|
|
|
B
|
|
|
|
|
Total
|
|
|
|
|
frecvente
teoretice
|
|
|
|
|
|
|
|
|
|
|
Pas. 2.2 Se apeleaza comanda fx
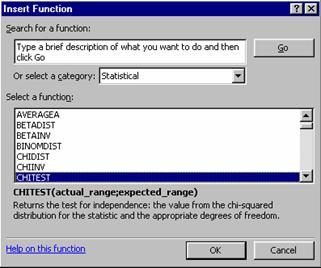
Pas. 2.3 Din categoria de functii statistice,
se alege functia CHITEST
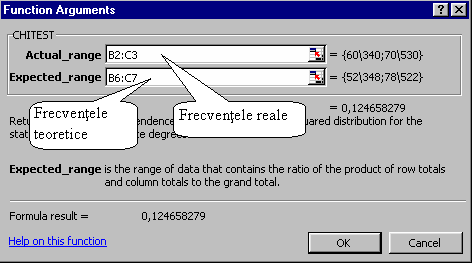 Pas. 2.4
Pas. 2.4
Sau se poate folosi programul EViews
Pas. 2.1 Se introduc datele

Pas. 2.2 Se selecteaza cele doua variabile "firma_a" si
"firma_b" pentru a putea fi vizualizate:

Pas. 2.3 Consideram ca cele doua variabile sunt independente
si atunci din meniul View se alege comanda N-Way Tabulation
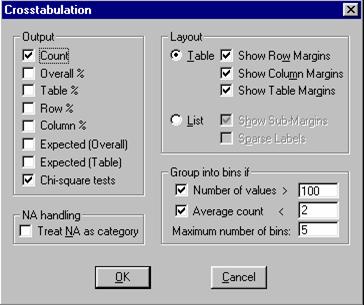
Pas. 2.4 S-au obtinut rezultatele:
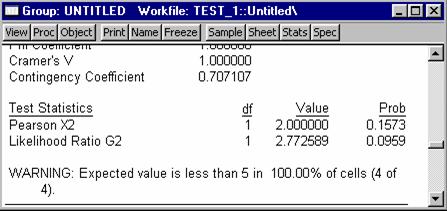
Pas.3 Cele doua variabile sunt
independente, deci calitatea pieselor nu depinde de tipul furnizorilor si,
ca atare, nici decizia de a rezilia contractul cu furnizorul A nu este
justificata.
2 Asocierea a
doua variabile calitative nealternative
In urma
efectuarii unui sondaj statistic s-au obtinut urmatoarele date
privind distributia pe ramuri ale economiei nationale a
somerilor, grupati pe trepte de calificare:
|
Ramuri ale
economiei (X)
|
Trepte de calificare a
somerilor (Y)
|
Total
|
|
Necalificati
|
Calificare
medie
|
Calificare
superioara
|
|
Industrie
|
|
|
|
|
|
Constructii
|
|
|
|
|
|
Alte ramuri
|
|
|
|
|
|
total
|
|
|
|
|
Analizati datele din tabel
si precizati daca se poate admite o asociere intre profilul
ramurilor economice si calificarea somerilor.
Rezolvare:
Datele problemei se
refera la dependenta dintre doua variabile nominale X - ramurile
economiei nationale) si Y - trepte de calificare ale somerilor
ale caror variante sunt in numar mai mare de doua - cazul unui
tabel de k m rubrici.
In acest caz,
acceptarea sau respingerea ipotezei de dependenta statistica
dintre cele doua variabile se poate face cu ajutorul testului c