Conductibilitatea termica a gazelor

Conductibilitatea termica a gazelor

Fenomenul de conductibilitate termica consta in transportul caldurii ΔQ de pe un strat aflat la o temperatura T₁, mai mare, spre un alt strat aflat la temperatura T₂ < T₁ (fig. 7.6). Problema conductibilitatii termice a fost tratata de matematicianul si fizicianul francez Jean Baptiste Fourier (1768-1830) in lucrarea ,,Teoria analitica a caldurii'', aparuta in anul 1822. Legea conductibilitatii termice, stabilita de Fourier, poate fi enuntata astfel: caldura ΔQ care trece prin elementul de arie ΔS, in intervalul de timp Δt, este proportionala cu gradientul de temperatura ΔT/ Δx, cu aria Δ si cu intervalul de timp Δt:

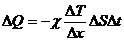   (7.22)

Coeficientul de proportionalitate χ reprezinta coeficientul de conductibilitate termica, numit mai pe scurt conductivitatea termica a substantei in care se produce transmiterea caldurii. Formulele (7.20) si (7.22) sunt analoage, deoarece conductibilitatea termica are loc ca si cum caldura ar "difuza" din straturile cu temperatura mai inalta catre straturile cu temperatura mai mica. Conductivitatea termica χ a unei substante este numeric egala cu caldura care strabate in unitatea de timp o suprafata de arie egala cu unitatea, cand de o parte si de alta a acestei suprafete exista un gradient de temperatura egal cu unitatea.

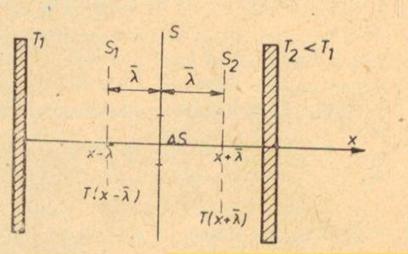
Fig.7.6. Reprezentarea schematica a procesului de conductibilitate termica

Daca temperatura unui gaz este diferita in diferite puncte din volumul acesteia, atunci si energia cinetica medie a moleculelor gazului (vezi relatia 6.1)

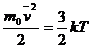
va avea valori diferite in diferite puncte. Deplasandu-se dintr-un loc in altul, moleculele transporta energia acumulata. Procesul conductibilitatii termice este conditionat de acest transport de energie. In intervalul de timp Δt, prin elementul de arie ΔS va trece in ambele sensuri un numar N de molecule, unde:

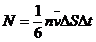  (7.23)

Am considerat ca pe o distanta egala cu 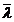, moleculele au aceeasi viteza medie 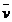in ambele parti ale planului S (fig. 7.6). Aceasta aproximare poate fi admisa, deoarece temperaturile T(x-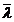) si T(x +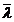) sunt foarte apropiate , iar viteza medie 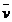este proportionala cu radacina patrata din temperatura T.

Pe baza formulelor (6.1) si (7.23), putem scrie expresia caldurii transmise prin aria ΔS, de la stratul S₁, la stratul S₂, in intervalul de timp Δt:

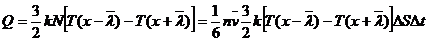(7.24)

Daca in planul S temperatura gazului este T, atunci in virtutea faptului ca drumul liber mediu 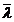este relativ mic, putem scrie:

;

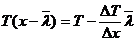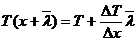(7.25)

Introducand expresiile (7.25) in formula (7.24) obtinem:

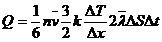
sau

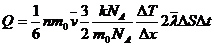    (7.26)

Produsul m₀n reprezinta densitatea ρ a gazului, iar

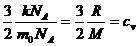    (7.27)

este caldura specifica a gazului in procesele izocore.

Asadar, formula (7.26) poate fi scrisa sub forma:

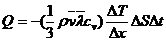(7.28)

Comparand formulele (7.22) si (7.28), obtinem expresia conductivitatii termice a gazelor ideale:

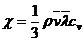(7.29)

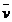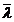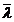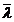Aceasta formula exprima legatua dintre marimea macroscopica χ si marimile fundamentale si , in teoria cinetico moleculara. Densitatea ρ fiind proportionala cu presiunea p a gazului, iar drumul liber fiind invers proportional cu presiunea p, produsul ρ este independent de presiune. Astfel, dupa formula (7.29), conductivitatea χ ar trebui sa fie independenta de presiune. Se constata insa ca aceasta concluzie nu este valabila pentru gaze rarefiate, adica pentru presiuni foarte mici.