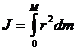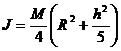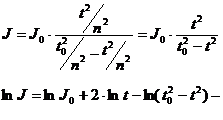Determinarea momentului de inertie si a modulului de forfecare cu pendulul de torsiune

1. Introducere teoretica :

Momentul de inertie al unui corp fata de o axa este definit de relatia:

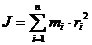(1)

unde m_i este masa unui punct material oarecare al corpului, r distanta punctului la axa si n numarul punctelor.

In majoritatea cazurilor practice corpurile pot fi considerate medii continue si (1) se calculeaza prin trecerea la limita pentru o infinitate de puncte materiale, cu mase infinit de mici, obtinandu-se:

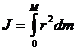
(2)

M fiind masa corpului.

Daca corpul se suspenda de un fir elastic, de exemplu de o sarma, aceasta poate efectua oscilatii de torsiune, constituind un pendul de torsiune. Oscilatiile sunt determinate de fortele elastice din fir.

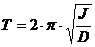Consideratiile teoretice permit exprimarea perioadei de oscilatie prin formula: (3)

unde:

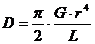
(4)

L fiind lungimea firului, r raza lui si G modulul de forfecare al materialului din care este confectionat firul.

Formula (3) permite calculul lui J in functie de T si D. Dar cunoasterea lui D poate fi evitata, daca se ataseaza corpului un alt corp de moment de inertie cunoscut. In aceasta situatie (3) devine:

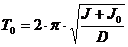(5)

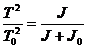Eliminand pe D din (3) si (5) prin impartirea acestor relatii se obtine:

(6)

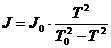si

(7)

MODUL DE LUCRU

Corpul al carui moment de inertie trebuie determinat, este un cilindru circular care poate fi prins de fir prin insurubare in doua pozitii (Fig. 1a. si 1b.). Corpul de moment de inertie cunoscut este o bara metalica care se prinde tot prin insurubare de partea inferioara a cilindrului (Fig. 2a. si 2b.).

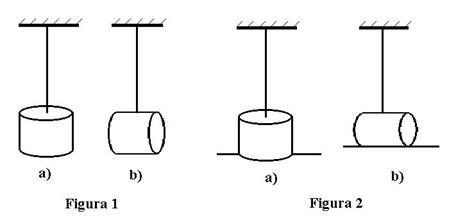
La inceput se fixeaza cilindrul din pozitia (Fig 1a.) si se masoara cu ctronometrul timpul t a n oscilatii, din care se obtine perioada T prin impartire cu n. Apoi se prinde bara ca in (Fig. 2a.), determinandu-se in acelasi fel T₀. Se repeta aceste operatii si pentru pozitiile din (Fig. 1a. si 2b.). Stiind ca J₀=4,4 lo^-4 kg m², se calculeaza in ambele cazuri J cu formula (7). Momentul de inertie al cilindrului poate fi calculat pe cale teoretica, obtinandu-se formulele:

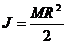pentru pozitia din (Fig. 1a.) 

(8)

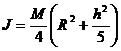
pentru pozitia din (Fig. 1b.)     (9)

in care R si h sunt raza si inaltimea cilindrului, iar M masa lui. Ele se masoara cu sublerul, respectiv cu balanta.

3. Prelucrarea datelor experimentale

Dupa calcularea momentelor de inertie cu formulele (8) si (9), rezultatele se trec in tabel la coloana J_teor, comparandu-se aceste rezultate cu cele experimentale din coloana J.

Inlocuind pe J din (7) in (3) se obtine:

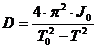(10)

iar din (4) se determina modulul de forfecare al firului:

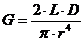
(11)

Valorile lui D si G trebuie sa coincida in limita erorilor, in ambele pozitii a. si b.

Eroarea relativa minima cu care s-a determinat momentul de inertie, se calculeaza astfel:

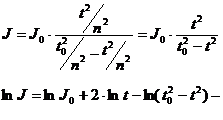
(12)

(13)

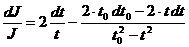
(14)

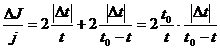Cum insa t si t₀ se determina cu acelasi cronometru, precizia este aceeasi si putem inlocui pe dt₀ cu dt. Pentru eroarea relativa liniara toate diferentialele, inclusiv cele cu semnul minus se inlocuiesc cu +Dt:

(15)

Pentru eroarea relativa limita a modulului de forfecare se gaseste in mod analog:

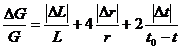(16)

4. concluzii

Se trag concluzii cu privire la valorile   obtinute cu aceasta metoda