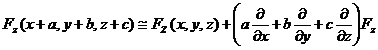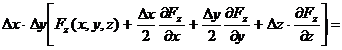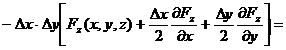Divergenta unei functii vectoriale
Fie 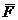 o functie
vectoriala oarecare in spatiul tridimensional;
o functie
vectoriala oarecare in spatiul tridimensional; 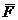 are in fiecare punct
din spatiu o directie si o marime bine definita.
are in fiecare punct
din spatiu o directie si o marime bine definita.
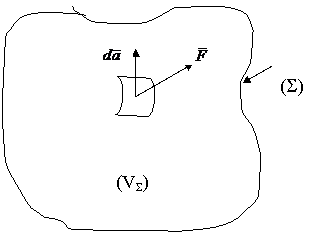
Se considera un volum finit (VS) de forma oarecare, a carui suprafata se noteaza
cu (S
Fluxul total al functiei vectoriale 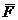 prin suprafata (S) este:
prin suprafata (S) este:
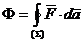 (A.4.6)
(A.4.6)
unde 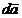 este un vector infinitezimal a carui marime este
egala cu aria unui element al suprafetei (S), iar directia coincide cu normala exterioara la acest element
de suprafata (fig. A.4.1).
este un vector infinitezimal a carui marime este
egala cu aria unui element al suprafetei (S), iar directia coincide cu normala exterioara la acest element
de suprafata (fig. A.4.1).
Fig.A.4.1.
Se divizeaza
volumul (VS) intr-un numar mare de portiuni de volume: 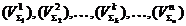 cu suprafetele
care le delimiteaza
cu suprafetele
care le delimiteaza 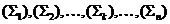 . Indiferent de numarul portiunilor:
. Indiferent de numarul portiunilor:
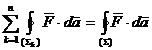 ,
(A.4.7)
,
(A.4.7)
deoarece
suprafetele comune pentru doua portiuni vecine (alaturate)
au contributii egale la flux dar de semn opus. Pentru a demonstra aceasta,
se considera ca volumul (VS) este
delimitat in doua portiuni de volume 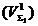 si
si 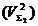 , cu:
, cu:
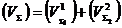 (A.4.8)
(A.4.8)
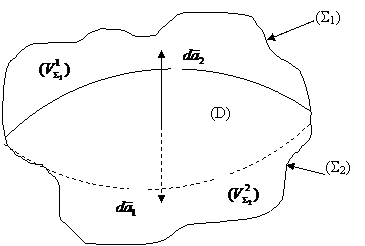 si fie (D) suprafata de separatie a celor doua
portiuni (fig.A.4.2).
si fie (D) suprafata de separatie a celor doua
portiuni (fig.A.4.2).
Fig.A.4.2.
Intrucat:
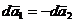
rezulta:
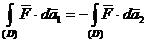 (A.4.9)
(A.4.9)
si atunci:
 . (A.4.10)
. (A.4.10)
La limita, cand n , vrem sa gasim ce este caracteristic pentru o portiune
foarte mica si, in final, pentru vecinatatea unui punct. In
acest sens se considera raportul:
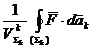 (A.4.11)
(A.4.11)
si se observa
ca pe masura ce are loc divizarea in mai multe parti a
volumului 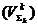 , care implica divizarea integralei in mai multi
termeni, raportul (A.4.11) tinde catre o limita. Aceasta
limita este o proprietate caracteristica a functiei vectoriale
, care implica divizarea integralei in mai multi
termeni, raportul (A.4.11) tinde catre o limita. Aceasta
limita este o proprietate caracteristica a functiei vectoriale 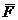 in vecinatatea
punctului continut in volumul
in vecinatatea
punctului continut in volumul 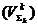 , numita divergenta
lui
, numita divergenta
lui 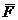 , adica:
, adica:
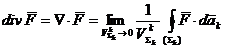 (A.4.12)
(A.4.12)
unde (Sk) este suprafata ce delimiteaza volumul 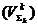 si pe care se ia integrala de suprafata.
si pe care se ia integrala de suprafata.
Din (A.4.12), 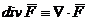 este fluxul
functiei vectoriale
este fluxul
functiei vectoriale 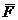 pe unitatea de volum
prin suprafata (Sk) ce margineste volumul
pe unitatea de volum
prin suprafata (Sk) ce margineste volumul 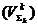 , pentru
, pentru 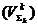 infinit de mic. Aceasta este o marime scalara de
coordonate.
infinit de mic. Aceasta este o marime scalara de
coordonate.
Trebuie introdusa insa, conditia ca limita
din relatia (A.4.12) sa existe si sa fie independenta
de modul de divizare.
Se demonstreaza, in continuare, ca in
coordonate carteziene, divergenta functiei 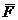 are expresia:
are expresia:
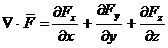 (A.4.13)
(A.4.13)
Se presupune o functie vectoriala 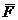 care este
exprimata in coordonate carteziene x,
y si z. Exista, deci,
trei functii scalare Fx(x,y,z);
Fy(x,y,z) si Fz(x,y,z)
astfel incat:
care este
exprimata in coordonate carteziene x,
y si z. Exista, deci,
trei functii scalare Fx(x,y,z);
Fy(x,y,z) si Fz(x,y,z)
astfel incat:
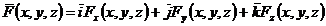 (A.4.14)
(A.4.14)
Se
considera un volum (Vk) de forma unui paralelipiped cu unul din
colturi in punctul de coordonate (x,y,z)
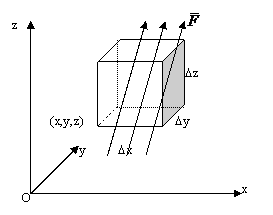
si cu laturile de lungime Dx, Dy si Dz (fig.A.4.3). Consideram
doua fete opuse ale paralelipipedului, de exemplu cele din planul z=const. Fluxul prin aceste
suprafete se datoreaza numai componentei Fz a functiei 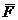 pe directia z si contributia finala
depinde doar de diferenta intre valoarea medie a lui Fz pe suprafata superioara si valoarea
medie a lui Fz pe
suprafata inferioara. Pentru a obtine aceasta
diferenta se are in vedere faptul ca valorile medii pe cele
doua suprafete (in prima aproximatie) sunt valorile
functiilor in centrul suprafetelor (fig. A.4.4) si se
foloseste aproximatia liniara a dezvoltarii in serie
Taylor:
pe directia z si contributia finala
depinde doar de diferenta intre valoarea medie a lui Fz pe suprafata superioara si valoarea
medie a lui Fz pe
suprafata inferioara. Pentru a obtine aceasta
diferenta se are in vedere faptul ca valorile medii pe cele
doua suprafete (in prima aproximatie) sunt valorile
functiilor in centrul suprafetelor (fig. A.4.4) si se
foloseste aproximatia liniara a dezvoltarii in serie
Taylor:
Fig.
A.4.3.
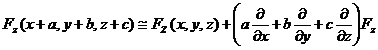 (A.4.15)
(A.4.15)
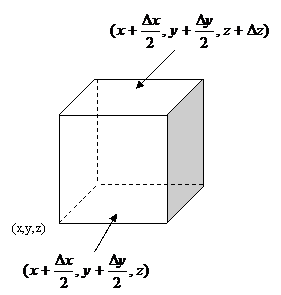
Fig.A.4.4.
Valoarea medie a lui Fz pe suprafata inferioara
este:
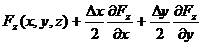 ,
,
iar pe suprafata
superioara:
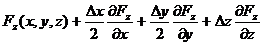 .
.
Fluxul total ce iese din paralelipiped prin cele
doua suprafete a caror arie este xy este egal cu:
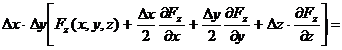
(fluxul ce iese prin
suprafata superioara)
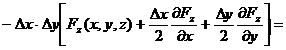
(fluxul ce intra
prin suprafata inferioara)
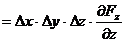 .
.
Aplicand acelasi rationament
si pentru celelalte fete si insumand rezultatele, se obtine
expresia fluxului total prin paralelipiped, pentru functia 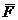 :
:
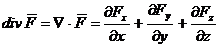 (A.4.13)
(A.4.13)


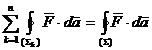 ,
(A.4.7)
,
(A.4.7)