Estimarea formei semnalului (varianta discreta)

Filtru liniar discret(Wiener discret)


 X=
X= n=
n= 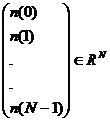
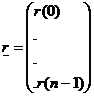
semnal de transmis zgomot semnal receptionat
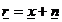 zgomotul
este aditiv(rel. 1)
zgomotul
este aditiv(rel. 1)
 semnalul
estimate (filtrare liniara) (rel. 2)
semnalul
estimate (filtrare liniara) (rel. 2)
matriceaa filtrului: (H)NxN=
filtrarea inseamna eliminarea (pe cat posibil) a zgomotului
 (rel.3) se doreste minimizarea lui
(rel.3) se doreste minimizarea lui
Ipoteze se dau  (rel.4 matricea de covariatie a semnalului unde
(rel.4 matricea de covariatie a semnalului unde 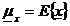 (rel.5).
(rel.5).
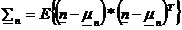 (rel.6) = maatricea de
covariatie a zgomotului, unde
(rel.6) = maatricea de
covariatie a zgomotului, unde  (rel.7).
(rel.7).
Mai presupunem:  (rel.8
(rel.8  (nu afecteaza prea mult generalitatea )
(nu afecteaza prea mult generalitatea ) 
deci rel.4 si rel.6 devin matrici de corelatie:

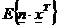 =0 (rel.10) matricea de corelatie mutuala intre semnal
sizgomot e ste nula (se intampla in majoritatea cazurilor)adica x si n
sunt necorelate.
=0 (rel.10) matricea de corelatie mutuala intre semnal
sizgomot e ste nula (se intampla in majoritatea cazurilor)adica x si n
sunt necorelate.
 =
=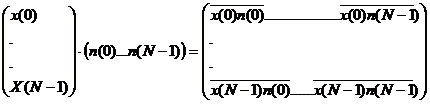
din rel.8,9,1 rezulta 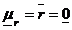
Ipotezele de mai sus sunt de fapt statistica
semnalului si zgomotului, utile la proiectarea filtrului:
Din rel.2 si 3 rezulta 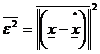 =
=
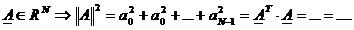
 si
si  (B, A matrici astfel incat sa existe produsul)
(B, A matrici astfel incat sa existe produsul)
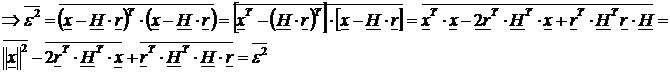
 , iar
, iar  =C ;
=C ; 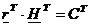
Scoatem H din rel.12 a.i.  sa fie minim. Conditia necesara (nu suficienta) pentru
extremul unei functii.este derivata =0.
sa fie minim. Conditia necesara (nu suficienta) pentru
extremul unei functii.este derivata =0.
Aici nu avem derivata, gradient (care contine
derivate partiale). Aici conditia necesara (care este si suficienta) va dveni: 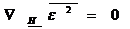
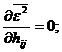
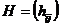 ;
; 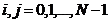 - echivalenta cu N
ecuatii scalare;
- echivalenta cu N
ecuatii scalare;
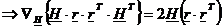 rel.15
rel.15
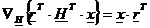 rel.16
rel.16
 rel.17
rel.17
(12)
 ((12)..)=0
((12)..)=0
Se considera (15),(16),(17)
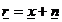
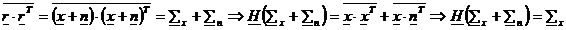 rel.18
rel.18

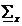 =E
=E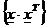
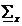 =E
=E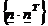

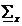 (
(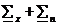 )-1 rel.19 - filtrul obtinut Wiener discret se mai
numeste si filtru Wiener discret vectorial
)-1 rel.19 - filtrul obtinut Wiener discret se mai
numeste si filtru Wiener discret vectorial
Caz particular:
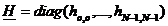 - matricea diagonala
- matricea diagonala  filtrul Wiener discret
scalar
filtrul Wiener discret
scalar
Filtrul Wiener discret scalar:
Scop: reducerea volumului computational (care
la filtrul scalar e foarte mare) adica optimizarea algoritmului.
Filtrul scalar  H =
mat.diagonala
H =
mat.diagonala  N multiplicari, fata
de N2 in cazul filtrului vectorial, in relatia:
N multiplicari, fata
de N2 in cazul filtrului vectorial, in relatia:
 rel.18
rel.18
filtrul va arata astfel:



 x
x 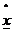


T transformata ortogonala, adica:  rel.20
rel.20
La filtrul vectorial aveam  , aici :
, aici : 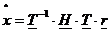 (se deduce din schema
), unde H este pentru filtrul scalar
(se deduce din schema
), unde H este pentru filtrul scalar

 (de acum vom nota Hscalar=H)
(de acum vom nota Hscalar=H)
 in (18) vom avea:
in (18) vom avea:
 ecuatia
filtrului scalar rel.21
ecuatia
filtrului scalar rel.21
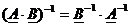
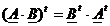
 rel.22
rel.22


 rel.23
rel.23
H0
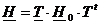 rel.24
rel.24
 rel.25
rel.25
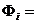 vectorii
propii ai matricei
vectorii
propii ai matricei 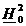
 rel.26 i=0,1,2, . .,N-1
rel.26 i=0,1,2, . .,N-1
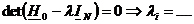
Din (23),(24),(25),(26),(27) 





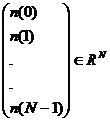
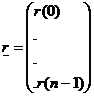



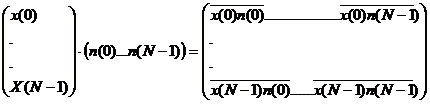
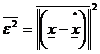 =
= si
si 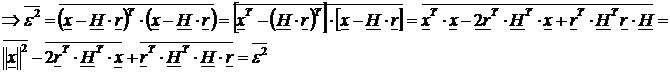
 , iar
, iar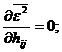



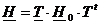 rel.24
rel.24