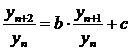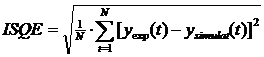1.Obiective
Determinarea modelului unui sistem,
avand la dispozitie raspunsul pondere, prin metoda lui Tapkin .
2.Metodologia de lucru
Modelul se identifica plecand de la raspunsul sistemului la semnal de
intrare de tip impuls prin determinarea parametrilor conform metodei din [1].
Metoda presupune aproximarea sistemului printr-un model de ordinul II de
forma:
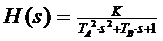
(1)
Din raspunsul pondere se determina valorile parametrilor TA si TB,
avand rolul unor constante de timp. Valoarea amplificarii statice, K, va fi
determinata prin aplicarea unui semnal
de intrare de tip treapta sistemului.
3.Identificarea modelului
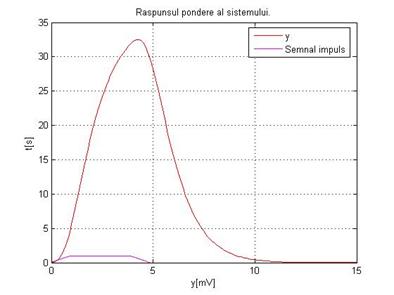
Raspunsul sistemului al carui model se identifica este prezentat in Figura
1.
Figura 1. Raspunsul
pondere al sistemului
Metoda
de identificare presupune prelucrarea sirului valorilor masurate din momentul
incetarii excitatiei de tip impuls. Din acest sir de valori se va aproxima o
dreapta provenita din perechile de valori date de rapoartele: yn+1/yn
si yn+2/yn avand forma:
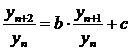
(2)
unde:
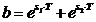
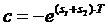
(4)
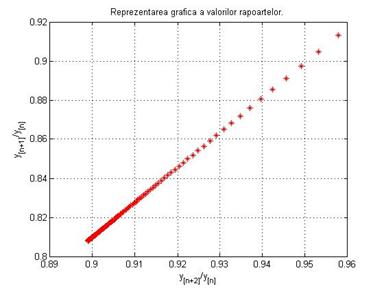
Perechile de valori date de rapoartele yn+1/yn
si yn+2/yn sunt reprezentate in Figura2.
Figura 2. Reprezentarea grafica a valorilor
rapoartelor yn+1/yn si yn+2/yn
Curba care trebuie reprezentata se
obtine din date experimentale prin dreapta de regresie, care are ecuatia :
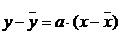
unde parametrul a
se determina cu relatia:
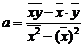
(6)
, unde :
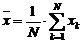
(7)
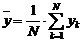
(8)
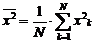
(9)
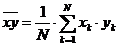
(10)
Parametrul K este determinat prin aplicarea
la intrarea sistemului a unui semnal de tip treapta cu ajutorul formulei:
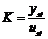
(11)
2
Valorile luate de parametrii modelului sunt concentrate in Tabel 1.
|
Parametru
|
Valoare
|
Parametru
|
Valoare
|
Parametru
|
Valoare
|
Coeficientul unghiular
(b)
|
|
Distanta de la Ox la ec(5)∩Oy
(c)
|
|
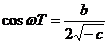
|
|
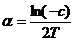
|
|
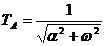
|
|
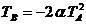
|
|
| | | | | | |
Tabel 1. Parametrii modelului determinat prin metoda lui Tapkin
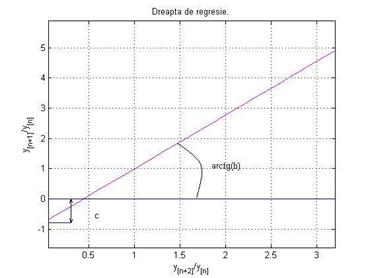
In Figura 3 este reprezentata dreapta de regresie dupa ce au fost
determinati parametrii b si c.
Figura 3.
Reprezentarea grafica a dreptei de regresie
Datorita faptului ca 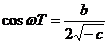 =1 unde T=0.1 rezulta ca =0. Din aceasta constatare se poate spune ca polii
modelului de ordinul II sunt reali.
=1 unde T=0.1 rezulta ca =0. Din aceasta constatare se poate spune ca polii
modelului de ordinul II sunt reali.
Prin inlocuirea
parametrilor K, TA si TB in ecuatia (1)
rezulta:
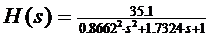
(12)
unde polii sistemului sunt:
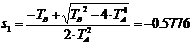
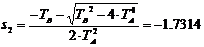
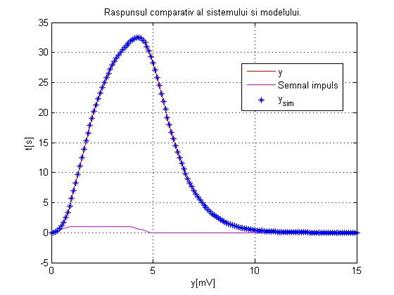
Figura 4.
Reprezentarea grafica raspunsului sistemului si modelului la intrare impuls
Utilizand eroarea medie patratica drept indicator de calitate se obtine:
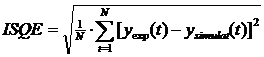
(13)
ISQE=0.020 (14)
4.Concluzii
Metoda de determinare a modelului unui sistem prin metoda lui Tapkin este o metoda care necesita un efort
mai mare din partea utilizatorului. Acesta trebuie sa traseze curba necesara
determinarii parametrilor printr-o metoda de regresie si sa obtina valorile
parametrilor.
Cu aceasta metoda se pot determina
parametrii unui model de ordin II, model suficient de complex pentru o aproximare de ordin superior.
Factorul de calitate obtinut prin
metoda lui Tapkin este net
superior fata de cel al metodelor de determinare a parametrilor din raspunsul
indicial si pondere.
6.Bibliografie
[1] Isoc, D. (2001), Practica
modelarii matematice asistate de calculator a dinamicii sistemelor, Mediamira,
Cluj-Napoca