NOTIUNI TERMODINAMICE DE BAZA.
LEGILE GAZULUI IDEAL. PRINCIPIILE TERMODINAMICII
Notiuni, legi si formule. Indicatii
metodice
Prin fenomen
termic se intelege orice fenomen fizic legat de miscarea
termica a particulelor (atomi, molecule, ioni).
Termodinamica studiaza fenomenele termice
fara a tine seama de structura interna a corpurilor.
Orice corp
macroscopic sau ansamblu de corpuri macroscopice formeaza un sistem
termodinamic (S.T.).
Corpurile care nu fac parte din sistem se numesc
corpuri exterioare sau mediu exterior.
Sistemul termodinamic este izolat, daca nu
interactioneaza si nu schimba substanta cu mediul
exterior.
Sistemul termodinamic este inchis, daca nu
schimba substanta cu mediul exterior, dar schimba energie.
In termodinamica se studiaza
interactiunea dintre sistem si mediul exterior.
.
Totalitatea proprietatilor sistemului termodinamic la un moment dat
reprezinta starea sistemului.
Parametrii de stare reprezinta ansamblul marimilor fizice masurabile ce
caracterizeaza in mod unic starea sistemului termodinamic.
Exemple de parametri de stare: temperatura,
densitatea, capacitatea calorica, volumul, presiunea etc.
Parametrii de stare pot fi:
a) independenti
- pot lua valori arbitrare;
b) dependenti
- pot fi exprimati in functie de
parametrii independenti cu ajutorul unor relatii matematice.
Starea unui sistem termodinamic se
numeste stare stationara, daca toti parametrii
de stare ce o caracterizeaza nu variaza in timp.Starea
stationara se numeste stare de echilibru termodinamic, daca
ea nu se datoreaza unor fenomene care au loc in mediul exterior.
De exemplu, unul din capetele unei tije metalice este
introdus intr-un amestec de apa si gheata, aflat la
presiune atmosferica normala (la temperatura de 0°C), iar
celalalt capat este introdus in apa in fierbere. in acest caz,
temperaturile celor doua capete nu se modifica in timp, dar starea
stationara a tijei nu este o stare de echilibru termodinamic,
deoarece pentru mentinerea constanta a temperaturilor de la capetele
tijei, tija primeste energie sub forma de caldura de la apa
aflata in fierbere si cedeaza energie amestecului de apa
si gheata sub forma de caldura.
Termodinamica studiaza in principal sisteme
termodinamice aflate in stare stationara, precum si
transformarile intre astfel de stari.
Daca parametrii de stare se modifica in timp, atunci starea
sistemului termodinamic este nestationara.
Starea de echilibru termodinamic a
sistemului este determinata de catre parametrii principali de
stare.
Pentru un sistem chimic omogen, parametrii de stare principali sunt: volumul
specific (vs), presiunea (p) si temperatura (T). Volumul specific reprezinta volumul
unitatii de masa.
In starea de echilibru termodinamic:
a) parametrii
de stare ai sistemului termodinamic sunt egali cu parametrii de stare
corespunzatori ai mediului exterior;
b) parametrii
de stare p, vs si T iau aceleasi valori in tot
sistemul termodinamic.
intre cei trei parametri de stare principali exista o relatie
matematica de
legatura, numita ecuatie termica de stare: p= f(v,,T).
Trecerea sistemului dintr-o stare in alta
se numeste proces sau
transformare de stare.
Daca parametrii de stare variaza in timp
atat de lent, incat in orice moment sistemul poate fi considerat in echilibru,
atunci transformarea se numeste cvasistatica.
Transformarile cvasistatice pot fi reprezentate
grafic.
Transformarea in urma careia sistemul
termodinamic trece dintr-o stare initiala de echilibru intr-o stare
finala de echilibru, fara a trece succesiv prin stari
intermediare de echilibru, se numeste transformare necvasistatica.
Transformarile necvasistatice nu pot fi
reprezentate grafic, deoarece in
acest caz nu se mai poate vorbi despre parametri principali de stare (p, vs,
T), care iau aceleasi valori in orice punct al sistemului
termodinamic.
Daca starea finala a sistemului termodinamic
coincide cu starea initiala, atunci transformarea se
numeste ciclica.
O transformare in care in urma
schimbarii semnului de variatie a parametrilor de stare, sistemul
termodinamic evolueaza de la starea finala spre starea
initiala trecand prin aceleasi stari intermediare de
echilibru prin care a trecut in transformarea de la starea initiala
la cea finala, se numeste transformare reversibila.
O transformare care nu este reversibila se
numeste ireversibila. Transformarile necvasistatice sunt
ireversibile. Procesele din
natura sunt ireversibile, adica se desfasoara intr-un
anumit sens si nu se pot desfasura de la sine in sens
opus.
Lucrul mecanic in termodinamica
in procesul de interactiune a sistemului termodinamic cu mediul
exterior, fortele exterioare provoaca actiuni mecanice in
urma carora:
a) starea
sistemului termodinamic nu se modifica, realizandu-se numai o deplasare
mecanica a intregului sistem;
b) sistemul
termodinamic paraseste starea de echilibru termodinamic, efectuand
o transformare in care unii parametrii de stare variaza in timp.
in termodinamica se ia in considerare numai lucrul mecanic schimbat de
sistemul termodinamic cu mediul exterior intr-o transformare.
Parametrii de pozitie sunt
parametri de stare care depind de dimensiunile sistemului si a
caror variatii in timp arata ca sistemul paraseste
starea de echilibru in urma schimbului de lucru mecanic cu exteriorul, permitand
evaluarea lucrului mecanic daca se cunosc fortele interne. □
La fluide exista un singur parametru de pozitie, volumul.
Prin conventie, lucrul
mecanic efectuat de sistemul termodinamic asupra mediului exterior se
considera pozitiv si lucrul mecanic efectuat de mediul
exterior asupra sistemului termodinamic se considera negativ. Cu
aceasta conventie, lucrul mecanic se defineste in
termodinamica cu relatia:
L = pe-AV
unde pe = ct. reprezinta presiunea exterioara,
iar AV reprezinta variatia
volumului sistemului termodinamic. In cazul in care presiunea
exterioara nu este constanta (pe = ct.), se
defineste lucrul mecanic elementar pentru o variatie foarte
mica a volumului (dV) sistemului termodinamic, in care
variatia presiunii exterioare poate fi neglijata.
in acest caz: δL = pedV .
Caldura
reprezinta o forma a schimbului
de energie in care se realizeaza schimbul direct de energie intre
particulele care se misca haotic, ale corpurilor aflate in
interactiune. in acest caz, se intensifica miscarea
dezordonata a particulelor, deci creste energia interna.
Procesul de transfer al energiei interne, fara efectuare de lucru
mecanic, se numeste schimb de caldura. in procesul de
schimb de caldura nu are loc transformarea unei forme de energie in
alta: in acest proces, o parte din energia interna a unui corp se
transfera altui corp, sau unor parti ale aceluiasi corp.
Caldura (Q) reprezinta energia
transmisa sistemului termodinamic in urma schimbului de caldura.
Ca relatie matematica de definitie a caldurii se
foloseste expresia matematica a principiului I al termodinamicii:
Q = L + AU. Tinand cont de
conventia de semn adoptata pentru lucrul mecanic in
termodinamica, rezulta ca daca sistemul primeste
energie in urma schimbului de caldura, atunci Q > 0 J, iar
daca sistemul cedeaza energie in urma schimbului de
caldura, atunci Q < 0 J .
□in majoritatea manualelor de fizica de
liceu sau gimnaziu si chiar in unele lucrari de specialitate, se
afirma ca sistemul primeste caldura daca
el primeste energie in urma schimbului de caldura cu mediul
exterior si ca sistemul cedeaza caldura daca
el cedeaza energie in urma schimbului de caldura cu mediul
exterior.
O transformare in care sistemul termodinamic nu
schimba energie sub forma de caldura cu exteriorul (Q =
0 J) se numeste transformare adiabática.
Energia
totala a sistemului termodinamic (W) este
egala cu suma dintre:
a) energia cinetica a miscarii
macroscopice ca un intreg a sistemului termodinamic (Zsc.);
b) energia potentiala datorata
campurilor conservative de forte externe I^O*'-) j. s2 exemplu: campul electric, campul
gravitational, campul fortelor
elastice;
c) energia
interna (U).
Deci, W = EC+Epext+U. Energia
interna (U) a sistemului termodinamic este energia care depinde numai
de starea termodinamica a sistemului, de caracterul miscarii
si
interactiunii particulelor din sistem. Ea se compune din:
. energia cinetica a particulelor sistemului,
datorata miscarii termice;
. energia potentiala de interactiune a
particulelor, datorata fortelor intermoleculare;
. energia potentiala in campul fortelor
externe a tuturor particulelor din sistem, daca se modifica starea de
echilibru a sistemului;
. energia electronilor din invelisurile
electronice ale atomilor, moleculelor sau ionilor;
. energia nucleului.
□ in majoritatea proceselor termodinamice,
ultimele doua forme de energie raman constante, deoarece nu se
modifica structura particulelor din sistem. Din aceasta cauza,
ele nu se iau in discutie, iar in manualul de fizica de liceu nici nu
sunt introduse in definitia energiei interne a sistemului termodinamic.
□ Energia interna este o marime de
stare, adica variatia energiei interne la trecerea dintr-o stare
de echilibru in alta, nu depinde de starile intermediare prin care trece
sistemul si de caracterul reversibil sau ireversibil al
transformarii, ci doar de cele doua stari.
□ Energia interna este o marime
aditiva, adica energia interna a sistemului termodinamic
este egala cu suma energiilor interne ale partilor componente
ale sistemului.
□ in termodinamica prezinta interes
practic numai variatia energiei interne (AU) si nu energia
interna. Din aceasta cauza, alegerea starii cu energia
interna egala cu zero nu are importanta.
Doua
sisteme termodinamice A si B se afla in contact
termic, daca sistemul (A + B) nu schimba cu exteriorul
energie sub forma de caldura sau sub forma de lucru
mecanic, iar intre sistemele A si B exista schimb de
energie numai sub forma de caldura (nu si sub forma de
lucru mecanic).
Doua sisteme termodinamice aflate in contact termic sunt in echilibru
termic, daca nu schimba intre ele energie sub forma de
caldura.Principiul echilibrului termic. Dupa un interval
de timp mai lung sau mai scurt, sistemul termodinamic atinge o stare de
echilibru termodinamic (termic).
Principiul tranzitivitatii echilibrului
termic. Daca sistemele termodinamice A si
B sunt in echilibru termic, iar sistemul termodinamic B este in
echilibru termic cu sistemul termodinamic C, atunci sistemul A este in
echilibru termic cu sistemul C.
Temperatura empirica este un parametru de stare, care impreuna cu parametrii de
pozitie determina complet starea de echilibru termic a
sistemului.
In termodinamica, temperatura este o
marime fizica ce caracterizeaza sensul schimbului de
caldura intre corpuri. In starea de echilibru termodinamic,
temperatura tuturor corpurilor din sistemul termodinamic discutat este
aceiasi.
Termostatul este
un sistem termodinamic a carui temperatura nu variaza in urma
contactului termic cu alt sistem termodinamic. Pentru ca un sistem termodinamic
sa fie termostat, trebuie ca masa si energia lui sa fie foarte
mari in comparatie cu masa si energia sistemului termodinamic cu care
se afla in contact termic.
Pentru masurarea temperaturii se foloseste
faptul ca la variatia temperaturii corpurile isi
modifica aproape toate proprietatile fizice: lungime si
volum, densitate, conductibilitate electrica etc. Ca baza pentru
masurarea temperaturii poate fi luata variatia oricarei
proprietati fizice a corpului termometrie (lichid, gaz,
rezistor etc), daca pentru ea se cunoaste dependenta
proprietatii fizice respective de temperatura (marimea
fizica respectiva se numeste marime termometrica). Pentru
masurarea temperaturii, termometrul este adus in contact termic cu corpul
a carui temperatura se masoara.
Temperatura masurata cu ajutorul unui
termometru avand scara stabilita cu ajutorul a doua temperaturi de
reper {puncte termometrice) se numeste temperatura
empirica.
Scara de temperatura folosita cel mai mult este scara Celsius,
la care cele doua temperaturi de reper sunt:
. temperatura corespunzatoare starii de
echilibru dintre apa pura si gheata care se topeste la
presiunea atmosferica normala, care in mod conventional se ia
egala cu 0;
. temperatura corespunzatoare starii de
fierbere a apei pure la presiunea atmosferica normala, care in mod
conventional se ia egala cu 100.
Gradul Celsius (°C) se obtine impartind
intervalul de pe scala termometrului, cuprins intre reperele 0 si 100, in
o suta de parti egale.
In Sistemul International de unitati de
masura marimea fizica fundamentala este temperatura
absoluta (7), iar unitatea de masura a temperaturii
absolute este Kelvinul (K).
Legatura dintre temperatura absoluta (T)
si temperatura in scara Celsius
este data de relatia: T(K) = 273,15 + t (°C).
13. Legile
gazului ideal
Legea
Boyle-Mariotte sau legea
transformarii izoterme (v = ct; r= ct):
"intr-o transformare izoterma, presiunea unui gaz ideal variaza
invers proportional cu volumul ocupat de el: p V = ct.'
□ in
sistemul de coordonate (p, V) este o hiperbola echilaterala .
Hiperbola echilaterala este simetrica fata de prima
bisectoare a sistemului de coordonate discutat.
Legea
Gay-Lussac sau legea transformarii izobare (v
= ct.; p = ct.):
a) "intr-o transformare izobara
variatia relativa a volumului unui gaz ideal
este direct proportionala cu temperatura lui: = . t, (1.11), unde:
= . t, (1.11), unde:
. Vq este volumul
ocupat de gaz la temperatura de 0° C;
. V este volumul gazului la temperatura de / (°C);
t este temperatura gazului exprimata in °C;
α este coeficientul de dilatare
izobara.
Coeficientul de dilatare izobara (α) este numeric egal cu variatia
relativa a volumului gazului ideal, atunci cand temperatura lui
variaza cu un grad.
Coeficientul de dilatare termica izobara are
aceeasi valoare pentru toate
gazele si este egal cu α = 
b) "intr-o
transformare izobara volumul gazului ideal creste liniar cu
temperatura: V(t) = V0(1+αt)"
c) "intr-o
transformare izobara, raportul dintre volumul gazului ideal si
temperatura absoluta a lui este constant: 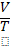 = ct"
= ct"
Figura 1
□ Daca dreptele 1 si 2 reprezinta
transformarea izobara pentru aceeasi masa din acelasi gaz
ideal, atunci p> p2.
Legea
lui Charles sau legea transformarii izocore (v = ct; V= ct.):
a) "intr-o
transformare izocora, variatia relativa a presiunii unui gaz
ideal este direct proportionala cu temperatura lui."
Coeficientul termic al
presiunii este numeric
egal cu variatia relativa a presiunii gazului, atunci cand
temperatura lui variaza cu un grad.
Coeficientul termic al presiunii are aceeasi
valoare pentru toate gazele si
este egal cu β=
b) Intr-o transformare
izocora, presiunea unui gaz ideal creste liniar cu
temperatura lui.
c) intr-o
transformare izocora, raportul dmtre presronea gazulm ideal si
temperatura absoluta a lui este constanta: 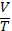 - ct.
- ct.
in figura 2 sunt date cateva reprezentari grafice ale
transformarii izocore in diferite coordonate.

Figura
2
□ Daca dreptele 1 si 2 reprezinta
transformarea izocora pentru aceeasi masa din acelasi gaz
ideal, atunci Vi>V2.
Ecuatia
Clapeyron-Mendeleev sau ecuatia
termica de stare stabileste o dependenta intre
parametrii principali de stare ai gazului ideal,
aflat intr-o stare de echilibru: pV =  RT ,unde:
RT ,unde:
. m este masa gazului ideal (kg);
. μ este masa molara a gazului (kg/mol);
. R este constanta universala a gazelor
si are valoarea egala cu R = = 8,31 J/(mol-K).
Daca m = ct., atunci ecuatia devine: = ct.Din ecuatia Clapeyron-Mendeleev rezulta
dependenta densitatii gazului ideal de temperatura: p(T)
=
= ct.Din ecuatia Clapeyron-Mendeleev rezulta
dependenta densitatii gazului ideal de temperatura: p(T)
=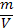 => p(T)
=> p(T) 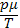 = ct , sau dependenta densitatiigazului de densitatea lui in conditii normale de presiune si
temperatura.
= ct , sau dependenta densitatiigazului de densitatea lui in conditii normale de presiune si
temperatura.
□ Gazul ideal se defineste ca fiind un gaz
care verifica riguros legile Boyle-Mariotte, Gay-Lussac si
Charles, in orice conditii de temperatura si presiune. Gazele
reale (aerul, azotul, oxigenul, hidrogenul, heliul etc.) se
supun legilor de mai sus atunci cand se afla la temperaturi cu mult mai
mari decat temperatura de lichefiere a lor si la presiuni apropiate ca
valoare de presiunea atmosferica.
Ecuatia
calorica de stare da
dependenta energiei interne a sistemului termodinamic de temperatura
si de parametrii de pozitie:
U = U(t,aua2,,an). in cazul gazelor: U == U(t, V). (1.19) in
conformitate cu experienta lui Joule energia
interna a unui gaz ideal depinde numai de temperatura gazului: U=U(T).
(1.20)
Principiul I
al termodinamicii
Principiul intai al termodinamicii reprezinta legea de conservare
si transformare a energiei sistemului, aplicata fenomenelor termice.
Enuntul 1: "in orice transformare, variatia energiei interne (ΔU) a
unui sistem termodinamic, aflat in repaus mecanic, depinde numai de
starile initiala si finala ale sistemului, fiind
independenta de starile intermediare prin
care trece sistemul termodinamic: ΔU=Q-L.
Enuntul 2: "Caldura primita de un sistem termodinamic este egala cu
suma dintre variatia energiei interne a sistemului si lucrul mecanic efectuat de sistem: Q = L + ΔU .
16. Marimile
fizice, care stabilesc o legatura cantitativa intre caldura
(Q) primita sau cedata de un corp si variatia
temperaturii sale (ΔT), se numesc coeficienti calorici. Coeficientii
calorici depind de natura corpului si de conditiile fizice in care
are loc schimbul de caldura.
Capacitatea calorica (C) se defineste ca raportul dintre caldura
primita sau cedata de un corp (Q) si variatia
corespunzatoare a temperaturii lui (ΔT), atunci cand ΔT
-> 0 K:
C=  . Unitatea de
masura a capacitatii calorice este [C]SI =
J/K .
. Unitatea de
masura a capacitatii calorice este [C]SI =
J/K .
Capacitatea calorica este o caracteristica a
corpului si nu a substantei din care este alcatuit.
Caldura specifica (c) se defineste ca raportul dintre caldura (Q)
primita sau cedata de un corp si produsul dintre masa
corpului (m) si variatia corespunzatoare a temperaturii
lui (ΔT).
17. Calculul lucrului mecanic, caldurii
si variatiei energiei interne in transformarile simple
a) intr-o transformare
izoterma lucrul mecanic, caldura si variatia energiei interne se calculeaza
cu formulele: L = vRTln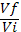
b) intr-o transformare
izocora lucrul mecanic, caldura si variatia energiei
interne se calculeaza cu formulele:
Lv =0J; Qv =v-CvΔT sau Qv =mcvΔT;
AU = Qy.
c) intr-o transformare
izobara lucrul mecanic, caldura si variatia energiei
interne se calculeaza cu formulele:
Lp = pΔV sau Lp
=vRΔT; ΔU = vCv-ΔT sau ΔU = mcvΔT;
Qp=vCpΔT sau Qp=mcpΔT.
d) intr-o transformare adiabática caldura,
variatia energiei interne si lucrul mecanic se calculeaza cu
formulele:
g = 0J; ΔU=vCyΔT sau ΔU = mcv ΔT;
L = -ΔU . Ecuatia transformarii
adiabatice cvasistatice se numeste ecuatia Poisson si
are forma p V = ct.,
□ Deoarece la gaze Cp > Cv, rezulta
ca exponentul adiabatic este supraunitar (γ > 1) si in
coordonate Clapeyron graficul adiabatei este mai inclinat decat graficul izotermei.
Calorimetría se ocupa cu masurarea caldurii si a
caldurii specifice.
in cazul in care mai multe corpuri se afla intr-un sistem Izolat, energia
interna totala a sistemului se conserva. Daca in acest
sistem nu se efectueaza lucru mecanic, atunci in conformitate cu
principiul intai al termodinamicii variatia energiei interne a
fiecarui corp este egala cu caldura primita sau cedata
de corpul respectiv pana la stabilirea echilibrului termodinamic (ΔUi=Qi).
Principiul
al doilea al termodinamicii
Formularea lui Thomson: "intr-o
transformare ciclica monoterma sistemul nu poate efectua lucru
mecanic. Daca transformarea ciclica monoterma este si
ireversibila, atunci sistemul primeste lucru mecanic din
exterior.'
Ciclul
Carnot este o transformare ciclica
biterma, reversibila, formata din doua izoterme si
doua p adiabate (vezi figura 3).

Teoremele lui Carnot:
T.l. Randamentul
unei masini termice care functioneaza dupa un ciclu Carnot
depinde numai de temperaturile celor doua termostate si nu depinde de
constructia masinii si de substanta de lucru folosita.
T.2. Randamentul
unei masini termice care functioneaza dupa un ciclu
ireversibil intre doua termostate de temperaturi date este mai mic decat
randamentul unei masini ideale care ar functiona dupa un ciclu
Carnot reversibil intre aceleasi termostate.
Teorema lui Clausius:
"Intr-un ciclu oarecare, suma caldurilor reduse
nu depinde de forma ciclului si este mai mica sau egala cu zero: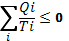
Semnul egal corespunde cazului in care ciclul este
reversibil, iar semnul mai mic corespunde unui ciclu ireversibil. Relatia de
mai sus este cunoscuta sub denumirea de inegalitatea lui Clausius.
Cu ajutorul
inegalitatii lui Clausius, aplicata proceselor reversibile, se
poate defini entropia. Entropia este o functie de stare,
determinata cu o precizie pana la o constanta. Valoarea
acestei constante nu are importanta, deoarece in termodinamica
are semnificatie fizica numai variatia entropiei.
Variatia entropiei sistemului intre doua stari de echilibru 1 si 2 se
defineste ca fiind egala cu caldura redusa pe care trebuie sa
o primeasca sistemul pentru a trece din starea 1 in starea 2 in orice
proces cvasistatic
Legea cresterii entropiei: "Entropia unui sistem termodinamic izolat adiabatic nu
poate sa scada; ea creste sau ramane constanta.'
Entropia unui sistem termodinamic este o marime aditiva.
Aplicatii:
Problema
1. Un gaz ideal sufera o transformare 1
-» 2, care este reprezentata in figura. in care din cele doua
stari (1 sau 2) volumul ocupat de gaz este mai mare? Se vor discuta cazurile
in care p0 > 0Pa, respectiv p0 < 0 Pa
. Masa gazului ideal se pastreaza constanta in acest proces.
Solutie:
Metoda 1. Problema poate fi rezolvata cel mai simplu
grafic. Daca prelungirea segmentului de dreapta ce descrie procesul 1
> 2 ar trece prin origine, atunci
procesul suferit de gaz ar fi izocor si volumul ocupat de gaz ar
ramane constant.
In cazul acestei probleme prelungirea segmentului de
dreapta 1 - 2 nu trece prin origine si, din aceasta cauza,
volumul gazului variaza. Pentru a raspunde la intrebarea pusa in
enunt, ducem prin punctele 1 si 2 doua drepte care trec prin
origine . Aceste drepte reprezinta doua izocore ale aceleiasi
mase de gaz, aflata la volumele Vx = ct., respectiv V2
= ct.
in coordonate (p, T) pantele acestor doua
drepte sunt egale cu 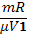 , respectiv cu
, respectiv cu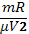 Din figura
1.10 se observa ca daca p0>0Pa (figura1.10a),
atunci panta dreptei Vl=ct este mai mare decat panta dreptei V2
= ct. si, din aceasta cauza Vx < V2
. in cazul in care p0 <0Pa (vezi figura 1.10b), se
observa ca panta dreptei Vx =ct. este mai mica
decat a dreptei V2 = ct. si din aceasta cauza VX>V2.
Din figura
1.10 se observa ca daca p0>0Pa (figura1.10a),
atunci panta dreptei Vl=ct este mai mare decat panta dreptei V2
= ct. si, din aceasta cauza Vx < V2
. in cazul in care p0 <0Pa (vezi figura 1.10b), se
observa ca panta dreptei Vx =ct. este mai mica
decat a dreptei V2 = ct. si din aceasta cauza VX>V2.
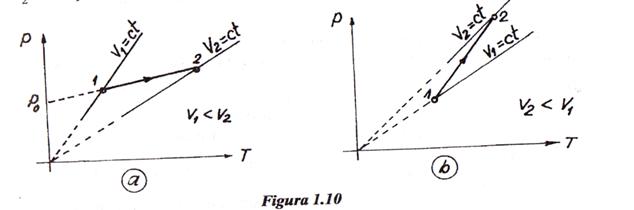
Metoda 2. Problema poate fi rezolvata si analitic. Pentru aceasta scriem
ecuatia dreptei care trece prin punctele 1 si 2: p(T)=a-T + b
Deoarece masa gazului nu variaza in acest proces,
din ecuatiile termice de stare ale gazului ideal scrise pentru cele
doua stari rezulta:

Problema 2.
Intr-un tub sub forma de U, inchis la unul
din capete, se afla mercur. Lungimea coloanei de aer din tubul inchis este
egala cu 2L, iar nivelul mercurului in ramura deschisa este cu
L mai sus fata de nivelul mercurului din ramura inchisa.
Tubul se afla intr-o racheta care incepe sa urce vertical cu
acceleratia g. Sa se calculeze diferenta dintre nivelele
mercurului in cele doua ramuri, daca in interiorul rachetei se
mentine presiunea iitmosferica normala.
Solutie
Deoarece tubul cu lichid urca vertical cu
acceleratia a = g , presiunea hidrostatica exercitata de
o coloana de lichid de inaltime h este egala cu p
= p(g + a)h (vezi capitolul Mecanica fluidelor din lucrarea Metode
de rezolvare a problemelor de fizica, volumul I, Mecanica).
Inainte de pornirea rachetei, aerul din ramura
inchisa a tubului este comprimat si presiunea lui este egala cu
suma dintre presiunea atmosferica si presiunea hidrostatica a
coloanei de mercur de lungime L: pl = pa + p . g
. L .
 In momentul in care racheta incepe sa urce
vertical cu acceleratia a = g, presiunea hidrostatica a
coloanei de mercur de lungime L creste si aerul din ramura inchisa
se comprima. Denivelarea mercurului din cele doua ramuri se
micsoreaza pana cand se stabileste un nou echilibru (vezi
figura 1.22a).
In momentul in care racheta incepe sa urce
vertical cu acceleratia a = g, presiunea hidrostatica a
coloanei de mercur de lungime L creste si aerul din ramura inchisa
se comprima. Denivelarea mercurului din cele doua ramuri se
micsoreaza pana cand se stabileste un nou echilibru (vezi
figura 1.22a).
Figura 1.22a corespunde situatiei in care racheta
se afla in repaus, iar figura 1.22b corespunde situatiei in care racheta
urca cu acceleratia a = g .
Aerul aflat in ramura inchisa sufera o transformare
izoterma, deoarece masa aerului si temperatura lui raman
constante. Conform legii Boyle-Mariotte:
p1 S 2L=S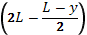
p2=pa+p(g + a)y. (1.13.2)
avand in vedere ca P2 = Pa + ρ · g · L , se obtine:
(pa+ ρ·
g·L)2L = [pa+ ρ (g + a)y](2L- 
Deoarece pa = p-g-H0 (unde H0 = 76cm)
si a = g , ecuatia devine: 4 (H0+L)L = 3L H0
+2y2 +6Ly =>2y2 +6LyL(H0+4L) = 0 .
Solutiile ecuatiei sunt yl2 =
Din aceste doua solutii
are semnificatie fizica numai solutia cu semnul plus in
fata radicalului.