Oscilatorul
amortizat si intretinut
Studiul acestor
oscilatii este deosebit de important din punct de vedere tehnic deoarece
majoritatea oscilatiilor prezente la diferite utilaje in functiune
sunt oscilalatii amortizate si intretinute.
Forta perturbatoare
care intretine oscilatia poate sa fie de natura
diferita.
Prezinta interes: - fortele perturbatoare de forma
sinusoidala;
fortele perturbatoare
generate de masa excentrica in miscare de rotatie.
1 Oscilatii amortizate si intretinute de
forta perturbatoare sinusoidala
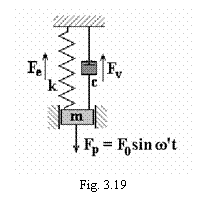
Modelul mecanic al unui astfel de
oscilator este prezentat in figura 3.19.
Ecuatia diferentiala a
miscarii este:
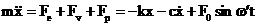 (3.4.54)
(3.4.54)
sau: 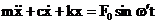 (3.4.55)
(3.4.55)
Impartind
aceasta expresie cu m se obtine ecuatia diferentiala
neomogena de ordinul doi:
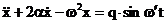 (3.4.56)
(3.4.56)
in care s-a notat:
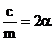 factorul de
amortizare;
factorul de
amortizare;
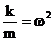 patratul
pulsatiei proprii de oscilatie;
patratul
pulsatiei proprii de oscilatie;
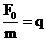 acceleratia
corpului sub actiunea fortei constante F0.
acceleratia
corpului sub actiunea fortei constante F0.
 Solutia ecuatiei diferentiale, sau ecuatia
de miscare este egala cu solutia x1 a ecuatiei
omogene (3.4.16), plus o solutie
particulara x2 a ecuatiei diferentiale (3.4.56), de
forma termenului liber (perturbator): x
= x1 + x2
Solutia ecuatiei diferentiale, sau ecuatia
de miscare este egala cu solutia x1 a ecuatiei
omogene (3.4.16), plus o solutie
particulara x2 a ecuatiei diferentiale (3.4.56), de
forma termenului liber (perturbator): x
= x1 + x2
Prima solutie x1
este data de relatia (3.4.23) iar cea de-a doua solutie este de
forma:
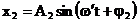 (3.4.57)
(3.4.57)
Deci:
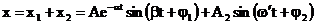 (3.4.58)
(3.4.58)
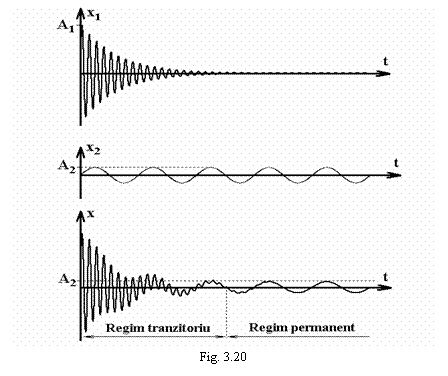 Cele doua oscilatii x1 si x2
precum si oscilatia rezultanta x sunt prezentate grafic in
figura 3.20.
Cele doua oscilatii x1 si x2
precum si oscilatia rezultanta x sunt prezentate grafic in
figura 3.20.
Se observa din
graficul miscarii ca exista doua regimuri de
oscilatie, diferite.
La intervale scurte de
timp de la inceperea oscilatiei, miscarea oscilatorie este
nearmonica. Acest regim de oscilatie se numeste regim
tranzitoriu.
Dupa scurgerea unui
interval de timp destul de lung, deoarece amplitudinea oscilatiei x1 tinde
spre zero, oscilatia rezultanta va fi descrisa de x2.
Acest regim de oscilatie se numeste regim permanent, iar
miscarea oscilatorie a sistemului este armonica, de ecuatie:
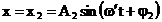 (3.4.59)
(3.4.59)
Deci, in regim permanent,
oscilatia amortizata si intretinuta de o
forta perturbatoare este o oscilatie armonica, de
amplitudine A2 si de faza initiala j . Aceste doua constante se pot
determina inlocuind solutia particulara x2, prima
derivata a acesteia 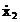 si cea de-a doua derivata
si cea de-a doua derivata 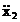 in ecuatia
diferentiala a miscarii (3.4.56). Prin identificarea
termenilor ecuatiei se obtine un sistem de doua ecuatii cu
doua necunoscute A2 si j descrise de relatiile:
in ecuatia
diferentiala a miscarii (3.4.56). Prin identificarea
termenilor ecuatiei se obtine un sistem de doua ecuatii cu
doua necunoscute A2 si j descrise de relatiile:
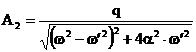 (3.4.60)
(3.4.60)
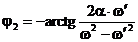 (3.4.61)
(3.4.61)
Aceste doua relatii se pot aduce sub o alta forma
daca se imparte atat numaratorul cat si numitorul cu 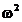 . Se obtine:
. Se obtine:
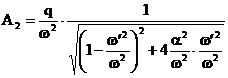 (3.4.62)
(3.4.62)
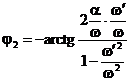 (3.4.63)
(3.4.63)
In aceste relatii se inlocuieste: 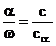 in care c este
coeficientul de amortizare vascoasa iar ccr. este coeficientul
critic de amortizare vascoasa, definit de relatia (3.4.19). Se
obtine:
in care c este
coeficientul de amortizare vascoasa iar ccr. este coeficientul
critic de amortizare vascoasa, definit de relatia (3.4.19). Se
obtine:
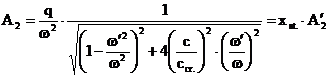 (3.4.64)
(3.4.64)
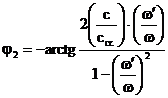 (3.4.65)
(3.4.65)
In aceste relatii xst. este deformarea statica iar
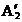 este o marime
adimensionala, numita factor de amplificare, avand expresia:
este o marime
adimensionala, numita factor de amplificare, avand expresia:
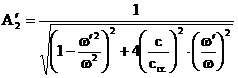 (3.4.66)
(3.4.66)
Deformarea statica xst. mai poate fi scrisa:
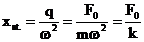 (3.4.67)
(3.4.67)
si reprezinta alungirea elementului elastic de constanta
elastica k sub actiunea fortei constante F0,
egala cu valoarea maxima a fortei perturbatoare sinusoidale.
Deci amplitudinea oscilatorului
amortizat si intretinut este egala cu produsul dintre deformarea
statica xst. si factorul de amplificare 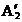 .
.
Se observa ca
atat amplitudinea A2 cat si faza initiala j depind de raportul 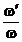 si de raportul
si de raportul 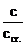 . Graficul ce reprezinta dependenta factorului de
amplificare de raportul
. Graficul ce reprezinta dependenta factorului de
amplificare de raportul 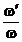 pentru diferite valori
ale raportului
pentru diferite valori
ale raportului 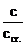 este prezentat in
figura 3.21.
este prezentat in
figura 3.21.
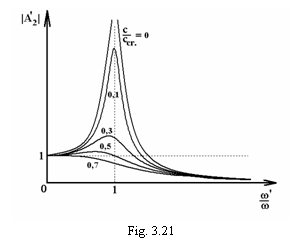 Familia curbelor, numite curbe de rezonanta sau
curbe de raspuns, prezinta maxime ale caror valoare maxima
scade atunci cand creste valoarea raportului
Familia curbelor, numite curbe de rezonanta sau
curbe de raspuns, prezinta maxime ale caror valoare maxima
scade atunci cand creste valoarea raportului 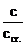 . De asemenea se poate constata ca maximul factorului de
amplificare se produce la valori tot mai mici ale raportului
. De asemenea se poate constata ca maximul factorului de
amplificare se produce la valori tot mai mici ale raportului 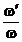 pe masura ce
creste raportul
pe masura ce
creste raportul 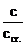 . In lipsa amortizarii, raportul
. In lipsa amortizarii, raportul 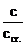 are valoarea zero, obtinandu-se astfel curba de
raspuns, la forta perturbatoare, a oscilatorului neamortizat si
intretinut de forta perturbatoare sinusoidala.
are valoarea zero, obtinandu-se astfel curba de
raspuns, la forta perturbatoare, a oscilatorului neamortizat si
intretinut de forta perturbatoare sinusoidala.
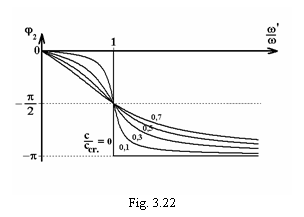 Graficul de variatie a fazei initiale j in functie de raportul
Graficul de variatie a fazei initiale j in functie de raportul 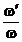 pentru diferite valori
ale raportului
pentru diferite valori
ale raportului 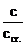 este prezentat in
figura 3.22. Din acest grafic se observa ca in lipsa amortizarii
oscilatia rezultanta este in faza cu forta perturbatoare (j = 0), pentru valori subunitare ale
raportului
este prezentat in
figura 3.22. Din acest grafic se observa ca in lipsa amortizarii
oscilatia rezultanta este in faza cu forta perturbatoare (j = 0), pentru valori subunitare ale
raportului 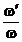 . La valori supraunitare ale raportului
. La valori supraunitare ale raportului 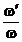 , oscilatia rezultanta este in opozitie de faza
cu forta perturbatoare (j p) . De asemenea se observa ca,
indiferent de valoarea raportului
, oscilatia rezultanta este in opozitie de faza
cu forta perturbatoare (j p) . De asemenea se observa ca,
indiferent de valoarea raportului 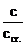 , toate curbele trec prin acelasi punct de abscisa
, toate curbele trec prin acelasi punct de abscisa 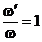 si ordonata
si ordonata 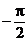 .
.
Pentru a putea afla valoarea
amplitudinii oscilatiei la rezonanta, trebuie determinata
valoarea raportului 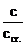 la
rezonanta. Maximul curbei, la rezonanta, pentru un anumit
grad de amortizare, se obtine derivand factorul de amplificare
la
rezonanta. Maximul curbei, la rezonanta, pentru un anumit
grad de amortizare, se obtine derivand factorul de amplificare 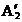 in raport cu
in raport cu 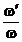 si punand
conditia ca derivata sa fie egala cu zero. Efectuand
aceasta derivata si punand conditia de rezonanta
se obtine:
si punand
conditia ca derivata sa fie egala cu zero. Efectuand
aceasta derivata si punand conditia de rezonanta
se obtine: 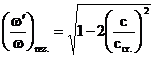 (3.4.68)
(3.4.68)
Inlocuind aceasta valoare in expresia amplitudinii si a fazei
initiale se obtine:
 (3.4.69)
(3.4.69)
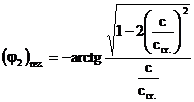 (3.4.70)
(3.4.70)
Din punct de vedere
practic este foarte important sa se cunoasca valoarea amplitudinii
sistemului oscilant, la rezonanta, pentru a putea preveni efectele
nedorite, datorita intrarii sistemului in rezonanta cu
forta perturbatoare. Se cunosc numeroase cazuri cand sisteme oscilante au
fost distruse datorita amplitudinii prea mari a oscilatiei sistemului
cand acesta intra in rezonanta cu forta perturbatoare.
Exista insa,
situatii cand fenomenul de rezonanta este provocat, in scopuri
utile. Aparatele pentru masurarea frecventelor oscilatiilor se
bazeaza tocmai pe fenomenul de rezonanta.
2 Oscilatii amortizate
si intretinute de forta perturbatoare generata de
masa excentrica in rotatie
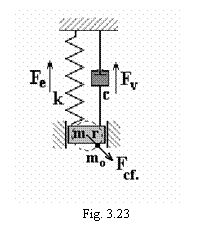 Modelul mecanic al
oscilatorului este prezentat in figura 3.23. Forta perturbatoare este
tocmai componenta verticala a fortei centrifuge ce
actioneaza asupra corpului de masa m0 care se
roteste cu viteza unghiulara w pe o traiectorie circulara de raza r.
Modelul mecanic al
oscilatorului este prezentat in figura 3.23. Forta perturbatoare este
tocmai componenta verticala a fortei centrifuge ce
actioneaza asupra corpului de masa m0 care se
roteste cu viteza unghiulara w pe o traiectorie circulara de raza r.
Studiul acestui oscilator este asemanator cu cel al
oscilatorului amortizat si intretinut de forta
perturbatoare sinusoidala. In acest caz forta perturbatoare este
data de componenta verticala a fortei centrifuge:
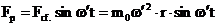 (3.4.71)
(3.4.71)
Rezultatul la care se ajunge este acela ca la cazul prezentat anterior
si anume ca miscarea oscilatorie este armonica (in regim
permanent), de pulsatie identica cu pulsatia fortei
perturbatoare.
Faza initiala a oscilatiei este, de asemenea,
aceeasi cu cea data de relatia (3.4.65), insa amplitudinea
oscilatiei este diferita si are expresia:
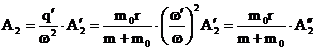 (3.4.72)
(3.4.72)
deoarece: 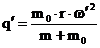 (3.4.73)
(3.4.73)
Factorul de amplificare 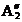 , in cazul oscilatiilor amortizate si
intretinute de forta perturbatoare generata de masa
excentrica in rotatie, are expresia:
, in cazul oscilatiilor amortizate si
intretinute de forta perturbatoare generata de masa
excentrica in rotatie, are expresia:
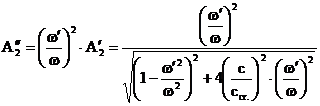 (3.4.74)
(3.4.74)
Dependenta
factorului de amplificare 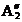 de raportul
de raportul 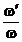 pentru diferite valori
ale raportului
pentru diferite valori
ale raportului 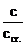 este prezentata
in figura 3.24.
este prezentata
in figura 3.24.
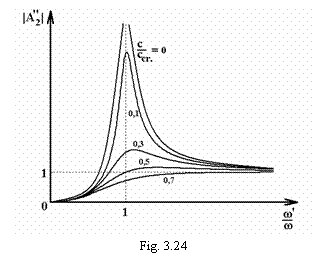 Curbele de rezonanta difera de cele
prezentate in cazul oscilatiilor amortizate si intretinute de
forta perturbatoare sinusoidala.
Curbele de rezonanta difera de cele
prezentate in cazul oscilatiilor amortizate si intretinute de
forta perturbatoare sinusoidala.
Curbele care arata
dependenta fazei initiale de raportul 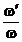 sunt identice cu cele
prezentate in figura 3.22.
sunt identice cu cele
prezentate in figura 3.22.
Studierea, in continuare,
a comportarii sistemului la rezonanta se face
asemanator cu cea de la oscilatorul amortizat si intretinut
de forta perturbatoare sinusoidala.
Si in acest caz apar fenomene
nedorite in tehnica. De exemplu, sa consideram un motor cu o
anumita excentricitate a rotorului. Prin rotatie, rotorul creaza
o forta perturbatoare periodica, ce produce trepidatia
motorului impreuna cu suportul pe care se gaseste. La
rezonanta, motorul transmite suportului energie maxima, iar
amplitudinea oscilatiilor poate atinge valori periculoase. Daca
turatia motorului se modifica, sistemul iese din regimul de rezonanta
si amplitudinea oscilatiilor scade.


 Solutia ecuatiei diferentiale, sau ecuatia
de miscare este egala cu solutia x1 a ecuatiei
omogene (3.4.16), plus o solutie
particulara x2 a ecuatiei diferentiale (3.4.56), de
forma termenului liber (perturbator): x
= x1 + x2
Solutia ecuatiei diferentiale, sau ecuatia
de miscare este egala cu solutia x1 a ecuatiei
omogene (3.4.16), plus o solutie
particulara x2 a ecuatiei diferentiale (3.4.56), de
forma termenului liber (perturbator): x
= x1 + x2 Cele doua oscilatii x1 si x2
precum si oscilatia rezultanta x sunt prezentate grafic in
figura 3.20.
Cele doua oscilatii x1 si x2
precum si oscilatia rezultanta x sunt prezentate grafic in
figura 3.20.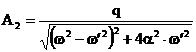 (3.4.60)
(3.4.60)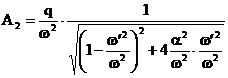 (3.4.62)
(3.4.62)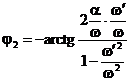 (3.4.63)
(3.4.63)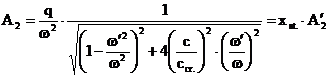 (3.4.64)
(3.4.64)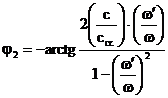 (3.4.65)
(3.4.65)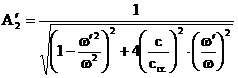 (3.4.66)
(3.4.66) Familia curbelor, numite curbe de rezonanta sau
curbe de raspuns, prezinta maxime ale caror valoare maxima
scade atunci cand creste valoarea raportului
Familia curbelor, numite curbe de rezonanta sau
curbe de raspuns, prezinta maxime ale caror valoare maxima
scade atunci cand creste valoarea raportului  Graficul de variatie a fazei initiale
Graficul de variatie a fazei initiale 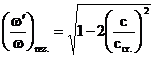 (3.4.68)
(3.4.68) (3.4.69)
(3.4.69)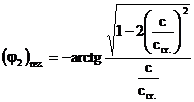 (3.4.70)
(3.4.70)
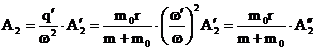 (3.4.72)
(3.4.72)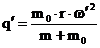 (3.4.73)
(3.4.73)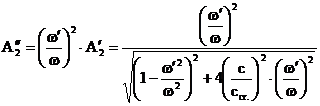 (3.4.74)
(3.4.74) Curbele de rezonanta difera de cele
prezentate in cazul oscilatiilor amortizate si intretinute de
forta perturbatoare sinusoidala.
Curbele de rezonanta difera de cele
prezentate in cazul oscilatiilor amortizate si intretinute de
forta perturbatoare sinusoidala.