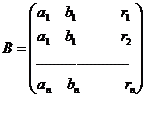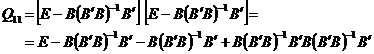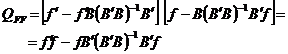Prelucrarea marimilor masurate direct si
supuse la conditii
1 Marimi
masurate direct, supuse la conditii de aceeasi precizie.
1.1 Calculul
valorilor probabile
Pentru aceasta categorie de
masuratori, caracteristic este sistemul de ecuatii a carui
forma este:
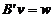
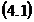
in care:

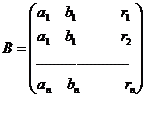
La sistemul de
ecuatii 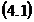 se ataseaza conditia:
se ataseaza conditia:
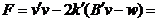 minim
minim
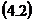
Care conduce la:
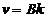
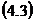
Si:
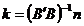
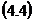
1.2 Calculul
preciziilor
Consta in determinarea
coeficientilor de pondere ai marimilor obtinute prin
masuratori conditionate.
Se porneste de la
egalitatile:
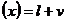
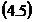
Dar din 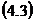 si
si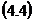
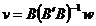
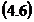
Insa:
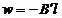
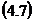
Si atunci:
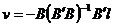
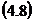
Inlocuind egalitatiile
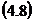 in
in 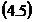 obtinem:
obtinem:
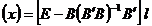
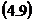
Ecuatia 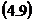 arata
ca valorile probabile ale marimilor masurate direct si
supuse la conditii sunt functii de marimile masurate
direct. In consecinta
se poate aplica formula
arata
ca valorile probabile ale marimilor masurate direct si
supuse la conditii sunt functii de marimile masurate
direct. In consecinta
se poate aplica formula 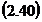 in care ponderile sunt egale cu unitatea
si avem:
in care ponderile sunt egale cu unitatea
si avem:
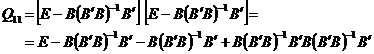

sau
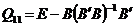
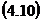
Pentru cazul unei
functii masurate indirect
si de aceeasi precizie, consideram:
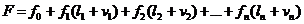
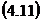
Sau matricial:
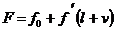
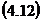
in care:
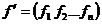 - matricea transpusa a matricei (coloana) a coeficientilor
- matricea transpusa a matricei (coloana) a coeficientilor
din functie.
Luand in considerare
relatia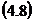 se poate
scrie functia data ca dependenta explicit de marimile
masurate, astfel:
se poate
scrie functia data ca dependenta explicit de marimile
masurate, astfel:
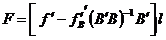

Folosind din nou formula 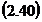 se obtine expresia matriceala a coeficientul
de pondere al functiei. Astfel:
se obtine expresia matriceala a coeficientul
de pondere al functiei. Astfel:
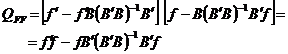

Sau
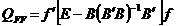
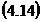
Conform egalitatii 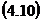 egalitatea
egalitatea 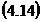 devine:
devine:
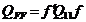
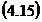
2 Marimi
masurate indirect supuse la conditii si de precizii diferite.
2.1 Calculul
valorilor probabile.
Reluam
sistemului de ecuatii al corectiilor 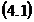 specific masuratorilor
conditionate de aceeasi precizie.
specific masuratorilor
conditionate de aceeasi precizie.
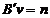
Corectiile
din acest sistem au erori probabile (ponderi) diferite, deci v-a exista o matrice a ponderilor notata astfel:
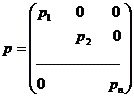
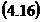
Atasam sistemului ecuatiilor de erori conditia:
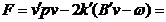 minim
minim 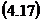
Valorile corectiilor, pentru care indeplinita,
conditia 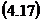 verifica sistemul:
verifica sistemul:

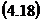
Derivand obtinem:
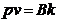
Sau:
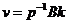
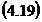
Cu care 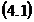 devine:
devine:
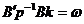
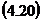
Notam:
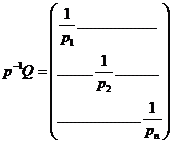
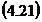
si putem
scrie:
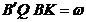 (22)
(22)
de unde:
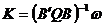 (23)
(23)
Sistemul de ecuatii (22)
reprezinta sistemul de ecuatii normale pentru masuratorile
conditionate de precizii diferite. Ordinea de rezolvare este:
Se calculeaza corelatele cu
egalitatea (23);
Se calculeaza valorile
probabile ale corectiilor cu egalitatea (19).
2.2 Calculul
preciziilor
Consta in determinarea
coeficientilor de pondere ai marimilor determinate si al unei
functii de aceste marimi.
Pentru calculul coeficientilor
de pondere ai corectiilor si in consecinta ai
marimilor determinate vom scrie:
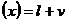
Dar:
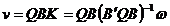 (24)
(24)
Insa:
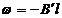
si in
consecinta:
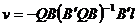
cu care:
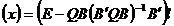 (25)
(25)
si in cele din
urma:
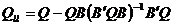 (26)
(26)
Pentru
calculul coeficientului de pondere al unei functii de marimi
masurate direct, supuse la conditii si de precizii diferite se
considera functia:
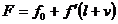
sau:
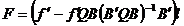 (27)
(27)
si:
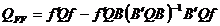
sau:
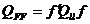 (28)
(28)