Rotorul
unei functii vectoriale
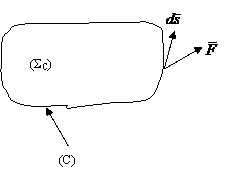
Se analizeaza integrala de linie pe un contur inchis
(C) a unei functii vectoriale 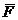 definita in
spatiul tridimensional. Curba inchisa (C) margineste o
infinitate de suprafete si se alege o suprafata oarecare
dintre acestea (fig.A.4.5.).
definita in
spatiul tridimensional. Curba inchisa (C) margineste o
infinitate de suprafete si se alege o suprafata oarecare
dintre acestea (fig.A.4.5.).
Denumirea intergalei de linie este circulatia functiei vectoriale 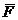 si se
noteaza:
si se
noteaza:
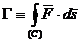 (A.4.17)
(A.4.17)
unde 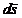 este elementul de drum
(un vector infinitezimal tangent la curba (C) in punctul respectiv).
este elementul de drum
(un vector infinitezimal tangent la curba (C) in punctul respectiv).
Fig.A.4.5.
Exista doua
sensuri de parcurgere a curbei (C); pentru a determina directia si
sensul lui 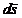 , se alege unul din ele. Se traverseaza suprafata (SC) pe drumul (B) formand doua bucle (C1)
si (C2), ambele cuprinzand drumul (B) (fig.A.4.6.). Se
observa ca:
, se alege unul din ele. Se traverseaza suprafata (SC) pe drumul (B) formand doua bucle (C1)
si (C2), ambele cuprinzand drumul (B) (fig.A.4.6.). Se
observa ca:
G G G (A.4.18)
deoarece:
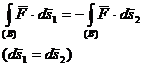 (A.4.19)
(A.4.19)
Fig.
A.4.6.
Daca se continua divizarea in bucle mai mici: C1, C2, . . . , Ck,
. . ., Cn suma integralelor nu se schimba:
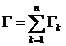 ,
,
adica:
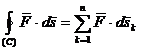 . (A.4.20)
. (A.4.20)
Se poate continua subdivizarea cu scopul ca la
limita sa se obtina o caracteristica cantitativa
locala a functiei vectoriale. Micsorand buclele, se
micsoreaza circulatia, dar si aria suprafetelor
delimitate de bucle, astfel incat se va considera raportul dintre
circulatia unei bucle si aria buclei.
Alegand 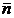 versorul
suprafetei
versorul
suprafetei 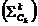 , limita (limita trebuie sa existe si sa fie
independenta de modul de divizare):
, limita (limita trebuie sa existe si sa fie
independenta de modul de divizare):
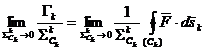 , (A.4.21)
, (A.4.21)
reprezinta o
marime scalara asociata punctului P aflat pe suprafata 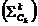 in functia
vectoriala
in functia
vectoriala 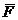 si directiei
si directiei 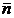 . Alegand trei directii independente
. Alegand trei directii independente 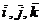 se obtin trei
numere diferite. Acestea pot fi considerate componentele unui vector numit rotor
se obtin trei
numere diferite. Acestea pot fi considerate componentele unui vector numit rotor 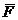 :
:
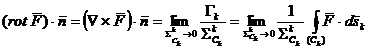 (A.4.22)
(A.4.22)
Se observa ca 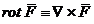 este o functie vectoriala de coordonate.
Directia vectorului rot
este o functie vectoriala de coordonate.
Directia vectorului rot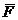 in orice punct, este normala la planul ce trece prin
acel punct pentru care marimea circulatiei este maxima.
in orice punct, este normala la planul ce trece prin
acel punct pentru care marimea circulatiei este maxima.
Marimea rotorului este egala cu valoarea
limita a circulatiei pe unitatea de arie a planului din jurul
punctului ales.
In coordonate carteziene, expresia rotorului
functiei 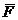 este:
este:
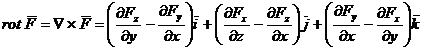 , (A.4.23)
, (A.4.23)
ce poate fi scrisa
si sub forma:
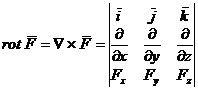 . (A.4.24)
. (A.4.24)
Pentru demonstrarea relatiilor (A.4.23) si
(A.4.24) se calculeaza, pentru inceput, rot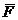 cand functia vectoriala
cand functia vectoriala 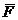 (x,y,z) este
data explicit pentru drumul ce delimiteaza un element de
suprafata dreptunghiulara, paralela cu planul xOy; in acest caz
(x,y,z) este
data explicit pentru drumul ce delimiteaza un element de
suprafata dreptunghiulara, paralela cu planul xOy; in acest caz 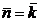 (fig.A.4.7 a, b). Integrala de linie a functiei
(fig.A.4.7 a, b). Integrala de linie a functiei 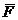 pe un asemenea drum
depinde de variatia lui Fx
cu y si de variatia lui Fy cu x.
pe un asemenea drum
depinde de variatia lui Fx
cu y si de variatia lui Fy cu x.
In aproximatia de ordinul intai, diferenta
dintre valoarea medie a lui Fx
pe segmentul de sus pentru y+Dy si valoarea medie pe
segmentul de jos pentru y este:
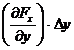 ,
,
deoarece la mijlocul
segmentului inferior:
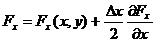 ;
;
iar la mijlocul
segmentului superior:
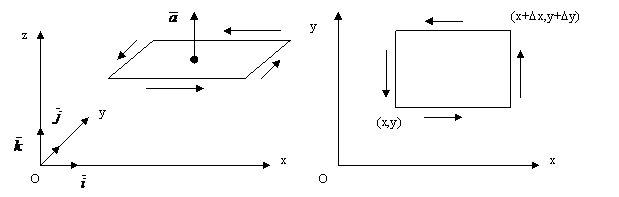
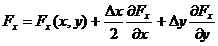
Fig.A.4.7.a Fig.A.4.7.b.
Contributia finala la circulatie este
data de produsul dintre diferenta valorilor medii si lungimea
elementului de drum x. Aceasta
contributie este egala cu 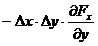 ; semnul minus aparand intrucat integrarea se face de la
dreapta la stanga pe latura de sus a dreptunghiului si, daca
componenta pozitiva Fx
este mai mare sus, ea da o contributie negativa in
circulatie. Contributia celorlalte laturi este
; semnul minus aparand intrucat integrarea se face de la
dreapta la stanga pe latura de sus a dreptunghiului si, daca
componenta pozitiva Fx
este mai mare sus, ea da o contributie negativa in
circulatie. Contributia celorlalte laturi este 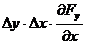 , semnul fiind plus deoarece componenta Fy este mai mare pe latura din dreapta; contributia
acestor laturi in circulatie fiind deci pozitiva.
, semnul fiind plus deoarece componenta Fy este mai mare pe latura din dreapta; contributia
acestor laturi in circulatie fiind deci pozitiva.
Pentru suprafata
dreptunghiulara considerata, circulatia functiei 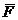 va fi:
va fi:
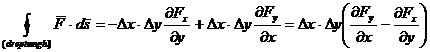 (A.4.25)
(A.4.25)
Cum Dx Dy este aria dreptunghiului,
conform definitiei (A.4.22), avem:
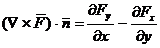 ; cand
; cand 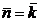 (A.4.26)
(A.4.26)
Analog, pentru 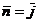 si
si 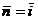 se obtine:
se obtine:
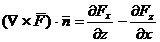 ; cand
; cand 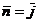 (A.4.27)
(A.4.27)
si respectiv:
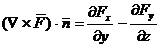 pentru
pentru 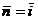 (A.4.28)
(A.4.28)
Cumuland relatiile
(A.4.26), (A.4.27), (A.4.28), in cazul general, se obtine, in final:
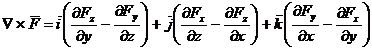 (A.4.29)
(A.4.29)


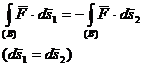 (A.4.19)
(A.4.19)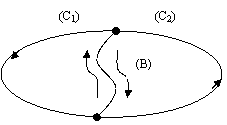
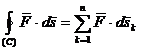 . (A.4.20)
. (A.4.20)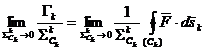 , (A.4.21)
, (A.4.21)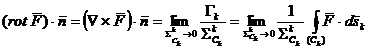 (A.4.22)
(A.4.22)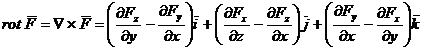 , (A.4.23)
, (A.4.23)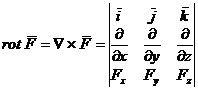 . (A.4.24)
. (A.4.24)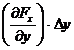 ,
,
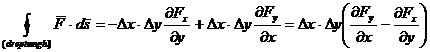 (A.4.25)
(A.4.25)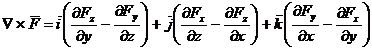 (A.4.29)
(A.4.29)