AJUSTAREA SI
Aproximarea datelor
Notiuni generale
Observatiile experimentale
sunt, in general, seturi de date discrete care, pot fi organizate ca vectori
coloana sau matrici, in care, liniile reprezinta rezultatele si
observatiile la un moment dat. Considerand ca s-au realizat
determinari ale traficului de autovehicule grele, in 24 de ore, prin trei
puncte diferite, aceste date pot fi stocate intr-o matrice cu dimensiunea 24x3:
»trafic=[11, 11, 9; 7, 13, 11; 14, 17, 20; 11, 13, 9; 43, 51, 69; 38, 46, 76; 61, 132, 186; 75, 135, 180; 38, 88, 115; 28, 36, 55; 12, 12, 14; 18, 27, 30; 18, 19, 29; 17, 15, 18; 19, 36, 48; 32, 47, 10; 42, 65, 92; 57, 66, 151; 44, 55, 90; 114, 145, 257; 35, 58, 68; 11, 12, 15; 13, 9, 15; 10, 9, 7]
trafic =
|
Ora
inregistrarii
|
Pct. A
|
Pct. B
|
Pct. C
|
|
01 h 00 min
|
|
|
|
|
02 h 00 min
|
|
|
|
|
03 h 00 min
|
|
|
|
|
04 h 00 min
|
|
|
|
|
05 h 00 min
|
|
|
|
|
06 h 00 min
|
|
|
|
|
07 h 00 min
|
|
|
|
|
08 h 00 min
|
|
|
|
|
09 h 00 min
|
|
|
|
|
10 h 00 min
|
|
|
|
|
11 h 00 min
|
|
|
|
|
12 h 00 min
|
|
|
|
|
13 h 00 min
|
|
|
|
|
14 h 00 min
|
|
|
|
|
15 h 00 min
|
|
|
|
|
16 h 00 min
|
|
|
|
|
17 h 00 min
|
|
|
|
|
18 h 00 min
|
|
|
|
|
19 h 00 min
|
|
|
|
|
20 h 00 min
|
|
|
|
|
21 h 00 min
|
|
|
|
|
22 h 00 min
|
|
|
|
|
23 h 00 min
|
|
|
|
|
24 h 00 min
|
|
|
|
11 11 9
7 13 11
14 17 20
11 13 9
43 51 69
38 46 76
61 132 186
75 135 180
38 88 115
28 36 55
12 12 14
18 27 30
18 19 29
17 15 18
19 36 48
32 47 10
42 65 92
57 66 151
44 55 90
114 145 257
35 58 68
11 12 15
13 9 15
10 9 7
Matricea
trafic, a observatiilor
zilnice, poate fi utilizata in analize si prelucrari matematice
ulterioare. In acest sens, presupunand necesara reprezentarea
grafica, pentru vizualizarea traficului, la un moment dat (considerand
reperele orare date de vectorul t=1:24),
se foloseste urmatoarea secventa MATLAB:
» t=1:24;
»
set(0, 'defaultaxeslinestyleorder', '-|--|-.');
»
set(0, 'defaultaxescolororder', [0 0 0]);
» xlabel('Timpul'), ylabel('Numar de
vehicule in trafic'), grid on
» plot(t, trafic), legend('Locatia
A', 'Locatia B', 'Locatia C', 0)
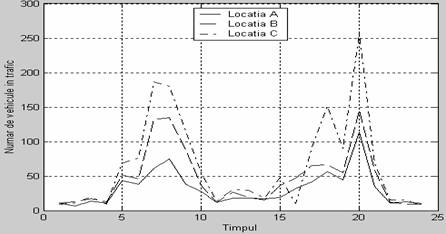
In
practica inginereasca este necesar, atat in analiza rezultatelor
experimentale, cat si pentru emiterea unor concluzii, ca datele
obtinute sa fie aproximate prin curbe polinomiale, exponentiale
sau de alta natura.
Utilizarea GUI (Graphical User
Interface- Interfata Grafica Utilizator)
pentru ajustarea datelor
Cea
mai rapida si eficienta procedura de ajustare, aproximare,
interpolare si extrapolare a datelor experimentale, este Interfata Grafica Utilizator (Graphical User Interface-GUI ),
disponibila in MATLAB, versiunile superioare (Release 12 sau 13).
Informatii complete, privind aceasta procedura, se regasesc
in documentatia de ajutor din meniul Help
optiunea Full Product Family
Help. Accesarea interfetei grafice (pentru simplificarea
exprimarii se va folosi, in continuare, sintagma GUI) pentru ajustarea
datelor, se introduce, in fereastra de comanda MATLAB, comanda:
» cftool
Aceasta comanda are ca
efect activarea interfetei grafice Curve
Fitting Tool (Instrument de ajustare a curbelor):
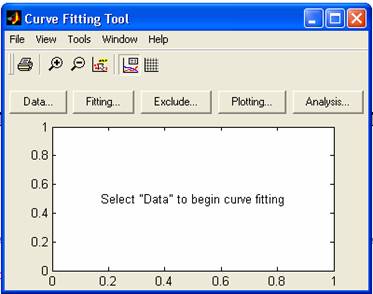
Daca
in fereastra de comanda a MATLAB, exista vectori coloana de
aceeasi dimensiune, acestia vor fi selectati automat de editorul
de ajustare si stocati in vederea prelucrarii. Altfel, se impune
introducerea sau importarea datelor in vectori coloana.
Procedura de ajustare
Procedura
de ajustare va fi prezentata aici pentru un caz specific: ajustarea
datelor cuprinse in doi vectori coloana y si t. Se
presupune ca in linia de comanda s-au introdus vectorii y si t:
» t = [0 .3 .8 1.1 1.6 2.3]'; y = [0.5 0.82
1.14 1.25 1.35 1.40]';
- -se introduce comanda pentru activarea
interfetei grafice a ajustarii:
» cftool
-Se acceseaza butonul Data care activeaza o interfata grafica ce
permite selectarea valorilor care urmeaza a fi ajustate pe axa X,
respectiv pe axa Y si ponderea acestor date (daca aceasta este "None"
valoarea ponderii este
implicit 1 ). Atunci cand se selecteaza un anumit vector pe o
axa, in medalion se reprezinta grafic valorile vectorului respectiv.
De asemenea aceasta
interfata permite definirea unui set nou de valori, un vector in functie de altul, de
exemplu, prin accesarea butonului Create
Data Set.
Se inchide sesiunea acestei interfete
grafice cu butonul Close.
- -Din interfata
grafica Curve Fitting Tool
se acceseaza butonul Fitting
al carui efect este deschiderea editorului de ajustare compus din
doua parti distincte: editorul propriu-zis, Fit Editor, si tabloul
ajustarilor, Table of Fits.
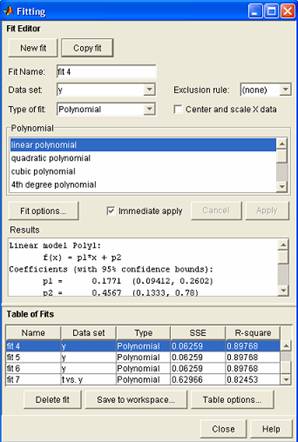
Editorul ajustarii , Fit Editor, permite actiuni
pentru:
- Specificarea numelui ajustarii curente, setarea
datelor curente si stabilirea regulii de excludere;
- Explorarea diferitelor metode de ajustare ale
seturilor de date curente, folosind o biblioteca de ecuatii,
metode de ajustare spline si interpolanti;
- Suprareglarea optiunilor implicite de ajustare
(cum ar fi metoda identificarii coeficientilor);
- Compararea rezultatelor ajustarii;
Tabloul
ajustarilor , Table of Fits,
permite
Monitorizarea datelor si ajustarilor
anterioare;
Afisarea unui sumar al rezultatelor
ajustarii;
Salvarea sau anularea rezultatelor
ajustarii.
Se
acceseaza butonul New fit care
aloca automat un nume implicit ajustariii curente. Presupunem ca
aceasta se va numi ajustarea_1, iar
cu urmatoarea optiune, Data
set, se defineste setul de date (presupunem ca acesta este setul t vs. y, adica vectorul t, in functie de y) care va fi ajustat in cele ce
urmeaza si va fi numit, in continuare, ajustarea_1. Se selecteaza un alt set de date, definit
anterior (presupunem ca acesta este setul y vs. t, adica vectorul y,
in functie de t), si
acesta va fi numit in continuare ajustarea_2.
Se alege aproximarea polinomiala, iar in urmatoarea sectiune se
va selecta ajustarea polinomiala cuadratica (printr-un polinom de
gradul doi: f(x)
= p1*x^2 + p2*x + p3). Se valideaza
optiunea Immediate apply, ceea
ce va avea drept efect afisarea rezultatelor in caseta Results. In paralel MATLAB
prelucreaza datele in functie de optiunile setate si
selectiile operate, fiind afisate, in fereastra interfetei
grafice Curve Fitting Tool reprezentarile
grafice ale celor doua seturi de date, atat cele discrete cat si cele
previzionate, ajustate.
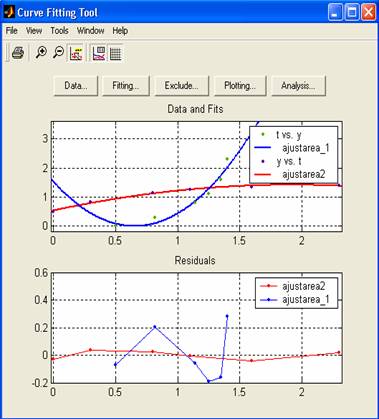
Din
meniul View al interfetei
grafice Curve Fitting Tool se
selecteaza optiunea Residuals-Line
Plot:
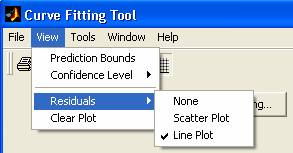
care permite, si realizeaza,
reprezentarea grafica a reziduurilor ajustarii, fiind data o
masura reala a marimii erorilor de aproximare, in diferite
puncte ale seturilor de date ajustate. Reprezentarea grafica a
reziduurilor arata ca o ajustare mai buna este posibila,
sau nu. In functie de marimea erorilor de calcul si a
distantei fata de valorile discrete efective, se poate lua
decizia unei ajustari ulterioare, pentru cresterea
calitatii aproximarii, prin metode si tehnici multiple.
Determinartea celei mai bune ajustari
Pentru
a determina cea mai buna ajustare sau aproximare trebuie avute in vedere
atat rezultatele grafice cat si rezultatele numerice ale procedurii
efective. Pentru exemplificare se considera ca pentru vectorul populatia_USA = [3.9, 5.3, 7.2, 9.6, 12.9, 17.1, 23.1, 31.4, 38.6, 50.2, 62.9, 76, 92, 105.7, 122.8, 131.7, 150.7, 179, 205, 226.5, 248.7]'
raportat la anii de referinta cuprinsi in vectorul anii_de_referinta=[1790, 1800, 1810, 1820, 1830, 1840, 1850, 1860, 1870, 1880, 1890, 1900, 1910, 1920, 1930, 1940, 1950, 1960, 1970, 1980, 1990]'
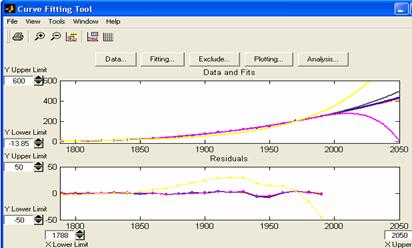
s-au realizat ajustari folosind expresii polinomiale de diferite grade
(2, 4 si 7) respectiv o ajustare exponentiala de un singur
termen, a*exp(b*x) (adica 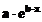 ), si s-au obtinut reprezentarile grafice (ale
rezultatelor ajustarii, respectiv ale reziduurilor), din figura:
), si s-au obtinut reprezentarile grafice (ale
rezultatelor ajustarii, respectiv ale reziduurilor), din figura:

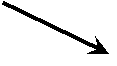
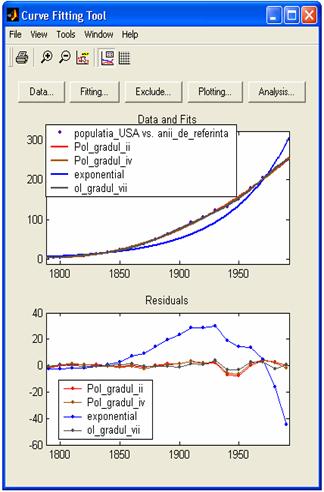
Din
aceste reprezentari se poate deduce ca este dificil a decide care
dintre polinoameofera cele mai bune rezultate pentru aproximare sau
ajustare, intrucat diferentele reziduale sunt nesemnificative, iar, prin
comparatie, ajustarea exponentiala cu un singur termen este
evident neacoperitoare, datorita gradului mare de incompatibilitate
si concordanta cu datele discrete.Setul de date ajustate se
poate vizualiza accesand butonul Data,
caseta Data sets, optiunea View:
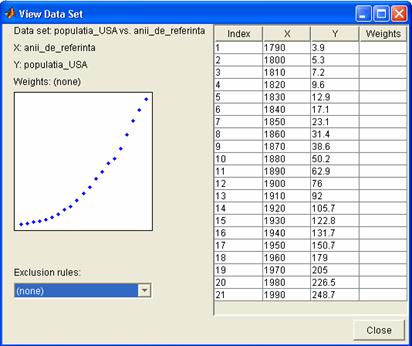
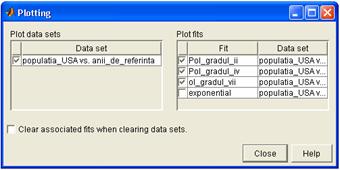
In
continuare, se foloseste interfata grafica Curve Fitting Tool, butonul Plotting
pentru a elimina metoda de ajustare printr-o functie
exponentiala, invalidand caseta corespunzatoare, aceasta
metoda dovedindu-se a fi neconcludenta pentru ajustarea datelor celor
doi vectori:
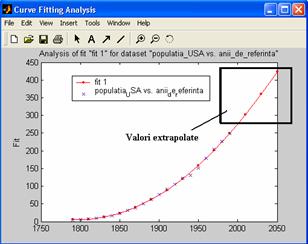
Pentru
a examina, datele extrapolate prin cele trei expresii polinomiale de diferite
grade, se vor modifica limitele axelor folosind meniul Tools, optiunea Axis
Limit, prin modificarea limitei superioare a limitei X Upper Limit la valoarea 2050,
ceea ce va permite extrapolarea, prin cele trei expresii polinomiale, a valorii
vectorului populatia_USA
corespunzatoare acestui an:
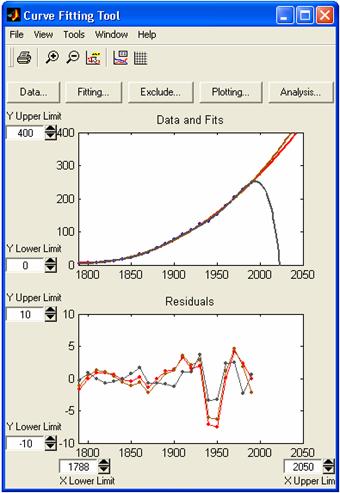
Se
constata ca extrapolarea printr-un polinom de gradul 7 va
genera o valoare extrapolata, pe baza datelor existente, mult
diferita de celelalte valori, demonstrand neconcordanta evidenta
cu datele extrapolate prin celelalte expresii polinomiale.
Acest
exemplu ilustreaza, foarte clar, ca alegerea unei metode de
extrapolare trebuie facuta cu mare atentie, in functie de
mai multi factori care ar putea influenta asupra corectitudinii
rezultatelor.
Examinarea rezultatelor numerice
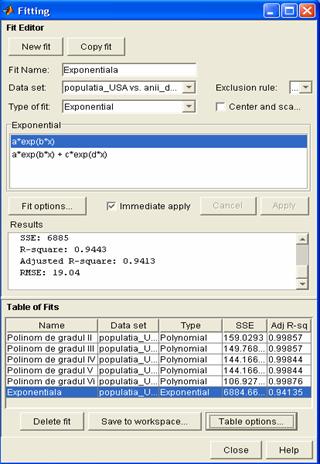 Examinarea reprezentarilor
grafice ale aproximarilor, din exemplul anterior, demonstreaza
ca este necesara o procedura suplimentara pentru a decide
care dintre variantele alese pentru ajustarea datelor din vectorul populatia_USA este varianta cea mai apropiata de varianta
corecta. Pentru aceasta este nevoie de studiul rezultatelor numerice,
care sunt asociate procedurii de aproximare propriu-zisa. MATLAB
ofera doua tipuri de rezultate numerice, afisate in
interfata grafica Curve
Fitting Tool ->Fitting ->Results si Table of Fits: concordanta
rezultatelor aproximarii respectiv intervalul
de confidenta. Concordanta rezultatelor arata cat de bine sunt aproximate datele, iar
intervalul de confidenta reflecta precizia rezultatelor. Pentru
a evidentia rezultatele numerice ale ajustarii datelor, se
considera ajustarea polinomiala de grad 2, 3, 4, 5 si 6, respectiv
aproximarea exponentiala cu un singur termen, a datelor
continute in vectorul populatia_USA,
relativ la vectorul anii_de_referinta,
pentru care s-au obtinut rezultatele numerice din figura
alaturata:
Examinarea reprezentarilor
grafice ale aproximarilor, din exemplul anterior, demonstreaza
ca este necesara o procedura suplimentara pentru a decide
care dintre variantele alese pentru ajustarea datelor din vectorul populatia_USA este varianta cea mai apropiata de varianta
corecta. Pentru aceasta este nevoie de studiul rezultatelor numerice,
care sunt asociate procedurii de aproximare propriu-zisa. MATLAB
ofera doua tipuri de rezultate numerice, afisate in
interfata grafica Curve
Fitting Tool ->Fitting ->Results si Table of Fits: concordanta
rezultatelor aproximarii respectiv intervalul
de confidenta. Concordanta rezultatelor arata cat de bine sunt aproximate datele, iar
intervalul de confidenta reflecta precizia rezultatelor. Pentru
a evidentia rezultatele numerice ale ajustarii datelor, se
considera ajustarea polinomiala de grad 2, 3, 4, 5 si 6, respectiv
aproximarea exponentiala cu un singur termen, a datelor
continute in vectorul populatia_USA,
relativ la vectorul anii_de_referinta,
pentru care s-au obtinut rezultatele numerice din figura
alaturata:
Parametrii
numerici ai ajustarii se pot seta din interfata Curve Fitting Tool ->Fitting ->Results si Table of Fits->Table options:
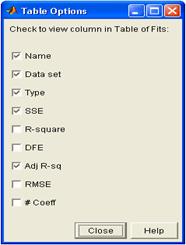
In
aceasta sesiune sunt validate titlurile coloanelor care vor aparea
in tabelul Table of Fits. Optiunea SSE
(Sum of Squares Due to Error), este
o marime statistica ce se refera la marimea deviatiei
valorii de raspuns a ajustarii, fata de valoarea data,
calculata ca suma patratelor erorilor in functie de marimea
reziduurilor. Acest parametru este definit prin ecuatia 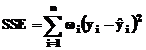 , in care
, in care 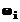 reprezinta
marimea reziduului (determinate, si afisate, in MATLAB, cu
optiunea Residuals din meniul View):
reprezinta
marimea reziduului (determinate, si afisate, in MATLAB, cu
optiunea Residuals din meniul View):
iar yi si 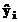 sunt datele aproximate
respectiv previzionate. Valorile reziduale se pot determina daca se
cunoaste varianta datelor (
sunt datele aproximate
respectiv previzionate. Valorile reziduale se pot determina daca se
cunoaste varianta datelor (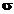 ), cu relatia
), cu relatia 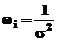 , sau se poate aproxima cu relatia
, sau se poate aproxima cu relatia  , daca nu se cunoaste varianta datelor, in
care
, daca nu se cunoaste varianta datelor, in
care 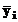 reprezinta
valoare medie evaluata statistic.
reprezinta
valoare medie evaluata statistic.
R-square reprezinta
raportul dintre suma patratelor regresiilor (sum of squares of the regression -SSR) si suma totala a patratelor (total sum of squares -SST):  . R-square poate
lua valori cuprinse intre 0 si 1, o valoare mai aproape de 1 are
semnificatia unei bune aproximari. De exemplu, o valoare R-square=0, 99871 (in cazul
ajustarii polinomiale de gradul II) arata ca exista o
variatie de pana la 99, 87 % fata de valoarea medie
calculata.
. R-square poate
lua valori cuprinse intre 0 si 1, o valoare mai aproape de 1 are
semnificatia unei bune aproximari. De exemplu, o valoare R-square=0, 99871 (in cazul
ajustarii polinomiale de gradul II) arata ca exista o
variatie de pana la 99, 87 % fata de valoarea medie
calculata.
Parametrul DFE (Degrees of Freedom
Adjusted R-Square) foloseste parametrul R-square, definit anterior, si ajusteaza aceasta
valoare pe baza gradelor de libertate ale
reziduurilor. Gradele de libertate ale reziduurilor se reprezinta
diferenta dintre numarul valorilor de raspuns si numarul
coeficientilor de aproximare: v=n-m.
In aceasta relatie, v
reprezinta numarul datelor independente din totalul de n puncte necesare calcularii sumei
de patrate, iar m este
numarul de coeficienti ai ecuatiei de aproximare. Modelul
matematic, se considera ca fiind un bun indicator statistic al
calitatii aproximarii cand sunt adaugati
coeficienti suplimentari in ecuatia aproximarii.
Parametrul RMSE (Root Mean Squared
Error) este cunoscut ca eroarea standard a aproximarii
si ca eroarea standard a regresiilor. Se determina cu relatia: 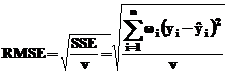 . O valoare apropiata de 0 inseamna o buna
aproximare.
. O valoare apropiata de 0 inseamna o buna
aproximare.
Validarea
parametrului #Coeff are ca efect
afisarea numarului de coeficienti folositi pentru
aproximarea datelor.
Intervalul de confidenta
(de siguranta) reprezinta limitele, inferioara
respectiv superioara, ale coeficientilor ecuatiei
aproximarii. Formatul afisat pentru un parametru este: p1 = 0.006541 (0.006124, 0.006958),
ceea ce inseamna ca valoarea calculata a coeficientului este 0.006541, limita inferioara 0.006124 respectiv limita
superioara 0.006958. Implicit, nivelul de siguranta este 95%, si se poate modifica din
interfata Curve Fitting Tool meniul View, optiunea Confidence
level. Limitele de siguranta pot fi calculate si
afisate grafic din interfata Curve
Fitting Tool meniul View, optiunea Prediction Bounds, sau cu optiunea
Analysis din interfata Curve Fitting Tool.
Salvarea rezultatelor ajustarii
Din
interfata Fitting, accesand
butonul Save to workspace, se
salveaza intregul proces de ajustare, prin validarea celor trei
optiuni:
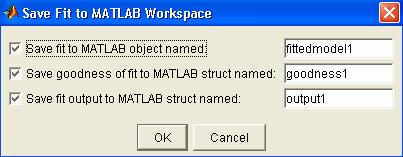
prima optiune salveaza ajustarea ca
obiect MATLAB

a doua optiune salveaza, intr-o
structura multidimensionala, concordanta ajustarii:
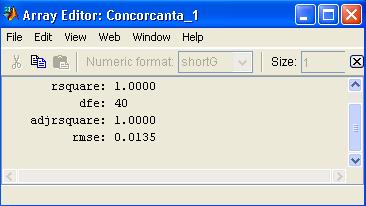
cea de-a treia optiune salveaza
rezultatele ajustarii, oferind informatii asupra parametrilor
numerici ai ajustarii
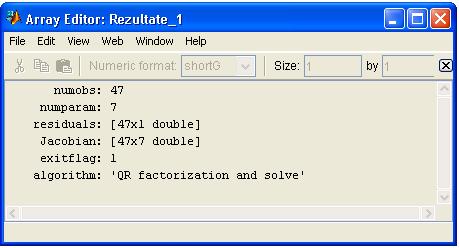
Analiza rezultatelor ajustarii
Din
interfata Curve Fitting Tool, butonul Analysis se pot realiza analize ale
parametrilor ajustarii, in functie de datele originale. Se pot
interpola, extrapola date, se pot diferentia si integra curbele de
variatie ale ajustarii, intre anumite limite. Pentru aceasta, se
scceseaza vectorul Xi dorit,
din campul Analyze at Xi, se
selecteaza caseta aferenta evaluarii Evaluate fit at Xi, pentru afisarea rezultatelor si
reprezentarea grafica a acestora fiind necesara validarea casetelor Plot results si Plot data set, dupa care se
acceseaza butonul Apply, pentru
realizarea procedurii. De exemplu pentru extrapolarea necesara
identificarii datelor ajustarii folosind ajustarea polinomiala, pentru
populatia corespunzatoare anului 2025, se va modifica ultima valoare
din campul Analyze at Xi, la
valoarea 2025:
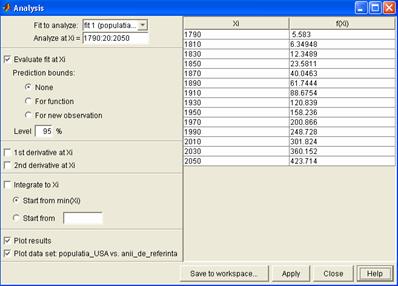
Rezultatele extrapolarii se
pot salva, similar procesului de ajustare propriu-zisa
Exemplu: Se va
realiza o ajustare polinomiala de ordinul III, V si VI, pentru
vectorii x = [4:0.1:7 9:0.2:12]', y = c(1) + c(2)*x + c(3)*x.^2 + c(4)*x.^3 + (rand(size(x))-0.5), ai
carui coeficienti sunt elementele vectorului c = [8 -5 13 12].
»x = [4:0.1:7
9:0.2:12]' ; c = [8 -5 13 12]; y = c(1) +
c(2)*x + c(3)*x.^2 + c(4)*x.^3
+ (rand(size(x))-0.5);
»cftool
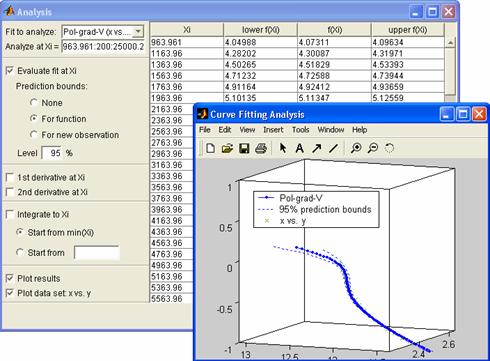
Urmand
procedura enuntata, se realizeaza ajustarea cu cele trei curbe
polinomiale. Analiza rezultatelor permite, din interfata Curve Fitting Analysis, manevre ale
reprezentarii grafice, utilizand facilitatile de prelucrare
si animatie a figurilor, permise de MATLAB Release 12 si
superioare acesteia:
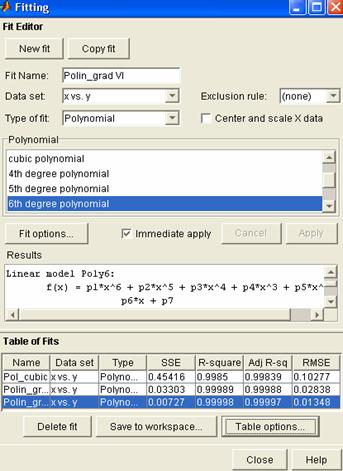
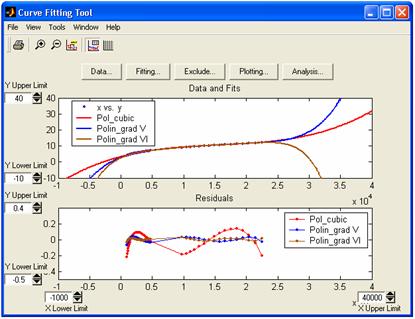
Exemplu:
Se va ajusta o
curba de variatie a coeficientului de dilatare a Cu, in raport cu
temperatura. Pentru aceasta se va considera vectorul temp al temperaturilor, un vector cu 236 elemente, cu temperaturi
cuprinse intre 24, 41 [K] si 848, 23 [K], iar valorile masurate
experimental, pentru coeficientul de dilatare, pentru aceste temperaturi,
stocate in vectorul coloana coef_CU.
Se va realiza o aproximare rationala, cu o functie avand atat
numaratorul cat si numitorul, polinoame de gradul doi. Dupa
ce sunt introduse datele, in fereastra de comanda (prin una din
optiunile posibile:de la tastatura, import, incarcare etc.), se
activeaza procesul de ajustare, cu functia cftool, apoi se seteaza parametrii de aproximare din
interfata Fitting,
selectand, din campul Type of fit,
optiunea Rational. Apoi, se
nominalizeaza tipul polinomului de la numarator (Numerator), respectiv de la numitorul
expresiei rationale (Denominator):
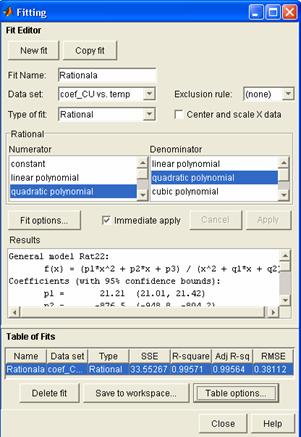
Folosind
butonul Table options, se
valideaza parametrii numerici ai ajustarii, parametri care vor fi
cuprinsi in tabelul Table of Fits.
Afisarea rezultatelor si reziduurilor ajustarii se
realizeaza selectand optiunea Residuals-Plot
line, din meniul View al
interfetei grafice Curve Fitting Tool:
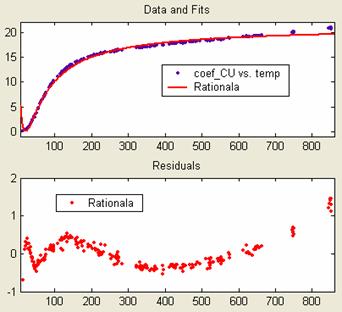
Este
usor de observat ca sunt "zone" in care aproximarea nu este
acoperitoare: lipsesc parametrii si rezultatele ajustarii:
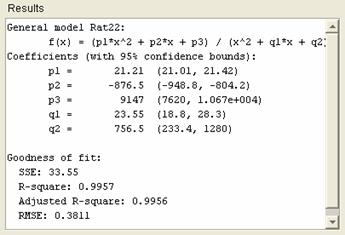
Se
incearca, in consecinta o alta ajustare, de tipul
rationala polinomiala cu polinoame de gradul III, atat la
numarator cat si la numitor:
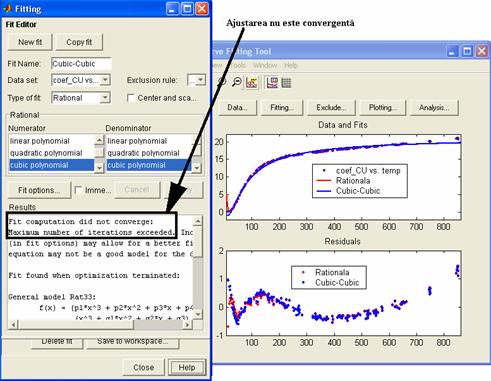
 Acest tip de aproximare, se observa din
interfata Fit Editor campul Results, este neconvergenta, ceea ce anuleaza posibilitatea
alegerii unei astfel de ajustari pentru acest set de date, fiind, astfel
necesara o alta ajustare.
Acest tip de aproximare, se observa din
interfata Fit Editor campul Results, este neconvergenta, ceea ce anuleaza posibilitatea
alegerii unei astfel de ajustari pentru acest set de date, fiind, astfel
necesara o alta ajustare.
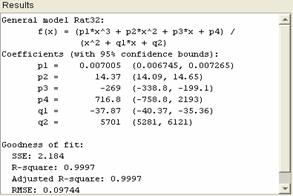
Modificarea
expresiei rationale de ajustare, astfel incat polinomul de la
numarator sa fie de gradul III, iar cel de la numitor, de gradul
II, are ca rezultat o aproximare mult imbunatatita,
reziduurile fiind aleatoriu distribuite fata de valoarea zero, ceea
ce inseamna o ajustare realista:
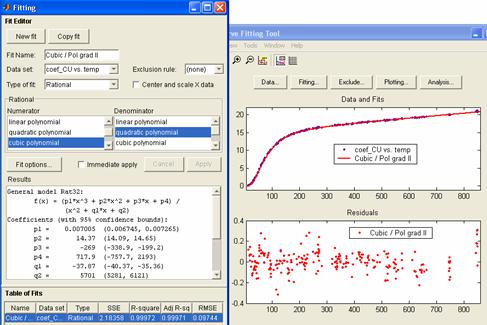
In
campul Results al interfetei Fit Editor, sunt prezentati
parametrii ajustarii, si coeficientii modelului matematic al
acesteia. Interfata Curve Fitting
Tool, prezinta, in campul Residuals,
dispersia cvasi-uniforma a reziduurilor, in raport cu "linia zero". Acest
aspect al dispersiei este o masura a unei aproximari corecte
si valabila pentru acest set de date.












 Examinarea reprezentarilor
grafice ale aproximarilor, din exemplul anterior, demonstreaza
ca este necesara o procedura suplimentara pentru a decide
care dintre variantele alese pentru ajustarea datelor din vectorul populatia_USA este varianta cea mai apropiata de varianta
corecta. Pentru aceasta este nevoie de studiul rezultatelor numerice,
care sunt asociate procedurii de aproximare propriu-zisa. MATLAB
ofera doua tipuri de rezultate numerice, afisate in
interfata grafica Curve
Fitting Tool ->Fitting ->Results si Table of Fits: concordanta
rezultatelor aproximarii respectiv intervalul
de confidenta. Concordanta rezultatelor arata cat de bine sunt aproximate datele, iar
intervalul de confidenta reflecta precizia rezultatelor. Pentru
a evidentia rezultatele numerice ale ajustarii datelor, se
considera ajustarea polinomiala de grad 2, 3, 4, 5 si 6, respectiv
aproximarea exponentiala cu un singur termen, a datelor
continute in vectorul populatia_USA,
relativ la vectorul anii_de_referinta,
pentru care s-au obtinut rezultatele numerice din figura
alaturata:
Examinarea reprezentarilor
grafice ale aproximarilor, din exemplul anterior, demonstreaza
ca este necesara o procedura suplimentara pentru a decide
care dintre variantele alese pentru ajustarea datelor din vectorul populatia_USA este varianta cea mai apropiata de varianta
corecta. Pentru aceasta este nevoie de studiul rezultatelor numerice,
care sunt asociate procedurii de aproximare propriu-zisa. MATLAB
ofera doua tipuri de rezultate numerice, afisate in
interfata grafica Curve
Fitting Tool ->Fitting ->Results si Table of Fits: concordanta
rezultatelor aproximarii respectiv intervalul
de confidenta. Concordanta rezultatelor arata cat de bine sunt aproximate datele, iar
intervalul de confidenta reflecta precizia rezultatelor. Pentru
a evidentia rezultatele numerice ale ajustarii datelor, se
considera ajustarea polinomiala de grad 2, 3, 4, 5 si 6, respectiv
aproximarea exponentiala cu un singur termen, a datelor
continute in vectorul populatia_USA,
relativ la vectorul anii_de_referinta,
pentru care s-au obtinut rezultatele numerice din figura
alaturata:
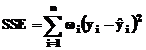 , in care
, in care 
 , daca nu se cunoaste varianta datelor, in
care
, daca nu se cunoaste varianta datelor, in
care  . R-square poate
lua valori cuprinse intre 0 si 1, o valoare mai aproape de 1 are
semnificatia unei bune aproximari. De exemplu, o valoare R-square=0, 99871 (in cazul
ajustarii polinomiale de gradul II) arata ca exista o
variatie de pana la 99, 87 % fata de valoarea medie
calculata.
. R-square poate
lua valori cuprinse intre 0 si 1, o valoare mai aproape de 1 are
semnificatia unei bune aproximari. De exemplu, o valoare R-square=0, 99871 (in cazul
ajustarii polinomiale de gradul II) arata ca exista o
variatie de pana la 99, 87 % fata de valoarea medie
calculata.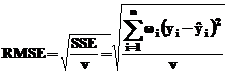 . O valoare apropiata de 0 inseamna o buna
aproximare.
. O valoare apropiata de 0 inseamna o buna
aproximare.












 Acest tip de aproximare, se observa din
interfata Fit Editor campul Results, este neconvergenta, ceea ce anuleaza posibilitatea
alegerii unei astfel de ajustari pentru acest set de date, fiind, astfel
necesara o alta ajustare.
Acest tip de aproximare, se observa din
interfata Fit Editor campul Results, este neconvergenta, ceea ce anuleaza posibilitatea
alegerii unei astfel de ajustari pentru acest set de date, fiind, astfel
necesara o alta ajustare. 