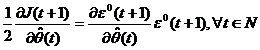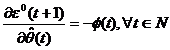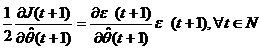Algoritm de identificare de tip gradient

Algoritm de identificare de tip gradient

Algoritmul de adaptare parametrica functioneaza in acest caz, bazat pe calculul gradientului unui criteriu patratic, exprimat in functie de eroarea de predictie si are ca obiectiv minimizarea acestui criteriu.

Consideram un proces cu parametri necunoscuti. Modelul discretizat al procesului, in reprezentare polinomiala, se scrie:

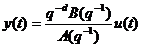tIN   (3.1)

cu:

A(q^-1)=1+a₁q^-1+ . . +a_nA q^-nA

B(q^-1)=b₁q^-1+ . . +b_nB q^-nB

care este redat si sub forma:

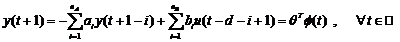(3.2)

unde:

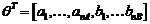(3.3)

este vectorul parametriilor procesului si

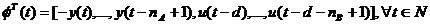(3.4)

este vectorul masuratorilor (observatiilor).

Modelul de predictie ajustabil a priori este dat de expresia:

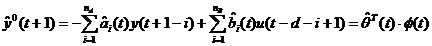tIN, (3.5)

unde:

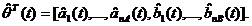(3.6)

este vectorul estimatiilor modelului.

Definim o eroare de predictie a priori,

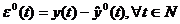(3.7)

si o eroare de predictie a posteriori,

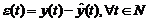(3.8)

Cautam un algoritm de adaptare parametrica recursiv si cu memorie. Structura unui asemenea algoritm este urmatoarea:

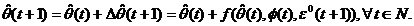   (3.9)

Termenul de corectie f(*) depinde doar de informatiile disponibile cel mult la momentul t+1 (ultima masuratoare y(t+1), parametrii 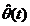si eventual de un numar finit de informatii la momentele t, t-1, t-2, . t-n). Trebuie minimalizata la fiecare pas, functia criteriu J, dupa relatia:

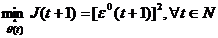(3.10)

Solutia se obtine printr-o procedura iterativa de tip gradient.

Algoritmul de adaptare parametrica corespunzator va avea forma:

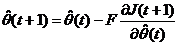(3.11)

unde F=aI a > 0, este amplificarea de adaptare matriciala (I - matrice diagonala unitara) si 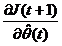este gradientul criteriului din ecuatia (3.10) raportat la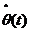

Din ecuatia (3.10), se obtine :

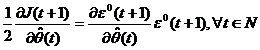(3.12)

Avem:

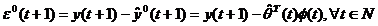(3.13)

si deci:

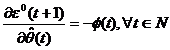(3.14)

Introducand ecuatia (3.14) in ecuatia (3.12), algoritmul de adaptare parametrica din (3.11) devine:

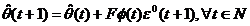(3.15)

Doua alegeri sunt posibile pentru F:

F aI a>0;.

sau,

F>0 (matrice pozitiv definita).

Algoritmul de adaptare parametrica dat in ecuatia (3.15) prezinta riscuri de oscilatie daca amplificarea de adaptare (respectiv a) este mare. Pentru a evita aceasta problema de instabilitate, folosim aceeasi abordare a gradientului, dar consideram un algoritm care foloseste  un criteriu exprimat in functie de eroarea de predictie a posteriori:

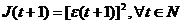(3.16)

Obtinem deci:

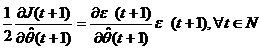(3.17)

Din ecuatiile (3.5) si (3.8) avem:

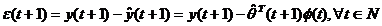(3.18)

si respectiv,

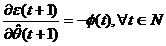(3.19)

Din ecuatiile (3.19) si (3.17), algoritmul de adaptare parametrica exprimat prin relatia (3.11) devine:

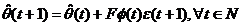(3.20)

Acest algoritm depinde de 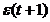, care este o functie de 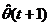. Pentru a putea justifica noua valoare de performanta a acestui algoritm, trebuie exprimat 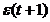in functie de .

Ecuatia (3.18) se poate rescrie:

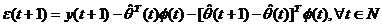(3.21)

Primii doi termeni ai membrului drept corespund lui si din ecuatia (3.20), avem:

,

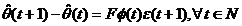ceea ce permite rescrierea ecuatiei (3.21) sub forma :

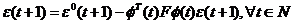(3.22)

din care obtinem relatia dorita intre 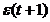si :

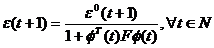(3.23)

si algoritmul ecuatiei (3.20) devine:

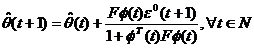(3.24)

Acesta este un algoritm stabil pentru o matrice de amplificare F pozitiv- definita. Impartirea prin 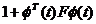ca in (3.20), introduce un efect de normare, care are ca rezultat imediat reducerea sensibilitatii algoritmului fata de eroarea si vectorul 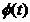.