Rezolvarea ecuatiilor
simbolice
Ecuatii
algebrice
Rezolvarea ecuatiilor algebrice
simple comporta, in MATLAB, un volum de lucru redus, dar necesita un
efort de calcul relativ mare pentru sistemul de calcul, comparativ cu alte
operatii si calcule matematice. Functia MATLAB folosita
pentru rezolvarea directa a ecuatiilor algebrice, este solve(), in care parametrii de intrare
sunt ecuatiile simbolice. Daca ecuatia are forma f(x)=0, atunci functia MATLAB se
apeleaza in forma simpla: solve(f(x)),
in timp ce, pentru ecuatii de forma f(x)=g(x),
functia MATLAB se apeleaza cu parametrii de intrare marcati ca
siruri de caractere: solve('f(x)=g(x)').
In cazul sistemelor de ecuatii, se respecta ultima regula de
scriere a parametrilor de intrare, ecuatiile fiind considerate siruri
de caractere separate prin caracterul virgula: solve('f1(x)=g1(x)', 'f2(x)=g2(x)',
'f3(x)=g3(x)', . ,'fn(x)=gn(x)').
In continuare se prezinta exemple ilustrative:
»
syms a x
»
solve(x^4-7*x^3+19*x^2-23*x+10)
ans
=
[ 1]
[ 2]
[
2+i]
[
2-i]
»
solve('x^2=6*x-5')
ans
=
[
1]
[
5]
Rezolvarea sistemului de
ecuatii 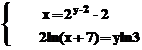 este realizabila
cu urmatoarea secventa:
este realizabila
cu urmatoarea secventa:
»syms
x y
»
[x,y]=solve('x=2^(y-2)-2','2*log(x+7)=y*log(3)')
x
=
1/4*exp(2.7726)-2
y
=
2.7726/log(2)
In scrierea solutiei acestui sistem de
ecuatii, MATLAB foloseste transformarea ln 16 =2,7726. Astfel, solutia sistemului se mai poate
scrie sub forma consacrata 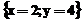 .
.
Rezolvarea ecuatiilor
parametrice sau a sistemelor cu numar mare de ecuatii, MATLAB
afiseaza un "camp" "S" al
solutiilor. "Extragerea" solutiilor din acest "camp" se realizeaza
folosind o instructiune simpla:S.(nume_solutie).
Pentru ilustrarea acestor situatii, se studiaza rezolvarea
sistemelor: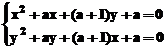 ;
; 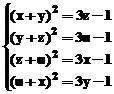 . Secventa urmatoare rezolva primul sistem:
. Secventa urmatoare rezolva primul sistem:
»syms
x y a
» S=solve('x^2+a*x+(a+1)*y=-a','y^2+a*y+(a+1)*x=-a')
S
=
x: [4x1 sym]
y: [4x1 sym]
"Campul" solutiilor sistemului,
S, este o matrice simbolica
formata din cele doua linii si o coloana a solutiilor
pentru x, respectiv pentru y. Afisarea
"desfasurata" a solutiilor, se poate realiza cu
instructiunea, data in linia de comanda:
» Solutiile=[S.x,S.y]
Solutiile
=
[ 1/2-1/2*(-3-8*a)^(1/2), 1/2+1/2*(-3-8*a)^(1/2)]
[ 1/2+1/2*(-3-8*a)^(1/2), 1/2-1/2*(-3-8*a)^(1/2)]
[-a-1/2+1/2*(4*a^2+1)^(1/2),-a-1/2+1/2*(4*a^2+1)^(1/2)]
[
-a-1/2-1/2*(4*a^2+1)^(1/2), -a-1/2-1/2*(4*a^2+1)^(1/2)]
Pentru rezolvarea celui de-al doilea
sistem se foloseste secventa:
»
syms x y z u
»S=solve('(x+y)^2=3*z-1','(y+z)^2=3*u-1','(z+u)^2=3*x- 1','(u+x)^2=3*y-1')
S
=
u: [2x1 sym]
x: [2x1 sym]
y: [2x1 sym]
z: [2x1 sym]
iar afisarea
detaliata a solutiilor este data cu comanda:
» solutii=[S.x,S.y,S.z,S.u]
solutii =
[3/8+1/8*i*7^(1/2), 3/8+1/8*i*7^(1/2), 3/8+1/8*i*7^(1/2), 3/8+1/8*i*7^(1/2)]
[3/8-
1/8*i*7^(1/2), 3/8- 1/8*i*7^(1/2), 3/8- 1/8*i*7^(1/2), 3/8- 1/8*i*7^(1/2)]
Rezolvarea ecuatiilor diferentiale
Rezolvarea ecuatiilor
diferentiale ordinare este posibila in MATLAB, folosind functia
dedicata dsolve(), in care,
parametrii de intrare sunt ecuatia diferentiala, scrisa
simbolic (folosind conventia de scriere a sirurilor de caractere),
respectiv conditiile la limita, daca acestea exista.
Parametrii de intrare se separa prin caracterul virgula.
Diferentiala de ordinul n se
specifica in ecuatie prin simbolul Dny, in care, D
reprezinta simbolizarea diferentialei, n reprezinta ordinul acesteia, iar y este integrala functiei, sau variabila dependenta (de
exemplu, D2y reprezinta diferentiala
de ordinul doi a functiei y). Variabila independenta
implicita, recunoscuta de MATLAB, este t. Aceasta variabila poate fi schimbata, prin
adaugarea, ca parametru de intrare, in sirul parametrilor
functiei MATLAB dsolve('ecuatie','cond_la_lim_1','con_la_lim_2','variabila_indep_noua').
De exemplu, rezolvarea ecuatiilor diferentiale: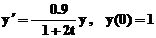 , respectiv
, respectiv
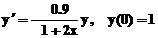 , este similara, cu observatia ca, in cel
de-al doilea caz, este necesara marcarea ca variabila
independenta, a variabilei x.
Acest lucru se va observa, in linia de comanda, in sirul parametrilor
de intrare. Secventa MATLAB, pentru rezolvarea acestor ecuatii
diferentiale, este:
, este similara, cu observatia ca, in cel
de-al doilea caz, este necesara marcarea ca variabila
independenta, a variabilei x.
Acest lucru se va observa, in linia de comanda, in sirul parametrilor
de intrare. Secventa MATLAB, pentru rezolvarea acestor ecuatii
diferentiale, este:
»
syms x y t
» y1=dsolve('Dy=-y*(0.9/(1+2*t))','y(0)=1')
y1
=
1/(1+2*t)^(9/20)
respectiv, pentru
a doua ecuatie:
»
y2=dsolve('Dy=-y*(0.9/(1+2*x))','y(0)=1','x')
y2
=
1/(1+2*x)^(9/20)
Rezolvarea ecuatiei a doua,
fara a specifica faptul ca x este
variabila independenta, are ca rezultat:
» y3=dsolve('Dy=-y*(0.9/(1+2*x))','y(0)=1')
y3
=
exp(-9/10/(1+2*x)*t)
Folosind conventia de scriere
comuna, solutiile sunt: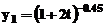 ;
; 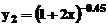 respectiv
respectiv 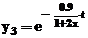 .
.
Exemple de utilizare a operatorilor
si functiilor MATLAB de baza
1).-Calculul puterii unui numar:
Sa se calculeze: 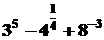
In MATLAB, se foloseste algoritmul:
E1=3^5-4^(1/4)+8^(-3)
ceea ce are ca rezultat:
E1
=
241.5877
2).-Calculul expresiilor cu numere irationale
Sa se calculeze expresiile:
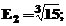
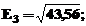

In MATLAB, se foloseste algoritmul:
» E2=15^(1/3) [Enter]
E2 =
2.4662
» E3=sqrt(43.56) [Enter]
E3 =
6.6000
» E4=((18-45*(2/88.9))^(1/3)+sqrt(23))^2-99^(1/8) [Enter]
E4 =
52.4891
3).- Calculul expresiilor exponentiale si logaritmice
Sa se calculeze :
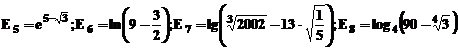
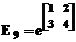
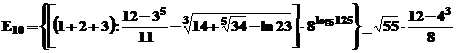
In MATLAB, aceste
expresii se calculeaza astfel:
» E5=exp(5-sqrt(3))
E5 =
26.2574
» E6=log(9-3/2)
E6 =
2.0149
»
E7=log10(2002^(1/3)-13*sqrt(1/5))
E7 =
0.8318
» E8=(log(90-3^(1/4)))/(log(4))
E8 =
3.2353
Pentru calculul expresiei 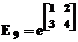 , se procedeaza astfel :
, se procedeaza astfel :
-se introduce, de la
tastatura:
»x=[1,2;3,4];
-se
determina valoarea expresiei, folosind functia exp
»E9=exp(x)
E9 =
2.7183 7.3891
20.0855 54.5982
O alta
posibilitate de a calcula aceasta expresie este prin aplicarea directa a
functiei MATLAB exp(), matricei
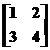 :
:
»E9=exp([1,2;3,4])
De observat ca rezultatul este o matrice
cu doua linii si doua coloane, exact ca si exponentul.
Expresia E10 se
calculeaza astfel:
»E10=(((1+2+3)/((12-3^5)/11)-(14+(34)^(1/5) .
-log(23))^(1/3))*8^((log(125))/(log(5))))-sqrt(55)*(12-4^3)/(8)
E10 =
-1.2985e+003
OBSERVATII:
Pentru calculul expresiilor irationale
(radicali cu indice diferit de 2: 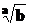 sau
sau 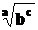 ) se foloseste algoritmul pentru calculul puterilor cu
exponent rational :
) se foloseste algoritmul pentru calculul puterilor cu
exponent rational : 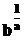 sau
sau 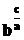 ;
;
Pentru calculul exponentialei ( 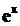 ) nu se foloseste
operatorul putere ("^");
) nu se foloseste
operatorul putere ("^");
Pentru calculul expresiilor logaritmice cu
logaritmi in alta baza decat baza naturala ( ln x) sau 10 ( lg x ) se foloseste formula de schimbare a bazei logaritmului
: 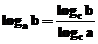
MATLAB dispune de o serie de combinatii,
implicite, de taste pentru crearea comenzilor rapide (conform tabelului):
|
tasta
|
combinaTia
de taste
|
semnificatia
|
|
|
Ctrl+p
|
Readuce
linia anterioara (prin actionarea repetata a tastei
"sageata sus" se readuc toate liniile anterioare, in linia
curenta)
|
|
|
Ctrl+n
|
Readuce
linia urmatoare (prin actionarea repetata a tastei
"sageata jos" se readuc toate liniile "urmatoare", in linia
curenta)
|
|
|
Ctrl+b
|
Salt
la stanga cu un caracter
|
|
|
Ctrl+f
|
Salt
la dreapta cu un caracter
|
|
Ctrl+
|
Ctrl+r
|
Salt
la dreapta, peste un cuvant
|
|
Ctrl+
|
Ctrl+l
|
Salt
la stanga, peste un cuvant
|
|
Home
|
Ctrl+a
|
Salt
la inceputul liniei de comanda
|
|
End
|
Ctrl+e
|
Salt
la sfarsitul liniei de comanda
|
|
Esc
|
Ctrl+u
|
Sterge
linia curenta
|
|
Del
|
Ctrl+d
|
Sterge
caracterul din dreapta cursorului
|
|
Backspace
|
Ctrl+h
|
Sterge
caracterul din stanga cursorului
|
|
Ctrl+k
|
Sterge
de la cursor pana la sfarsitul liniei de comanda curente.
|
APLICATII
Sa
se introduca de la tastatura, urmatoarele matrici :
A=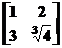 B=
B=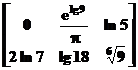 C=
C=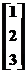 D=
D=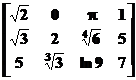
Sa
se scrie numarul :
in formatele: "scurt", "lung", "cu virgula mobila - scurt = eng. scurt", "cu virgula mobila - lung
=eng. lung", "rational", "cu doua zecimale exacte".
Fiind
data matricea :
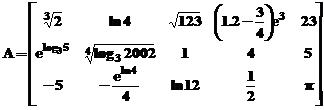
sa se determine (in MATLAB) matricea formata astfel:
A1-din elementele de pe pozitiile:
(1,5), (2,3), (2,5), (3,1), (3,3), (3,5), aranjate in toate variantele
posibile(2 linii / 3 coloane; 3 linii / 2 coloane; 1 linie / 6 coloane; 6 linii
/ 1 coloana);
A2-din elementele de pe liniile 1 si 3
coloanele 1, 3, 5;
A3-din elementele de pe "diagonalele
principale" cu 3 elemente;
A4-din elementele de pe "diagonalele
secundare" cu 2 elemente;
Se
da matricea (scrisa conform conventiilor MATLAB):
M=[1,2,3,4,5,6,7,8,9,10;-1,2,3,-4,5,-6,7,-8,9,-10;0,2,0,4,0,6,0,8,0,10;
se cere sa se determine (in MATLAB) matricile formate astfel:
- Elementele
liniilor 1, 2, 4 si coloanelor 3, 5, 10;
- Elementele tuturor
liniilor matricei M si
coloanele 1, 2, 3, 6, 8, 9,10;
- Elementele
liniilor 1, 2, 3, 5, 6 si coloanelor 1, 3, 5, 7, 9;
- Elementele
liniilor 1, 3, 6 si coloanelor 10, 3, 2, 1 (in aceasta ordine)
- Elementele
liniilor 6, 5, 4, 3, 2, 1 si coloanele 10, 9, 8, . , 2, 1 (in
aceasta ordine)
Sa
se calculeze valoarea expresiei E:
 , pentru x=
, pentru x=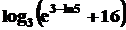 .
.


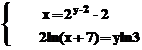 este realizabila
cu urmatoarea secventa:
este realizabila
cu urmatoarea secventa: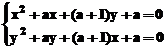 ;
; 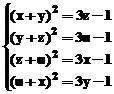 . Secventa urmatoare rezolva primul sistem:
. Secventa urmatoare rezolva primul sistem:
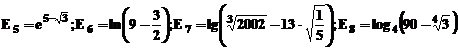
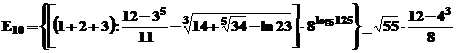
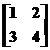 :
: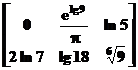 C=
C=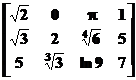
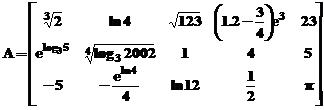
 , pentru x=
, pentru x=