 Descrierea tehnicii
Descrierea tehnicii
Aceasta tehnica se foloseste in rezolvarea problemelor care
indeplinesc simultan urmatoarele conditii:
- solutia lor poate fi pusa sub forma unui vector S=x1,x2,
,xn, cu x1 € A1, x2 € A2 ,,xn
€ An
- multimile A1, A2 , . ., An sunt
multimi finite, iar elementele lor se considera ca se afla
intr-o relatie de ordine bine stabilita;
- nu se dispune de o alta metoda de rezolvare, mai rapida
- x1 x2 . , xn pot fi la randul lor
vectori;
- A1, A2 . , An pot coincide.
Tehnica Backtracking are la
baza un principiu extrem de simplu:
- se construieste solutia pas cu pas: x1, x2
. ,xn
- daca se constata ca, pentru o valoare aleasa, nu avem
cum sa ajungem la solutie, se renunta la acea valoare
si se reia cautarea din punctul in care am ramas.
 Concret:
Concret:
- se alege primul element x1,
ce apartine lui A1;
- presupunand generate elementele x1,x2
. ,xk ,
apartinand multimilor A1,
A2 . ,Ak , se
alege (daca exista) xk+1 , primul element disponibil din
multimea Ak+1. Apar doua posibilitati :
1) Nu s-a gasit un astfel de element, caz in care caz in care se reia
cautarea considerand generate elementele x1,x2 . ,xk+1
, iar aceasta se reia de la urmatorul element al multimii Ak
ramas netestat;
2) A fost gasit, caz in care se testeaza daca acesta
indeplineste anumite conditii de continuare aparand astfel
doua posibilitati:
- indeplineste, caz in care
se testeaza daca s-a ajuns la solutie si apar din nou
doua posibilitati
- s-a ajuns la solutie, se
tipareste solutia si se reia algoritmul considerand
generate elementele x1,x2 . ,xk , (se cauta in
continuare, un alt element al multimii Ak , ramas netestat);
- nu s-a ajuns la solutie, caz
in care se reia algoritmul considerand generate elementele x1,x2
. ,xk , si se
cauta un prim element xk+2 € Ak.
- nu le indeplineste, caz in
care se reia algoritmul considerand generate elementele x1,x2
. ,xk , iar
elementul xk-1 se cauta intre elementele multimii A, ramase netestate.
Algoritmul se termina atunci cand nu exista nici un element x1
€ A1 netestat.
Observatie: tehnica Backtracking are ca
rezultat obtinerea tuturor solutiilor problemei. In cazul in care se
cere o sigura solutie se poate forta oprirea, atunci cand aceasta
a fost gasita.
Am aratat ca orice solutie se genereaza sub forma
de vector. Vom considera ca generarea solutiilor se face intr-o
stiva. Astfel, x1 € A1, se va gasi pe primul
nivel al stivei, x2 € A2 se va gasi pe al doilea
nivel al stivei,, xk € Ak se va gasi pe nivelul k
al stivei. In acest fel, stiva (notata ST) va arata astfel:

ST
Nivelul k+1 al stivei trebuie initializat (pentru a alege, in ordine,
elementele multimii k+1 ). Initializarea trebuie facuta cu
o valoare aflata (in relatia de ordine considerata, pentru
multimea Ak+1 ) inaintea tuturor valorilor posibile din
multime. De exemplu, pentru generarea permutarilor multimii
, orice nivel al stivei va lua valori de la 1 la n.
Initializarea unui nivel (oarecare) se face cu valoarea 0. Functia de
initializare o vom numi init().
Gasirea urmatorului element al multimii Ak
(element care a fost netestat) se face cu ajutorul functiei am_succesor(). Variabila as este o variabila booleana. In
situatia in care am gasit elementul, acesta este pus in stiva
si as ia valoarea TRUE, contrar
(nu a ramas un element netestat) as
ia valoarea FALSE.
Odata ales un element, trebuie vazut daca acesta
indeplineste conditiile de continuare (altfel spus, daca
elementul este valid). Acest test se face cu ajutorul functiei e_valid
Testul daca s-a ajuns sau nu la solutia finala se face cu
ajutorul functiei solutie(),
iar o solutie se tipareste cu ajutorul functiei tipar(). Prezentam in continuare
rutina back() descrisa in pseudocod:
Subalgoritm: BACK():
k
st[k]←0
cat timp k>0 executa
daca <mai
exista valori neincercate pe nivelul k> atunci
st[k] ←
<o noua valoare din multimea solutiilor posibile>
daca valid(k) returneaza 1 atunci
daca <solutia este finala> atunci
apel
tipar(k)
altfel
k← k+1; st[k] ←0
sfdaca
sfdaca
altfel
k ←k+1
sfdaca
Sfarsit cat timp
Sfarsit subalgoritm
Implementarea strategiei pentru problema permutarilor:
void back ()
}
else k--;
In cazul permutarilor, pentru ca o solutie sa fie
valida, valoarea pusa pe nivelul k trebuie sa nu se mai regaseasca pe nivelele
inferioare; acest lucru se testeaza cu urmatoarea functie valid(k):
int valid(int k)
Pentru a afisa o solutie finala apelam la functia tipar(k):
void tipar(int k)
Sarcini de lucru:
Se
citesc n si p. Sa se genereze toate aranjamentele de n luate cate p.
Care sunt asemanarile si deosebirile cu generarea permutarilor?
Se
citesc n si p. Sa se genereze toate combinarile de n luate cate p.
Care sunt asemanarile si deosebirile cu generarea aranjamentelor?
Fiind data o tabla de sah, de dimensiune n, xn,
se cere sa se scrie continutul funtiilor standard din rutina
back ce genereaza toate solutiile de aranjare a n dame, astfel incat
sa nu se afle doua dame pe aceeasi linie, coloana sau
diagonala (damele sa nu se atace ). Precizati ce punem pe
stiva si ce reprezinta nivelul stivei in acest caz, precum si functiile
programului.
Fiind
data o harta cu n tari, se cer
toate solutiile de colorare a hartii, utilizand cel mult 4
culori, astfel incat 2 tari cu frontiera comuna sa fie
colorate diferit. Este demonstrat matematic faptul ca sunt suficiente
numai 4 culori pentru ca orice harta sa poata fi colorata
astfel.
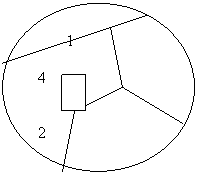
Pentru
exemplificare, vom considera harta de mai sus unde tarile sunt
numerotate cu cifre cuprinse intre 1
si 5:
O
solutie a acestei probleme este urmatoarea:
- Tara 1 – culoarea 1
- Tara 2 – culoarea 2
- Tara 3 – culoarea 1
- Tara 4 – culoarea 3
- Tara 5 – culoarea 4
 Harta este furnizata programului cu ajutorul unei
matrice (tablou)
Harta este furnizata programului cu ajutorul unei
matrice (tablou)  .
.
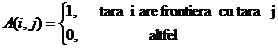
Matricea
A este simetrica. Pentru rezolvarea problemei se utilizeaza
stiva st , unde nivelul k al stivei
simbolizeaza tara k, iar st[k]
culoarea atasata tarii k. Stiva are inaltimea n
si pe fiecare nivel ia valori intre 1 si 4.
#include<iostream.h>
int st[10],a[20][20],n,k;
int e_valid()
void tipar()
void back ()
}
else k--;
main()
back();
Un
comis-voiajor trebuie sa viziteze un numar de n orase.
Initial, acesta se afla intr-unul
dintre
ele, notat 1. Comis-voiajorul doreste sa nu treaca de doua
ori prin acelasi oras,iar la intoarcere sa revina in orasul
1. Cunoscand legaturile existente intre orase, se cere sa se
tipareasca toate drumurile posibile pe care le poate efectua comis-voiajorul.
 In figura de mai jos sunt simbolizate, pentru n=6, cele 6
orase, precum si drumurile
existente intre ele.
In figura de mai jos sunt simbolizate, pentru n=6, cele 6
orase, precum si drumurile
existente intre ele.

Comis-voiajorul are urmatoarele
posibilitati de parcurgere:
Pentru metoda backtracking recursiv,
solutiile finale st[i] sunt generate in cadrul functiei back_recursiv(int k),
unde k reprezinta nivelul pana la care s-a ajuns pe stiva.
Adica la fiecare executie din lantul de auto apeluri, functia back recursiv trateaza nivelul k al stivei.
Algoritmul recursiv de backtracking este prezentat mai jos in
limbajul pseudocod.
back_recursiv( int k)
pentru contor de la <v1>
la <vn> executa
st[k]←contor
daca
valid(k) atunci
daca<solutia este finala> atunci
apel tipar
altfel auto-apel back_recursiv(k+1)
sfarsitdaca
sfarsitdaca
sfarsitpentru
Intr-un
ciclu, prin variabila contor vor trece pe rand toate valorile din intervalul <v1>
la <vn>
care ar putea fi incercate pe nivelul k al stivei. La fiecare pas al ciclului,
pentru fiecare dintre valorile variabilei contor:
.Se memoreaza pe nivelul k valoarea
contor prin st[k]←contor. Se obtine astfel solutia
partiala(st[1],st[2], . ,st[k]),
Se
verifica
daca aceasta solutie este valida prin functia valid(k).
Daca da atunci se verifica
daca solutia este finala :
Daca
este solutie finala atunci se apeleaza functia tipar;
In caz contrar, avem o solutie valida dar care nu este si
finala; vom urca la nivelul
urmator in stiva prin apelul back_recursiv(k+1).
Algoritmul se reia de la
capat,
dar cu k+1 in
loc de k.
Sarcini de lucru:
Problema damelor rezolvata recursiv
#include
<conio.h>
#include <iostream.h>
#define nmax 10
int n;
/*dimensiunea (ordinul) tablei de sah */
int nr_solutie;
int x[nmax];
int valid(int k)
void back_recursiv(int k)
;
getch();
}
}
}
void main()
 Sarcina de lucru: (PROIECT)
Sarcina de lucru: (PROIECT)
Sa
se realizeze un portofoliu de 5 probleme ce au ca algoritm de rezolvare metoda
backtracking recursiv, enunt, rezolvare, testare pentru date de intrare
corespunzatoare diferitelor cazuri. Codul sursa sa fie cu comentarii referitoare la semnificatia variabilelor si a functiilor
folosite.




