Tehnica de programare "Divide et Impera"

Divide et impera este o tehnica speciala prin care se pot rezolva anumite probleme.

Tehnica " Divide et Impera" consta in doua etape:

• Divide. Problema data este impartita in doua sau mai multe subprobleme de acelasi tip, dar de dimensiuni mai mici. Subproblemele se rezolva direct, daca dimensiunea lor permite aceasta (cazuri elementare), sau, fiind de acelasi tip, se rezolva in mod recursiv, prin acelasi procedeu.
• Impera. Se combina solutiile subproblemelor pentru a obtine solutia problemei initiale.

Restrictii

Metoda Divide Et Impera se poate aplica in rezolvarea unei probleme care indeplineste urmatoarele conditii:

se poate descompune in ( doua sau mai multe) subprobleme ;

aceste subprobleme sunt independente una fata de alta (o subproblema nu se rezolva pe baza alteia si nu se foloseste de rezultatele celeilalte);

aceste subprobleme sunt similare cu problema initiala;

la randul lor subproblemele se pot descompune (daca este necesar) in alte subprobleme mai simple;

aceste subprobleme simple se pot solutiona imediat prin algoritmul simplificat.

Numarul problemelor care se rezolva prin aceasta metoda este relativ mic, tocmai datorita restrictiilor de mai sus.

Schema generala

Metoda Divide Et Impera admite o implementare recursiva, deoarece subproblemele sunt similare problemei initiale, dar de dimensiuni mai mici.
Principiul fundamental al recursivitatii este autoapelarea unui subprogram cand acesta este activ; ceea ce se intampla la un nivel, se intampla la orice nivel, avand grija sa asiguram conditia de terminare a apelurilor repetate. Asemanator se intampla si in cazul metodei Divite Et Impera la un anumit nivel sunt doua posibilitati:

• s-a ajuns la o (sub)problema simpla ce admite o rezolvare imediata, caz in care se rezolva (sub)problema si se revine din apel (la subproblema anterioara, de dimensiuni mai mari);
• s-a ajuns la o (sub)problema care nu admite o rezolvare imediata, caz in care o descompunem in doua sau mai multe subprobleme si pentru fiecare din ele se continua apelurile recursive (ale procedurii sau functiei).

In etapa finala a metodei Divide Et Impera se produce combinarea subproblemelor (rezolvate deja) prin secventele de revenire din apelurile recursive.

Etapele metodei Divide Et Impera sunt:

Identificarea dimensiunii subproblemelor

In general un subprogram Divide Et Impera se aplica unui tablou (vector) V = <v₁,,v_n> (V[1..n], n=dim[V]), asupra caruia vrem sa aplicam o operatie oarecare (sortare, determinarea valorii maxime, determinarea cmmdc, etc).

Identificarea modalitatii de impartire in subprobleme

In acest caz se executa impartirea in doua subprobleme de dimensiuni aproximativ egale si anume [n/2] . Impartirea in subprobleme are loc pana cand dimensiunea acestora devine suficient de mica pentru a fi rezolvate in mod direct (cazul de baza).

Rezolvarea subproblemelor

Se rezolva subproblema directa.

Combinarea solutiilor

Dupa rezolvarea celor doua subprobleme se executa faza de combinare a rezultatelor in vederea rezolvarii intregii probleme. Se face prin interclasarea solutiilor.

Subprogramul divide

Subprogram DivImp(V,p,q)

  Daca q-p <= 1 atunci  Rezolva(V,p,q)

       altfel  m=(p+q) div 2

         DivImp(V,p,m)

         DivImp(V,m+1,q)

         Combina(V,p,m,q)

  Sf_Daca

Sf_subprogram.

Apelul subprogramului

Initial p=1, q=n, rezulta DivImp V,1,n).

Aplicatii practice

Maximul dintr-un vector

Se citeste un vector cu n componente, numere naturale. Se cere sa se tipareasca valoarea maxima din sir.

Descriere

Trebuie tiparita valoarea maxima dintre numerele retinute in vector de la i la j (initial i= 1, j=n). Pentru aceasta procedam astfel :

• daca i=j, valoarea maxima va fi v[i] ;
• contrar vom imparti vectorul in doi vectori (primul vector va contine componentele de la i la (i+j) div 2, al doilea va contine componentele de la ((i+j) div 2 +1 la j ) , rezolvam subproblemele (aflam maximul pentru fiecare din ele) iar solutia problemei va fi data de valoarea maxima dintre rezultatele celor doua subprobleme.

#include<iostream.h>

int v[10],n;

int max(int i ,int j)

}

main( )

cout<<"max="<<max(1,n);

}

Cautarea binara

Descriere

Daca elementele vectorului sunt ordonate crescator, putem sa ne dam seama daca elementul nu exista in vector fara a fi nevoie sa parcurgem toate elementele vectorului. Unul dintre algoritmii folositi in acest caz este algoritmul de cautare binara. Acest algoritm are la baza principiul injumatatirii repetate a domeniului in care se cauta elementul, prin impartirea vectorului in doi subvectori. Notam cu st primul indice al vectorului si cu dr ultimul indice al vectorului, iar m este indicele elementului din mijloc al vectorului m=(st+dr)/2. Se compara valoarea cautata cu valoarea elementului din mijloc. Daca cele doua valori sunt egale inseamna ca s-a gasit elementul. Daca nu sunt egale vectorul v-a fi impartit in doi subvectori. Operatia de cautare consta in identificarea subvectorului in care se poate gasi elementul, prin compararea valorii cautate cu cea din mijloc, dupa care se divizeaza acest subvector in doi subvectori s.a.m.d. pana cand se gaseste elementul, sau pana cand nu se mai poate face impartirea in subvectori, ceea ce inseamna ca nu s-a gasit elementul.

Exemplu: Dorim sa cautam elementul x=19 intr-un vector cu 9 elemente:

st=1 dr=9 m=5

elementul cautat este x=19

se cauta in subvectorul din dreapta st=m+1=6

19<20 se cauta in subvectorul din stanga dr=m-1=6

st=m=5

19>17 se cauta in subvectorul din dreapta st=m+1=6

st=dr=m=6 Elementul a fost gasit

Algoritm descris in pseudocod

Functia CautBin n,A,x)

p←1 q←n

cat timp p≤q executa

m ← [(p+q)/2]

daca x=A[m] atunci

CautBin ← m p ← q+1

altfel

daca x<A[m] atunci q ← m-1

altfel p ← m+1

sfdaca

sfdaca

sfcat timp sfCautBin

3.Sortarea prin interclasare - MergeSort

Descriere

Algoritmul de sortare prin interclasare se bazeaza pe urmatoarea idee: pentru a sorta un vector cu n elemente il impatim in doi vectori care, odata sortati, se interclaseaza.

Conform strategiei Divide et Impera, problema este descompusa in alte doua subprobleme de acelasi tip si, dupa rezolvarea lor, rezultatele se combina (in particular se interclaseaza). Descompunerea unui vector in alti doi vectori care urmeaza a fi sortati are loc pana cand avem de sortat vectori de una sau doua componente.

Exemplu Sortarea unui sir de sapte valori de tip intreg.

4. Sortarea rapida quicksort)

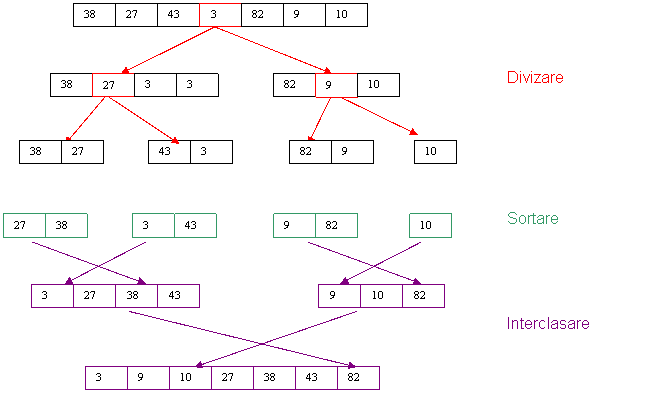
Descriere

Metoda divide et impera este utilizata in sortarea rapida. Mai jos este explicata varianta recursiva:

1. Se alege o valoare pivot. Se ia valoarea elementului din mijloc ca valoare pivot, dar poate fi oricare alta valoare, care este in intervalul valorilor sortate, chiar daca nu este prezenta in tablou.

2. Partitionare, Se rearanjeaza elementele in asa fel incat, toate elementele care sunt mai mari decat pivotul merg in partea dreapta a tabloului. Valorile egale cu pivotul pot sta in orice parte a tabloului. In plus, tabloul poate fi impartit in parti care nu au aceeasi dimensiune (nu sunt egale).

3. Se sorteaza amandoua partile.se aplica recursiv algoritmul de sortare rapida in partea stanga si in partea dreapta.

Algoritmul de partitie in detaliu.

Exista 2 indici i si j, si la inceputul algoritmului de partitionare i indica primul element al tabloului iar j indica ultimul element din tablou. La pasul urmator algoritmul muta i inainte, pana cand un element cu o valoare mai mare sau egala cu pivotul este gasita. Indicele j este mutat inapoi, pana cand un element cu valoare mai mica sau egala cu pivotul este gasita. Daca i<=j atunci i merge pe pozitia i+1 iar j merge pe pozitia j-1. Algoritmul se opreste, cand i devine mai mare decat j.

Exemplu: dorim sa sortam sirul folosind sortarea rapida.
- nesortat
, 13, 7, 28, , 16, 3, 10, - valoarea pivot = 10
1, , 7, 28, , 16, 3, 10, - 13 >= 10 >= 2, interschimbam 13 cu 2
1, 2, 7, , 16, 3, , 13 - 28 >= 10 >= 10 , interschimbam 28 cu 10
1, 2, 7, , , 16, , 28, 13 - 10 >= 10 >= 3, interschimbam 10 cu 3
1, 2, 7, 10, 3, 16, 10, 28, 13 - i > j, se opreste partitionarea
se aplica din nou algoritmul pentru 1, 2, 7, 10, 3 si 16, 10, 28, 13
Se obtine: - sir sortat

Algoritm descris in pseudocod:

QuickSort(V,st,dr);

pivot←v[(st+dr) div 2)];

cat timp i<=j executa

cat timp v[i] <pivot executa i←i+1;

sfcat timp

cat timp v[j] >pivot executa j←j-1;

sfcat timp

daca i<=j atunci

aux←v[i];v[i]←v[j];v[j]←aux;i←i+1;j←j-1;

sfdaca

sfcat timp

daca st<j atunci quikSort(v,st,j);

sfdaca

daca i<dr atunci quikSort(v,i,dr);

sfdaca

sfQuickSort