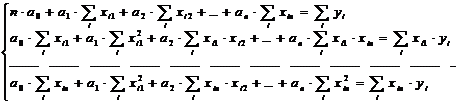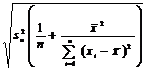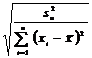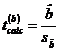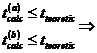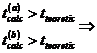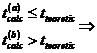Regresia
si corelatia statistica in cercetarea de marketing
Cercetarea
cantitativa de piata ofera o gama mare de metode
pentru studiul dependentei dintre doua sau mai multe variabile.
Aceste metode studiaza dependenta dintre o variabila
rezultativa, notat cu  si una sau
mai multe variabile factoriale, notate in general cu
si una sau
mai multe variabile factoriale, notate in general cu 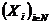 .De exemplu, volumul vanzarilor unui produs
.De exemplu, volumul vanzarilor unui produs  intr-o
perioada data este
influentat de nivelul cheltuielilor publicitare
intr-o
perioada data este
influentat de nivelul cheltuielilor publicitare  , atunci exprimarea dependentei vanzarilor de
cheltuielile publicitare printr-o relatie de forma:
, atunci exprimarea dependentei vanzarilor de
cheltuielile publicitare printr-o relatie de forma:  . Daca avem in vedere si alte variabile in studiul
volumului vanzarilor cum ar fi:
pretul
. Daca avem in vedere si alte variabile in studiul
volumului vanzarilor cum ar fi:
pretul 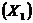 si venitul mediu
al consumatorilor
si venitul mediu
al consumatorilor  acest fapt ar putea fi
exprimat in limbaj matematic printr-o relatie de forma:
acest fapt ar putea fi
exprimat in limbaj matematic printr-o relatie de forma:
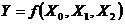 ,in care
,in care 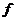 este o functie de
trei variabile.
este o functie de
trei variabile.
Daca s-ar putea identifica functia 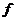 atunci s-ar putea
prezice volumul vanzarilor in anumite conditii in ipoteza in care ar
fi cunoscute cheltuielile publicitare, pretul si venitul mediu al
consumatorilor. Aceste legaturi pot fi puse in evidenta numai
daca exista un mare numar de cazuri individuale (legea numerelor
mari). In acest fel, legaturile dintre variabile apar ca legaturi statistice sau
stohastice. O categorie aparte de
metode sunt cele parametrice sau de analiza a legaturii dintre
variabile. Metoda regresiei constituie o metoda statistica de
cercetare a legaturii dintre variabile cu ajutorul unor functii
matematice, denumite functii de regresie. Prin functie de regresie se intelege o expresie
matematica, dedusa in urma prelucrarii unor date experimentale,
ce aproximeaza (estimeaza) dependentele dintre doua sau mai
multe variabile ale unui sistem sau proces. Determinarea unei functii de
regresie este necesara atunci cand dependentele dintre variabilele
respective nu pot fi stabilite suficient de precis pe cale teoretica. Estimarea unui model matematic al
tendintei legaturii dintre presupune parcurgerea urmatoarelor etape:
atunci s-ar putea
prezice volumul vanzarilor in anumite conditii in ipoteza in care ar
fi cunoscute cheltuielile publicitare, pretul si venitul mediu al
consumatorilor. Aceste legaturi pot fi puse in evidenta numai
daca exista un mare numar de cazuri individuale (legea numerelor
mari). In acest fel, legaturile dintre variabile apar ca legaturi statistice sau
stohastice. O categorie aparte de
metode sunt cele parametrice sau de analiza a legaturii dintre
variabile. Metoda regresiei constituie o metoda statistica de
cercetare a legaturii dintre variabile cu ajutorul unor functii
matematice, denumite functii de regresie. Prin functie de regresie se intelege o expresie
matematica, dedusa in urma prelucrarii unor date experimentale,
ce aproximeaza (estimeaza) dependentele dintre doua sau mai
multe variabile ale unui sistem sau proces. Determinarea unei functii de
regresie este necesara atunci cand dependentele dintre variabilele
respective nu pot fi stabilite suficient de precis pe cale teoretica. Estimarea unui model matematic al
tendintei legaturii dintre presupune parcurgerea urmatoarelor etape:
|
intuirea
unor relatii matematice a modelelor pe baza reprezentarii grafice a
corelatiei;
estimarea
parametrilor pentru fiecare model in parte, cel mai adesea cu ajutorul metodei
celor mai mici patrate (MCMMP);
alegerea
modelului care reda cel mai fidel relatia evidentiata de
date (criteriul de minim al MCMMP);
testarea
semnificatiei modelului ales si a coeficientilor
functiilor gasite;
interpretarea
economica a parametrilor testati;
utilizarea
modelului pentru simulare si prognoze.
|
Dupa
numarul factorilor de influenta ai caracteristicii rezultative
exista:
- regresia unifactoriala sau simpla;
- regresia multifactoriala sau
multipla.
Regresia unifactoriala are in
vedere cuantificarea relatiilor de
dependenta sub forma unor modele unifactoriale, verificarea
ipotezelor si fundamentarea calculelor de prognoza.
Modelele unifactoriale descriu
legatura dintre doua variabile  si
si 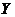 , ceilalti factori considerandu-se cu actiune
constanta. Ecuatia teoretica a acestei regresii este de forma :
, ceilalti factori considerandu-se cu actiune
constanta. Ecuatia teoretica a acestei regresii este de forma :  , unde
, unde 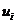 reprezinta
actiunea altor factori (perturbatia), iar
reprezinta
actiunea altor factori (perturbatia), iar 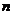 numarul
observatiilor. Estimarea
parametrilor acestui model se realizeaza cu ajutorul metodei celor mai mici patrate (MCMMP), care presupune
minimizarea sumei patratelor abaterilor valorilor empirice (
numarul
observatiilor. Estimarea
parametrilor acestui model se realizeaza cu ajutorul metodei celor mai mici patrate (MCMMP), care presupune
minimizarea sumei patratelor abaterilor valorilor empirice ( ) de la valorile estimate (
) de la valorile estimate ( ):
): 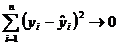 .
.
In practica cercetarii de piata cele mai
utilizate modele sunt:
- modelul liniar:
 ;
;
- modelul exponential:
 ;
;
- modelul putere:
 ;
;
- modelul parabolic:
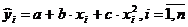 ;
;
- modelul hiperbolic:
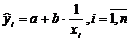 ;
;
- modelul logistic:
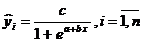
Calculul si interpretarea parametrilor
modelului liniar. In
modelele liniare unifactoriale, variabila rezultativa 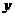 depinde de un singur
factor
depinde de un singur
factor 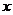 prin relatia :
prin relatia :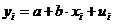 ,
, 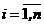 unde
unde 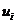 reprezinta
actiunea altor factori decat factorul analizat (perturbatia), iar
reprezinta
actiunea altor factori decat factorul analizat (perturbatia), iar 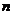 numarul
observatiilor.
numarul
observatiilor.
Estimarea parametrilor acestui model
se poate realiza tot cu ajutorul metodei
celor mai mici patrate (MCMMP), care presupune minimizarea sumei
patratelor abaterilor valorilor empirice ( ) de la valorile estimate (
) de la valorile estimate ( ):
):  , unde
, unde 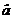 si
si  sunt estimatorii
parametrilor modelului liniar.Minimizarea sumei presupune determinarea
punctelor stationare care rezulta din rezolvarea sistemului
obtinut prin anularea derivatelor partiale ale functiei:
sunt estimatorii
parametrilor modelului liniar.Minimizarea sumei presupune determinarea
punctelor stationare care rezulta din rezolvarea sistemului
obtinut prin anularea derivatelor partiale ale functiei: 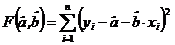 se ajunge la
urmatorul sistem de ecuatii:
se ajunge la
urmatorul sistem de ecuatii:
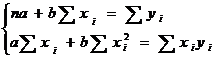 ,iar dupa efectuarea calculelor se obtin
urmatoarele relatii de determinare a estimatorilor:
,iar dupa efectuarea calculelor se obtin
urmatoarele relatii de determinare a estimatorilor:
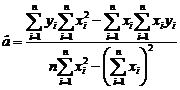
 .
.
In acelasi mod se
procedeaza si in cazul altor modele decat cel liniar. Inainte de-a
testa semnificatia estimatorilor si respectiv pentru a valida
modelul, este necesar ca in cazul in care se considera ca
tendinta legaturii poate fi estimata cu mai multe modele,
sa se aleaga acel model care indeplineste conditia de minim
si anume: 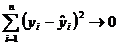 .
.
Un intreprinzator doreste sa
cumpere un spatiu comercial de aproximativ 30 de mp intr-o zona
comerciala. In acest sens, doreste sa afle estimativ cifra de
afaceri pe care o poate obtine in aceasta situatie. Studiile
realizate in zona comerciala arata ca cifra de afaceri a
magazinelor cu profilul respectiv depinde de suprafata comerciala.
Informatiile referitoare la acesti indicatori, inregistrate la 10
magazine avand acelasi profil:
|
Suprafata comerciala, mp
|
|
|
|
|
|
|
|
|
|
|
|
Cifra de afaceri, mii euro
|
|
|
|
|
|
|
|
|
|
|
Intre aceste doua variabile exista o
relatie cauzala, in sensul ca cifra de afaceri anuala poate
deveni o functie a suprafetei comerciale. Deci, cifra de afaceri
anuala reprezinta variabila dependenta 'y', iar
suprafata comerciala reprezinta variabila independenta
'x'.
Principala
metoda simpla de identificare a legaturii dintre variabile este
metoda grafica. Verificarea
semnificatiei economice dintre cele doua variabile se realizeaza
prin corelograma construita in sistemul de axe ortogonale unde pe
abscisa se reprezinta suprafata comerciala, iar pe
ordonata cifra de afaceri anuala. Din graficul nr.1 se poate observa
ca punctele sunt concentrate pe principala bisectoare, identificand o
legatura directa intre cele doua variabile.
Evolutia
legaturii dintre suprafata comerciala si cifra de afaceri anuala
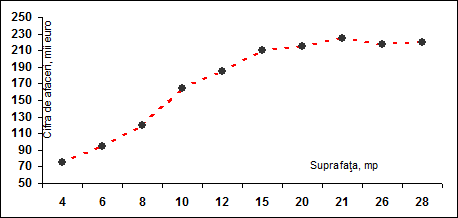
Pentru
exprimarea tendintei generale a legaturii dintre cele doua
variabile vom utiliza urmatoarele modele
ipotetice, sugerate de reprezentarea grafica:
modelul
liniar: 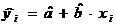 ;
;
modelul
exponential: 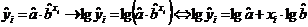
Pentru
estimarea parametrilor modelelor ipotetice propuse se utilizeaza MCMMP,
obtinandu-se pentru fiecare model in parte sistemul de ecuatii
aferent:
modelul
liniar: 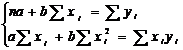 ;
;
modelul
exponential: 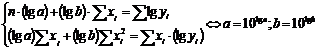 .
.
Pe baza
datelor din tabelul *.2. valoarea parametrilor este:
modelul
liniar: 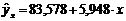 ;
;
modelul
exponential: 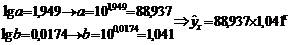 ;
;
Valorile ajustate ale
cifrei de faceri in functie de suprafata comerciala
|
Suprafata
comerciala
|
Cifra de
afaceri anuala
|
Ajustare dupa
functia
|

|
|
Exponentiala
|
Liniara
|
Exponentiala
|
Liniara
|
|
A
|
B
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Modelul
care indeplineste criteriul de minim al MCMMP este modelul liniar conform
tabelului nr.2 (totalul coloanelor 3 si 4). In cazul in care
intreprinzatorul doreste sa cumpere un magazin cu suprafata
de 30 mp, cifra de afaceri anuala estimata este de:
 mii euro
mii euro
Coeficientul
"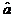 " poate lua atat valori pozitive cat si valori negative si
reprezinta ordonata la origine, respectiv, este valoarea lui "
" poate lua atat valori pozitive cat si valori negative si
reprezinta ordonata la origine, respectiv, este valoarea lui "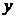 " cand "
" cand "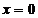 ".
".

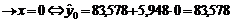 mii euro.
mii euro.
Coeficientul
"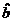 " este cunoscut sub denumirea de coeficient de regresie.
Acesta arata cu cat se modifica in medie variabila rezultativa
atunci cand variabila factoriala se modifica cu o unitate. In
functie de semnul coeficientului de regresie se poate aprecia tipul de
legatura:
" este cunoscut sub denumirea de coeficient de regresie.
Acesta arata cu cat se modifica in medie variabila rezultativa
atunci cand variabila factoriala se modifica cu o unitate. In
functie de semnul coeficientului de regresie se poate aprecia tipul de
legatura:
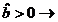 legatura
dintre variabile este una directa;
legatura
dintre variabile este una directa; intre cele
doua variabile nu exista legatura;
intre cele
doua variabile nu exista legatura;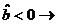 legatura
dintre variabile este una inversa.
legatura
dintre variabile este una inversa.
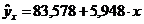
 legatura dintre
cele doua variabile este una directa. De asemenea, la o crestere
a suprafetei cu 1 mp, cifra de afaceri crestere in medie cu 5.948 mii
euro.
legatura dintre
cele doua variabile este una directa. De asemenea, la o crestere
a suprafetei cu 1 mp, cifra de afaceri crestere in medie cu 5.948 mii
euro.
In cazul fenomenelor de piata, o variabila
rezultativa  se defineste in
functie de mai multe variabile factoriale ceea ce implica
utilizarea regresiei multifactoriale:
se defineste in
functie de mai multe variabile factoriale ceea ce implica
utilizarea regresiei multifactoriale:
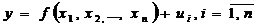 unde
unde 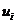 reprezinta actiunea altor factori
(perturbatia), iar
reprezinta actiunea altor factori
(perturbatia), iar 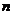 numarul
observatiilor. Daca legatura dintre fiecare factor si
variabila rezultativa este liniara, atunci functia de regresie
devine:
numarul
observatiilor. Daca legatura dintre fiecare factor si
variabila rezultativa este liniara, atunci functia de regresie
devine: 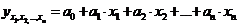 ,in care:
,in care:
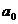 - parametrul
care concentreaza influenta factorilor neinregistrati,
considerati cu actiune constanta;
- parametrul
care concentreaza influenta factorilor neinregistrati,
considerati cu actiune constanta; - variabilele factoriale incluse in raportul de
cercetare;
- variabilele factoriale incluse in raportul de
cercetare; -coeficientii de
regresie, care arata cu cat se modifica variabila
rezultativa atunci cand variabila factoriala se modifica cu o unitate.
-coeficientii de
regresie, care arata cu cat se modifica variabila
rezultativa atunci cand variabila factoriala se modifica cu o unitate.
Estimarea
parametrilor acestui model se poate realiza cu ajutorul metodei celor mai mici patrate (MCMMP), care presupune
minimizarea sumei patratelor abaterilor valorilor empirice ( ) de la valorile estimate (
) de la valorile estimate ( ):
):
 ,
,
unde  sunt estimatorii
parametrilor modelului liniar.
sunt estimatorii
parametrilor modelului liniar.
Minimizarea
sumei presupune determinarea punctelor stationare care rezulta din
rezolvarea sistemului obtinut prin anularea derivatelor partiale ale
functiei:

Pe baza datelor empirice se construieste urmatorul sistem de
ecuatii:
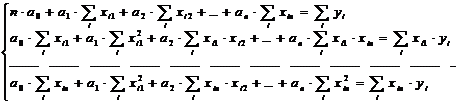
Pe baza elementelor teoretice prezentate, trebuie sa ne
pronuntam asupra semnificatiei statistice a parametrilor
de regresie, precum si asupra validitatii modelului
adoptat. In continuare, vom nota cu  si
si  , mediile variabilelor
, mediile variabilelor 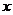 , respectiv
, respectiv 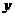 .Verificarea semnificatiei estimatorilor consta in a
accepta sau a respinge una dintre ipotezele:
.Verificarea semnificatiei estimatorilor consta in a
accepta sau a respinge una dintre ipotezele:
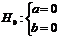
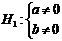
Testul adecvat acestui scop este testul "t", care presupune determinarea lui 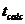 pentru fiecare dintre
parametrii
pentru fiecare dintre
parametrii 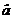 ,
,  .
.
Tabel nr. 4
|
Indicatori
|
Formula de calcul
|

|
|
A
|
|
|
|
Dispersia variabilei reziduale
|

|
|
|
Abaterea standard a estimatorului
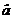 - - 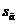
|
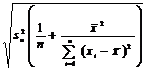
|
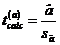
|
|
Abaterea standard a estimatorului
 - - 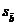
|
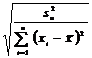
|
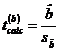
|
Aceste valori (coloana 2
din tabel) se compara cu valorile teoretice ale repartitiei Student  , corespunzatoare unui prag de semnificatie
, corespunzatoare unui prag de semnificatie 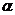 si numarului
gradelor de libertate
si numarului
gradelor de libertate  ,
, 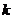 fiind numarul
variabilelor exogene.
fiind numarul
variabilelor exogene.
Pe aceasta baza, regula de decizie a
testului este urmatoarea:
|
daca 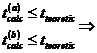
|
Se accepta 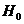 , ceea ce inseamna ca estimatorii parametrilor nu sunt
semnificativ diferiti de zero si se renunta la modelul specificat; , ceea ce inseamna ca estimatorii parametrilor nu sunt
semnificativ diferiti de zero si se renunta la modelul specificat;
|
|
daca 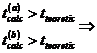
|
Se accepta 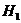 , ceea ce inseamna ca modelul
a fost corect specificat, identificat si estimat; , ceea ce inseamna ca modelul
a fost corect specificat, identificat si estimat;
|
|
daca 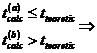
|
Se retine
modelul.
|
Stiind ca estimatorii sunt repartizati
normal, putem estima intervalul de
incredere al parametrilor:

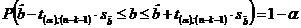
Daca coeficientii de regresie ai
modelelor estimate apartin unor intervale de incredere care contin
si valoarea 0, se renunta la model
Dupa verificarea
semnificatiei parametrilor, urmeaza etapa de validare a modelului specificat din punct de vedere statistic. In acest sens,
se utilizeaza testul Snedecor-Fisher.
Aplicarea acestui test presupune calculul
indicatorilor prezentati sintetic in continuare:
Tabel
nr. 5
|
Sursa de variatie
|
Masura
variatiei
|
Numarul gradelor de libertate
|
Dispersii corectate
|
Valoarea testului "F"
|
|
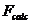
|

|
|
A
|
|
|
|
|
|
|
Variatia explicata
de model
|
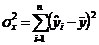
|
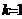
|

|

|
Valoarea
teoretica a testului "F"
|
|
Variatia
reziduala
|
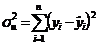
|
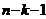
|
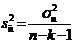
|
|
|
Variatia
totala
|
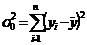
|
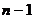
|
|
|
Pe baza datelor din tabel se pot testa urmatoarele ipoteze:
|
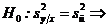
|
Cele
doua dispersii sunt aproximativ egale, altfel spus influenta
factorului 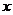 nu difera de
influenta factorilor intamplatori; nu difera de
influenta factorilor intamplatori;
|
|

|
Cele doua dispersii sunt diferite, adica influenta
factorului 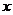 este
semnificativa. este
semnificativa.
|
Raportul dintre 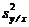 si
si 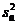 reprezinta
valoarea calculata "F" (coloana 4 din tabel), care se
compara cu cea tabelata
reprezinta
valoarea calculata "F" (coloana 4 din tabel), care se
compara cu cea tabelata  corespunzatoare nivelului de
semnificatie
corespunzatoare nivelului de
semnificatie 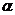 si numarului
gradelor de libertate
si numarului
gradelor de libertate 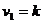 ,
,  .
.
Sunt posibile
situatiile urmatoare:
|
- daca  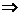
|
Se
accepta 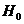 , ceea ce inseamna ca modelul
specificat nu este validat; , ceea ce inseamna ca modelul
specificat nu este validat;
|
|
- daca 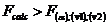 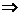
|
Se accepta 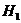 , ceea ce inseamna ca modelul este valid; , ceea ce inseamna ca modelul este valid;
|
|
Odata
validat modelul acesta poate fi utilizat in simulare sau prognoze
|


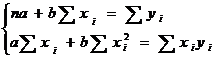 ,iar dupa efectuarea calculelor se obtin
urmatoarele relatii de determinare a estimatorilor:
,iar dupa efectuarea calculelor se obtin
urmatoarele relatii de determinare a estimatorilor: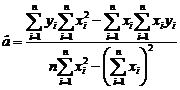
 .
.
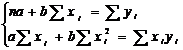 ;
;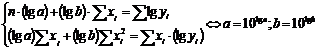 .
.