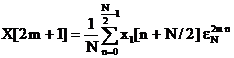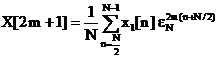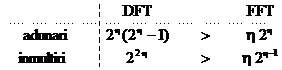Algoritmul FFT
Se foloseste des termenul FFT = Fast
Fourier Transform (Transformata Fourier Rapida). De fapt, este vorba
despre un algoritm care foloseste proprietatile functiilor
periodice pentru reducerea numarului de operatii aritmetice
si nu este o transformata cu proprietati matematice
diferite de cele ale transformatei DFT (Transformata Fourier Discreta).
Acest capitol reprezinta forma
matriceala a transformatei Fourier discrete, o demonstratie a
algoritmului FFT si modul in care sunt organizate datele si calculele
intr-un program care implementeaza algoritmul FFT.
Forma
matriceala a transformatei Fourier discrete
Primii pasi in scrierea unui program care
implementeaza transformata Fourier discreta sunt organizarea datelor
sub forma matriceala si gasirea unei metode eficiente
pentru calculul exponentialelor complexe.
Transformata DFT directa
Fie 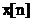 ,
, 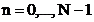 o secventa
prelevata din semnalul
o secventa
prelevata din semnalul
 , (3.1)
, (3.1)
prin esantionarea cu perioada T.
Transformata Fourier discreta transforma un semnal esantionat 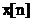 ,
, 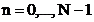 intr-un spectru
esantionat
intr-un spectru
esantionat 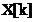 ,
, 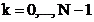
 . (3.2)
. (3.2)
Daca se noteaza:
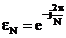 , (3.3)
, (3.3)
unde  se numeste
nucleul transformatei Fourier discrete de dimensiune N. Cu notatia (3.3)
esantioanele spectrului complex dat de transformata Fourier discreta
sunt:
se numeste
nucleul transformatei Fourier discrete de dimensiune N. Cu notatia (3.3)
esantioanele spectrului complex dat de transformata Fourier discreta
sunt:
 . (3.4)
. (3.4)
Daca se scrie functia (3.4) pentru 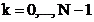 este indexul pentru
linii iar n este indexul pentru coloane, se obtine forma matriceala
a transformatei Fourier discrete
este indexul pentru
linii iar n este indexul pentru coloane, se obtine forma matriceala
a transformatei Fourier discrete
 , (3.5)
, (3.5)
Pentru ca 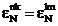 matricea transformatei
Fourier discrete este simetrica fata de diagonala
principala. Functia vectoriala (3.5) se poate pune si sub
forma:
matricea transformatei
Fourier discrete este simetrica fata de diagonala
principala. Functia vectoriala (3.5) se poate pune si sub
forma:
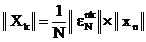 , (3.6)
, (3.6)
unde  este vectorul
esantioanelor semnalului analizat,
este vectorul
esantioanelor semnalului analizat,  este vectorul
esantioanelor spectrului esantionat dat de transformata Fourier
discreta iar matricea patrata
este vectorul
esantioanelor spectrului esantionat dat de transformata Fourier
discreta iar matricea patrata  ,
, 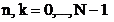 se numeste
matricea transformatei DFT de dimensiune N.
se numeste
matricea transformatei DFT de dimensiune N.
Calculul exponentialelor 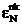
De exemplu pentru  transformata DFT sub
forma matriceala este :
transformata DFT sub
forma matriceala este :
 . (3.7)
. (3.7)
In cazul primei linii a matricei transformatei
DFT k = 0 si 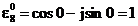 . Prin inmultirea primei linii a matricei cu vectorul
. Prin inmultirea primei linii a matricei cu vectorul 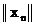 se obtine
se obtine 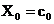 , care este valoarea medie a semnalului analizat.
, care este valoarea medie a semnalului analizat.

Figura
3.1 Calculul exponentialelor 
In figura 3.1 se prezinta cercul
trigonometric si exponentialele  ,
, 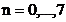 , care divizeaza cercul trigonometric in 8 puncte
echidistante. Exponentialele se calculeaza la inceputul programului
si se memoreaza intr-un vector de numere complexe
, care divizeaza cercul trigonometric in 8 puncte
echidistante. Exponentialele se calculeaza la inceputul programului
si se memoreaza intr-un vector de numere complexe
 . (3.8)
. (3.8)
In cazul celei de-a doua linii a matricei k =
1 si cercul din figura 3.1 este parcurs o singura data. Prin
inmultirea celei de-a doua linii a matricei transformatei cu vectorul 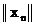 se obtine
se obtine  , corespunzator frecventei fundamentale a
transformatei Fourier discrete
, corespunzator frecventei fundamentale a
transformatei Fourier discrete  definita in
sectiunea 2.2.3.
definita in
sectiunea 2.2.3.
In cazul celei de-a treia linii k = 2, cercul
din figura 3.1 este parcurs de doua ori, deci se calculeaza
coeficientul Fourier c2 corespunzator frecventei  , armonica a doua a frecventei fundamentale a
transformatei Fourier discrete. Exponentialele se iau tot din vectorul
(3.8) pentru ca
, armonica a doua a frecventei fundamentale a
transformatei Fourier discrete. Exponentialele se iau tot din vectorul
(3.8) pentru ca
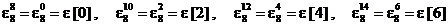 . (3.9)
. (3.9)
Calculul celorlalti coeficienti
Fourier nu mai are importanta pentru ca 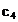 nu are semnificatie
fizica
nu are semnificatie
fizica 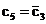 ,
, 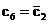 ,
,  (v. sectiunea
3.2.4).
(v. sectiunea
3.2.4).
In cazul general, exponentialele 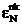 se iau dintr‑un
vector construit asemanator cu vectorul (3.8) folosind regula de
indexare
se iau dintr‑un
vector construit asemanator cu vectorul (3.8) folosind regula de
indexare
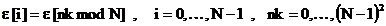 . (3.10)
. (3.10)
Transformata DFT inversa
Daca se cunoaste spectrul
esantionat al unui semnal, un esantion al semnalului original se
calculeaza cu formula:
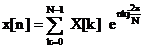 , (3.11)
, (3.11)
care este forma discreta a formulei
(2.3). Similar ca in sectiunea 3.1.1 se noteaza:
 (3.12)
(3.12)
si se obtine
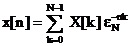 , (3.13)
, (3.13)
din care rezulta forma matriceala a
transformatei Fourier inverse :
 , (3.14)
, (3.14)
unde 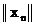 si
si  au aceeasi
semnificatie ca (3.6), iar
au aceeasi
semnificatie ca (3.6), iar  este matricea
transformatei Fourier discreta inversa.
este matricea
transformatei Fourier discreta inversa.
Fie o functie armonica cu perioada
principala  (v. definitiile
din sectiunea 2.1.1).
(v. definitiile
din sectiunea 2.1.1).
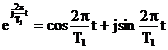 . (3.15)
. (3.15)
Armonicele acestei functii au
urmatoarea proprietate
 . (3.16)
. (3.16)
Demonstratia este imediata: pentru 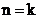 ,
,  , iar pentru
, iar pentru  , integrala
calculata pe un numar intreg de perioade dintr-o functie
armonica este nula. Daca exponentialele complexe (3.16) sunt
esantionate in N puncte si daca se folosesc notatiile (3.3)
si (3.12) rezulta
, integrala
calculata pe un numar intreg de perioade dintr-o functie
armonica este nula. Daca exponentialele complexe (3.16) sunt
esantionate in N puncte si daca se folosesc notatiile (3.3)
si (3.12) rezulta
 . (3.17)
. (3.17)
Demonstratia este similara. Pentru 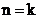 ,
,  deci suma da
valoarea 1. Cercul din figura 3.1 este divizat uniform in N puncte simetrice
fata de axa reala.
deci suma da
valoarea 1. Cercul din figura 3.1 este divizat uniform in N puncte simetrice
fata de axa reala.
Pentru  ,
, 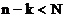 sunt parcurse toate
cele N puncte iar cercul este parcurs de
sunt parcurse toate
cele N puncte iar cercul este parcurs de 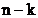 ori folosind regula de
indexare (3.10). In consecinta, partea imaginara a sumei (3.17)
este nula pentru ca se aduna partile imaginare ale
unor puncte simetrice fata de axa reala.
ori folosind regula de
indexare (3.10). In consecinta, partea imaginara a sumei (3.17)
este nula pentru ca se aduna partile imaginare ale
unor puncte simetrice fata de axa reala.
Daca N este par atunci punctele de pe
cerc sunt simetrice si fata de axa imaginara. In
consecinta si partea reala a sumei (3.17) este nula.
Proprietatea (3.17) poate fi demonstrata si pentru N impar, dar
demonstratia este laborioasa si rezultatul nu are
importanta practica. De exemplu, pentru  suma (3.17) da
suma (3.17) da
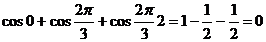 . (3.18)
. (3.18)
Utilizand (3.17), din (3.6) si (3.14)
rezulta ca
 . (3.19)
. (3.19)
Algoritmul
FFT
Transformata Fourier rapida (sau
algoritmul FFT) este o metoda de calcul pentru o transformata DFT
cu 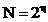 , esantioane ale semnalului
, esantioane ale semnalului 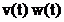 , din care se obtin
, din care se obtin 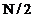 esantioane
independente ale spectrului esantionat. Numarul natural
esantioane
independente ale spectrului esantionat. Numarul natural 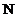 se numeste
dimensiunea transformatei FFT, iar numarul
se numeste
dimensiunea transformatei FFT, iar numarul 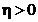 este numarul de
iteratii necesare in algoritmul FFT.
este numarul de
iteratii necesare in algoritmul FFT.
Principiul algoritmului FFT
In sens matematic, algoritmul este o
metoda sistematica de rezolvare a unei categorii de probleme. In sens
informatic, algoritmul este un set de instructiuni prestabilit prin care
se rezolva o anumita problema intr‑un numar finit de
pasi.
Algoritmul FFT are h iteratii,  . In continuare se prezinta o varianta a algoritmului
FFT in care se parcurg urmatorii pasi:
. In continuare se prezinta o varianta a algoritmului
FFT in care se parcurg urmatorii pasi:
iteratia 0 se aplica vectorului de
numere complexe 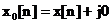 de dimensiune
de dimensiune 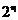 , indexat dupa regula,
, indexat dupa regula, 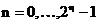 , din care se obtin doua transformate Fourier
rapide de dimensiune
, din care se obtin doua transformate Fourier
rapide de dimensiune  . Aceste rezultate intermediare sunt depuse in vectorul
. Aceste rezultate intermediare sunt depuse in vectorul 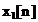 ;
;
iteratia 1 a algoritmului se aplica
separat celor doua jumatati ale vectorului 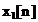 , indexate dupa regulile
, indexate dupa regulile  si respectiv
si respectiv  din care se obtin patru transformate Fourier
discrete de dimensiune
din care se obtin patru transformate Fourier
discrete de dimensiune  ;
;
algoritmul se incheie cu iteratia  , care se aplica celor 2h transformate Fourier Rapide de dimensiune
, care se aplica celor 2h transformate Fourier Rapide de dimensiune
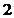 din vectorul
din vectorul  din care se obtin
din care se obtin
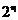 esantioane de
frecventa de forma
esantioane de
frecventa de forma  .
.
Observatie:
in iteratiile  , vectorii de numere complexe
, vectorii de numere complexe  nu au semnificatie
fizica si din acest motiv, vor fi numiti "vectorii variabilelor
intermediare" ;
nu au semnificatie
fizica si din acest motiv, vor fi numiti "vectorii variabilelor
intermediare" ;
Demonstratia algoritmului este in stil
constructivist. In principiu, daca se demonstreaza ca fiecare
iteratie se dubleaza numarul de transformate Fourier rapide
si se injumatateste dimensiunea lor si
daca se stabileste semnificatia fizica a numerelor complexe
din vectorul  , atunci algoritmul este demonstrat.
, atunci algoritmul este demonstrat.
Demonstratia algoritmului FFT
Se porneste de la formula transformatei
Fourier discrete (3.4) pusa sub forma
 , (3.20)
, (3.20)
unde indicii zero din 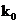 si
si 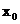 indica
numarul iteratiei curente, iar
indica
numarul iteratiei curente, iar  este indexul sumei din
iteratia curenta. La fiecare iteratie numerele complexe din
vectorul
este indexul sumei din
iteratia curenta. La fiecare iteratie numerele complexe din
vectorul 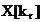 ,
, 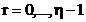 , isi schimba pozitiile datorita metodei
de calcul prezentata in continuare.
, isi schimba pozitiile datorita metodei
de calcul prezentata in continuare.
Se divizeaza secventa  in doua
jumatati
in doua
jumatati
 . (3.21)
. (3.21)
In a doua suma se face substitutia 
 , (3.22)
, (3.22)
unde se tine seama ca formula (2.20)
a fost dedusa in cazul primei ipoteze din sectiunea 2.2.2, deci in
cazul indexului si a limitei de indexare calculele se fac intr-o
clasa de resturi modulo 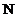
 . (3.23)
. (3.23)
Dupa ce se desface paranteza de la
exponentul celei de-a doua sume din (3.22) si se regrupeaza termenii
asemenea se obtine
 , (3.24)
, (3.24)
unde 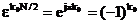 .
.
Se considera separat cazurile k par si k impar. Se noteaza  si se obtine
si se obtine
 ,
,  (3.25)
(3.25)
iar pentru k impar se noteaza 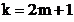 si se obtine
si se obtine
 ,
, 
 . (3.26)
. (3.26)
Se observa ca paranteza rotunda
din (3.25) si paranteza patrata din (3.26) sunt niste numere
complexe usor de evaluat. Se fac notatiile:
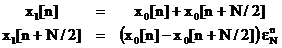 ,
, 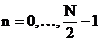 . (3.27)
. (3.27)
cu notatiile (3.27) se obtin
doua transformate Fourier rapide de dimensiune 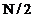 :
:
 , (3.28)
, (3.28)
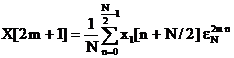 , (3.29)
, (3.29)
pentru ca din (3.3) rezulta ca
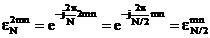 . (3.30)
. (3.30)
Raman de rezolvat cateva probleme legate
de organizarea datelor si calculelor. In (3.27) se observa
variabilele intermediare 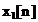 si
si  pot fi calculate
simultan din
pot fi calculate
simultan din  si
si 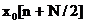 si ca
rezultatele raman "in situ".
si ca
rezultatele raman "in situ".
In (3.28) se observa ca variabilele
intermediare 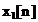 ,
,  care intra in formula
de calcul a esantioanelor pare de frecventa sunt ordonate in
sens crescator in prima jumatate a vectorului. Daca se face
substitutia
care intra in formula
de calcul a esantioanelor pare de frecventa sunt ordonate in
sens crescator in prima jumatate a vectorului. Daca se face
substitutia  in (3.29), tinand
cont de (3.23), se obtine formula de calcul a esantioanelor impare de
frecventa
in (3.29), tinand
cont de (3.23), se obtine formula de calcul a esantioanelor impare de
frecventa
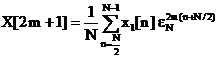 ,
,  , (3.31)
, (3.31)
unde variabilele intermediare 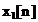 ,
,  sunt ordonate in sens
crescator in a doua jumatate a vectorului.
sunt ordonate in sens
crescator in a doua jumatate a vectorului.
Formulele (3.28), (3.30) si (3.31)
demonstreaza ca o iteratie a algoritmului dubleaza numarul
de transformate Fourier rapide si le injumatateste
dimensiunea si ca sunt necesare  iteratii pentru
aflarea valorii esantioanelor de frecventa.
iteratii pentru
aflarea valorii esantioanelor de frecventa.
Ordonarea esantioanelor de frecventa
Din (3.28) si (3.31) rezulta
dupa prima iteratie esantioanele de frecventa sunt amestecate.
Acest proces de amestecare continua si in iteratiile
urmatoare deci demonstratia din sectiunea anterioara trebuie
completata cu un algoritm de ordonare finala a esantioanelor
de frecventa.
In practica nu se memoreaza vectorul
esantioanelor de frecventa pentru ca, dupa ultima
iteratie se obtine 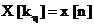 . Este suficient sa se gaseasca o functie
de forma:
. Este suficient sa se gaseasca o functie
de forma:
 ,
,  , (3.32)
, (3.32)
care sa indice pozitiile esantioanelor
de frecventa.
In sectiunea precedenta s‑a
aratat ca dupa fiecare iteratie a unei transformate Fourier
rapide esantioanele de frecventa sunt sortate: intai cele pare
in prima jumatate a vectorului, apoi cele impare sunt asezate in
ordine crescatoare in a doua jumatate a vectorului.
In tabelul figura 3.2 se da un exemplu
pentru  . In prima coloana se gaseste n indexul pentru
vectorul
. In prima coloana se gaseste n indexul pentru
vectorul  , in a doua coloana se gaseste
, in a doua coloana se gaseste  scris cu cifre binare
iar in a doua coloana se gaseste
scris cu cifre binare
iar in a doua coloana se gaseste 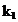 scris tot cu cifre
binare.
scris tot cu cifre
binare.

Figura
3.2. Metoda de calcul a indecsilor  ,
, 
Ordonarea descrisa anterior consta
in luarea primei cifre binare din fiecare numar 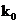 si asezarea
ei la sfarsitul numarului. In sectiunea 3.2.1 s‑a
aratat ca dupa prima iteratie se obtin doua
transformate Fourier rapide de dimensiune
si asezarea
ei la sfarsitul numarului. In sectiunea 3.2.1 s‑a
aratat ca dupa prima iteratie se obtin doua
transformate Fourier rapide de dimensiune 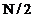 . Coloana a doua a tabelului contine numerele
. Coloana a doua a tabelului contine numerele 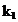 . Primele trei cifre binare din numerele
. Primele trei cifre binare din numerele 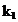 sunt indexul
variabilei intermediare care intra in transformata Fourier rapida
de dimensiune
sunt indexul
variabilei intermediare care intra in transformata Fourier rapida
de dimensiune 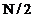 .
.
In coloana a treia a tabelului se gasesc
numerele  . Numerele
. Numerele  se obtin prin
luarea primei cifre binare din grupul de trei cifre binare si
asezarea ei in ultima pozitie a grupului. Dupa doua
iteratii se obtin patru transformate Fourier rapide de dimensiune
se obtin prin
luarea primei cifre binare din grupul de trei cifre binare si
asezarea ei in ultima pozitie a grupului. Dupa doua
iteratii se obtin patru transformate Fourier rapide de dimensiune  . Primele doua cifre binare din numerele
. Primele doua cifre binare din numerele  sunt indexul
variabilei intermediare care intra in transformata Fourier rapida
de dimensiune
sunt indexul
variabilei intermediare care intra in transformata Fourier rapida
de dimensiune  .
.
Dupa trei iteratii 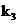 are cifrele binare ale
numarului
are cifrele binare ale
numarului  asezate in ordine
inversa. Daca numerele
asezate in ordine
inversa. Daca numerele  si
si 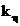 se scriu cu
se scriu cu  cifre binare atunci
pozitia finala a esantionului de frecventa se
afla inversand ordinea cifrelor binare si functia (3.32) devine:
cifre binare atunci
pozitia finala a esantionului de frecventa se
afla inversand ordinea cifrelor binare si functia (3.32) devine:
 ,
,  . (3.33)
. (3.33)
Programarea
algoritmului FFT
Pentru scrierea unui program care sa
implementeze algoritmul FFT, demonstratia prezentata anterior
trebuie completata prin precizarea urmatoarelor probleme:
care este memoria necesara pentru rularea
unui program de dimensiune 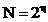 ;
;
cum se calculeaza simultan variabilele
intermediare cu formulele (3.27) astfel incat calculele sa se faca
"in situ";
cum se calculeaza indecsii necesari
pentru parcurgerea vectorului variabilelor intermediare si vectorul
exponentialelor in iteratiile 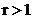 stiind ca la
fiecare iteratie dimensiunea transformatei se
injumatateste si se dubleaza numarul de transformate
Fourier rapide;
stiind ca la
fiecare iteratie dimensiunea transformatei se
injumatateste si se dubleaza numarul de transformate
Fourier rapide;
cum se face ordonarea finala a
esantioanelor de frecventa tinand seama de operatiile
de sortare a vectorului variabilelor intermediare (3.29) si (3.31).
Organizarea datelor
In memoria calculatorului se rezerva:
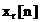 ,
,  , un vector de numere complexe folosit pentru memorarea
variabilelor intermediare;
, un vector de numere complexe folosit pentru memorarea
variabilelor intermediare;
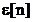 ,
,  , un vector pentru memorarea exponentialelor complexe;
, un vector pentru memorarea exponentialelor complexe;
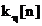 ,
,  , un vector de numere intregi fara semn in care se
memoreaza functia (3.33) tabelata. In sectiunea 3.3.4 se
prezinta algoritmul prin care se genereaza acest vector.
, un vector de numere intregi fara semn in care se
memoreaza functia (3.33) tabelata. In sectiunea 3.3.4 se
prezinta algoritmul prin care se genereaza acest vector.

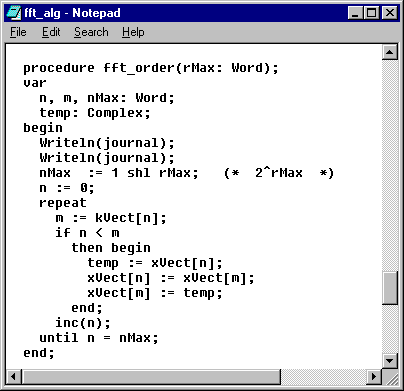
Figura
3.3. Alocarea memoriei
In figura 3.3 se prezinta
declaratiile prin care se aloca memoria necesara pentru vectorii
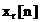 ,
, 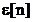 si
si 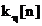 . Daca se face alocare statica a memoriei, de
regula se declara spatii mai mari decat cele necesare in rularea
respectiva. Daca se face alocare dinamica atunci, in timpul
rularii programului se pot aloca exact spatiile necesare.
. Daca se face alocare statica a memoriei, de
regula se declara spatii mai mari decat cele necesare in rularea
respectiva. Daca se face alocare dinamica atunci, in timpul
rularii programului se pot aloca exact spatiile necesare.
Vectorii 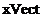 si
si  sunt formati din
obiecte din clasa
sunt formati din
obiecte din clasa  . Clasa are doua campuri
. Clasa are doua campuri  si
si 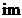 si metode care
implementeaza operatiile de adunare, scadere, inmultire,
calculul modulului si a fazei. In sectiunea 3.3.2 se va prezenta
modul in care se folosesc metodele clasei
si metode care
implementeaza operatiile de adunare, scadere, inmultire,
calculul modulului si a fazei. In sectiunea 3.3.2 se va prezenta
modul in care se folosesc metodele clasei  .
.
La pornirea algoritmului FFT,  , in partea reala a numerelor complexe din vectorul
variabilelor intermediare se incarca in ordine esantioanele
semnalului analizat (v. formula (3.1)) iar partea imaginara este
anulata
, in partea reala a numerelor complexe din vectorul
variabilelor intermediare se incarca in ordine esantioanele
semnalului analizat (v. formula (3.1)) iar partea imaginara este
anulata
 . (3.34)
. (3.34)
In iteratiile,  numerele din vectorul
numerele din vectorul  nu au
semnificatie fizica. La incheierea algoritmului,
nu au
semnificatie fizica. La incheierea algoritmului, 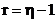 , vectorul
, vectorul 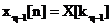 contine valorile
esantioanelor de frecventa care sunt amestecate
datorita ordonarilor care se fac in fiecare iteratie.
contine valorile
esantioanelor de frecventa care sunt amestecate
datorita ordonarilor care se fac in fiecare iteratie.
La pornirea algoritmului vectorul
exponentialelor complexe se initializeaza cu formula
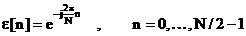 . (3.35)
. (3.35)
(v. notatia (3.3) din sectiunea
3.1.1). In figura 3.4 se prezinta procedura de initializare a
vectorului exponentialelor complexe.
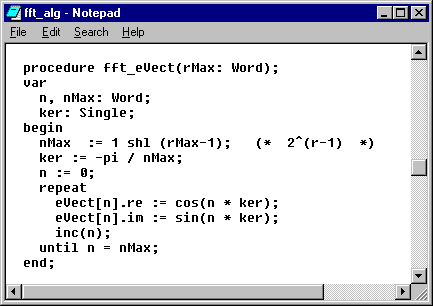
Figura
3.4. Initializarea vectorului exponentialelor complexe
Din formula (3.26) rezulta ca in
prima iteratie sunt necesare doar 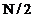 , iar in fiecare dintre iteratiile urmatoare
numarul exponentialelor complexe folosite in calcule se
injumatateste dar exponentialele se iau tot din
vectorul
, iar in fiecare dintre iteratiile urmatoare
numarul exponentialelor complexe folosite in calcule se
injumatateste dar exponentialele se iau tot din
vectorul 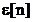 . In sectiunea 3.3.3 se va deduce o regula pentru
calculul indexului cu care se adreseaza vectorul exponentialelor
complexe.
. In sectiunea 3.3.3 se va deduce o regula pentru
calculul indexului cu care se adreseaza vectorul exponentialelor
complexe.
Organizarea calculelor
Un graf de fluenta se compune din
puncte si arce orientate. Un punct din care pornesc unul sau mai multe
arce este un operand initial. Un punct in care converge cel putin un
arc si din care porneste cel putin un arc este un operand
intermediar. Un punct din care nu porneste nici un arc este un rezultat.
Un nume scris langa un punct desemneaza o data
initiala, o variabila intermediara sau un rezultat.
Daca intr‑un punct converg mai
multe arce atunci in punctul respectiv se face o insumare. Daca intr‑un
punct converge un singur arc atunci se face doar operatia de atribuire.
Numarul scris in dreptul unui arc este ponderea cu care participa
operandul din punctul initial in operatia din punctul final.

Figura
3.5. Graful de fluenta al unui fluture
Graful de fluenta din figura 3.5
care implementeaza calculele din formulele (3.27) poarta numele
sugestiv de fluture. Un fluture calculeaza "in situ" variabilele
intermediare 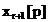 si
si  din variabilele
intermediare
din variabilele
intermediare  si
si 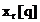 . In figura 3.6 se prezinta procedura care implementeaza
calculele dintr‑un fluture.
. In figura 3.6 se prezinta procedura care implementeaza
calculele dintr‑un fluture.
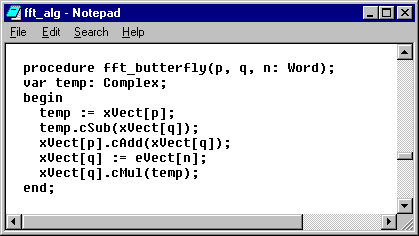
Figura
3.6. Implementarea unui fluture
Clasa  este organizata
ca o biblioteca aritmetica cu un singur operand. Campurile
este organizata
ca o biblioteca aritmetica cu un singur operand. Campurile  si
si 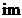 au rolul de
acumulator. Metodele
au rolul de
acumulator. Metodele  ,
, 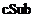 si
si 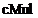 au ca parametru tot un
numar complex transmis prin valoare si implementeaza
operatiile aritmetice de adunare, scadere si respectiv
inmultire a numerelor complexe. Rezultatul operatiei ramane in
acumulator.
au ca parametru tot un
numar complex transmis prin valoare si implementeaza
operatiile aritmetice de adunare, scadere si respectiv
inmultire a numerelor complexe. Rezultatul operatiei ramane in
acumulator.
Indecsi
In figurile 3.5 si 3.6  este indexul pentru
prima linie a fluturelui,
este indexul pentru
prima linie a fluturelui,  indexul pentru a doua
linie a fluturelui iar
indexul pentru a doua
linie a fluturelui iar  este indexul pentru exponentiala
complexa. Calculul indecsilor
este indexul pentru exponentiala
complexa. Calculul indecsilor  ,
,  si
si  va fi detaliat in
sectiunea urmatoare.
va fi detaliat in
sectiunea urmatoare.
Pentru unificarea notatiilor, in afara
indexului pentru iteratii,  , se introduc doi indecsi noi ale caror limite
maxime de indexare se exprima in functie de
, se introduc doi indecsi noi ale caror limite
maxime de indexare se exprima in functie de  :
:
 pentru fluturii dintr‑o
transformata Fourier rapida;
pentru fluturii dintr‑o
transformata Fourier rapida;
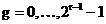 pentru grupurile de
fluturi. Un grup de fluturi corespunde cu o transformata Fourier rapida.
pentru grupurile de
fluturi. Un grup de fluturi corespunde cu o transformata Fourier rapida.
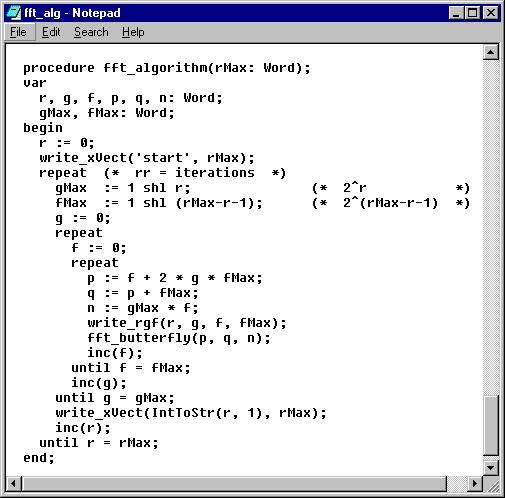
Figura
3.7. Generarea indecsilor in algoritmul FFT
In figura 3.7 se prezinta rutina care
genereaza indecsii  ,
,  si
si  , indexul folosit pentru adresarea vectorului
exponentialelor complexe. Se observa ca sunt trei bucle
controlate de indecsii
, indexul folosit pentru adresarea vectorului
exponentialelor complexe. Se observa ca sunt trei bucle
controlate de indecsii  , indexul pentru iteratii,
, indexul pentru iteratii,  , indexul pentru grupurile de fluturi si
, indexul pentru grupurile de fluturi si  , indexul pentru fluturi.
, indexul pentru fluturi.
In prima iteratie  exista un singur
grup de
exista un singur
grup de 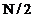 fluturi. Regula de
indexare rezulta din formulele (3.27)
fluturi. Regula de
indexare rezulta din formulele (3.27)  ,
, 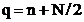 . In iteratia urmatoare
. In iteratia urmatoare  si lucrurile se
complica pentru ca sunt doua transformate Fourier Rapide de
dimensiune
si lucrurile se
complica pentru ca sunt doua transformate Fourier Rapide de
dimensiune 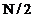 deci sunt doua
grupuri de cate
deci sunt doua
grupuri de cate  fluturi.
fluturi.
In cazul general, fiecare transformata
Fourier rapida de dimensiune  are cate un grup
are cate un grup 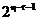 de fluturi, iar a
doua linie a unui fluture se afla la distanta de
de fluturi, iar a
doua linie a unui fluture se afla la distanta de 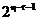 fata de
prima linie. Indecsii
fata de
prima linie. Indecsii  ,
,  si
si  se calculeaza
cu urmatoarele formule:
se calculeaza
cu urmatoarele formule:
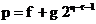 ,
,  ,
,  (3.36)
(3.36)
In prima iteratie vectorul 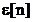 este parcurs in ordine
complet. La injumatatirea dimensiunii transformatei Fourier
rapide se injumatateste si dimensiunea vectorului
exponentialelor complexe, dar exponentialele divizeaza
uniform tot o jumatate de cerc. Din (3.30) rezulta ca
este parcurs in ordine
complet. La injumatatirea dimensiunii transformatei Fourier
rapide se injumatateste si dimensiunea vectorului
exponentialelor complexe, dar exponentialele divizeaza
uniform tot o jumatate de cerc. Din (3.30) rezulta ca  , deci vectorul
, deci vectorul 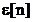 este parcurs din
doua in doua valori, ceea ce demonstreaza formula
este parcurs din
doua in doua valori, ceea ce demonstreaza formula  .
.
La scrierea unui program care
implementeaza algoritmul FFT cea mai complicata problema este
calculul corect al indecsilor  ,
,  si
si  . In aceasta fata de dezvoltare a programului
procedurile
. In aceasta fata de dezvoltare a programului
procedurile 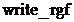 si
si  nu fac decat sa
scrie intr‑un fisier text indecsii
nu fac decat sa
scrie intr‑un fisier text indecsii  ,
,  ,
,  ,
,  ,
,  si
si  sub forma unui tabel.
Dupa verificarea corectitudinii indecsilor se inlatura
apelul procedurii
sub forma unui tabel.
Dupa verificarea corectitudinii indecsilor se inlatura
apelul procedurii 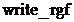 iar procedura
iar procedura  va avea continutul
din figura 3.6.
va avea continutul
din figura 3.6.
Algoritmul de ordonare
Fie un numar intreg fara semn
oarecare, cu  cifre binare
cifre binare 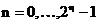 . Algoritmul care implementeaza functia (3.3.3)
este complicat pentru ca nu exista o succesiune simpla de instructiuni
scrise in limbaj de asamblare sau in limbaj de nivel inalt care sa inverseze
ordinea cifrelor binare.
. Algoritmul care implementeaza functia (3.3.3)
este complicat pentru ca nu exista o succesiune simpla de instructiuni
scrise in limbaj de asamblare sau in limbaj de nivel inalt care sa inverseze
ordinea cifrelor binare.
Din acest motiv in practica foloseste
un algoritm iterativ care genereaza direct numerele binare cu cifrele
asezate in ordine inversa. In memorie se declara vectorul  ,
, 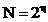 si se
initializeaza
si se
initializeaza  ,
, 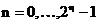 . Apoi, tabelul functiei (3.3.3) se genereaza cu
formulele iterative:
. Apoi, tabelul functiei (3.3.3) se genereaza cu
formulele iterative:
 ,
,  ,
, 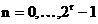 (3.37)
(3.37)
Se observa ca la fiecare
iteratie algoritmul dubleaza lungimea vectorului si ca
algoritmul poate continua pana la orice dimensiune. Prima dintre formulele
3.37 adauga o cifra binara 0 la sfarsitul numarului
iar a doua formula adauga o cifra binara 1 la
sfarsitul numarului.
In figura 3.5 se prezinta algoritmul de
generare a numerelor binare asezate in ordine inversa pentru 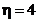 , deci sunt necesare patru iteratii indexate
, deci sunt necesare patru iteratii indexate 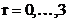 .
.

Figura
3.8. Algoritmul de generare a numerelor binare asezate in ordine
inversa
In prima coloana a tabelului se
gaseste indexul 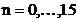 , in coloanele urmatoare se gasesc numerele
, in coloanele urmatoare se gasesc numerele  ,
, 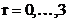 , obtinute dupa fiecare iteratie iar in ultima
coloana se gaseste
, obtinute dupa fiecare iteratie iar in ultima
coloana se gaseste  scris cu cifre
zecimale. Functia discreta (3.3.3) de forma
scris cu cifre
zecimale. Functia discreta (3.3.3) de forma 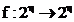 da pozitiile
adevarate a esantioanelor de frecventa. Prima si
ultima coloana din tabel sunt functia (3.3.3) tabelata.
da pozitiile
adevarate a esantioanelor de frecventa. Prima si
ultima coloana din tabel sunt functia (3.3.3) tabelata.

Figura
3.9. Procedura care genereaza vectorul 
Figura
3.10. Procedura de ordonare a esantioanelor de frecventa
In figura 3.2 se prezinta procedura care
ordoneaza esantioanele de frecventa dupa incheierea
rularii algoritmului FFT. Din tabelele din figurile 3.2 si 3.8
rezulta ca sunt cateva esantioane de frecventa care
iti pastreaza pozitia. In celelalte cazuri
esantioanele de frecventa cu pozitiile  si
si  trebuie schimbate
intre ele.
trebuie schimbate
intre ele.
La parcurgerea completa a vectorului  perechea de
indecsi
perechea de
indecsi  si
si 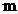 este intalnita de
doua ori. Esantioanele de frecventa
este intalnita de
doua ori. Esantioanele de frecventa 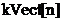 si
si 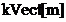 se sunt schimbate
intre ele daca
se sunt schimbate
intre ele daca  . In acest fel se evita schimbarea esantioanelor de
frecventa care isi pastreaza pozitia si se
evita ca esantioanele de frecventa
. In acest fel se evita schimbarea esantioanelor de
frecventa care isi pastreaza pozitia si se
evita ca esantioanele de frecventa 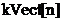 si
si 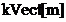 sa fie schimbate
intre ele de doua ori.
sa fie schimbate
intre ele de doua ori.
Concluzii
Din acest capitol se desprind doar doua
concluzii in comparatie cu transformata Fourier discreta algoritmul
FFT este eficient dar este complicat.
Eficienta calculelor
Daca calculele se fac cu transformata
Fourier discreta pusa sub forma matriceala (v. (3.5),
sectiunea 3.1.1) atunci pentru calculul unui esantion de
frecventa sunt necesare 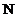 inmultiri si
inmultiri si
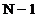 adunari. In
consecinta, pentru calculul celor
adunari. In
consecinta, pentru calculul celor 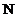 esantioane de
frecventa sunt necesare
esantioane de
frecventa sunt necesare  inmultiri si
inmultiri si
 adunari.
adunari.
Fiecare transformata Fourier rapida
de dimensiune  are cate un grup
are cate un grup 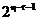 de fluturi. In
iteratia respectiva sunt
de fluturi. In
iteratia respectiva sunt 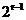 transformate Fourier rapide, deci in fiecare iteratie se
calculeaza
transformate Fourier rapide, deci in fiecare iteratie se
calculeaza  fluturi.
fluturi.
Pentru calculul unui fluture sunt necesare
doua adunari si o inmultire, deci intr‑o
iteratie sunt necesare 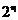 adunari si
adunari si  inmultiri.
Algoritmul are
inmultiri.
Algoritmul are  iteratii deci in
total sunt necesare
iteratii deci in
total sunt necesare  adunari si
adunari si 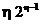 inmultiri.
inmultiri.
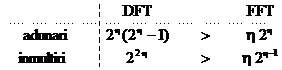
Figura
3.11. Eficienta algoritmului FFT
In tabelul din figura 3.11 sunt comparate
numarul de operatii aritmetice necesare pentru transformata Fourier
discreta de dimensiune 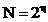 si pentru
algoritmul FFT. Se observa ca algoritmul reduce mult numarul
operatiilor aritmetice necesare pentru calculul spectrului discret.
si pentru
algoritmul FFT. Se observa ca algoritmul reduce mult numarul
operatiilor aritmetice necesare pentru calculul spectrului discret.
De ce FFT este un algoritm complicat?
Argumentatie:
in subcapitolul 3.4.1 se precizeaza
notiunile si notatiile cu care opereaza transformata Fourier
Discreta. Subcapitolul Sectiunea 3.4.1 este simpla in comparatie
cu cele urmatoare;
in subcapitolul 3.4.2 se prezinta
demonstratia unei variante a algoritmului FFT cunoscuta sub numele
decimation‑in‑frequency FFT Algorithm. In demonstratie intervin multe schimbari de
variabila si multe notatii;
in subcapitolul 3.4.3 se definesc structurile
de date ale programului care implementeaza algoritmul FFT si modul
de organizare a calculelor (v. sectiunea 3.3.2). Se folosesc trei
indecsi independenti  ,
,  si
si  si inca trei
indecsi
si inca trei
indecsi  ,
,  si
si  calculati din primii trei cu formulele (3.37).
calculati din primii trei cu formulele (3.37).
Din aceste motive, in timp, s‑au
incercat mai multe variante de demonstrare si de implementare ale
algoritmului FFT. Toate eforturile s‑au soldat cu acelasi rezultat:
complexitatea algoritmului se pastreaza in oricare dintre
variantele lui.
De exemplu, in algoritmul cunoscut sub numele
decimation‑in‑time FFT Algorithm, se demonstreaza
ca prin agregarea a doua transformate Fourier rapide de dimensiune
N, se obtine o transformata Fourier rapida de dimensiune 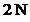 . Demonstratia
decurge in sens invers fata de ceea prezentata in subcapitolul
3.4.2. Pentru ca toate functiile care apar in implementarea unei
transformate DFT discrete sunt liniare, atunci este evident ca aceste
functii sunt inversabile si ca algoritmul poate redactat in
ordine inversa. Deci rezultatele sunt reversibile.
. Demonstratia
decurge in sens invers fata de ceea prezentata in subcapitolul
3.4.2. Pentru ca toate functiile care apar in implementarea unei
transformate DFT discrete sunt liniare, atunci este evident ca aceste
functii sunt inversabile si ca algoritmul poate redactat in
ordine inversa. Deci rezultatele sunt reversibile.
Bibliografie
Popescu D. Prelucrarea digitala a
semnalelor. Editura ICPE Bucuresti 2000.
Pop E., I. Nafornita, V.
Tiponut, A. Mihaescu, L. Toma. Metode in prelucrarea semnalelor.
Editura Facla, Timisoara, 1986.
Proakis J.G., D. G. Manolakis. Digiral Signal
Processing, Principles, Aghorithms and Applications. Thire Edittion. Prince /
Hall International, Inc., 1996.
Oppenhiem A.V., Schaffer R. V. Digiral Signal Processing. Prince / Hall
International, Inc.
Gade S., H. Herlufsen: Use of Weighting
Functions in DFT / FFT Analysis (Part I).
Brüel & Kjær Teckhnical Rewiew, No. 3
1997;





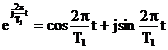







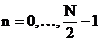 . (3.27)
. (3.27)