Analiza matematica - Definitii si teoreme ptr examen
Definitii
1.Fie f: D  , D
, D 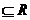
 ,c punct de acumulare ce apartine lui D. Daca exista ,
,c punct de acumulare ce apartine lui D. Daca exista , 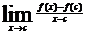
 se numeste derivata lui f in c si se noteaza f '(c).
Spunem in acest caz ca f este derivabila in c.
se numeste derivata lui f in c si se noteaza f '(c).
Spunem in acest caz ca f este derivabila in c.
Legatura dintre derivabilitate si continuitate : Fie f:D , D
, D 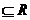
 ,c punct de acumulare al lui D ce apartine lui D. Daca f este
derivabila in c rezulta f continua in c. (Continuitatea este o conditie
necesara pentru derivabilitate dar nu si suficienta. Exemplu: f:R
,c punct de acumulare al lui D ce apartine lui D. Daca f este
derivabila in c rezulta f continua in c. (Continuitatea este o conditie
necesara pentru derivabilitate dar nu si suficienta. Exemplu: f:R  ,f(x)=|x|, pentru orice x din R)
,f(x)=|x|, pentru orice x din R)
2. Fie f:D ,D
,D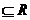 si c un punct din D.
si c un punct din D.
c se numeste punct de maxim local(relativ) al
functiei f daca exista 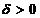 astfel incat pentru orice
astfel incat pentru orice  avem
avem 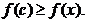
c se numeste punct de minim local(relativ) al
functiei f daca exista 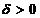 astfel pentru orice
astfel pentru orice  avem
avem 
3.a)Fie f:D unde
unde 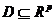 si c punct interior al
lui D si fie
si c punct interior al
lui D si fie 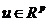 .Un vector
.Un vector  se numeste derivata lui f in c dupa vectorul u (sau dupa
directia u daca ||u||=1), daca exista limita
se numeste derivata lui f in c dupa vectorul u (sau dupa
directia u daca ||u||=1), daca exista limita 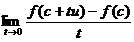 si
si  .
.
b)Fie f:D unde
unde 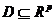 si c punct interior al
lui D. Fie pentru orice
si c punct interior al
lui D. Fie pentru orice  ,
,  unde 1 este pe pozitia i. Atunci daca exista
unde 1 este pe pozitia i. Atunci daca exista  ,respectiv
,respectiv  ele se numesc derivata
partiala a lui f in c in raport cu variabilele
ele se numesc derivata
partiala a lui f in c in raport cu variabilele respectiv derivata partiala a lui f in raport cu
variabilele
respectiv derivata partiala a lui f in raport cu
variabilele .
.
4. Fie  . f este diferentiabila (derivabila) in c daca exista
o aplicatie liniara
. f este diferentiabila (derivabila) in c daca exista
o aplicatie liniara  ( ie
( ie  ) astfel incat
) astfel incat 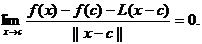
5. Pentru o functie 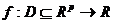 si
si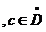 astfel incat exista si sunt continue derivatele partiale de
ordinul al II-lea ale lui f pe o vecinatate a lui c, definim diferentiala de
ordin 2 a lui f in c ca fiind aplicatia :
astfel incat exista si sunt continue derivatele partiale de
ordinul al II-lea ale lui f pe o vecinatate a lui c, definim diferentiala de
ordin 2 a lui f in c ca fiind aplicatia : 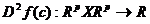 ,data de
,data de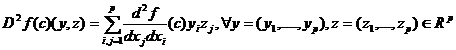 .
.
Analog pentru o functie 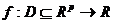 si
si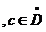 astfel incat exista si sunt continue derivatele partiale de
ordin 3ale lui f in c, definim diferentiala de ordin 3 ca fiind
aplicatia
astfel incat exista si sunt continue derivatele partiale de
ordin 3ale lui f in c, definim diferentiala de ordin 3 ca fiind
aplicatia 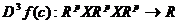 data de
data de
 Analog se defineste diferentiala de orice ordin intr-un
punct.
Analog se defineste diferentiala de orice ordin intr-un
punct.
6.Fie functia 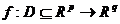 si
si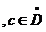 .Daca derivatele partiale de ordin 1 exista si sunt continue
in c spunem ca f este de clasa C1 in c. Daca
.Daca derivatele partiale de ordin 1 exista si sunt continue
in c spunem ca f este de clasa C1 in c. Daca  si f este de clasa C1 in orice punct din D0
spunem ca f este de clasa C1 pe D0.
si f este de clasa C1 in orice punct din D0
spunem ca f este de clasa C1 pe D0.
7. Fie  marginite. O suma Riemann-Stieltjes a lui f in raport
cu g corespunzatoare partitiei
marginite. O suma Riemann-Stieltjes a lui f in raport
cu g corespunzatoare partitiei 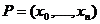 a lui [a,b] are forma
a lui [a,b] are forma 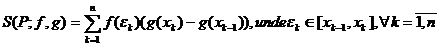 .( O partitie (sau diviziune) a lui [a,b]este o familie
finita de intervale inchise care au in comun cel mult un punct si a caror
reuniune este [a,b]).
.( O partitie (sau diviziune) a lui [a,b]este o familie
finita de intervale inchise care au in comun cel mult un punct si a caror
reuniune este [a,b]).
(*)Fie  marginite. Spunem ca f este integrabila Riemann-Stieltjes in raport cu g daca exista un numar real I cu
proprietatea ca pentru
marginite. Spunem ca f este integrabila Riemann-Stieltjes in raport cu g daca exista un numar real I cu
proprietatea ca pentru  partitie a lui [a,b] astfel incat pentru orice partitie P
care este rafinare a lui
partitie a lui [a,b] astfel incat pentru orice partitie P
care este rafinare a lui  si orice suma Riemann-Stieltjes S(P;f,g) corespunzatoare lui
P avem
si orice suma Riemann-Stieltjes S(P;f,g) corespunzatoare lui
P avem 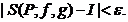 In acest caz I este unic determinat si se numeste integrala
Riemann-Stieltjes a lui f in raport cu g si notam
In acest caz I este unic determinat si se numeste integrala
Riemann-Stieltjes a lui f in raport cu g si notam 
Cand g(x)=0, pentru orice x din [a,b] spunem ca f
este integrabila Riemann.
8. Un interval inchis din 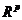 este o submultime J a
lui
este o submultime J a
lui 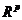 de forma
de forma 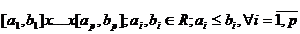 . Masura lui J este numarul
. Masura lui J este numarul 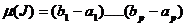 .
.
O
submultime Z a lui 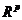 se numeste de masura nula daca pentru orice
se numeste de masura nula daca pentru orice 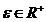 exista o familie finita
exista o familie finita  de intervale inchise astfel incat Z este continuta in reuniunea
elementelor acestei familii si
de intervale inchise astfel incat Z este continuta in reuniunea
elementelor acestei familii si 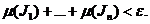
(Pentru
D o submultime marginita a lui 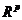 care are frontiera de
masura nula , spunem ca D este masurabila si definim masura lui D notata cu
A(D) ca fiind
care are frontiera de
masura nula , spunem ca D este masurabila si definim masura lui D notata cu
A(D) ca fiind  )
)
9.Fie 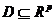 o multime compacta iar
o multime compacta iar
 o functie marginita. O suma Riemann a lui f corespunzatoare
partitiei
o functie marginita. O suma Riemann a lui f corespunzatoare
partitiei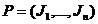 a lui
a lui 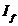 are forma
are forma  Un element
Un element  se numeste integrala Riemann a lui f daca pentru orice
se numeste integrala Riemann a lui f daca pentru orice
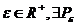 partitie a lui
partitie a lui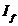 astfel incat pentru orice partitie P care este rafinare a lui
astfel incat pentru orice partitie P care este rafinare a lui
 si orice suma Riemann
S(P;f) corespunzatoare lui P avem
si orice suma Riemann
S(P;f) corespunzatoare lui P avem 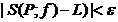 . In acest caz L este unic determinat nu depinde de
. In acest caz L este unic determinat nu depinde de 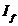 si se numeste
integrala Riemann a lui f pe D si se noteaza
si se numeste
integrala Riemann a lui f pe D si se noteaza 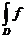 sau,pentru p=2
sau,pentru p=2 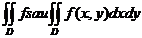 sau pentru p=3
sau pentru p=3 
10. Fie  ,f o functie cu valori reale al carei domeniu de definitie
contine pe (a,b]. Presupunem f este integrabila Riemann pe orice interval [c,b]
unde
,f o functie cu valori reale al carei domeniu de definitie
contine pe (a,b]. Presupunem f este integrabila Riemann pe orice interval [c,b]
unde 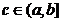 si notam
si notam 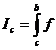 .Definim integrala improprie a lui f pe J=[a,b] ca
fiind
.Definim integrala improprie a lui f pe J=[a,b] ca
fiind 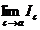 .
.
In cadrul de mai sus daca exista I numar real astfel
incat pentru  astfel incat pentru
astfel incat pentru  spunem ca I este integrala improprie a lui f pe
J=[a,b] si vom nota aceasta valoare prin
spunem ca I este integrala improprie a lui f pe
J=[a,b] si vom nota aceasta valoare prin 
11.In cadrul definitiei 10 ,in cazul in care exista
, 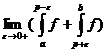 se noteaza cu (CPN)
se noteaza cu (CPN)  si se va numi valoarea
principala Cauchy a integralei.
si se va numi valoarea
principala Cauchy a integralei.
12. a)Fie  .Daca exista
.Daca exista 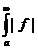 atunci spunem ca f este absolut integrabila pe
atunci spunem ca f este absolut integrabila pe 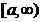 sau ca
sau ca 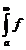 converge absolut.
converge absolut.
b)Fie 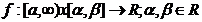 . Presupunem ca pentru
. Presupunem ca pentru  Vom spune ca aceasta convergenta este uniforma (in
raport cu
Vom spune ca aceasta convergenta este uniforma (in
raport cu  ) daca pentru
) daca pentru 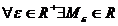 astfel incat pentru orice
astfel incat pentru orice 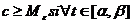 avem
avem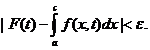 .Definitii similare exista si pentru
.Definitii similare exista si pentru 
13.Daca 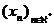 sir de elemente din
sir de elemente din 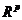 definim seria generata de
definim seria generata de 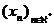 ca fiind sirul
ca fiind sirul  .Daca S este convergent limita lui S se numeste suma
seriei.
.Daca S este convergent limita lui S se numeste suma
seriei.
14.Daca 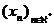 este un sir de elemente din
este un sir de elemente din 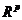 spunem ca seria
spunem ca seria 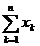 este absolut convergenta daca seria
este absolut convergenta daca seria 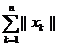 este convergenta. O serie se numeste semiconvergenta daca
este convertgenta dar nu este absolut convergenta.
este convergenta. O serie se numeste semiconvergenta daca
este convertgenta dar nu este absolut convergenta.
15. Pentru seriile  cu termeni din
cu termeni din 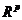 se defineste produsul Cauchy al lor ca fiind seria
se defineste produsul Cauchy al lor ca fiind seria  .
.
16.a)Daca  sir de functii cu
sir de functii cu 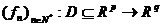 ,iar sirul sumelor sale partiale
,iar sirul sumelor sale partiale  unde
unde  converge pe D catre
converge pe D catre 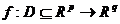 spunem ca seria
spunem ca seria  converge pe D
catre f.
converge pe D
catre f.
b)Daca
pentru 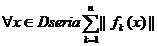 converge spunem ca seria
converge spunem ca seria  converge absolut pe D.
converge absolut pe D.
c)Daca  converge uniform catre
converge uniform catre 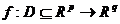 spunem ca seria
spunem ca seria  converge uniform
pe D catre f.
converge uniform
pe D catre f.
17.O serie de functii  se numeste serie de puteri in jurul lui c daca pentru
se numeste serie de puteri in jurul lui c daca pentru  astfel incat
astfel incat 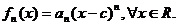
18.Fie 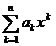 o serie de puteri.Daca sirul
o serie de puteri.Daca sirul  este marginit fie
este marginit fie  .Daca sirul
.Daca sirul  este nemarginit fie
este nemarginit fie 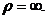 Definim raza de convergenta a serie de puteri
Definim raza de convergenta a serie de puteri 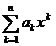 ca fiind
ca fiind 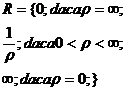 .
.
TEOREME
Teorema lui Fermat: Fie 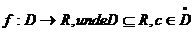 punct de maxim(sau minim)local al functiei f. Daca f este
derivabila in c atunci f '(c)=0.
punct de maxim(sau minim)local al functiei f. Daca f este
derivabila in c atunci f '(c)=0.
2.Teorema lui Rolle: Fie  ,f continua pe [a,b] si derivabila pe (a,b)astfel incat
f(a)=f(b).Atunci exista un punct
,f continua pe [a,b] si derivabila pe (a,b)astfel incat
f(a)=f(b).Atunci exista un punct  astfel incat f '(c)=0.
astfel incat f '(c)=0.
3.Teorema Lagrange : Fie  ,f continua pe [a,b] si derivabila pe (a,b). Atunci exista un
punct
,f continua pe [a,b] si derivabila pe (a,b). Atunci exista un
punct  astfel incat
astfel incat 
4.Teorema lui Cauchy: Fie 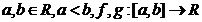 ,continue pe [a,b] si derivabile pe (a,b). Atunci exista un
punct
,continue pe [a,b] si derivabile pe (a,b). Atunci exista un
punct  astfel incat
astfel incat 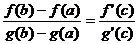 .
.
5.Teorema lui Darboux : Fie  ,unde I este un interval din R, o functie derivabila. Atunci
pentru orice J, interval inclus in I, f '(J)este interval.
,unde I este un interval din R, o functie derivabila. Atunci
pentru orice J, interval inclus in I, f '(J)este interval.
6.Teorema lui Taylor : Fie 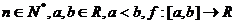 o functie cu urmatoarele proprietati: exista
o functie cu urmatoarele proprietati: exista  si sunt continue si exista
si sunt continue si exista  .Atunci pentru orice
.Atunci pentru orice 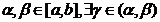 astfel incat
astfel incat  .
.
7.Regula lui L'Hopital Fie 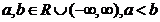 si I un interval din R astfel incat
si I un interval din R astfel incat 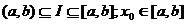 .Se considera doua functii
.Se considera doua functii  cu urmatoarele proprietati:
cu urmatoarele proprietati:
a) 
b) f si g sunt derivabile si
g'(x)  0 pentru orice
0 pentru orice 
c) exista 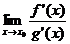
Atunci:
i)g(x)  0 pentru orice
0 pentru orice  (respectiv exista o vecinatate V a lui
(respectiv exista o vecinatate V a lui 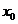 astfel incat g(x)
astfel incat g(x) 
ii)exista 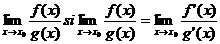
8.Teorema de pemutare a limitei cu derivata Fie  un sir de functii unde pentru
un sir de functii unde pentru 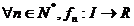 unde I interval marginit din R. Sa presupunem ca exista
unde I interval marginit din R. Sa presupunem ca exista 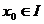 astfel incat sirul
astfel incat sirul  converge,ca,pentru
converge,ca,pentru 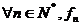 este derivabila si ca sirul
este derivabila si ca sirul  converge uniform pe I catre o functie derivabila
converge uniform pe I catre o functie derivabila  si mai mult f '=g.
si mai mult f '=g.
9.Caracterizarea derivabilitatii pentru functii
de o variabila reala
Fie  .Atunci urmatoarele afirmatii sunt echivalente:
.Atunci urmatoarele afirmatii sunt echivalente:
a) f este derivabila in c
b) exista o aplicatie liniara 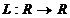 ( ie
( ie 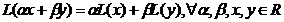 )
)
astfel incat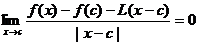 .
.
10.Legatura dintre diferentiabilitate si
continuitate
Fie  . Daca f este diferentiabila in c atunci exista
. Daca f este diferentiabila in c atunci exista  astfel incat pentru orice x din D cu proprietatea ca
astfel incat pentru orice x din D cu proprietatea ca 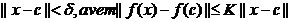 .In particular f este continua in c.
.In particular f este continua in c.
11.a)Legatura dintre diferentiabilitate si
existenta derivatelor partiale
Fie  .Daca f este diferentiabila in c atunci exista
.Daca f este diferentiabila in c atunci exista 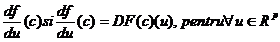 .
.
b)Criteriu
de diferentiabilitate
Fie  .Daca exista V o vecinatate a lui c pe care exista toate
derivatele partiale si sunt continue in c,atunci f este diferentiabila in c.
.Daca exista V o vecinatate a lui c pe care exista toate
derivatele partiale si sunt continue in c,atunci f este diferentiabila in c.
12.Operatii algebrice cu functii diferentiabile
Fie  .
.
a)Daca f si g sunt diferentiabile in c atunci  este diferentiabila in c si
este diferentiabila in c si  .
.
b)Daca f si g sunt diferentiabile in c atunci k=f*g
este diferentiabila si Dk(c)(u)=Df(c)(u)g(c)+f(c)Dg(c)(u) pentru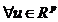
c)Daca  este diferentiabila in c atunci
este diferentiabila in c atunci  este diferentiabila in c si
este diferentiabila in c si 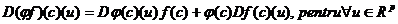 .
.
13.Teorema de diferentiabilitate a functiilor
compuse
Fie  astfel incat
astfel incat 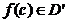 . Daca f este diferentiabila in c iar g diferentiabila in
. Daca f este diferentiabila in c iar g diferentiabila in 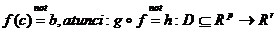 este diferentiabila in
c si
este diferentiabila in
c si 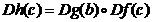
14.Teorema Lagrange-cazul multidimensional
Fie 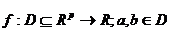 astfel incat
astfel incat  iar f este diferentiabila in orice punct din (a,b). Atunci
exista un punct
iar f este diferentiabila in orice punct din (a,b). Atunci
exista un punct  astfel incat
f(b)-f(a)=Df(c)(b-a)
astfel incat
f(b)-f(a)=Df(c)(b-a)
15.Teorema lui Schwarz
Fie 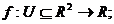 unde U este o vecinatate a lui (x,y) pentru care exista
unde U este o vecinatate a lui (x,y) pentru care exista  in orice punct din U
si astfel ca
in orice punct din U
si astfel ca  sa fie continua in (x,y).Atunci exista
sa fie continua in (x,y).Atunci exista 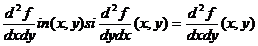 .
.
16.Teorema lui Taylor -cazul multidimensional Fie o
functie 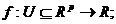 astfel incat pentru orice punct din (u,v) exista o vecinatate
a sa pe care exista si sunt continue derivatele partiale de ordin n ale lui f.
Atunci exista
astfel incat pentru orice punct din (u,v) exista o vecinatate
a sa pe care exista si sunt continue derivatele partiale de ordin n ale lui f.
Atunci exista 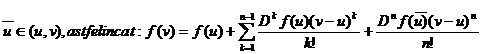 .
.
17. Teorema de injectivitate locala
Fie  .Daca f este de clasa C1
pe D si Df(c)este injectiva atunci exista
.Daca f este de clasa C1
pe D si Df(c)este injectiva atunci exista 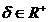 astfel incat
astfel incat 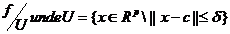 este injectiva.
este injectiva.
18.Teoreme de surjectivitate locala
Fie  . Daca f este de clasa C1 pe D si Df(c) este surjectiva atunci
exista
. Daca f este de clasa C1 pe D si Df(c) este surjectiva atunci
exista  astfel incat pentru
astfel incat pentru  si f(x)=y.
si f(x)=y.
19.Teorema aplicatiei deschise
Fie  de clasa C1pe D astfel ca Df(x)este surjectiva
pentru orice x din D.Atunci f(D) este deschisa. Mai mult pentru orice
de clasa C1pe D astfel ca Df(x)este surjectiva
pentru orice x din D.Atunci f(D) este deschisa. Mai mult pentru orice  , f(G) este deschisa.
, f(G) este deschisa.
20.Teorema de inversiune locala
Fie  de clasa C1pe
D si
de clasa C1pe
D si  astfel incat Df(c)este
injectiva. Atunci exista U o vecinatate a lui c cu proprietatea V=f(U) este o
vecinatate a lui f(c),f:U->V este bijectiva iar g=f-1:V->U
este continua . Mai mult g este de clasa C1 pe D si daca
astfel incat Df(c)este
injectiva. Atunci exista U o vecinatate a lui c cu proprietatea V=f(U) este o
vecinatate a lui f(c),f:U->V este bijectiva iar g=f-1:V->U
este continua . Mai mult g este de clasa C1 pe D si daca  iar x=g(y)
iar x=g(y)  U atunci Dg(y) = D(f-1) (f(x))=(Df(x))-1.
U atunci Dg(y) = D(f-1) (f(x))=(Df(x))-1.
21.Teorema functiilor implicite
Fie F o functie , 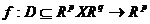 de clasa C1pe
o vecinatate a lui
de clasa C1pe
o vecinatate a lui 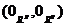 .
.
Presupunem ca F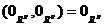 si ca aplicatia
si ca aplicatia  data de L(u)=DF
data de L(u)=DF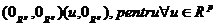 este bijectiva. Atunci exista o functie
este bijectiva. Atunci exista o functie  de clasa C1 pe
o vecinatate W a lui
de clasa C1 pe
o vecinatate W a lui 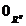 astfel incat
astfel incat  .
.
22.Teorema lui Ferma-cazul multidimensional
Fie  .Daca c este un punct de extrem local al lui f iar f este
diferentiabila in c atunci Df(c)=0.
.Daca c este un punct de extrem local al lui f iar f este
diferentiabila in c atunci Df(c)=0.
23.Criteriu de stabilire a punctelor de extrem
pentru functii de mai multe variabile
Fie  care are derivate partiale de ordin 2 continue si
care are derivate partiale de ordin 2 continue si  un punct critic al sau. Atunci:
un punct critic al sau. Atunci:
a) daca D2f(c)(w)2>0
 , atunci c este un punct de minim relativ al lui f.
, atunci c este un punct de minim relativ al lui f.
b) daca D2f(c)(w)2>0
 , atunci c este un punct de maxim relativ al lui f.
, atunci c este un punct de maxim relativ al lui f.
c) daca exista  astfel incat D2f(c)(w1)2>0
si D2f(c)(w2)2<0 atunci c este un punct sa
pentru f.
astfel incat D2f(c)(w1)2>0
si D2f(c)(w2)2<0 atunci c este un punct sa
pentru f.
24.Teorema multiplicatorilor lui Lagrange
Fie f si g clasa C1pe 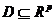 cu valori in R si
cu valori in R si 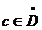 astfel incat g(c)=0. Presupunem ca exista V0
vecinatate a lui c astfel ca
astfel incat g(c)=0. Presupunem ca exista V0
vecinatate a lui c astfel ca 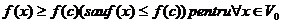 cu proprietatea suplimentara g(x)=0.
cu proprietatea suplimentara g(x)=0.
25.Criteriul Cauchy pentru integrala
Riemann-Stieltjes
Fie f,g:[a,b]->R,functii marginite,f este
integrabila Riemann-Stieltjes in raportcu g daca si numai daca pentru  partitie a lui [a,b] astfel ca pentru orice partitii P si Q
care sunt rafinari ale lui
partitie a lui [a,b] astfel ca pentru orice partitii P si Q
care sunt rafinari ale lui 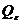 si orice sume Riemann-Stieltjes S(P;f,g) si S(Q;f,g)
corespunzatoare lui P, respectiv Q avem:|S(P;f,g)-S(Q;f.g)|<
si orice sume Riemann-Stieltjes S(P;f,g) si S(Q;f,g)
corespunzatoare lui P, respectiv Q avem:|S(P;f,g)-S(Q;f.g)|<  .
.
26.Teorema de integrare prin parti
Fie f,g:[a,b]->R, functii marginite. Atunci f
este integrabila Riemann-Stieltjes in raport cu g daca si numai daca g este
integrabila Riemann-Stieltjes in raport cu f caz in care avem:  .
.
27.Teorema de integrabilitate a functiilor continue
Fie f,g:[a,b]->R.Daca f este continua iar g este
monotona atunci f este integrabila Riemann-Stieltjes in raport cu g.
28.Teorema de permutare a limitei cu integrala
Fie g:[a,b]->R crescatoare iar  este un sir de functii integrabile Riemann-Stieltjes in
raport cu g care converge uniform catre f:[a,b]->R. Atunci f este
integrabila Riemann-Stieltjes in raport cu g si
este un sir de functii integrabile Riemann-Stieltjes in
raport cu g care converge uniform catre f:[a,b]->R. Atunci f este
integrabila Riemann-Stieltjes in raport cu g si 
29.Teorema convergentei marginite
Fie  un sir de functii
integrabile Riemann cu proprietatea ca exista M numar real astfel incat pentru
un sir de functii
integrabile Riemann cu proprietatea ca exista M numar real astfel incat pentru 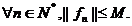 Daca
Daca  converge simplu catre
functia integrabila Riemann f:[a,b]->R atunci:
converge simplu catre
functia integrabila Riemann f:[a,b]->R atunci:  .
.
30.Teorema convergentei monotone
Fie  un sir monoton de
functii integrabile Riemann care converg simplu catre functia integrabila
Riemann f:[a,b]->R atunci:
un sir monoton de
functii integrabile Riemann care converg simplu catre functia integrabila
Riemann f:[a,b]->R atunci: 
31.Teorema de reprezentare a lui Riesz
Fie G:C([a,b])->R o functionala liniara pozitiva
si marginita. Atunci exista o functie crescatoare g:[a,b]->R astfel incat 
32.Prima teorema de medie
Fie f,g:[a,b]->R, g crescatoare iar f continua .
Atunci exista c din [a,b] astfel incat: 
33.a)Teorema de derivare:
Fie f,g :[a,b]->R, g crescatoare iar f continua.
Atunci ,daca g este derivabila in  , functia F:[a,b]->R data de F(x)=
, functia F:[a,b]->R data de F(x)= 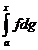 este derivabila in c si
este derivabila in c si  F'(c)=f(c)g'(c).
F'(c)=f(c)g'(c).
b)Teorema fundamentala a calculului integral.:
Fie f:[a,b]->R continua. Atunci o functie
F:[a,b]->R satisface relatia F(x)-F(a)=  daca si numai daca F'=f.
daca si numai daca F'=f.
34.Teorema de reducere a integralei
Riemann-Stieltjes la integrala Riemann
Fie f,g:[a,b]->R. Daca g este derivabila cu
derivata continua iar f este integrabila Riemann-Stieltjes in raport cu g ,
atunci fg' este integrabila Riemann si 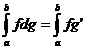 .
.
35.Prima teorema de medie pentru integrala Riemann
Fie f,g:[a,b]->R doua functii continue iar  .Atunci exista
.Atunci exista  astfel ca
astfel ca 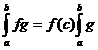 .
.
36.Teorema de integrare prin parti
Fie f,g:[a,b]->R doua functii derivabile cu
derivata continua .Atunci 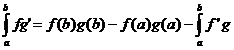 .
.
37.A doua teorema de medie
a)Fie f,g:[a,b]->R, f crescatoare iar g continua.
Atunci exista  astfel ca
astfel ca  .
.
c) Fie f,g:[a,b]->R, f
crescatoare iar g continua. Atunci exista  astfel ca
astfel ca 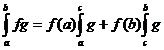 .
.
38.Teorema de schimbare de variabila
Fie 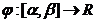 derivabila cu derivata continua atfel incat
derivabila cu derivata continua atfel incat  . Fie f o functie al carei domeniu de definitie include
imaginea functiei
. Fie f o functie al carei domeniu de definitie include
imaginea functiei  si care este continua pe imaginea lui
si care este continua pe imaginea lui  . Atunci :
. Atunci : 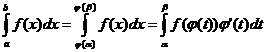 .
.
39.Formula lui Leibniz
Fie a,b,c,d  o functie continua
pentru care exista
o functie continua
pentru care exista 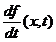 si este continua pe D.Fie
si este continua pe D.Fie  doua functii derivabile. Atunci functia data de
doua functii derivabile. Atunci functia data de  este derivabila si
este derivabila si  .
.
40.Teorema de inversare a ordinii de integrare
Fie a,b,c,d  o functie
continua.Atunci:
o functie
continua.Atunci:
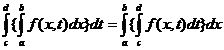 .
.
41.Formula lui Taylor
cu restul integral
Fie a,b 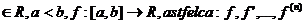 sa fie continue. Atunci :
sa fie continue. Atunci :  .
.
42.Criteriul lui Cauchy pentru integrala multipla
Fie 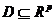 o multime compacta iar f:D->R o functie marginita. f este
integrabila Riemann pe D daca si numai daca pentru
o multime compacta iar f:D->R o functie marginita. f este
integrabila Riemann pe D daca si numai daca pentru 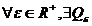 partitie a lui If, astfel ca pentru orice partitii
P si Q care sunt rafinari ale lui
partitie a lui If, astfel ca pentru orice partitii
P si Q care sunt rafinari ale lui 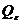 si orice sume Riemann
S(P;f)si S(Q;f) corespunzatoare lui P respectiv Q avem |S(P;f)-S(Q;f)|<
si orice sume Riemann
S(P;f)si S(Q;f) corespunzatoare lui P respectiv Q avem |S(P;f)-S(Q;f)|<  .
.
43.A doua teorema de integrare pentru functii de mai
multe variabile
Fie  continua, unde D este o submultime compacta a lui
continua, unde D este o submultime compacta a lui 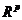 care are frontiera de masura nula.Atunci f este integrabila
pe D.
care are frontiera de masura nula.Atunci f este integrabila
pe D.
44.Teorema de medie pentru integrala multipla
Fie  continua pe D, unde D este o submultime compacta ,conexa si
masurabila a lui
continua pe D, unde D este o submultime compacta ,conexa si
masurabila a lui 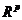 . Atunci exista un punct p in D astfel ca:
. Atunci exista un punct p in D astfel ca:  .
.
45.Teorema de exprimare a unei integrale duble ca o
succesiune de integrale
Daca
f:D->R este o functie continua ,unde exista a,b,c,d  .Atunci:
.Atunci: 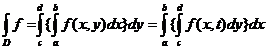 .
.
46.Teorema de schimbare de variabile la integrala
multipla
Fie  de clasa C1 pe G astfel incat
de clasa C1 pe G astfel incat  Daca D este o submultime compacta si masurabila lui G iar
Daca D este o submultime compacta si masurabila lui G iar  este continua, atunci
este continua, atunci  este masurabila si
este masurabila si  .
.
47.Criterii de comparatie pentru integrala improprie
a)Criteriul lui Cauchy : Fie  o functie integrabila Riemann pe [a,c] oricare c>a. Atunci
exista
o functie integrabila Riemann pe [a,c] oricare c>a. Atunci
exista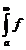 daca si numai daca
daca si numai daca  astfel incat pentru
astfel incat pentru 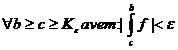 .
.
b)Criteriul de comparatie : Fie 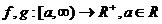 doua functii integrabile Riemann pe [a,c] oricare c>a
astfel incat:
doua functii integrabile Riemann pe [a,c] oricare c>a
astfel incat: . Atunci daca exista
. Atunci daca exista 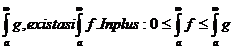 .
.
c)Criteriul de comparatie la limita: Fie  doua functii integrabile Riemann pe [a,c] oricare c>a
astfel incat
doua functii integrabile Riemann pe [a,c] oricare c>a
astfel incat 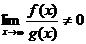 .Atunci integralele improprii
.Atunci integralele improprii  au aceeasi natura(ie.ele exista sau nu simultan)
au aceeasi natura(ie.ele exista sau nu simultan)
48.Criteriul lui Dirichlet pentru integrale
improprii
Fie  ,f functie continua. Presupunem ca exista un numar real M
astfel incat
,f functie continua. Presupunem ca exista un numar real M
astfel incat  ,iar
,iar 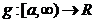 o functie descrescatoare ce tinde catre 0 atunci cand
o functie descrescatoare ce tinde catre 0 atunci cand 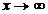 . (ie.
. (ie.  )
)
49.Criteriul lui Cauchy pentru serii
Seria 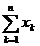 este convergenta daca si numai daca
este convergenta daca si numai daca 
50.Teorema de permutare a seriilor absolut
convergente
Fie 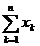 o serie absolut convergenta cu termeni din
o serie absolut convergenta cu termeni din 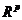 cu suma S. Atunci
pentru orice bijectie
cu suma S. Atunci
pentru orice bijectie  este convergenta si are suma S.
este convergenta si are suma S.
51.Teorema lui Mertens
Fie seriile cu termeni din R:  astfel incat seria
astfel incat seria 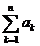 converge absolut catre A, iar
converge absolut catre A, iar  converge catre B. Atunci produsul Cauchy al lor este o serie
convergenta cu suma AB.
converge catre B. Atunci produsul Cauchy al lor este o serie
convergenta cu suma AB.
52.Teorema lui Cesaro
Fie seriile cu termeni din R:  ,iar
,iar  produsul Cauchy al celor doua serii. Daca
produsul Cauchy al celor doua serii. Daca 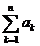 converge catre A,iar
converge catre A,iar  catre B atunci , notand
catre B atunci , notand 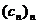 sirul sumelor partiale ale seriei
sirul sumelor partiale ale seriei  avem:
avem:  .
.
53.Criteriile de convergenta pentru serii
1)Criteriul de comparatie : Fie 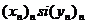 siruri de elemente din
siruri de elemente din  .Daca seria
.Daca seria 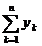 este convergenta atunci si seria
este convergenta atunci si seria 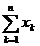 este convergenta.
este convergenta.
2)Criteriul de comparatie la limita: Fie 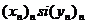 siruri de elemente din
siruri de elemente din  .:
.:
a)Daca exista 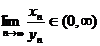 atunci seriile
atunci seriile 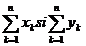 au aceeasi natura.
au aceeasi natura.
b)Daca exista
 si seria
si seria 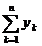 converge atunci si seria
converge atunci si seria 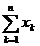 este convergenta. (Criteriul radacinii lui Cauchy).
este convergenta. (Criteriul radacinii lui Cauchy).
3)Criteriul lui Dirichlet : Fie 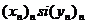 siruri de elemente din
siruri de elemente din  iar
iar 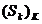 sirul sumelor partiale ale seriei
sirul sumelor partiale ale seriei 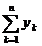 .Presupunem ca
.Presupunem ca 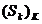 este marginit , sirul
este marginit , sirul  converge catre 0si ca seria
converge catre 0si ca seria  este convergenta .Atunci seria
este convergenta .Atunci seria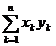 este convergenta.
este convergenta.
4)Criteriul lui Abel
:Fie
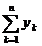 serie convergenta cu elemente din
serie convergenta cu elemente din  iar
iar  sir de elemente din R monoton si convergent. Atunci seria
sir de elemente din R monoton si convergent. Atunci seria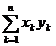 este convergenta.
este convergenta.
54.Teoremele de continuitate,derivabilitate si
integrabilitate pentru serii de functii
1)Teorema de continuitate :Daca  sir de functii continue
sir de functii continue 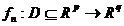 iar seria
iar seria  converge uniform pe D la
converge uniform pe D la 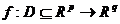 atunci f este continua.
atunci f este continua.
2)Teorema de derivabilitate : Daca  sir de functii derivabile
sir de functii derivabile 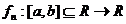 pentru care
pentru care 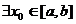 astfel incat seria
astfel incat seria 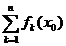 este convergenta iar seria
este convergenta iar seria 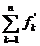 converge uniform. Atunci exista
converge uniform. Atunci exista  astfel incat seria
astfel incat seria  converge uniform catre f si mai mult
converge uniform catre f si mai mult 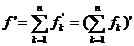 .
.
3)Teorema de integrabilitate: Daca  sir de functii
sir de functii 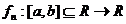 integrabile
Riemann-Stietjes in raport cu
integrabile
Riemann-Stietjes in raport cu  iar seria
iar seria  converge uniform catre
converge uniform catre  .Atunci f este integrabila Riemann-Stieltjes in raport cu g si
.Atunci f este integrabila Riemann-Stieltjes in raport cu g si
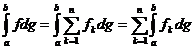
55.Criterii de convergenta pentru serii de functii
Criteriul lui Weierstrass: Daca  sir de functii
sir de functii 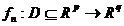 pentru care exista un sir de numere reale
pentru care exista un sir de numere reale 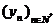 astfel incat pentru orice
astfel incat pentru orice  astfel incat seria
astfel incat seria 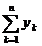 este convergenta.Atunci seria
este convergenta.Atunci seria  converge uniform pe D.
converge uniform pe D.
56.Teorema Cauchy-Hadamard
Daca R-raza de convergenta a seriei de puteri 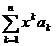 atunci seria este absolut convergenta pentru |x|<R si divergenta
pentru |x|>R.
atunci seria este absolut convergenta pentru |x|<R si divergenta
pentru |x|>R.
57.Teoremele de continuitate ,derivare si integrare
pentru serii de puteri
1)Fie seria 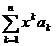 cu raza de convergenta R si S:(-R,R)->R suma seriei de
puteri. Atunci functia S este continua si
cu raza de convergenta R si S:(-R,R)->R suma seriei de
puteri. Atunci functia S este continua si 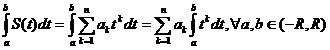 . Mai mult seria de puteri
. Mai mult seria de puteri 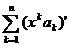 are raza de convergenta R si
are raza de convergenta R si 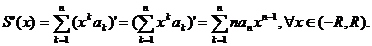
2)Fie R raza de convergenta a seriei de puteri 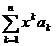 iar K o submultime
compacta a intervalului (-R,R). Atunci seria de puteri
iar K o submultime
compacta a intervalului (-R,R). Atunci seria de puteri 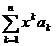 converge uniform pe K.
converge uniform pe K.
58.Teorema de unicitate pentru serii de puteri
????????
59.Teorema lui Bernstein
Fie f:[0,r]->R pentru
care exista derivata de orice ordin.Daca f si derivatele sale de orice ordin
sunt pozitive pentru orice x din [0,r] avem: f(x)= 
60.Teorema lui Abel
Daca seria de puteri 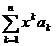 converge pe (-R,R) unde R este raza de convergenta catre
f(x), iar seria
converge pe (-R,R) unde R este raza de convergenta catre
f(x), iar seria converge catre A, atunci seria de puteri
converge catre A, atunci seria de puteri 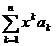 converge uniform pe
[0,R] si
converge uniform pe
[0,R] si 
61.Teorema lui Tauber
Daca seria de puteri 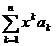 converge pe (-1,1) catre f(x),
converge pe (-1,1) catre f(x),  ,atunci seria
,atunci seria 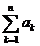 converge la A.
converge la A.


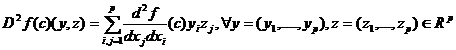 .
. Analog se defineste diferentiala de orice ordin intr-un
punct.
Analog se defineste diferentiala de orice ordin intr-un
punct.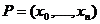 a lui [a,b] are forma
a lui [a,b] are forma 
 )
)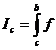 .Definim integrala improprie a lui f pe J=[a,b] ca
fiind
.Definim integrala improprie a lui f pe J=[a,b] ca
fiind 
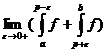 se noteaza cu (CPN)
se noteaza cu (CPN)  Vom spune ca aceasta convergenta este uniforma (in
raport cu
Vom spune ca aceasta convergenta este uniforma (in
raport cu 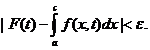 .Definitii similare exista si pentru
.Definitii similare exista si pentru 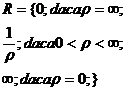 .
.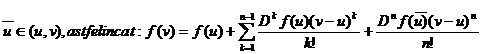 .
. .
.


 daca si numai daca F'=f.
daca si numai daca F'=f.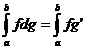 .
.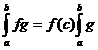 .
.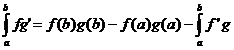 .
. .
.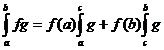 .
.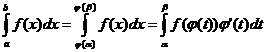 .
. este derivabila si
este derivabila si  .
.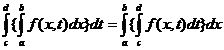 .
. .
.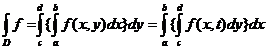 .
.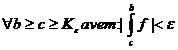 .
.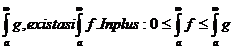 .
. au aceeasi natura(ie.ele exista sau nu simultan)
au aceeasi natura(ie.ele exista sau nu simultan) ,iar
,iar 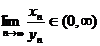 atunci seriile
atunci seriile 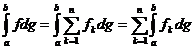
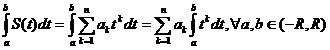 . Mai mult seria de puteri
. Mai mult seria de puteri