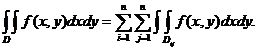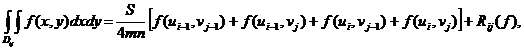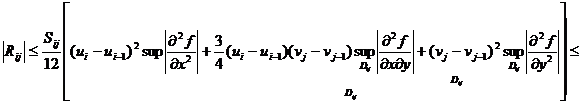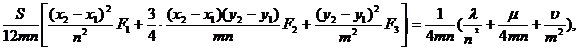Calculul numeric al integralelor multiple
Rezultatele obținute pentru
integralele simple pot fi folosite pentru aproximarea integralelor multiple. In
acest paragraf voi arata cum se aproximeaza integralele duble.
Fie f o funcție reala,
definita și integrabila pe domeniul D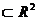 . Pentru calculul integralei
. Pentru calculul integralei
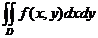 se pot folosi, in
anumite condiții, formulele obținute in cazul integralelor simple.
se pot folosi, in
anumite condiții, formulele obținute in cazul integralelor simple.
De
exemplu, sa presupunem ca domeniul D este delimitat de curbele netede
(netede pe porțiuni) y=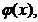 y=
y=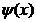 și dreptele x=a, x=b, cu
și dreptele x=a, x=b, cu 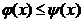 pentru x
pentru x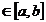 .
.
Daca funcția F: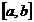
 , definita prin:
, definita prin:
F(x)=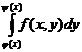 ,
,
este
integrabila pe 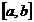 , atunci :
, atunci :
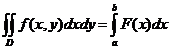
Pentru integrala din membrul drept se
poate folosi o formula de tip Newton:
 , x
, x
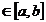 , 0
, 0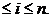
Deoarece F(x )=
)=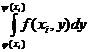 putem folosi din nou o formula de tip Newton.
putem folosi din nou o formula de tip Newton.
Obținem:
F(x )
)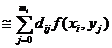 , y
, y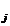
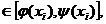
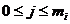 ,
, 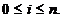
Rezulta in final:
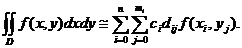
Exemplu. Formula de cubatura de tip Simpson.
Fie D=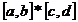 h=
h=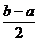 , k=
, k=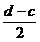 . Avem:
. Avem:
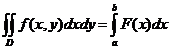 , F(x)=
, F(x)=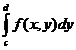
Aplicand formula lui Simpson obținem:
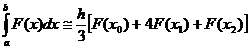
unde: x =a, x
=a, x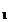
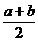 , x
, x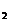 =b.
=b.
Apoi, pentru i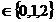 , avem:
, avem:
F(x
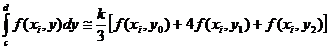
unde: y =c, y
=c, y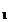
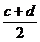 , y
, y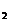 =d.
=d.
Rezulta:
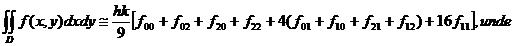
f =f(x
=f(x ,y
,y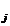 ), i,j
), i,j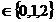
Așadar:
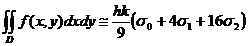
unde:
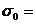 suma valorilor funcției f in
varfurile dreptunghiului D;
suma valorilor funcției f in
varfurile dreptunghiului D;
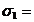 suma valorilor funcției f in mijloacele laturilor lui D;
suma valorilor funcției f in mijloacele laturilor lui D;
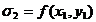 =valoarea in centrul dreptunghiului D.
=valoarea in centrul dreptunghiului D.
Exemplu. Aplicam
formula (43) pentru integrala 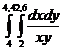 cu h=0,2 și
k=0,3.
cu h=0,2 și
k=0,3.
Valorile
funcției f(x,y)= 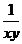 sunt:
sunt:
|
x
y
|
|
|
|
|
|
|
|
Rezulta
:
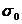 =0,125+0,096154+0,0874126+0,113636=0,4222026
=0,125+0,096154+0,0874126+0,113636=0,4222026
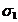 =0,108696+0,0915751+0,0988142+0,119048=0,4181333
=0,108696+0,0915751+0,0988142+0,119048=0,4181333
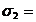 0,103520
0,103520
Deci:
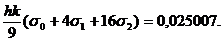
Valoarea
exacta este:
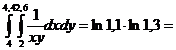 0,0250059.
0,0250059.
Daca
dimensiunile dreptunghiului D sunt mari, pentru ameliorarea preciziei se divide
dreptunghiul D intr-un numar oarecare de dreptunghiuri  . Pe fiecare D
. Pe fiecare D se aplica o formula de tipul (43), dupa care se
insumeaza rezultatele obținute.
se aplica o formula de tipul (43), dupa care se
insumeaza rezultatele obținute.
Fie h= , k=
, k= , x
, x =a+ih,
=a+ih,  , (x
, (x =a, x
=a, x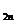 =b),
=b),
y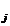 =y
=y +jk,
+jk, 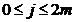 , (y
, (y =c, y
=c, y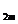 =d).
=d).
Vom nota
f =f(x
=f(x ,y
,y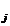 ), D
), D
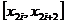
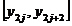
Din (43) rezulta:
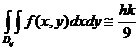

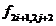 +
+

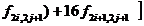 .
.
Deoarece:
 ,
,
se
obține in final:
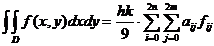 , unde a
, unde a sunt elementele matricei:
sunt elementele matricei:
A=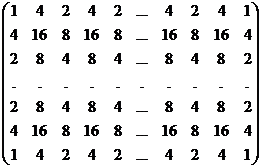
Daca domeniul de integrare D este
oarecare (marginit), atunci se construiește un dreptunghi 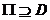 și se definește
funcția f
și se definește
funcția f
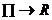 astfel:
astfel:
f (x,y)=
(x,y)=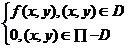
Avem : 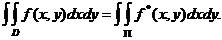
Pentru
integrala din membrul drept se poate folosi o formula de tipul (44).
In
continuare vom studia doua tipuri de formule de aproximare a integralelor
duble, numite și formule de cubatura.
1 Formule de cubatura
pe triunghi.
Fie ABC-
un triunghi oarecare. Centrul de greutate al punctelor materiale A,B,C se
numește baricentrul triunghiului ABC.
Notam:
L-baricentrul triunghiului ABC care
are in A,B,C masele 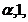 respectiv 1 unitați de
masa;
respectiv 1 unitați de
masa;
M-baricentrul triunghiului ABC care
are in A,B,C masele 1,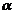 , respectiv 1 unitați de masa;
, respectiv 1 unitați de masa;
N-baricentrul triunghiului ABC care
are in A,B,C masele 1,1, respectiv 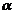 unitați de masa;
unitați de masa;
Se știe ca L,M,N se
afla pe medianele A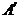
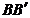 respectiv
respectiv 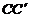 . In cazul
. In cazul 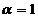 cele trei baricentre coincid cu centrul de greutate al triunghiului ABC.
cele trei baricentre coincid cu centrul de greutate al triunghiului ABC.
Fie A(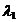
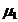 ), B(
), B(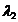
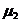 ), C(
), C(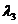
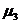 ). Rezulta:
). Rezulta:
L(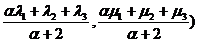 , M(
, M(
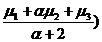
N(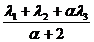
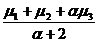
In general, vom nota cu L ,M
,M , N
, N baricentrele triunghiului ABC corespunzatoare parametrelor
baricentrele triunghiului ABC corespunzatoare parametrelor 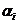
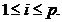
Vom
determina 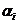 ,c
,c
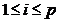 , astfel incat formula:
, astfel incat formula:
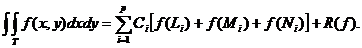
sa aiba ordinul de exactitate p, oricare ar fi
triunghiul ABC.
S-a notat cu T domeniul delimitat de triunghiul ABC.
Sunt adevarate urmatoarele doua
propoziții:
Propoziția
1. Daca pentru o anumita alegere
a parametrilor 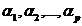 și a
coeficienților c
și a
coeficienților c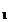 ,c
,c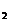 ,,c
,,c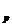 se obține R(f)=0 in (45) pentru f(x,y)=x
se obține R(f)=0 in (45) pentru f(x,y)=x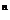 , atunci R(f)=0 pentru orice polinom in doua variabile
f, de grad mai mic sau egal cu n.
, atunci R(f)=0 pentru orice polinom in doua variabile
f, de grad mai mic sau egal cu n.
Propoziția
2. Daca p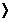 5, nu exista parametrii
5, nu exista parametrii 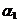 ,
,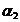 ,,
,,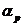 și coeficienții c
și coeficienții c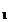 ,c
,c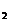 ,,c
,,c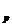 , astfel incat formula de cubatura(45) sa fie
exacta pentru f(x,y)=x
, astfel incat formula de cubatura(45) sa fie
exacta pentru f(x,y)=x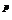 .
.
Cazuri
particulare.
I. p=1.
In acest caz se determina
formula:
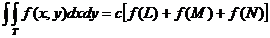 +R(f) ,
+R(f) ,
care are
proprietatea: R(x)=0.
Daca S este aria triunghiului
ABC, atunci:
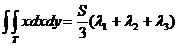
Pentru f(x,y)=x avem:
f(L)=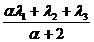
f(M)=
f(N)=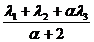
Rezulta: f(L)+f(M)+f(N)=
Deci: c=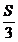
Se obține formula:
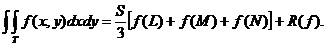
Pentru 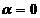 avem:
avem:
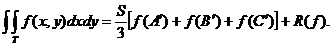
unde 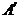 ,
,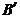 ,
,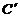 sunt mijloacele laturilor triunghiului ABC:
sunt mijloacele laturilor triunghiului ABC:
Pentru 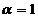 avem:
avem:
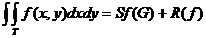
unde G este centrul de greutate al triunghiului ABC.
Pentru 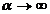 avem:
avem:
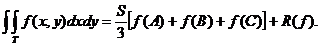
II. p=2. In acest caz se determina formula:
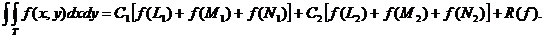
cu c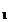 și c
și c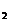 astfel incat R(
astfel incat R( )=0.
)=0.
Se obține:
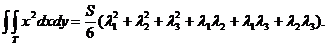
Pentru
f(x,y) =x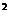 avem:
avem:
f(L )+f(M
)+f(M )+f(N
)+f(N )=
)=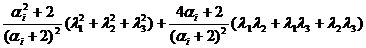 , i=1,2.
, i=1,2.
Prin identificare obținem:
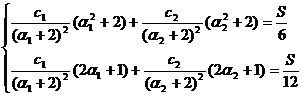
Daca se aleg 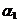
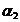 astfel incat determinantul acestui sistem sa fie nenul, se obține
soluția:
astfel incat determinantul acestui sistem sa fie nenul, se obține
soluția:
c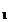
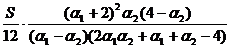
c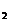
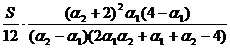
Pentru 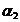 =1 condiția de rezolvare este
=1 condiția de rezolvare este 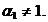 In acest caz coeficienții
In acest caz coeficienții 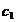
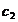 sunt:
sunt:
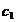
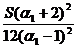
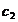
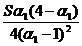
Se
obține formula:
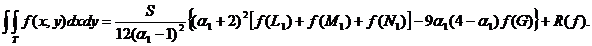
Pentru  avem:
avem:
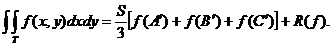
Pentru 
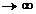 avem:
avem:
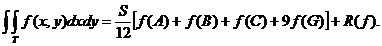
Pentru 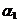 =4 avem:
=4 avem:

Unde L, M, N sunt mijloacele segmentelor GA, GB,
respectiv GC.
2. Formule de cubatura
pe dreptunghi.
Fie formula:
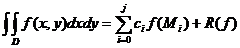
unde D=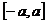

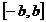
Avem:
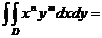 0, daca n este impar sau m este
impar,
0, daca n este impar sau m este
impar,
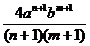 , daca m și n sunt numere pare.
, daca m și n sunt numere pare.
Fie p ordinul de exactitate al
formulei (48), adica R(x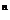 y
y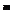 )=0 pentru m+n
)=0 pentru m+n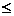 p.
p.
Din (48) și (49) rezulta:
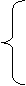
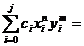 0, daca n este impar sau m este
impar,
0, daca n este impar sau m este
impar,
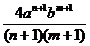 , daca m și n sunt numere pare.
, daca m și n sunt numere pare.
Pentru p=0 avem n=m=0. Din (50) rezulta:
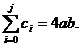
Se considera un singur nod M (x
(x ,y
,y ). Rezulta c
). Rezulta c =4ab.
=4ab.
Se
obține formula:
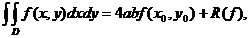 (x
(x ,y
,y
 D.
D.
Pentru p=1 se considera cazurile:
(m,n)= (0,0), (m,n)=(1,0), (m,n)=(0,1).
Din (50)
rezulta:
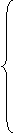
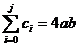
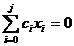
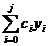 =0
=0
Se ia tot un nod M (x
(x ,y
,y ). Din (52) rezulta:
). Din (52) rezulta:
c =4ab, x
=4ab, x =0, y
=0, y
Rezulta formula:
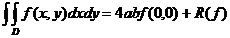
care are ordinul de exactitate unu.
Numarul
ecuațiilor și necunoscutelor din sistemul (50) poate fi
micșorat. Pentru aceasta se
procedeaza astfel:
a) Daca numarul
nodurilor este impar, se convine ca nodul M (x
(x ,y
,y ) sa fie M
) sa fie M (0,0) cu coeficientul c
(0,0) cu coeficientul c =4ab
=4ab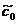
b) Daca numarul nodurilor
este par, atunci se adauga formal nodul M (0,0) cu coeficientul c
(0,0) cu coeficientul c =4ab
=4ab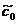
In ambele cazuri avem nodurile:
M , M
, M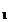 ,,M
,,M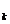 ,M
,M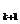 ,,M
,,M , (j=2k).
, (j=2k).
Vom lua:
c =c
=c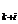 =2ab
=2ab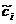
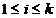
x =-x
=-x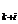 =a
=a
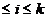
y =-y
=-y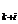 =b
=b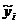
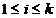
Pentru
n+m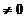 rezulta:
rezulta:
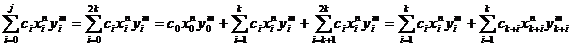 =
=
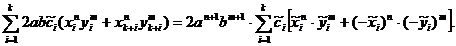
Daca n+m este numar impar
atunci:
a) n este numar par, iar m
este numar impar
sau:
b) n este numar impar, iar m
este numar par.
In ambele cazuri: 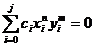
In acest caz ecuațiile sistemului
(50) sunt verificate.
Daca n+m este numar par
atunci:
a)
n,m sunt numere impare
sau:
b)
n,m sunt numere pare.
In ambele cazuri:

Pentru f(x,y)=1 (n=m=0), din (48)
rezulta:
4ab=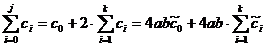
Deci : 
Sistemul (50) devine:
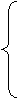
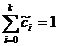
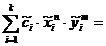 0, n
impar (m impar)
0, n
impar (m impar)
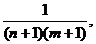 n par (m par), m+n
n par (m par), m+n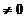
Cazuri particulare. I. p=3, j=3 (patru noduri).
In acest caz 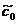 =0. Ecuațiile (54) se scriu pentru m+n=0 și m+n=2. Avem cazurile:
=0. Ecuațiile (54) se scriu pentru m+n=0 și m+n=2. Avem cazurile:
(m,n)=(0,0), (m,n)=(0,2), (m,n)=(2,0), (m,n)=(1,1).
Rezulta
sistemul:
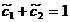
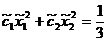
 +
+ =
=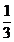
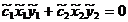
Acest sistem este compatibil, dublu
nedeterminat. Soluția sa este :
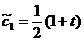

 cos
cos 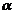 ,
,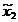
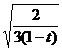 .sin
.sin 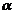
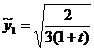 .sin
.sin 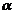
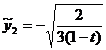 . cos
. cos 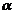
Avem:
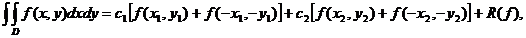
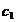 =2ab
=2ab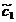 =ab(1+t),
=ab(1+t),
c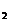 =2ab
=2ab =ab(1-t).
=ab(1-t).
Se obține formula:
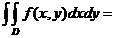
=ab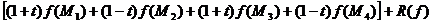
M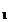 (a
(a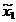 ,b
,b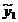 ), M
), M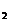 (a
(a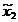 ,b
,b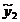 ), M
), M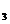 (-a
(-a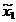 ,-b
,-b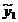 ), M
), M (-a
(-a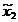 ,-b
,-b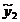 ).
).
Pentru t=0, 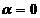 avem:
avem:
M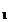 (a
(a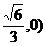 , M
, M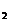 (0,-b
(0,-b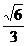 ), M
), M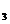 (-a
(-a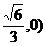 , M
, M (0,b
(0,b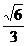
Rezulta formula:

Pentru t=0 și 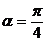 avem:
avem:
x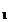
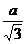
 , y
, y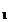
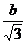 =-y
=-y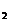
Rezulta formula:
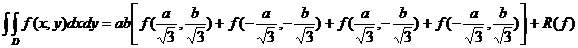
II. p=3, j=4 (cinci noduri).
Sistemul (54) devine:
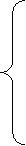
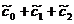 =1
=1
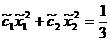
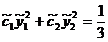
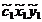
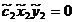
Acest sistem este compatibil, triplu
nedeterminat. Soluția sa este :
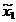
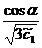
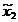
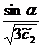
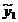
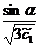
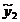
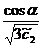
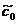
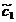

Se obține formula:
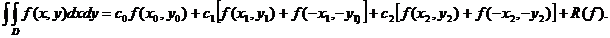
Pentru 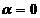 și
și 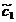

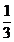 rezulta
rezulta 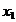 =a, x
=a, x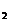

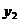 =-b. Se obține formula:
=-b. Se obține formula:
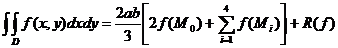
M
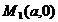
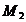 (-a,0),
(-a,0), 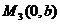
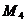 (0,-b).
(0,-b).
Pentru 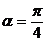
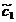

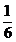 se obține formula:
se obține formula:
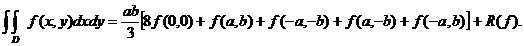
3. Formule de cubatura
cu rest dat.
Fie 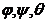 :D=
:D=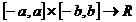 astfel incat:
astfel incat:
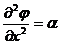 ,
, 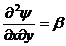 ,
,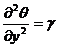
și f:D , f
, f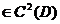
Avem:

=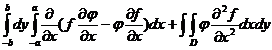
Deci:

Analog:
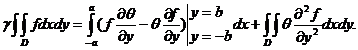
Apoi:
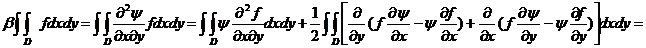 =
=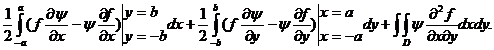
Rezulta:
(57.3)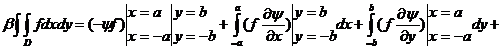
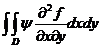
Deoarece 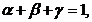 dupa adunarea
relațiilor (57.1), (57.2) și (57.3), obținem:
dupa adunarea
relațiilor (57.1), (57.2) și (57.3), obținem:
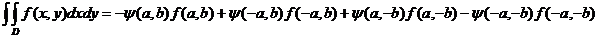
+ 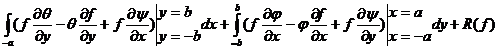
unde:
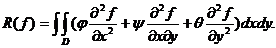
Vom determina funcțiile 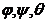 astfel incat
integralele simple sa fie nule. Punem condițiile:
astfel incat
integralele simple sa fie nule. Punem condițiile:
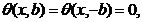

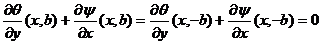 ,
,
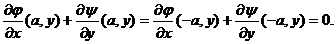
Rezulta:
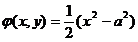
 c=const.
c=const.
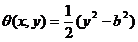
Se obține formula:
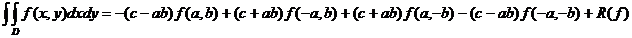 unde :
unde :
R(f)=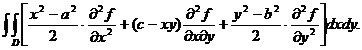
Formula (59) este de tipul:
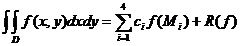 ,
,
unde 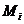 ,
, 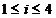 , sunt varfurile dreptunghiului D.
, sunt varfurile dreptunghiului D.
Studiul
restului. Restul este:
R(f)=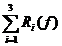 ,
,
unde:
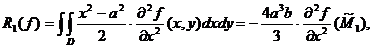
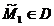 ,
,
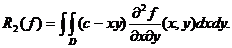
Daca 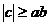 atunci
atunci 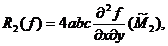
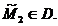
Daca 
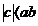 , atunci
, atunci 
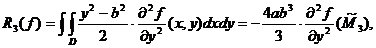
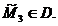
Cazuri particulare. I. Pentru c=-ab obținem:
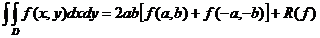 ,
,
unde:
R(f)=- 
II.
Pentru c=ab obținem:
(63) 
unde:
R(f)=-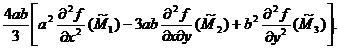
III. Pentru c=0
obținem:

unde:
R(f)=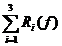 ,
,

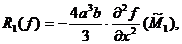
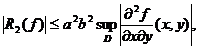
R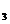 (f)=-
(f)=-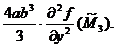
Fie acum D=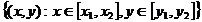 . Notam cu
. Notam cu 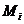
 , varfurile lui D, S=(x
, varfurile lui D, S=(x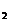 -x
-x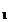 )(y
)(y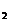 -y
-y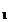

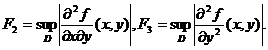
Efectuam
schimbarea de variabila:
x=

y=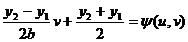 v
v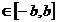
Obținem:
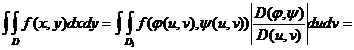
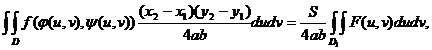 unde:
unde:
F(u,v)=f(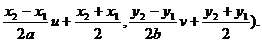
Pentru integrala 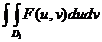 folosim una din
formulele anterioare. De exemplu, aplicand (65) obținem:
folosim una din
formulele anterioare. De exemplu, aplicand (65) obținem:

Dar:
F(a,b)+F(-a,b)+F(a,-b)+F(-a,-b)=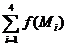 ,
,
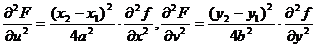 ,
,
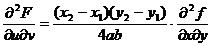 ,
,
Rezulta:
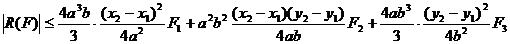 .
.
Deci:

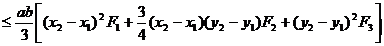
Se obține formula:
(69) 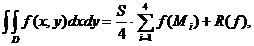 R(f)=
R(f)=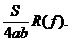
Din (68) rezulta:

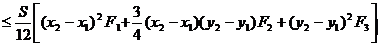
Fie acum
o diviziune a dreptunghiului D astfel:
D=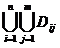 , D
, D =
=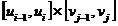 ,
,
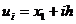 , h=
, h=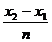 ,
, 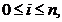
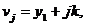 k=
k= ,
, 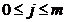 .
.
S =(
=(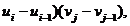 f
f =f(
=f(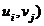 ,
, 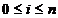 ,
, 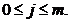
Avem  și:
și:
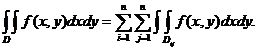
Din (69) rezulta:
(71) 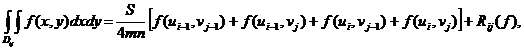
iar din
(70) deducem:
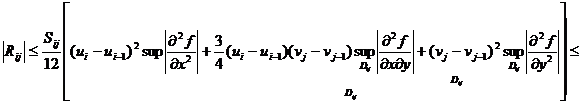
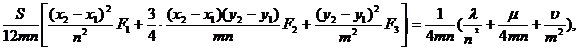
unde:
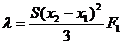

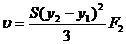
Deci:
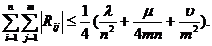
Obținem formula:
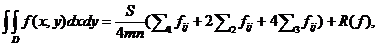
unde:
 este suma valorilor funcției f in varfurile
dreptunghiului D;
este suma valorilor funcției f in varfurile
dreptunghiului D;
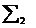 este suma valorilor funcției f in nodurile situate in
interiorul laturilor dreptunghiului D;
este suma valorilor funcției f in nodurile situate in
interiorul laturilor dreptunghiului D;
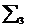 este suma valorilor funcției f in nodurile interioare
dreptunghiului D;
este suma valorilor funcției f in nodurile interioare
dreptunghiului D;
(74) 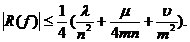
Pentru aproximarea integralei cu
eroarea 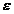 , numerele m și n se aleg astfel incat:
, numerele m și n se aleg astfel incat:
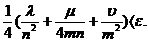
Algoritmi asemanatori se
obțin folosind și alte tipuri de formule de cubatura.


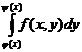 ,
,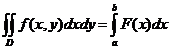
 , x
, x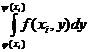 putem folosi din nou o formula de tip
putem folosi din nou o formula de tip 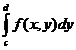
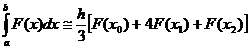
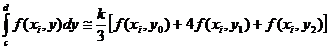
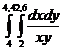 cu h=0,2 și
k=0,3.
cu h=0,2 și
k=0,3.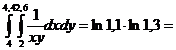 0,0250059.
0,0250059.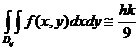
 ,
,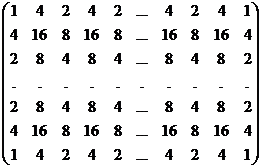
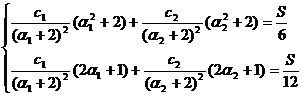

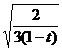
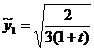
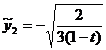


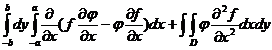

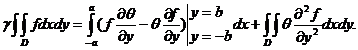
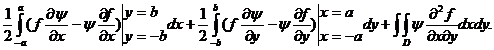
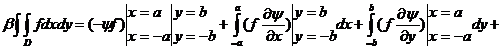
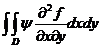
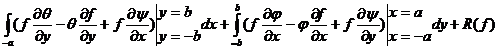
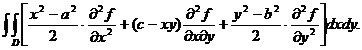


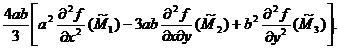
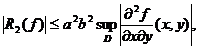

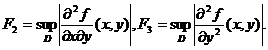
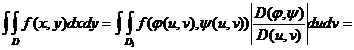
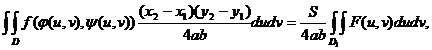 unde:
unde: