Despre sirul lui Fibonacci
Cine a fost Fibonacci ?
Fibonacci a fost unul dintre cei mai mari matematicieni ai
Evului Mediu. Nascut ȋn Italia, ȋn 1175, a fost educat ȋn
Nordul Africii, unde tatal sau detinea un post diplomatic.
In 1202 revine ȋn Italia si publica
un tratat de aritmetica si algebra intitulat " Liber abaci " . In acest tratat
introduce pentru prima data ȋn Europa sistemul de numeratie
pozitional arab. De asemenea, in1220 publica " Practica geometriae " , un
compendiu de rezultate din geometrie si trigonometrie, iar in 1225 " Liber
quadratorum", in care studia calculul radicalilor cubici.
Totusi, Fibonacci a ramas ȋn
memoria noastra prin binecunoscutul sir Fibonacci:
0,
1, 1, 2, 3, 5, 8, 13, .
Sirul respectiv a fost introdus de catre
Fibonacci in anul 1202, atunci matematicianul fiind sub numele de Leonardo
Pisano ( Leonard din Pisa). Mai tarziu
matematicianul insusi si-a spus Leonardus filius Bonacii Pisanus ( Leonard
fiul lui Bonaccio Pisanul). In secolul XIV sirul prezentat mai sus a fost
denumit sirul lui Fibonacci prin contractia cuvintelor filius
Bonacii.
Sirul de mai sus apare ȋn cartea pomenita
anterior " Liber abaci ", fiind utilizat
ȋn rezolvarea unei probleme de . matematica.
Cum si unde a fost
folosit pentru prima oara sirul lui Fibonacci? - PROBLEMA IEPURILOR
Se pare ca si pe vremea lui Fibonacci se
organizau concursuri de matematica. In Pisa, a participat si
Fibonacci la un astfel de concurs care a fost condus de insusi ȋmparatul
Frederik al II-lea. Problema propusa concurentilor suna astfel:
Problema
iepurilor
Fie data o pereche de iepuri. Se
stie ca fiecare pereche de iepuri produce ȋn fiecare luna o
noua pereche de iepuri, care la randul sau devine productiva la
varsta de o luna. Sa se determine cate perechi de iepuri vor fi dupa n
luni.
Pentru inceput vom remarca istoria
acestei probleme si apoi solutia ei, precum si alte probleme ce
tin de ea.
Vorbind de matematica din antichitate
fiecare ar denumi cativa reprezentanti ca Euclide, Pytagoras, Heron s.a. Unul dintre
cei mai ilustri matematicieni ai Evului Mediu, contemporan cu Viete, ar fi
Leonardo din Pisa, cunoscut sub numele Fibonacci (prescurtare de la filus
Bonacci, adica fiul lui Bonacci).
Tratatul 'Liber abaci'
contine aproape toata informatia acelui timp, referitoare la
aritmetica si algebra, si care a avut un rol important pe
parcursul urmatoarelor secole ȋn dezvoltarea matematicii in Europa. In
particular, in baza acestui tratat, europenii au luat cunostinta de
scrierea arabica a numerelor, adica de sistemul de numeratie pozitional
arab. La fel, ȋn 1220 publica 'Practica geometrica', in
1225 'Liber quadratorum'. Tratatul 'Liber abaci' a fost
reeditat ȋn 1228. Una din problemele discutate ȋn 'Liber
abaci' este anume 'problema iepurilor', (p. 123-124 ȋn
editia anului 1228) prezentata la inceputul
acestui material.
Rezolvarea acestei probleme.
Fie fn numarul
de perechi de iepuri dupa n luni. Numarul de perechi de iepuri
dupa n + 1, notat prin fn+1, va fi
numarul de perechi la luna n, adica fn, plus
numarul de iepuri nou-nascuti. Cum iepurii se nasc din pereche de
iepuri cu varsta mai mare de o luna, iepurii nou-nascuti vor fi fn-1
perechi.
Prin urmare se obtine relatia
In plus,
Prin urmare am obtinut un sir numeric definit in
mod recurent. Scriind termenii acestui sir,
determinam
numit sirul Fibonacci. Fiecare
termen al sirului, incepand cu al treilea, este egal cu suma
precedentilor doi termeni. Primii doi termeni se considera fiind
dati, f0 = 0, f1 = 1.
Astfel 'problema iepurilor'
s-a redus la rezolvarea ecuatiei functionale ( ), adica la
determinarea termenului general fn a sirului, care
verifica relatia ( ) in conditiile
(
Presupunem ca sirul fn
are forma
unde l este un parametru real.
Substituind
fn
ȋn ( ),
obtinem
ln ln ln
sau echivalent
ln l l
Cum fn n I N ),
ultima egalitate devine
care reprezinta o ecuatie de gradul doi ȋn
raport cu parametrul real l Din ( ) deducem
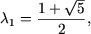

Asadar,
sirurile
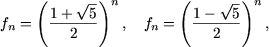
verifica egalitatea ( ). De aici, deducem
ca ecuatia ( ) poseda
mai multe solutii. Ȋn general exista o infinitate de siruri
care verifica relatia ( ). Sirul de
forma
unde c1, c2 sunt
constante reale fixate, de asemenea verifica relatia ( ). Mai mult, se
poate arata ca orice sir ce verifica egalitatea ( ) are forma (
Sirul Fibonacci se determina
univoc, si unicitatea este dictata de primii doi termeni, adica
de conditiile initiale ( Substituind n = 0 si
n = 1 ȋn ( ), se obtine
sistemul liniar

cu
solutia 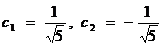 .
.
In final, termenul de rang n al sirului
Fibonacci are forma
Proprietati
ale sirului lui Fibonacci
|
1.
f1 + f2
+ + fn = fn+2 - 1.
|
|
Demonstratie.
|
f = f3 - f2
|
|
f = f4 - f3
|
|
|
fn = fn+1 - fn
|
|
fn = fn+2 - fn+1.
|
Insumand parte cu parte
egalitatile anterioare se obtine
f + f2
+ + fn = fn+2 - f2,
si cum f2 = 1 se obtine egalitatea
(
2. f1
+ f3 + f5 + + f2n-1
= f2n.
3 . f2 + f4
+ + f2n = f2n+1 - 1.
Proprietatile 2 - 3 se
demonstreaza similar cu 1.
|
4. f12
+ f22 + + fn2 =
fn · fn+1.
|
|
Demonstratie. Se
observa cu usurinta ca re loc relatia
fn·fn+1
- fn-1fn = fn(fn+1
- fn-1) = fn2
(n I N*)
Din aceasta relatie, deducem egaliatile
|
f = f1·f2,
|
|
f = f2·f3 - f1·f2,
|
|
f = f3·f4 - f2·f3,
|
|
|
fn = fn·fn+1
- fn-1·fn.
|
Insumand parte cu parte egalitatile precedente
se obtine egalitatea (
|
5. Sa se arate ca fn+m
= fn-1 · fm
+ fn · fm+1,
|
|
unde fn reprezinta
termenul de rang n al sirului Fibonacci.
Demonstratie.
Vom demonstra
( ) utilizand metoda
inductiei matematice. Vom face inductia dupa m I N.
Pentru m = 1, egalitatea ( ) devine
fn = fn-1·f1
+ fn·f2,
care este echivalenta cu fn+1
= fn-1 + fn . (adevarat)
Pentru m =
2 formula ( ) la fel este
evidenta. Intr-adevar,
fn = fn-1f2
+ fnf3 = fn-1 + 2fn
= fn-1 + fn + fn
= fn+1 + fn.
Astfel baza inductiei este
verificata (m = 1; m = 2). Presupunem ca ( ) este
adevarata pentru m = k si m = k + 1
si vom demonstra ca este adevarata si pentru m = k
+ 2.
Asadar, presupunand ca sunt adevarate
egalitatile
|
fn+k = fn-1fk
+ fnfk+1,
|
|
fn+k+1 = fn-1fk+1
+ fnfk+2.
|
Insumand parte cu parte ultimele egalitati, se
obtine
fn+k+2 = fn-1·fk+2
+ fn·fk+3,
care
reprezinta egalitatea ( )
pentru m = k + 2.
6. f2n = fn-1fn
+ fn·fn+1.
Egalitatea rezulta din ( ) punand m
= n.
7. Termenul f2n
se divide prin fn.
Demonstratie. Din
6 rezulta
f2n = fn(fn-1
+ fn+1),
de unde rezulta ca f2n este divizibil cu fn.

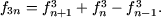
Proprietatile
8 - 9 sunt consecinte directe ale egalale egalitatii 6.
|
10. fn2
= fn-1fn+1 + (-1)n+1
|
|
Demonstratie. Vom
demonstra egalitatea ( ) prin
inductie dupa n.
Pentru n = 2 egalitatea ( ) devine
f = f1·f3
- 1,
care este adevarata.
Presupunem ca ( ) este
adevarata pentru n si vom demonstra ca este adevarata
si pentru n + 1. Presupunem ca are loc egalitatea
fn = fn-1·fn+1
+ (-1)n+1.
Adunam la ambele parti ale ultimei
egalitati fn·fn+1. Ca
rezultat se obtine
fn + fn·fn+1
= fn-1·fn+1 + fn·fn+1
+ (-1)n+1,
sau
echivalent
fn(fn + fn+1)
= fn+1(fn-1 + fn)
+ (-1)n+1,
si
cum fn+2 = fn + fn+1
(a se vedea definitia sirului Fibonacci) deducem
fnfn = fn+12
+ (-1)n+1,
sau
fn = fn·fn+2
+ (-1)n+2.
Deci ( ) este
adevarata si pentru n + 1.
11. Sa se arate ca daca n este
divizibil cu m atunci fn este divizibil prin fm.
Demonstratie. Fie
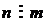 , adica n
= mk. Vom demonstra proprietatea ( ) prin
inductie dupa k. Pentru k = 1, n = m, si
deci, fn evident este divizibil prin fm.
Presupunem ca fmk este divizibil prin fm.
Sa examinam fm(k+1). Cum fm(k+1)
= fmk+m si utilizand egalitatea (10) se obtine
, adica n
= mk. Vom demonstra proprietatea ( ) prin
inductie dupa k. Pentru k = 1, n = m, si
deci, fn evident este divizibil prin fm.
Presupunem ca fmk este divizibil prin fm.
Sa examinam fm(k+1). Cum fm(k+1)
= fmk+m si utilizand egalitatea (10) se obtine
fm(k+1) = fmk-1fm
+ fmk·fm+1.
Primul termen al sumei din dreapta evident este divizibil
prin fm. Termenul al doilea este divizibil prin fm
conform presupunerii inductive. Prin urmare suma acestor termeni este divizibila
prin fm, si deci 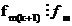 . Proprietatea 11 este demonstrata.
. Proprietatea 11 este demonstrata.
Eminescu
si sirul lui Fibonnaci
Daca luam trei termeni consecutivi
din sirul Fibonacci (de exemplu 1, 2, 3) si ii vom numi "ieri",
"azi", "maine". Relatia dintre termeni este:
"maine" - "ieri" = "azi"
Sa retinem acest lucru!
Dar care este legatura dintre Mihai Eminescu si acest
sir?
Intr-una dintre poeziile sale acesta spune:
"Cu mane
zilele-ti adaogi,
Cu ieri
viata ta o scazi
Si ai cu
toate astea-n fata
De-a pururi ziua
cea de azi."
(Cu mane zilele-ti adaogi - M. Eminescu)
Observam ca primele doua versuri reprezinta
diferenta dintre "maine" si "ieri".
Al treilea vers da semnul egal, iar versul al
patrulea este tocmai "azi
Despre "Sectiunea de aur"
Problema inmultirii
iepurilor este departe de a fi realista, chiar daca a dus la o
descoperire atat de importanta cum este acest sir. Dar cunoscutul
sir al lui Fibonacci, generat de aceasta problema, are numeroase
aplicatii, deosebit de interesante. Unul dintre cele mai importante
aspecte este legatura dintre numerele Fibonacci si sectiunea
de aur.
Sectiunea de aur este
probabil unul dintre cele mai misterioase numere, constituind de secole o
fascinatie pentru matematicieni si artisti. Ca si numerele
irationale 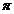 sau
sau 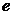 , pare a face parte
din "constitutia" Universului, sectiunea
de aur regasindu-se sistematic ȋn lumea vie. De exemplu, o
regasim in modul de dispunere a frunzelor, petalelor sau semintelor
la plante, in raportul dintre diferite parti ale corpului omenesc,
etc .
, pare a face parte
din "constitutia" Universului, sectiunea
de aur regasindu-se sistematic ȋn lumea vie. De exemplu, o
regasim in modul de dispunere a frunzelor, petalelor sau semintelor
la plante, in raportul dintre diferite parti ale corpului omenesc,
etc .
Acest numar a fost
cunoscut si studiat inca din antichitate, sculptura si
arhitectura Greciei antice din secolul lui Pericle respectand cu rigurozitate
sectiunea de aur, aceasta fiind considerata o masura a armoniei
si echilibrului.
Marea reputatie a lui
Fibonacci a facut ca imparatul Germaniei Frederic II sa vina
ȋn 1225 la Pisa, ȋnsotit de un grup de matematicieni, care
doreau sa il supuna pe Fibonacci la un examen public. Una din
problemele date spre rezolvare a fost:
-sa se gaseasca un patrat
perfect , care ramane patrat perfect daca este marit sau micsorat
cu 5. Dupa un timp de gandire , Fibonacci a gasit numarul
cautat. Era fractia: 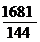 sau
sau 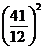 .
.
Intr-adevar:
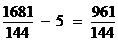 si
si 
Sau  si
si 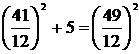
Nu cunoastem rationamentul lui
Fibonacci , dar problema a fost rezolvata ȋn mod stralucit.
Oare nu cumva Fibonacci a plecat
de la reprezentarea geometrica a oricarui patrat perfect ca suma
unor numere impare ordinale?
Pornind de la aceasta ipoteza,
Viaceslav Nezabutkin a gasit o solutie originala a problemei lui
Fibonacci, care este interesanta tocmai prin faptul ca se apropie de
metodele folosite pe timpul lui Fibonacci.
Secventa numerelor lui Fibonacci a
fascinat de-a lungul istoriei pe foarte multi oameni de stiinta,
matematicieni, fizicieni, biologi si continua sa o faca
chiar si ȋn prezent.
Fibonacci
si natura
Plantele nu au cum sa
cunoasca numerele lui Fibonacci, dar ele se dezvolta in cel mai
eficient mod. Astfel, multe plante au aranjamentul frunzelor dispus intr-o
secventa Fibonacci in jurul tulpinei. Anumite conuri de pin
respecta o dispunere data de numerele lui Fibonacci, si de
asemenea aranjarea semintelor de floarea soarelui. Inelele de pe trunchiurile
palmierilor respecta numerele lui Fibonacci. Motivul pentru toate acestea
este realizarea unui optim, a unei eficiente maxime. Astfel de exemplu, urmand
secventa lui Fibonacci, frunzele unor plante pot fi dispuse astfel
ȋncat sa ocupe un cat mai mic spatiu si sa
obtina cat mai multa lumina de la soare.
Ideea dispunerii frunzelor ȋn
acest mod pleaca de la considerarea unghiului de aur de 222, 5
grade, unghi care impartit la ȋntregul 360 de grade va da ca rezultat
cifra
0.61803398, cunoscuta ca ratia sirului lui Fibonacci.

Cu alte
cuvinte, numarul petalelor florilor este de cele mai multe ori, un
numar al secventei Fibonacci:
iris, crin: 3 petale
trandafir salbatic, viorele, lalele, majoritatea florilor: 5 petale
margaretele pot avea 34 de petale sau 21 de petale pentru cele mai
soiuri
si exemplele sunt nenumarate.
Cochilia
melcului
Cati
dintre noi nu au studiat un pic cochilia melcilor iesiti 'la
plimbare' dupa o ploaie de vara. Designul ei urmeaza o
spirala extrem de reusita, o spirala pe care noua
ne-ar fi greu sa o realizam trasand-o cu pixul. Fiind studiata
mai in amanuntime, s-a ajuns la concluzia ca aceasta spirala
urmareste dimensiunile date de secventa lui Fibonacci:
pe axa pozitiva: 1, 2, 5, 13, samd
pe axa negativa: 0, 1, 3, 8, samd..
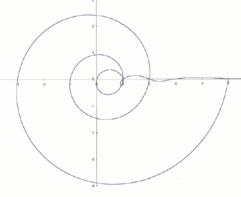

Dupa cum putem observa, aceste 2 subsiruri combinate, vor da chiar
numerele lui Fibonacci.
Ratiunea
si motivatia pentru aceasta dispunere este simpla: in acest
fel cochilia ii creaza melcului, in interior un maxim de spatiu
si de siguranta. Este inca unul din nenumaratele exemple de
aplicare a secventei in natura.
Corpul uman
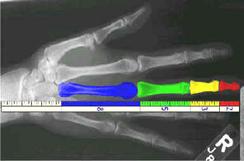
Mana umana
are 5 degete, fiecare deget avand 3 falange separate prin 2 incheieturi (numere
in secventa). In medie, dimensiunile falangelor sunt:
2cm, 3cm, 5cm. In continuarea lor este un os al palmei care are in medie 8 cm.
Fata
umana este caracterizata, din punct de vedere estetic prin cateva dimensiuni
principale: distanta intre ochi, distanta dintre gura si ochi
si distanta dintre nas si ochi, dimensiunea gurii. In
stiinta esteticii se apreciaza ca fata este cu atat considerata
mai placuta ochiului cu cat aceste dimensiuni respecta mai bine
secventa lui Fibonacci.
Numerele lui Fibonacci sunt
considerate a fi, de fapt, sistemul de numarare al naturii, un mod de
masurare al Divinitatii. Aceste numere apar peste tot in natura,
pornind de la aranjamentul frunzelor, de la sabloanele petalelor unei
flori si ajungand la falangele mainii umane. Descrierile si pozele prezentate
pot fi argumente ale acestor afirmatii, marturii ale acestei fascinante
secvente a numerelor lui Fibonacci.



 si
si