Distributii de
probabilitate

Distributii de probabilitate discrete - Variabila
discreta este acea variabila care ia ca valori numai numere
intregi. O variabila este variabila aleatoare discreta daca
sunt cunoscute probabilitatile de aparitie pentru fiecare dintre
valorile posibile.
In Excel exista functii care rezolva
diverse chestiuni legate de distributiile de probabilitate:
binomiala, Poisson, hypergeometrica.
Distributia de
probabilitate binomiala
Modelul legii binomiale - Se repeta un experiment de
n ori. Rezultatele posibile sunt exces si esec. Probabilitatea
succesului este p<n si probabilitatea esecului este q=1-p. Cele n
incercari sunt independente una de alta.
Numarul de succese obtinute
din cele n incercari repetate este o variabila aleatoare de tip
binomial care depinde de parametrii n si p si este de obicei
notata prin Bi(n,p). Aceasta variabila
aleatoare X urmeaza legea binomiala de parametrii nsi p
daca are distributia:
X: 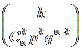 ,
, 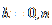 ,
p+q=1
,
p+q=1
adica
Pr( X = k ) =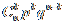 unde X este evenimentul
de interes.
unde X este evenimentul
de interes.
Problema 1: Aruncam o moneda de n=7 ori. Consideram
succes daca am aruncat "cap". Deoarece aruncam cu o moneda
nemasluita sansa de succes este de 50%, deci avem p=0,5.
X: 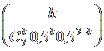
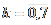
adica
Pr( X = k ) =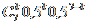
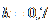
Calculati probabilitatile pentru
aceasta distributie.
Instructiuni:
 Introduceti in
Excel urmatorul tabel:
Introduceti in
Excel urmatorul tabel:
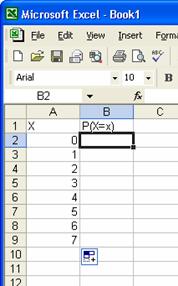
 In celula B2 vom
calcula probabilitatea a 0 succese P(X=0).
In celula B2 vom
calcula probabilitatea a 0 succese P(X=0).
Din meniul
Insert Function selectam functia BINOMDIST.
Click OK. Complectati fereastra de dialog ca
in figura de mai jos:
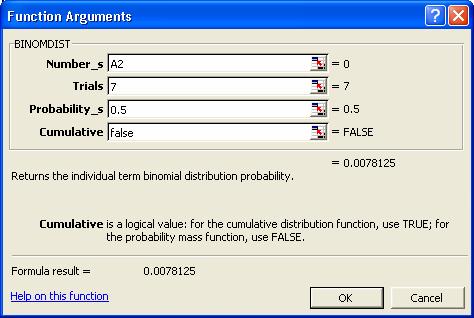
Number_s: Numarul de succese, in cazul nostru 0 cu
referinta A2.
Trials: Numarul total de incercari, in cazul nostru
de aruncari, 7.
Probability_s: probabilitatea succesului, in cazul nostru la aruncare
sa iasa "cap". Probabilitatea este 0,5.
Cumulative: True daca dorim probabilitati cumulate,
False daca dorim probabilitati necumulate. In cazul nostru am introdus False.
 Dupa ce executam click pe butonul OK in celula B2 vom avea
valoarea Aceasta este probabilitatea ca
aruncand moneda de 7 ori sa nu avem nici un succes.
Dupa ce executam click pe butonul OK in celula B2 vom avea
valoarea Aceasta este probabilitatea ca
aruncand moneda de 7 ori sa nu avem nici un succes.
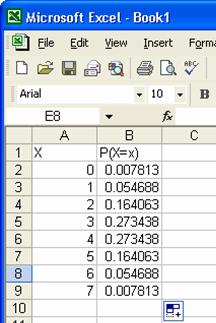
 Restul de probabilitati se calculeaza prin copierea formulei
in celelalte celule din coloana B prin selectarea domeniului B2:B8 si
alegerea optiunii Fill Down din meniul Edit.
Restul de probabilitati se calculeaza prin copierea formulei
in celelalte celule din coloana B prin selectarea domeniului B2:B8 si
alegerea optiunii Fill Down din meniul Edit.
Problema
2: Calculati
probabilitatile binomiale cumulative pentru exemplul de mai sus.
Instructiuni
 In foaia de lucru
Excel, in celula C1 introduceti urmatorul text P(x<=X).
In foaia de lucru
Excel, in celula C1 introduceti urmatorul text P(x<=X).
 In celula C2
calculati probabilitatea binomiala ca numarul de esecuri sa fie mai mic sau egal cu 0 astfel: dupa
selectarea celulei C2 alegeti din meniul Insert Function functia
BINOMDIST. Completati fereastra de dialog care apare ca mai jos:
In celula C2
calculati probabilitatea binomiala ca numarul de esecuri sa fie mai mic sau egal cu 0 astfel: dupa
selectarea celulei C2 alegeti din meniul Insert Function functia
BINOMDIST. Completati fereastra de dialog care apare ca mai jos:
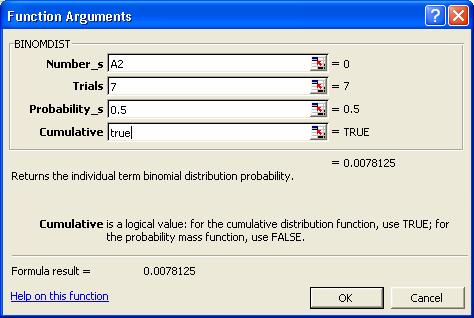
 Modul de completare este acelasi ca la Problema 1 cu deosebirea
ca in campul Cumulative vom introduce True. Vom obtine 007813 care este probabilitatea
cumulata ca sa avem la 7 aruncari cu zarul mai putin sau
egal cu 0 succese, adica 0 succese.
Modul de completare este acelasi ca la Problema 1 cu deosebirea
ca in campul Cumulative vom introduce True. Vom obtine 007813 care este probabilitatea
cumulata ca sa avem la 7 aruncari cu zarul mai putin sau
egal cu 0 succese, adica 0 succese.
 Pentru a calcula si celelalte probabilitati cumulative
selectati domeniul de celule C2:C7 si copiati formula cu
ajutorul comenzii Fill Down din meniul Edit.
Pentru a calcula si celelalte probabilitati cumulative
selectati domeniul de celule C2:C7 si copiati formula cu
ajutorul comenzii Fill Down din meniul Edit.
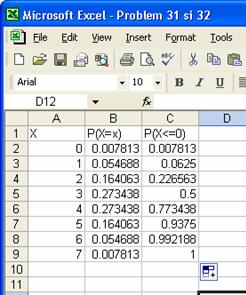
Probabilitatea de a cadea "cap" de 2 ori din 7
aruncari ale unei monede este 0.164063, de a cadea cap de 3 ori din 7
este 0.273438 etc. Sansa cea mai mare este de a avea 3 sau 4 aruncari
la care sa avem "cap" din 7.
Probabilitatile
calculate in coloana C sunt probabilitatile ca din 7 aruncari sa avem cel mult x succese. De exemplu pentru x=3 avem
calculata probabilitatea 0,226563 ca din 7 aruncari sa avem cel
mult 3 succese, adica sa avem 0 sau 3
succese. Probabilitatea ca sa avem una dintre variantele 0 , . ,7 succese din 7 aruncari este 1 deoarece nu
exista alta posibilitate, in mod sigur una dintre aceste variante va
avea loc.
Distributia Poisson
Variabila
aleatoare Poisson este o variabila discreta care ia o infinitate
numarabila de valori 0,1,2,3, . .. care reprezinta numarul de realizari a unui
eveniment intr-un timp dat.
Aceasta
variabila aleatoare X care urmeaza legea de distributie Poisson P() are urmatoarea distributie:
X: 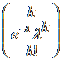 ,
k =0,1,2,3, . .
,
k =0,1,2,3, . .
unde este
un parametru care caracterizeaza legea, care reprezinta numarul
mediu asteptat de realizari ale evenimentului in intervalul
considerat si deci
Pr( X = k ) = 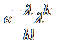 , k=0,1,2,3, . .
, k=0,1,2,3, . .
Problema
3. Rata anuala de
incidenta a varicelei printre copiii este de 0.01, adica un
copil dintr-o suta este diagnosticat cu varicela. La
o gradinita cu 300 de copii dintr-o localitate A au fost
diagnosticati 5 copii cu varicela. Care este probabilitatea a 5
astfel de cazuri stiind ca rata imbolnavirii este de 0,01? Ar trebui gradinita sa
ia masuri urgente?
Instructiuni:
 Introduceti in
Excel urmatorul tabel:
Introduceti in
Excel urmatorul tabel:
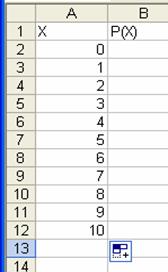
 In celula B2 vom
calcula probabilitatea sa avem 0 imbolnaviri
P(X=0).
In celula B2 vom
calcula probabilitatea sa avem 0 imbolnaviri
P(X=0).
Din meniul
Insert Function selectam functia POISSON.
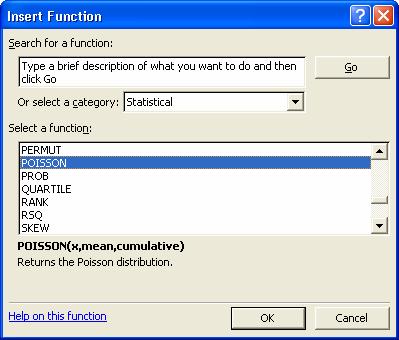
Click OK. Complectati fereastra de dialog ca
in figura de mai jos:
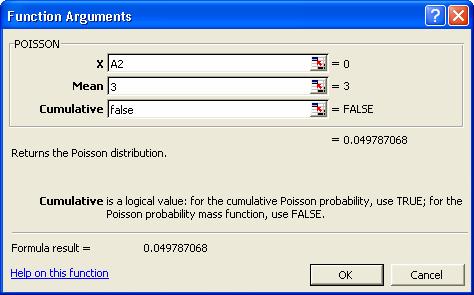
X: Numarul de imbolnaviri, in cazul nostru 0 cu
referinta A2.
Mean: Este numarul asteptat stiind rata de
imbolnavire 0.01. Pentru a calcula numarul asteptat vom
inmulti numarul de copii din gradinita 300 cu rata
imbolnavirii 0.01 si vom obtine 3.
Cumulative: True daca dorim probabilitati cumulate,
False daca dorim probabilitati necumulate. In cazul nostru am introdus False.
 Dupa ce executam click pe butonul OK in celula B2 vom
avea valoarea Aceasta este probabilitatea ca
sa avem 0 imbolnaviri.
Dupa ce executam click pe butonul OK in celula B2 vom
avea valoarea Aceasta este probabilitatea ca
sa avem 0 imbolnaviri.
 Restul de
probabilitati se calculeaza prin copierea formulei in celelalte
celule din coloana B prin selectarea domeniului B2:B8 si alegerea
optiunii Fill Down din meniul Edit.
Restul de
probabilitati se calculeaza prin copierea formulei in celelalte
celule din coloana B prin selectarea domeniului B2:B8 si alegerea
optiunii Fill Down din meniul Edit.
Problema
4: Calculati
probabilitatile binomiale cumulative pentru exemplul de mai sus.
Instructiuni
 In foaia de lucru
Excel, in celula C1 introduceti urmatorul text P(x<=X).
In foaia de lucru
Excel, in celula C1 introduceti urmatorul text P(x<=X).
 In celula C2
calculati probabilitatea ca numarul de inbolnaviri sa fie mai mic sau egal cu 0 astfel: dupa
selectarea celulei C2 alegeti din meniul Insert Function
functia POISSON. Completati fereastra de dialog care apare ca
mai jos:
In celula C2
calculati probabilitatea ca numarul de inbolnaviri sa fie mai mic sau egal cu 0 astfel: dupa
selectarea celulei C2 alegeti din meniul Insert Function
functia POISSON. Completati fereastra de dialog care apare ca
mai jos:
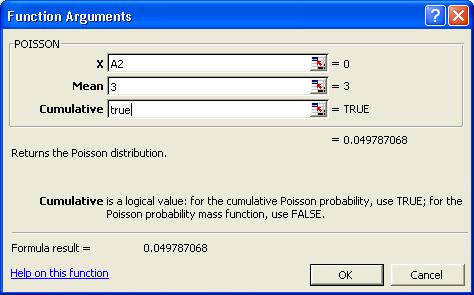
 Modul de completare este acelasi ca la Problema 3 cu deosebirea
ca in campul Cumulative vom introduce True. Vom obtine care este probabilitatea
cumulata ca sa avem cel 0 imbolnaviri, adica nici o imbolnavire.
Modul de completare este acelasi ca la Problema 3 cu deosebirea
ca in campul Cumulative vom introduce True. Vom obtine care este probabilitatea
cumulata ca sa avem cel 0 imbolnaviri, adica nici o imbolnavire.
 Pentru a calcula si celelalte probabilitati cumulative
selectati domeniul de celule C2:C7 si copiati formula cu
ajutorul comenzii Fill Down din meniul Edit.
Pentru a calcula si celelalte probabilitati cumulative
selectati domeniul de celule C2:C7 si copiati formula cu
ajutorul comenzii Fill Down din meniul Edit.
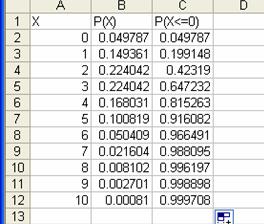
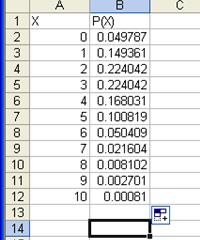
Probabilitatea de avea 0 imbolnaviri este 0.49787,
de a avea o imbolnavire 0,149361, iar cea mai mare probabilitate este de a
avea 2 sau 3 imbolnaviri 0,224042. probabilitatea
cea mai mica este la 10 imbolnaviri 0.00081. Gradinita ar
trebui sa ia masuri daca sunt raportate 10 cazuri de
varicela.
Probabilitatile calculate in coloana C sunt
probabilitatile ca din 300 de copii sa se
imbolnaveasca cel mult x copii. De exemplu pentru x=3
imbolnaviri avem calculata probabilitatea 0,647232 ca din 300 de
copii sa avem cel mult 3 imbolnaviri, adica sa avem 0,1,2 sau 3 cazuri de varicela. Probabilitatea ca
sa avem una dintre variantele 0,1, . ,10 imbolnaviri este 0,99 aproape
1.
Distributia
Hipergeometrica
Distributia hipergeometrica este analoaga
cu distribuia binomiala doar ca nu avem independenta
asigurata, adica rezultatul unei incercari depinde de rezultatul
incercarilor de dinaintea ei.
Variabila
aleatoare X urmeaza legea hipergeometrica daca are
distributia:
X: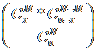
unde: M este numarul de succese in
populatie, x numarul de succese din incercari, N talia
populatiei, n numarul incercarilor.
Problema
5: Trebuie testat un nou
tratament. S-au oferit 25 de voluntari 15 femei, 10 barbati. Dintre ei vor fi alesi doar 7
persoane in mod aleator. Care este probabilitatea ca
dintre ei 3 sa fie barbati si 4 sa fie femei?
Probabilitatea de a selecta o femeie este 15/25=0,6.
Daca selectam o femeie, probabilitatea ca si a doua
selectie sa fie tot o femeie este de 14/24=0,583, deoarece nu dorim
sa selectam o femeie de doua ori. In cazul nostru selectarea unei femei inseamna succes M=15, x=0,1,2,3,4, N=25, n=7.
Instructiuni:
 Introduceti in
Excel urmatorul tabel:
Introduceti in
Excel urmatorul tabel:
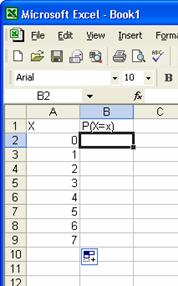
X este evenimentul de a selecta o femeie. Se fac 7
selectii si exista 8 posibilitati: de a selecta
0,1, . ,7 femei. Fiecare posibilitate are o
probabilitate pe care o vom calcula in coloana B.
 In celula B2 vom
calcula probabilitatea a 0 succese P(X=0).
In celula B2 vom
calcula probabilitatea a 0 succese P(X=0).
Din meniul
Insert Function selectam functia HYPGEOMDIST
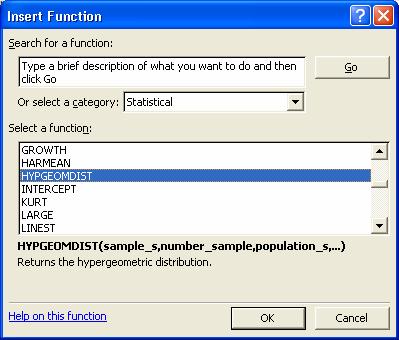
Click OK. Complectati fereastra de dialog ca
in figura de mai jos:
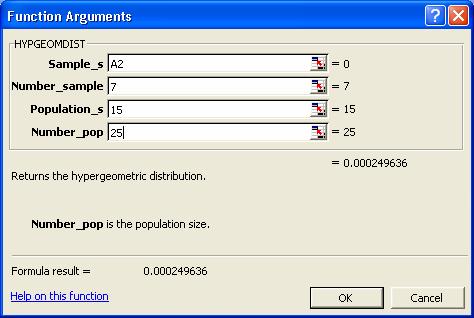
Sample_s: Numarul de succese pentru prima posibilitate P(X=0)
este 0. Vom introduce referinta A2.
Number_sample:
Numarul de posibilitati -
selectia pe care o facem are 7 persoane.
Population_s: Numarul total de succese in populatie, in cazul
nostru numarul total de femei 15.
Number_pop:
Numarul total al populatiei din
care se face selectia, in cazul nostru avem 25 voluntari.
 Dupa ce executam click pe butonul OK in celula B2 vom avea
valoarea Aceasta este probabilitatea
facand 7 selectii aleatoare sa nu selectam nici o femeie.
Dupa ce executam click pe butonul OK in celula B2 vom avea
valoarea Aceasta este probabilitatea
facand 7 selectii aleatoare sa nu selectam nici o femeie.
 Restul de
probabilitati se calculeaza prin copierea formulei in celelalte
celule din coloana B prin selectarea domeniului B2:B8 si alegerea
optiunii Fill Down din meniul Edit.
Restul de
probabilitati se calculeaza prin copierea formulei in celelalte
celule din coloana B prin selectarea domeniului B2:B8 si alegerea
optiunii Fill Down din meniul Edit.
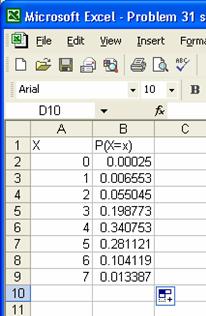
Cel mai
probabil este sa selectam 4 femei si
trei barbati: 0.340753 si acesta este si raspunsul
problemei.
Distributii
de probabilitate continue
Variabila continua este acea variabila care ia
ca valori numere reale situate intr-un interval. Vom descrie cateva
distributii de probabilitate continue: distributia normala,
distributia t, distributia F si distributia hi-patrat.
Un test statistic este utilizat pentru verificarea unei
ipoteze statistice, numita ipoteza nula, in care nu exista nici
o schimbare, variabilele comparate nu difera. Scopul unui test este de
arata ca o astfel de ipoteza nu este adevarata. Se
calculeaza un parametru statistic care este o variabila aleatoare de
selectie, care urmeaza o anumita lege de probabilitate. Se
stabileste regiunea critica pentru care ipoteza nula nu este
adevarata. Daca
parametrul calculat apartine regiunii critice atunci vom respinge ipoteza nula. Alegerea regiunii critice se
face in functie de marimea riscului de eroare in respingerea ipotezei
nule pe care suntem dispusi sa-l acceptam si acesta este
nivelul de semnificatie . De obicei se alege un nivel de
semnificatie de 5%, caz in care se calculeaza si p. Valoarea lui
p este calculata de orice program statistic. P este probabilitatea de
semnificatie a testului statistic, nivelul de semnificatie (eroarea)
cel mai mic la care ipoteza nula poate fi respinsa.
Distributia normala
Variabila
aleatoare X urmeaza legea normala de
parametrii m si <0 daca are densitatea de probabilitate
urmatoare:
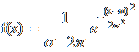
Graficul acestei functiei are o forma de clopot
si se numeste clopotul lui Gauss.
Pentru distributia normala Excel ofera
cateva functii:
NORMDIST - calculeaza distributia normala
cumulativa pentru variabila X, media si deviatia standard date,
NORMINV - calculeaza inversa distributiei normale
cumulative pentru o probabilitate specificata, o medie si o
deviatie standard specificata,
NORMSDIST - calculeaza distributia normala
cumulativa standard pentru o valoare specificata,
NORMSINV - returneaza inversa distributiei normale
cumulative standard pentru o valoare specificata,
STANDARDIZE - calculeaza un scor standard pentru o valoare X, o
medie si o deviatie standard specificate.
Problema
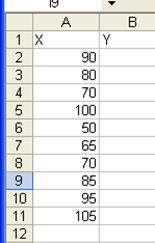
6. Se dau valorile variabilei
Tensiune arteriala diastolica pentru 10 pacienti. Calculati
media aritmetica si deviatia standard. Transformati fiecare
valoare a variabilei Tensiune arteriala diastolica intr-o valoare
standardizata Z cu ajutorul functiei STANDARDIZE (Variabila
standardizata Z urmeaza legea normala N(0,1), unde media este 0
si deviatia standard este 1).
Instructiuni
Pentru calcularea mediei aritmetice. Selectam celula D1 si din meniul Insert
alegem optiunea Function, selectam functia Average:
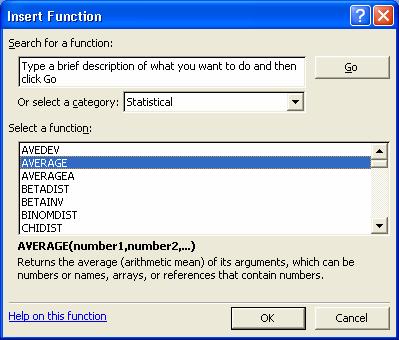
Click OK.
Completam fereastra de dialog ca in figura de mai jos, iar dupa
apasarea butonului OK vom afla valoarea mediei:81.
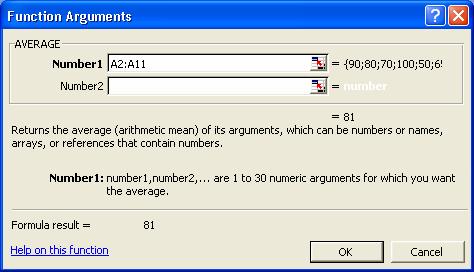
Pentru
calcularea deviatiei standard: Selectam celula D2 si din meniul Insert
alegem optiunea Function, selectam functia STDEV:
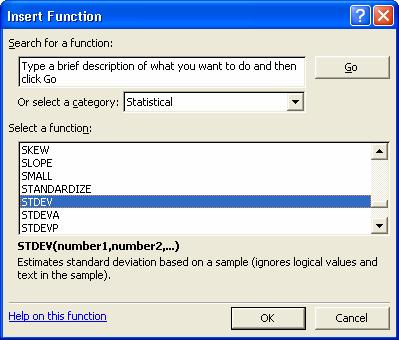
Click OK.
Completam fereastra de dialog ca in figura de mai jos, iar dupa
apasarea butonului OK vom afla valoarea deviatiei standard: 17,2884.
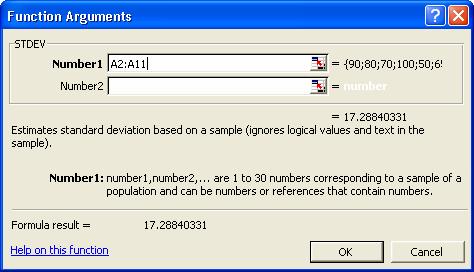
Vom avea tabelul:
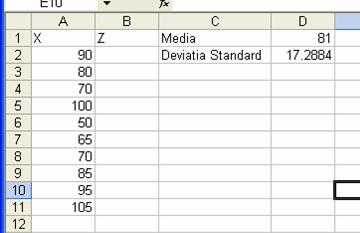
Vom
calcula valorile standardizate: selectati celula B2 si din meniul Insert
alegem optiunea Function, selectam functia STANDARDIZE.
Click OK.
Complectati fereastra de dialog ca in figura de mai
jos:
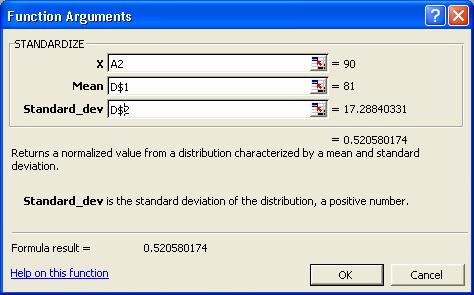
X: vom introduce referinta celulei in care se
gaseste prima valoare a variabilei A2.
Mean: vom introduce referinta absoluta sau fixa
la medie: D$1.
Deviatia
standard: vom introduce referinta
absoluta la deviatia standard: D$2.
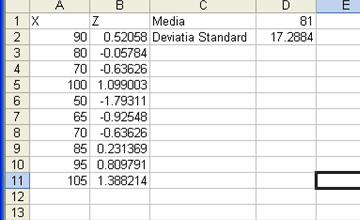
 Dupa ce executam click pe butonul OK in celula B2 vom
avea valoarea Aceasta este valoarea
standardizata.
Dupa ce executam click pe butonul OK in celula B2 vom
avea valoarea Aceasta este valoarea
standardizata.
 Restul de valori se
calculeaza prin copierea formulei in celelalte celule din coloana B prin
selectarea domeniului B2:B11 si alegerea optiunii Fill Down
din meniul Edit.
Restul de valori se
calculeaza prin copierea formulei in celelalte celule din coloana B prin
selectarea domeniului B2:B11 si alegerea optiunii Fill Down
din meniul Edit.
Dupa
calcularea valorilor vom sorta descendent variabila X. Selectam domeniul
A1:B11.
!!! La
sortare nu este necesara selectia tabelului, ci doar a unei singure
celule din tabel, iar Excelul in momentul alegerii optiunii SORT selecteaza intregul tabel. In cazul
nostru se considera si media si deviatia standard ca
facand parte din tabel. Din aceasta cauza este
necesara selectarea celor doua coloane in prealabil.
Din meniul
Data alegem optiunea Sort. Alegem ca prima cheie de sortare
variabila X din lista derulanta. Alegem prin click pe butonul Descending
modul de sortare descendent.
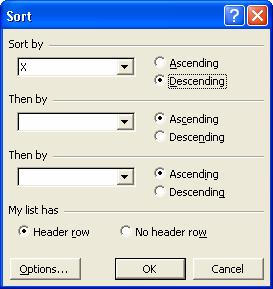
Click OK. Vom avea astfel urmatorul rezultat:
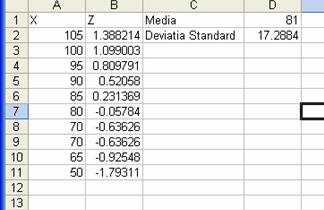
Avantajul
de a lucra cu valori standardizate este ca
daca lucram ca variabile continue cu o distributie normala
putem determina probabilitatea ca sa obtinem o valoare mai mare sau
mai mica decat una specificata. Vom calcula
aceasta probabilitate cu functia NORMSDIST.
Aceasta functie intoarce aceleasi valori ca un
tabel de distributie normala, doar ca se pot afla
probabilitatile normale si pentru valori cu trei sau mai multe
zecimale pentru care nu exista valori in tabele.
Problema 7 Introduceti in Excel urmatorul tabel:
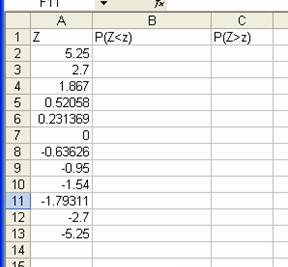
Calculati probabilitatile normale N(0,1) de distributie p pentru valorile de mai sus. (media este 0 si deviatia standard este 1)
Instructiuni
Introduceti in Excel tabelul de mai sus.
Pentru
calculul probabilitatii selectati celula B2 ,
introduceti functia NORMSDIST din meniul Insert optiunea
Function.
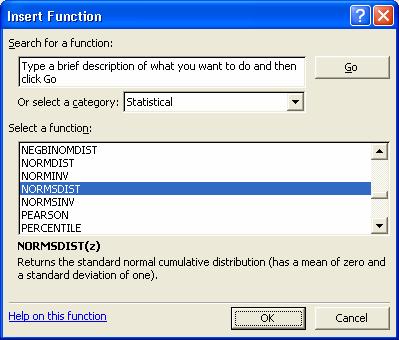
Complectati fereastra de dialog ca in figura de mai
jos:
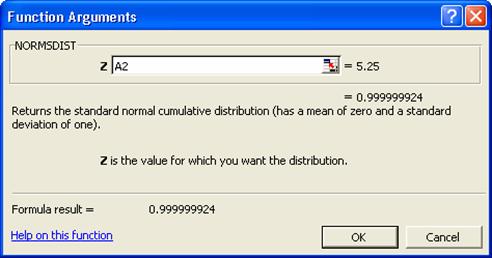
Z: vom
introduce referinta celulei in care se gaseste prima valoare a
variabilei Z: A2.
 Dupa ce executam click pe butonul OK in celula B2 vom
avea valoarea Aceasta este valoarea
probabilitatii ca z sa fie mai mic de 5.25.
Dupa ce executam click pe butonul OK in celula B2 vom
avea valoarea Aceasta este valoarea
probabilitatii ca z sa fie mai mic de 5.25.
 Restul de valori se calculeaza prin copierea formulei in celelalte
celule din coloana B prin selectarea domeniului B2:B11 si alegerea
optiunii Fill Down din meniul Edit.
Restul de valori se calculeaza prin copierea formulei in celelalte
celule din coloana B prin selectarea domeniului B2:B11 si alegerea
optiunii Fill Down din meniul Edit.
 Obtinem
urmatorul tabel:
Obtinem
urmatorul tabel:
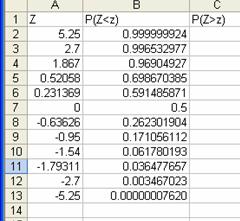
Normsinv
Uneori se doreste gasirea valorilor Z care
definesc un anumit punct in distributie, cum ar fi mai mic de 10% sau mai
mare ca 5%. Putem folosi NORMSINV.
Lower 1% - ce valoare a lui Z descrie mai mic de 1% a
distributiei normale?
Distributia
t
Problema
8. Se dau diverse valori ale
parametrului testului t care urmeaza legea de distributie t si
care a fost calculat dupa urmatoarea formula:
t = 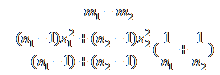 ,
,
urmeaza o lege
Student cu (n1 + n2 -2) grade de libertate, unde n1
si n2 sunt talia, m1, m2 sunt mediile celor doua variabile comparate,
s1 si s2 sunt variatiile. Sa se calculeze
p_value pentru urmatoarele t-uri.
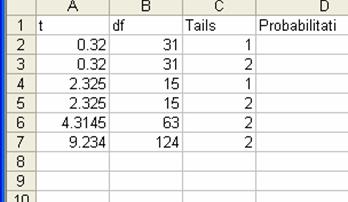
Instructiuni
Introduceti in Excel tabelul de mai sus.
Pentru
calculul probabilitatii selectati celula D2 ,
introduceti functia TDIST din meniul Insert
optiunea Function.
Complectati fereastra de dialog ca in figura de mai
jos:
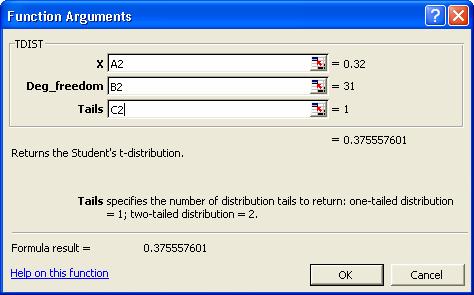
X: vom introduce referinta celulei in care se
gaseste prima valoare a parametrului t: A2.
Deg_freedom:
gradele de libertate, vom introduce
referinta B2.
Tails: daca testul este unilateral
se introduce 1, daca este bilateral se introduce 2 vom introduce
referinta C2.
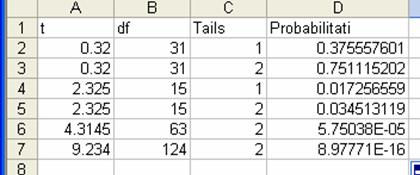
 Dupa ce executam click pe butonul OK in celula D2 vom avea
valoarea Aceasta este valoarea probabilitatii pentru t 0,32, 31 de grade
de libertate si pentru test unilateral.
Dupa ce executam click pe butonul OK in celula D2 vom avea
valoarea Aceasta este valoarea probabilitatii pentru t 0,32, 31 de grade
de libertate si pentru test unilateral.
 Restul de valori se calculeaza prin copierea formulei in celelalte
celule din coloana D prin selectarea domeniului D2:D7 si alegerea
optiunii Fill Down din meniul Edit.
Restul de valori se calculeaza prin copierea formulei in celelalte
celule din coloana D prin selectarea domeniului D2:D7 si alegerea
optiunii Fill Down din meniul Edit.
 Obtinem
urmatorul tabel:
Obtinem
urmatorul tabel:
Problema
9. Calculati valoarea
parametrilor t care urmeaza legea de distributie t stiind
valorile p si gradele de libertate:
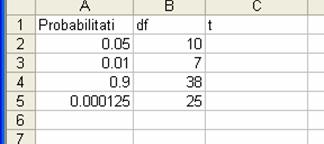
Instructiuni
Introduceti in Excel tabelul de mai sus.
Pentru
calculul valorii critice t selectati celula C2 ,
introduceti functia TINV din meniul Insert optiunea
Function.
Complectati fereastra de dialog ca in figura de mai
jos:

Probability: vom introduce referinta celulei in care se
gaseste prima probabilitate: A2.
Deg_freedom: gradele de libertate, vom introduce referinta B2.
 Dupa ce executam click pe butonul OK in celula D2 vom avea
valoarea 2.228139238 Aceasta este valoarea lui t pentru p 0,05, 10 de grade de libertate.
Dupa ce executam click pe butonul OK in celula D2 vom avea
valoarea 2.228139238 Aceasta este valoarea lui t pentru p 0,05, 10 de grade de libertate.
 Restul de valori se calculeaza prin copierea formulei in celelalte
celule din coloana C prin selectarea domeniului C2:C5 si alegerea
optiunii Fill Down din meniul Edit.
Restul de valori se calculeaza prin copierea formulei in celelalte
celule din coloana C prin selectarea domeniului C2:C5 si alegerea
optiunii Fill Down din meniul Edit.
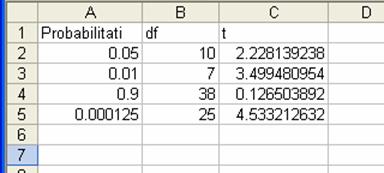
 Obtinem
urmatorul tabel:
Obtinem
urmatorul tabel:
Distributia
F
Problema
10. Se dau diverse valori ale
parametrului testului F care urmeaza legea de distributie F si
care a fost calculat dupa urmatoarea formula:
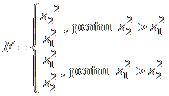 .
.
urmeaza o lege
F, s1 si s2 sunt variatiile celor doua variabile comparate. Sa se calculeze p_value pentru urmatoarele F-uri.
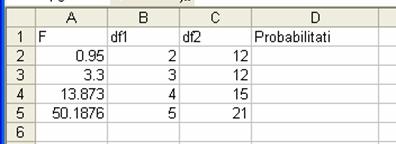
Instructiuni
Introduceti in Excel tabelul de mai sus.
Pentru
calculul probabilitatii selectati celula D2 ,
introduceti functia FDIST din meniul Insert optiunea
Function.
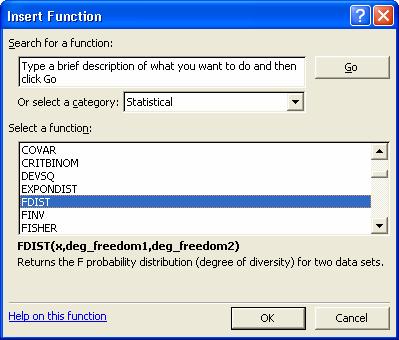
Complectati fereastra de dialog ca in figura de mai
jos:
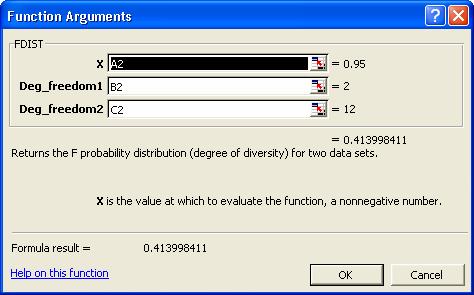
X: vom introduce referinta celulei in care se gaseste
prima valoare a parametrului t: A2.
Deg_freedom1:
gradele de libertate - numerator degrees
of freedom, vom introduce referinta B2.
Deg_freedom2:
denominator grade de libertate. Vom
introduce referinta C2.
 Dupa ce executam click pe butonul OK in celula D2 vom
avea valoarea Aceasta este valoarea probabilitatii pentru F 0,95.
Dupa ce executam click pe butonul OK in celula D2 vom
avea valoarea Aceasta este valoarea probabilitatii pentru F 0,95.
 Restul de valori se
calculeaza prin copierea formulei in celelalte celule din coloana D prin
selectarea domeniului D2:D5 si alegerea optiunii Fill Down din
meniul Edit.
Restul de valori se
calculeaza prin copierea formulei in celelalte celule din coloana D prin
selectarea domeniului D2:D5 si alegerea optiunii Fill Down din
meniul Edit.
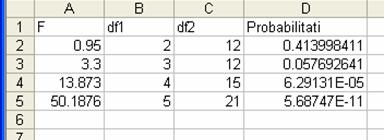
 Obtinem
urmatorul tabel:
Obtinem
urmatorul tabel:
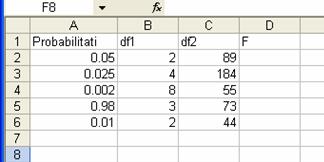
Problema 11.
Calculati valoarea parametrilor F care urmeaza legea de
distributie F stiind valorile p si gradele de libertate:
Instructiuni
Introduceti in Excel tabelul de mai sus.
Pentru
calculul valorii critice F selectati celula D2 ,
introduceti functia FINV din meniul Insert
optiunea Function.
Complectati fereastra de dialog ca in figura de mai
jos:
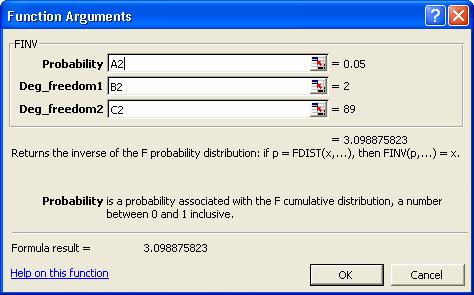
Probability: vom introduce referinta celulei in care se
gaseste prima probabilitate: A2.
Deg_freedom1:
gradele de libertate - numerator degrees
of freedom, vom introduce referinta B2.
Deg_freedom2:
denominator grade de libertate. Vom
introduce referinta C2.
 Dupa ce executam click
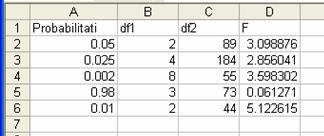
pe butonul OK in celula D2 vom avea valoarea 3.098875823 Aceasta
este valoarea lui F pentru p 0,05.
Dupa ce executam click
pe butonul OK in celula D2 vom avea valoarea 3.098875823 Aceasta
este valoarea lui F pentru p 0,05.
 Restul de valori se calculeaza prin copierea formulei
in celelalte celule din coloana D prin selectarea domeniului D2:D6 si
alegerea optiunii Fill Down din meniul Edit.
Restul de valori se calculeaza prin copierea formulei
in celelalte celule din coloana D prin selectarea domeniului D2:D6 si
alegerea optiunii Fill Down din meniul Edit.
 Obtinem urmatorul tabel:
Obtinem urmatorul tabel:
Distributia Hi-patrat
In mod
asemanator puteti rezolva urmatoarele probleme:
Problema
12. Se dau diverse valori ale
parametrului testului Hi-patrat care urmeaza legea de
distributie Hi-patrat. Sa
se calculeze p_value
|
Parametru
|
df
|
Probabilitate
|
|
|
|
|
|
|
|
|
|
|
|
|
Instructiuni Se utilizeaza functia CHIDIST.
Problema
13. Calculati valoarea
parametrilor Hi-patrat care urmeaza legea de distributie
Hi-patrat stiind valorile p si gradele de libertate:
Instructiuni Se utilizeaza functia CHIINV.
Alte functii asemanatoare: BETADIST,
BETAINV -pentru distributia beta de densitate de probabilitate, GAMMADIST,
GAMMAINV - pentru distributia gamma, EXPONDIST - pentru
distributia exponentiala, FISHER, FISHERINV - pentru
distributia Fisher, WEIBULL - pentru distributia Weibull etc.








 ,
k =0,1,2,3, . .
,
k =0,1,2,3, . .
























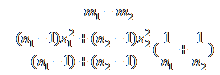 ,
,







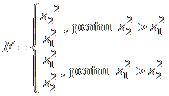 .
.






