Inele factoriale
Definitia 1. Un inel integru A se
numeste inel factorial sau cu descompunere unica in factori primi
(ireductibili), daca orice element neinversabil si nenul din A se
descompune intr-un produs finit de elemente prime.
Din
teorema 3.7 rezulta ca orice inel principal este factorial. In
particular, inele Z, Z[i],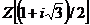 si orice inel de polinoame de o nedeterminata
cu coeficienti intr-un corp este inel factorial.
si orice inel de polinoame de o nedeterminata
cu coeficienti intr-un corp este inel factorial.
Lema
2. Daca A este inel factorial , descompunerea unui element in produs
de elemente prime este unica in afara de ordinea factorilor si o
asociere a lor. Adica, daca
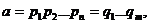
unde 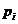 si
si
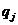 , i=1, . ,n, j=1, . .m sunt elemente prime, atunci n=m li,
schimband eventual eventual ordinea factorilor, avem
, i=1, . ,n, j=1, . .m sunt elemente prime, atunci n=m li,
schimband eventual eventual ordinea factorilor, avem 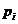 =
=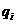
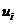 , unde
, unde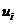 sunt elemente inversabile, i=1, . ,n.
sunt elemente inversabile, i=1, . ,n.
Demonstratie.
Vom face o inductie dupa numarul minim al factorilor din cele
doua descompuneri. Vom presupune, de exemplu, ca n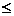 m. Atunci, pentru n=1 avem
m. Atunci, pentru n=1 avem 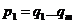 si deoarece
si deoarece 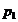 este ireductibil
rezulta ca
este ireductibil
rezulta ca 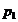 este asociat cu
unul dintre
este asociat cu
unul dintre 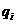 ,1
,1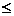 j
j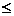 m.Putem presupune ca acela este
m.Putem presupune ca acela este 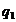 . Atunci produsul
. Atunci produsul 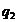 . ~1 si deci toti
. ~1 si deci toti 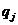 ,2
,2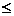 j
j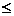 m, ar fi elemente inversabile ale linelului A, ceea ce
nu este posibil. Deci m=1 si afirmatia este dovedita in acest
caz . Presupuneam afirmatia devedita pentru orice doua descompuneri
in care una are mai putin de n factori.
m, ar fi elemente inversabile ale linelului A, ceea ce
nu este posibil. Deci m=1 si afirmatia este dovedita in acest
caz . Presupuneam afirmatia devedita pentru orice doua descompuneri
in care una are mai putin de n factori.
Atunci
, in descompunerea (a) de mai sus, din faptul ca 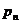 este element
prin rezulta ca
este element
prin rezulta ca 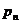 divide cel
putin unul dintre
divide cel
putin unul dintre 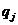 ,1
,1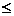 j
j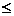 m.Putem presupune ca
m.Putem presupune ca 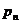 |
|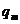 si deoarece
si deoarece 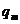 este
ireductibil, rezulta ca
este
ireductibil, rezulta ca 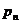 ~
~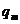 . Deci
. Deci 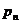 =
=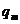 u, unde u este element inversabil in A. Deci din (1)
obtinem, simplificand cu
u, unde u este element inversabil in A. Deci din (1)
obtinem, simplificand cu 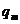 ,
,
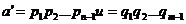
Deoarece 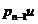 este element prim , rezulta ca avem
aici doua descompuneri ale elementului a' in produs de elemente prime
si, din ipoteza inductiva, rezulta n-1=m-1, deci n=m, iar
dupa o eventual renumerotare
este element prim , rezulta ca avem
aici doua descompuneri ale elementului a' in produs de elemente prime
si, din ipoteza inductiva, rezulta n-1=m-1, deci n=m, iar
dupa o eventual renumerotare 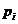 ~
~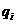 ,1
,1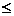 i
i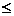 n-1 si cu aceasta totul este demonstrat.
n-1 si cu aceasta totul este demonstrat.
Daca
A este un inel factorial , atunci luand din fiecare clasa de elemente asociate
prime cate un reprezentant, obtinem o multime 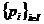 de elemente prime, astfel incat orice element a din A,
a
de elemente prime, astfel incat orice element a din A,
a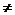 0 se scrie sub forma:
0 se scrie sub forma:
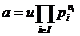
Cu 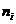 , i
, i 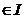 ,numere intregi nenegative si numai un numar
finit sunt nenule, iar u un element inversabil in A. Unicitatea descompunerii
se exprima atunci prin faptul ca daca
,numere intregi nenegative si numai un numar
finit sunt nenule, iar u un element inversabil in A. Unicitatea descompunerii
se exprima atunci prin faptul ca daca
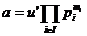
Este o alta
scriere a lui a sub forma
, atunci u=u' si 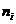 =
=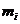 , i
, i 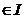 .
.
Teorema 3. Fie A un inel integru. Urmatoarele afirmatii sunt echivalente:
a)
A este inel factorial.
b)
Orice element nenul si
neinversabil din A se descompune in produs finit de elemente ireductibile
si orice element ireductibil este prim.
c)
Orice element nenul si
neinversabil din A se descompune in produs finit de elemente ireductibile
si doua astfel de descompuneri sunt unice in afara de ordinea
factorilor si de asociere.
d)
Orice element nenul si
neinversabil din A se descompune in produs finit de elemente ireductibile
si orice doua elemente din A au un cel mai mare divizor comun.
Demonstratie. Fie a un element
ireductibil din inelul A. Atunci din faptul ca el este produs de elemente
prime rezulta ca se divide cu un element prim p. Dar p fiind
neinversabil, este asciat cu a.
Revenind la demonstratia
teoremei, se observa ca din a) si b) rezulta c). Pentru a
arata ca c)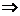 b) este suficient sa observam ca din c)
rezulta ca orice element ireductibil din A este prim. Fie q un
element ireductibil si sa presupunem ca q|ab. Atunci:
b) este suficient sa observam ca din c)
rezulta ca orice element ireductibil din A este prim. Fie q un
element ireductibil si sa presupunem ca q|ab. Atunci:
ab=qq'.
Considerand descompuneri ale lui a
,b si q' in factori ireductibili si utilizand unicitatea
descompunerii in factori ireductibili din relatia (3), rezulta q|ab.
Pana
acum am aratat ca a),b) si c) sunt echivalente. Din
propozitia 1.15 rezulta ca d)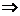 b). Este suficient sa observam
urmatoarea lema.
b). Este suficient sa observam
urmatoarea lema.
Lema
5. Intr-un inel factorial orice doua elemente au cel mai mare divizor
comun.
Demonstratie. Fie a si b
doua elemente din inel factorial A. In cazul in care unul dintre ele este
nul , afirmatia este evidenta. Putem deci presupune ca a si
b sunt nenule si fie , i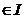 , un sistem de
reprezentanti de elemente prime . Atunci fie
, un sistem de
reprezentanti de elemente prime . Atunci fie
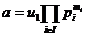
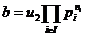
Descompunerile lui a
si b in produs de elemente prime si
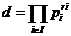
unde r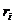 =min(
=min(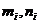 ),i
),i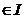 . Atunci este clar ca d este divizor comun al lui
a si b si daca d' este divizor comun al elementelor a si b,
. Atunci este clar ca d este divizor comun al lui
a si b si daca d' este divizor comun al elementelor a si b,
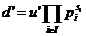
atunci din faptul
ca d' divide pe a rezulta 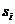
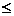
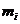 , i
, i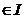 , iar din faptul ca d' divide pe b rezulta
, iar din faptul ca d' divide pe b rezulta 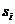
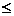 n, i
n, i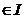 . Deci
. Deci 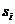
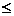
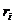 i
i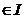 , de unde obtinem ca d' divide pe d.
Asadar, d este cel mai mare divizor comun al elementelor a si b
si lema este demonstrata.
, de unde obtinem ca d' divide pe d.
Asadar, d este cel mai mare divizor comun al elementelor a si b
si lema este demonstrata.
Din lema de mai sus rezulta
ca intr-un inel factorial exista si cel mai mic multiplu a
doua elemente daca se tine seama de propozitia 1.9. Se
poate insa vedea imediat, cu notatiile din lema precedenta,
ca elementul
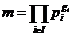
Unde 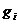 = max(
= max(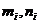 ) este cel mai mic multiplu comun al elementelor a
si b.
) este cel mai mic multiplu comun al elementelor a
si b.
Propozitia
6. Fie A un inel factorial si a, 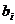
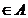 , i=1,,s. Daca (a,
, i=1,,s. Daca (a, 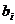 )=1, pentru i=1,,s, atunci
)=1, pentru i=1,,s, atunci 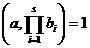
Demonstratie. Va fi suficient
sa aratam ca nu exista niciun element prim in A care
sa divida pe a si pe 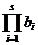 .
Fie p un astfel de element prim. Atunci rezulta ca exista un j,
1
.
Fie p un astfel de element prim. Atunci rezulta ca exista un j,
1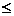 j
j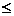 s, astfel incat p sa divida pe
s, astfel incat p sa divida pe 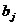 , ceea ce contrazice ipoteza.
, ceea ce contrazice ipoteza.
Sa
observam ca, deoarece in inelele factoriale orice element ireductibil
este prim, rezulta ca inelul 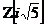 nu este
factorial. Se poate insa arata cu usurinta, prin
inductie dupa norma elementelor ca orice element nenul si
neinversabil din acest inel este produs de elemente ireductibile, incat
aceasta conditie nu este suficienta ca un inel sa fie
factorial. Iata un exemplu de doua descompuneri dinstincte in produs
de elemente ireductibile ale elementului 21 in inelul
nu este
factorial. Se poate insa arata cu usurinta, prin
inductie dupa norma elementelor ca orice element nenul si
neinversabil din acest inel este produs de elemente ireductibile, incat
aceasta conditie nu este suficienta ca un inel sa fie
factorial. Iata un exemplu de doua descompuneri dinstincte in produs
de elemente ireductibile ale elementului 21 in inelul 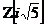 :
:
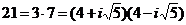
Pentru
inelele factoriale avem insa urmatoarea teorema.
Teorema 7. Daca A este un
inel factorial, atunci  este un inel
factorial.
este un inel
factorial.
Pentru
demonstrarea acestei teoreme avem nevoie de cateva pregatiri.
Daca
A este inel integru si  inelul
polinoamelor de o nedeterminata cu coeficientii in A , atunci,
dupa cum stim,
inelul
polinoamelor de o nedeterminata cu coeficientii in A , atunci,
dupa cum stim,  este inel
integru, iar elementele inversabile din
este inel
integru, iar elementele inversabile din  sunt cele din A
si numai ele. De aici rezulta ca doua polinoame din
sunt cele din A
si numai ele. De aici rezulta ca doua polinoame din  sunt asociate
daca si numai daca se obtin unul din celalalt prin
inmultire cu un element inversabil din A. Un element a
sunt asociate
daca si numai daca se obtin unul din celalalt prin
inmultire cu un element inversabil din A. Un element a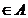 divide un polinom din
divide un polinom din daca si numai daca toti coeficientii polinomului se
divid cu a.
daca si numai daca toti coeficientii polinomului se
divid cu a.
Lema 8. Fie
A un inel integru si p un element prim in A. Atunci p este element prim
si in inelul
Demonstratie. Avem p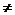 0 si p neinversabil in
0 si p neinversabil in  . Fie p|fg cu f, g
. Fie p|fg cu f, g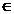
 .
Va trebui sa aratam ca p divide pe f sau pe g. Sa
presupunem ca p nu divide nici pe f nici pe g si aratam
ca atunci p nu divide nici produsul fg. Fie
.
Va trebui sa aratam ca p divide pe f sau pe g. Sa
presupunem ca p nu divide nici pe f nici pe g si aratam
ca atunci p nu divide nici produsul fg. Fie
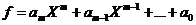
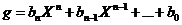
Deoarece p nu divide pe f,
rezulta ca exista 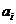 ,0
,0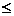 i
i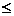 m, care nu se divide cu p. Fie
m, care nu se divide cu p. Fie 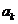 coeficientul lui
f cu k, pentru care
coeficientul lui
f cu k, pentru care 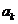 nu se divide cu
p. Analog, pentru g exista
nu se divide cu
p. Analog, pentru g exista 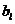 ,0
,0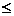 l
l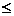 m,, cu l minim, pentru care
m,, cu l minim, pentru care 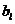 nu se divide cu
p. Atunci coeficientul
nu se divide cu
p. Atunci coeficientul 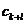 al produsului fg este egal cu
al produsului fg este egal cu
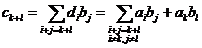
si se
observa ca 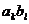 nu se divide cu
p(caci p este prim in A), iar prima suma se divide cu p, caci
fiecare termen contine un
nu se divide cu
p(caci p este prim in A), iar prima suma se divide cu p, caci
fiecare termen contine un 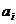 cu i <k sau
cu i <k sau 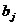 cu j<l sau suma este
zero. Asadar p nu divide pe
cu j<l sau suma este
zero. Asadar p nu divide pe 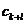 si nici pe fg.
si nici pe fg.
Fie
A un inel integru si f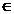
 .
Se spune ca f este un polinom primitiv daca coeficientii lui f
nu se divid cu acelasi element prin din A. Daca A este inel
factorial, se noteaza cu c(f) cel mai mare divizor comun al coeficientilor
lui f care exista dupa cum rezulta din lema 5 (c(f) se
numeste continutul polinomului f). Polinomul f va fi primitiv daca
si numai daca c(f)=1. Evident, orice polinom f
.
Se spune ca f este un polinom primitiv daca coeficientii lui f
nu se divid cu acelasi element prin din A. Daca A este inel
factorial, se noteaza cu c(f) cel mai mare divizor comun al coeficientilor
lui f care exista dupa cum rezulta din lema 5 (c(f) se
numeste continutul polinomului f). Polinomul f va fi primitiv daca
si numai daca c(f)=1. Evident, orice polinom f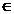
 se scrie sub forma f= c(f)f', unde f' este un polinom primitiv.
se scrie sub forma f= c(f)f', unde f' este un polinom primitiv.
Lema 9. Daca A este un inel
factorial si f,g sunt doua polinoame in  , atunci c(fg) este asociat cu c(f)c(g). In particular,
produsul a doua polinoame primitive este polinom primitiv.
, atunci c(fg) este asociat cu c(f)c(g). In particular,
produsul a doua polinoame primitive este polinom primitiv.
Demonstratie.
Fie f= c(f)f' si g= c(g)g'. Atunci fg= c(f)c(g)f'g' si este suficient
sa demonstram doar partea a doua a lemei. Fie f si g polinoame
primitive. Daca produsul f ar fi polinom primitiv, ar exista un element
prim p din A care sa divida produsul fg. Atunci, conform lemei
precedente, rezulta ca p divide pe f sau p divide pe g, absurd.
Lema 10. Fie A un inel factorial, a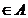 a
a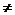 0, g
0, g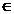
 ,
cu polinom primitiv. Daca g divide produsul af, atunci g divide pe f. In
particular, daca pentru doua polinoame primitive f,g din
,
cu polinom primitiv. Daca g divide produsul af, atunci g divide pe f. In
particular, daca pentru doua polinoame primitive f,g din  avem
relatia ag=bf cu a,b
avem
relatia ag=bf cu a,b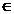
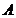 ,
b
,
b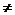 0, atunci f si g sunt asociate.
0, atunci f si g sunt asociate.
Demonstratie.
Din faptul ca g divide produsul af rezulta ca exista g'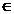
 astfel ca af=gg'. Aplicand lema precedenta, obtinem ca
ac(f)=c(g') (deoarece c(g)=1), de unde rezulta afirmatia lemei.
astfel ca af=gg'. Aplicand lema precedenta, obtinem ca
ac(f)=c(g') (deoarece c(g)=1), de unde rezulta afirmatia lemei.
Lema 11. Fie A un inel factorial
si f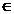
 cu grad f
cu grad f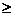 1. Atunci urmatoarele afirmatii sunt
echivalente:
1. Atunci urmatoarele afirmatii sunt
echivalente:
a)
f
este ireductibil in  ;
;
b)
f
este primitiv si ireductibil in 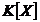 , unde K este corpul de fractii al lui A.
, unde K este corpul de fractii al lui A.
Demonstratie.
a) 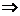 b). Daca f este ireductibil in
b). Daca f este ireductibil in  , atunci f este polinom primitiv. Sa presupunem
ca f ar fi ireductibil in
, atunci f este polinom primitiv. Sa presupunem
ca f ar fi ireductibil in 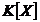 . Atunci ar exista, o descompunere a lui f de forma
f=gh, cu 1
. Atunci ar exista, o descompunere a lui f de forma
f=gh, cu 1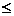 grad g<grad f, g,h
grad g<grad f, g,h 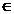
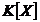 ,
de unde inmultind cu un element convenabil a
,
de unde inmultind cu un element convenabil a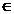 A, a
A, a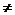 0 (a poate fi luat egal cu produsul tuturor numitorilor
coeficientilor polinoamelor g si h, obtinem in
0 (a poate fi luat egal cu produsul tuturor numitorilor
coeficientilor polinoamelor g si h, obtinem in  o relatie
de forma af=g'h', cu grad g'=grad g si grad h'=grad h. Fie g'=c(g')g
o relatie
de forma af=g'h', cu grad g'=grad g si grad h'=grad h. Fie g'=c(g')g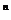 . Atunci rezulta ca g'' divide pe f in
. Atunci rezulta ca g'' divide pe f in  (lema 10)
si deoarece grad g
(lema 10)
si deoarece grad g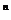 =grad g, rezulta ca f este reductibil in
=grad g, rezulta ca f este reductibil in  impotriva
ipotezei.
impotriva
ipotezei.
Implicatia b) 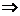 a) este evidenta.
a) este evidenta.
Lema 12. Daca A este un inel
factorial orice polinom ireductibil din  este prim.
este prim.
Demonstratie.
Fie f un polinom ireductibil din . Daca grad f=o, atunci f este element ireductibil
in A, deci prim in A si deci prim si in
. Daca grad f=o, atunci f este element ireductibil
in A, deci prim in A si deci prim si in  , conform lemei 8. Daca grad f>0, atunci rezulta ca f este polinom primitiv si sa presupunem ca f
divide produsul gh. Din lema precedenta rezulta ca f este
element prim in
, conform lemei 8. Daca grad f>0, atunci rezulta ca f este polinom primitiv si sa presupunem ca f
divide produsul gh. Din lema precedenta rezulta ca f este
element prim in 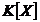 ,
deci f divide in
,
deci f divide in 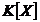 unul dintre
polinoamele g sau h. S a presupunem
ca f|g. Deci g=ff', unde f'
unul dintre
polinoamele g sau h. S a presupunem
ca f|g. Deci g=ff', unde f' 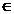
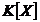 .
Atunci exista a
.
Atunci exista a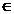 A, a
A, a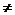 0, astfel incat af'
0, astfel incat af'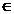
 .
Rezulta ca f divide pea g in
.
Rezulta ca f divide pea g in  si din lema
10 deducem ca f divide pe g in
si din lema
10 deducem ca f divide pe g in  .
.
Ne
intoarcem sa demonstram teorema 6 Vom verifica conditia b) din
teorema 3. Pentru aceasta, conform lemei precedente, va fi suficient sa
aratam ca orice element neinversabil si nenul din  , este produs finit de polinoame ireductibile.
Daca f este polinom de grad zero neinversabil, atunci el este produs finit de elemente prime in A care
sunt prime deci si ireductibile in
, este produs finit de polinoame ireductibile.
Daca f este polinom de grad zero neinversabil, atunci el este produs finit de elemente prime in A care
sunt prime deci si ireductibile in  conform lemei 8.
Daca grad f>1, f se scrie sub forma f=c'(f)f', unde
f' este un polinom primitiv, si este suficient sa demonstram
afirmatia pentru polinoamele primitive. Deci daca f este primitiv
si ireductibil, afirmatia este evidenta. In caz contrat f=gh,
unde g si h sunt polinoame de grad strict mai mic decat cel al lui f
si din ipoteza inductiva rezulta afirmatia.
conform lemei 8.
Daca grad f>1, f se scrie sub forma f=c'(f)f', unde
f' este un polinom primitiv, si este suficient sa demonstram
afirmatia pentru polinoamele primitive. Deci daca f este primitiv
si ireductibil, afirmatia este evidenta. In caz contrat f=gh,
unde g si h sunt polinoame de grad strict mai mic decat cel al lui f
si din ipoteza inductiva rezulta afirmatia.
Din teorema demonstrata
rezulta:
Corolarul
13. Daca A este inel factorial, atunci 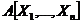 ,
inelul polinoamelor de n nedeterminate cu coeficientii in A , este
factorial. In particular, orice inel de polinoame de n nedeterminate cu
coeficienti intr-un corp este inel factorial.
,
inelul polinoamelor de n nedeterminate cu coeficientii in A , este
factorial. In particular, orice inel de polinoame de n nedeterminate cu
coeficienti intr-un corp este inel factorial.
Din
teorema 7 si teorema 3 rezulta ca pentru inelul factorial A in
innelul  exista cel
mai mare divizor comun a doua
elemente. Insa putem sa observam ca propozitia 3.4 nu
mai ramane in general valabila. Astfel in inelul
exista cel
mai mare divizor comun a doua
elemente. Insa putem sa observam ca propozitia 3.4 nu
mai ramane in general valabila. Astfel in inelul 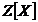 idealul generat de 2 si X, adica idealul 2
idealul generat de 2 si X, adica idealul 2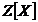 +X
+X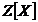 este diferit de
este diferit de 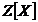 ( v.
demonstratia propozitiei 3.3.), insa 1 este evident cel mai mare
divizor comun al lui 2 si X.
( v.
demonstratia propozitiei 3.3.), insa 1 este evident cel mai mare
divizor comun al lui 2 si X.
Cu
ajutorul rezultatelor de mai sus vom demonstra doua criterii de
ireductibilitate a polinoamelor de o nedeterminata, cu coeficienti
intr-un corp.
Propozitia 1 (Criteriul lui
Eisenstien). Fie A un inel factorial, K corpul sau de fractii, 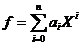 un polinom de grad n>1
din
un polinom de grad n>1
din  si p un element prim in A cu
proprietatile:
si p un element prim in A cu
proprietatile: 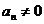 mod p,
mod p,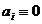 mod p pentru i <n si
mod p pentru i <n si 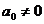 mod p
mod p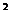 . Atunci f este polinom ireductibil in
. Atunci f este polinom ireductibil in 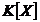 , si deci si in
, si deci si in  daca este
primitiv.
daca este
primitiv.
Demonstratie.
Putem presupune ca f este polinom primitiv. Atunci daca f este
ireductibil in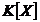 , el este reductibil in
, el este reductibil in  . Fie f=gh, g, h
. Fie f=gh, g, h 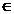

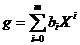
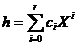
Unde 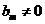 ,
, 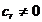 ,
,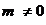 ,
,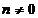 . Din
. Din 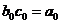 si
si 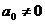 mod pentru p
mod pentru p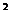 rezulta ca unul si numai unul dintre
elementele
rezulta ca unul si numai unul dintre
elementele  si
si 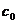 se divide cu p. Presupunem ca
se divide cu p. Presupunem ca 
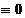 mod p si
mod p si 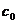
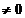 mod p. Intrucat
mod p. Intrucat 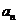
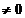 mod p , nu
toti coeficientii lui g se divid cu p. Deci exista un indice I
minim, cu proprietatea ca
mod p , nu
toti coeficientii lui g se divid cu p. Deci exista un indice I
minim, cu proprietatea ca 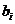 nu se divide cu p.
Atunci
nu se divide cu p.
Atunci 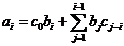 nu se divide cu
p, ceea ce contrazice ipoteza.
nu se divide cu
p, ceea ce contrazice ipoteza.
Propozitia 15. Fie u:A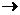 B un morfism de inele integre cu A inel factorial, K
corpul de fractii al lui A si L corpul de fractii al lui B.
Notam cu u' morfismul
B un morfism de inele integre cu A inel factorial, K
corpul de fractii al lui A si L corpul de fractii al lui B.
Notam cu u' morfismul 
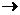
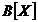 , cu proprietatea ca u'(X)=(X) si care
extinde pe u. Atunci daca f
, cu proprietatea ca u'(X)=(X) si care
extinde pe u. Atunci daca f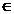
 este astfel incat u'(f) este ireductibil in
este astfel incat u'(f) este ireductibil in 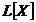 iar grad f=
u'(f), rezulta ca f este ireductibil in
iar grad f=
u'(f), rezulta ca f este ireductibil in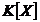
Demonstratie.
Putem presupune ca f este primitiv . Atunci, daca presupunem ca
f este reductibil in 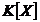 , el este reductibil si in
, el este reductibil si in  . Fie f=gh, cu grad g
. Fie f=gh, cu grad g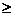 1, grad h
1, grad h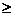 1. Atunci u'(f) =u'(g) u'(h) si
rezulta grad u'(g)= grad g, iar grad u'(h)=grad h, ceea ce contrazice
faptul ca u'(f) este ireductibil,
1. Atunci u'(f) =u'(g) u'(h) si
rezulta grad u'(g)= grad g, iar grad u'(h)=grad h, ceea ce contrazice
faptul ca u'(f) este ireductibil,

