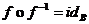Multimi,
relatii, functii
In cele ce
urmeaza, nu vom insista asupra teoriei axiomatice a multimilor, ea
nefiind scopul acestei lucrari.
Prin multime, vom intelege, simplu,
o colectie de obiecte de un acelasi tip, obiectele fiind numite elementele multimii. Se presupune
ca, in momentul abordarii acestui text, cititorul are
cunostintele necesare parcurgerii acestui paragraf, scopul sau
fiind, in principal, sa fixeze o serie de
notatii si sa reaminteasca o serie de rezultate care nu pot
fi gasite cu usurinta in alta parte.
Multimile vor fi
notate, in general, cu litere mari din alfabetul latin, A, B, C, . , iar elementele lor cu a, b,
c, . . Cardinalul lui A
(numarul de elemente ale lui A),
il notam |A|.
Fie doua
multimi, A si B.
Spunem ca A este submultime a lui B
si scriem A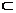 B (sau B
B (sau B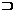 A) daca
orice element a lui A este si
element a lui B.
A) daca
orice element a lui A este si
element a lui B.
Spunem ca A si B sunt egale si
scriem A = B daca A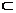 B si B
B si B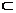 A.
A.
Daca A si B nu sunt egale, scriem A
≠ B.
Spunem ca A este o submultime proprie a lui B
daca A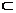 B, cu A ≠ B.
B, cu A ≠ B.
Multimea care nu
contine nici un element se numeste multimea vida si este notata cu Ø.
Multimea
vida poate fi caracterizata astfel : Ø = .
Vom numi intersectia multimilor A si B, multimea de elemente care apartine atat lui A, cat si lui B si o notam cu A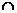 B.
B.
Daca A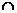 B = Ø, se spune
ca A si B sunt disjuncte.
B = Ø, se spune
ca A si B sunt disjuncte.
Se numeste reuniuna lui A si B multimea
notata cu A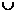 B, ale carei
elemente apartin cel putin uneia dintre multimile A si B.
B, ale carei
elemente apartin cel putin uneia dintre multimile A si B.
Se numeste diferenta multimilor A si B si se noteaza cu A
- B multimea
Atunci cand toate
multimile considerate sunt submultimi ale unei aceleiasi
multimi X, vom nota
diferenta X - A cu C(A) si o vom numi o complementara a lui A.
Produsul cartezian al multimilor A si B, notat cu A 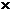 B este multimea perechilor ordonate (a, b), unde a
B este multimea perechilor ordonate (a, b), unde a A si b
A si b B, A
B, A 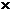 B
= .
B
= .
Daca 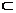 A
A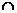 B, a ≠ b,
atunci perechile (a, b) si (b, a)
sunt elemente distincte ale lui A
B, a ≠ b,
atunci perechile (a, b) si (b, a)
sunt elemente distincte ale lui A 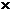 B
B
Acest lucru se
exprima spunand ca A 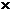 B este multimea perechilor ordonate.
B este multimea perechilor ordonate.
Definitia produsului cartezian se poate
extinde la n multimi A1,
A2, . , An,
A1 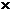 A2
A2
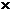 .
.
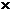 An
= ,
An
= ,
unde 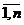 =
=
In cazul in care A1 = A2 = . = An
= A vom nota produsul cartezian cu An.
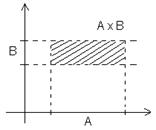
In cazul in care A si B sunt intervale din R,
A 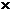 B se poate vizualiza usor:
B se poate vizualiza usor:
O
multime distinsa asociata oricarei multimi A este multimea
partilor lui A,
notata P(A)
si se defineste ca fiind multimea tuturor submultimilor lui
A. Asadar, P(A) = . Vom nota prin P*(A)
multimea P(A) din care s-a extras multimea vida, Ø. Merita sa
mentionam aici ca |P(A)| = 2|A|
Definitie
1.1. Date
doua multimi A si B, se numeste relatie de la A la B, orice submultime a produsului cartezian
A 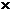 B.
B.
Daca R este o relatie de la A la B, vom nota (x, y) R si in
felul urmator xRy.
R si in
felul urmator xRy.
Daca o
relatie are proprietatea (a, b), (a,
c)  R, atunci b = c.
R, atunci b = c.
Se numeste domeniu lui R urmatoarea submultime a lui A :
D(R) =
.
Se numeste codomeniu lui R urmatoarea
submultime a lui B :
C(R) = .
Definitie 1.2. Se numeste functie multivoca de la multimea A la multimea B, o relatie a carei domeniu coincide cu A.
Pentru orice
multime A vom numi relatie pe A o relatie de la A
la A.
O relatie
particulara pe A este relatia identitate a lui A (sau diagonala):
IA
= .
Se observa
ca IA este o
functie multivoca.
Definitie 1.3. Fie R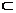 A
A 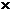 A.
A.
- R se numeste reflexiva
daca
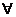 x
x A, (x, x)
A, (x, x) R;
R;
- R se numeste simetrica
daca pentru orice (x, y)
 R, avem
si (y, x)
R, avem
si (y, x) R;
R;
- R se numeste tranzitiva
daca pentru orice (x, y)
 R si (y, z)
R si (y, z) R, avem
ca (x, z)
R, avem
ca (x, z) R;
R;
- R se numeste antisimetrica
daca pentru orice (x, y)
 R si (y, x)
R si (y, x) R, avem x = y.
R, avem x = y.
O relatie R pe A,
care este reflexiva, simetrica si tranzitiva se
numeste relatie de
echivalenta pe A.
O relatie R pe A,
care este reflexiva si tranzitiva se numeste relatie de preordine pe A.
O relatie R pe A,
care este reflexiva, antisimetrica si tranzitiva se
numeste relatie de ordine
partiala pe A.
Cuplul (A, R) = multime partial
ordonata.
Daca R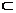 A
A 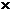 B, notam cu R-1
relatia de la B la A,numita inversa relatiei R,
definita astfel:
B, notam cu R-1
relatia de la B la A,numita inversa relatiei R,
definita astfel:
R-1 =
.
Daca R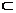 A × B si S
A × B si S 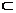 B × C,
notam cu S ◦ R
relatia de la A la C definita astfel :
B × C,
notam cu S ◦ R
relatia de la A la C definita astfel :
S◦R = ,
pe care o numim compunerea (produsul) relatiilor R
si S.
Observatii 1.4.
- R este reflexiva daca R
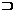 IA
IA
- R este simetrica daca R
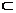 R-1 (chiar R = R-1);
R-1 (chiar R = R-1);
- R este tranzitiva daca R◦R
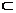 R;
R;
- R este antisimetrica daca R
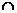 R-1
R-1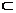 IA
IA
Definitie 1.5. Fie 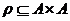 o
relatie de echivalenta. Se numeste clasa de echivalenta a elementului
o
relatie de echivalenta. Se numeste clasa de echivalenta a elementului 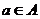 multimea
multimea 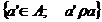 . Clasa de echivalenta a lui a se noteaza
. Clasa de echivalenta a lui a se noteaza 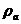 sau
sau 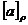 sau a.
sau a.
Exemple 1.6.
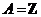
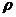 este congruenta modulo n,
este congruenta modulo n, 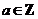 . Clasa de echivalenta a lui
. Clasa de echivalenta a lui 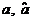 cuprinde toate numerele intregi care dau acelasi rest ca si a la impartirea prin n.
cuprinde toate numerele intregi care dau acelasi rest ca si a la impartirea prin n.
Fie 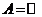
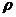 relatia din exemplul 1.1, 10.
Sa observam ca doua numere reale sunt echivalente daca
si numai daca au aceeasi parte fractionara. (se
stie ca orice
relatia din exemplul 1.1, 10.
Sa observam ca doua numere reale sunt echivalente daca
si numai daca au aceeasi parte fractionara. (se
stie ca orice 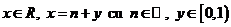 ,
y numindu-se partea fractionara a lui x). Asadar, intr-o clasa de echivalenta se
regasesc toate numerele reale avand aceeasi parte
fractionara.
,
y numindu-se partea fractionara a lui x). Asadar, intr-o clasa de echivalenta se
regasesc toate numerele reale avand aceeasi parte
fractionara.
Definitie 1.7. Fie A
o multime si P = i I o
familie de submultimi ale lui A. P
se numeste partitie a lui A daca satisface conditiile :
I o
familie de submultimi ale lui A. P
se numeste partitie a lui A daca satisface conditiile :
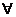 i
i I, Ai ≠ Ø;
I, Ai ≠ Ø;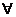 i,j
i,j I, i ≠ j
I, i ≠ j 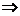 Ai
Ai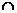 Aj = Ø;
Aj = Ø;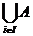 i =
A.
i =
A.
Observatii 1.8.
10 Orice relatie de
echivalenta 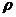 pe A
determina o partitie a lui A, submultimile
pe A
determina o partitie a lui A, submultimile
partitiei fiind clasele de
echivalenta.
20 Daca 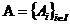 este o partitie a lui A, putem defini relatia
asociata partitiei:
este o partitie a lui A, putem defini relatia
asociata partitiei:
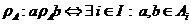
Dupa cum se constata usor, 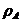 este o relatie de echivalenta
pe A.
este o relatie de echivalenta
pe A.
In plus, daca 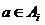 , clasa sa de echivalenta,
, clasa sa de echivalenta, 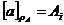
Daca 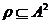 , este o echivalenta,
multimea claselor de echivalenta ale lui A
, este o echivalenta,
multimea claselor de echivalenta ale lui A
relativ la 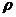 se numeste
multimea cat (sau factor) a
lui A relativ la
se numeste
multimea cat (sau factor) a
lui A relativ la 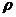 si se
si se
noteaza 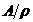 . Aplicatia
. Aplicatia 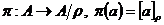 se numeste aplicatia
se numeste aplicatia
canonica sau proiectia canonica.
Fie 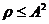 o
relatie oarecare.
o
relatie oarecare.
In cele ce
urmeaza vom incerca sa determinam cea mai mica (in sensul
incluziunii de multimi) relatie de echivalenta pe A care contine 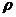 , adica relatia de echivalenta generata de
, adica relatia de echivalenta generata de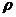 . Daca o vom nota, pentru
moment, prin
. Daca o vom nota, pentru
moment, prin 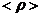 , este clar ca
, este clar ca 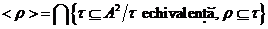 . Aceasta definitie nu este
foarte utila din punct de vedere practic, ea este insa folositoare
atunci cand este vorba de minimalitatea ei. Putem insa sa o construim
efectiv:
. Aceasta definitie nu este
foarte utila din punct de vedere practic, ea este insa folositoare
atunci cand este vorba de minimalitatea ei. Putem insa sa o construim
efectiv:
Definitie 1.9.
Relatia 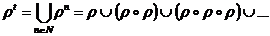 se numeste inchiderea tranzitiva a relatiei
se numeste inchiderea tranzitiva a relatiei 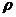
Sa observam
ca 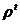 este o relatie tranzitiva si,
in plus, este inclusa in orice relatie tranzitiva ce
contine
este o relatie tranzitiva si,
in plus, este inclusa in orice relatie tranzitiva ce
contine 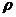
Fie 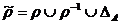 . Aceasta relatie este, evident,
reflexiva si simetrica, si este cea mai mica
relatie (in sensul incluziunii) relatie cu aceste
proprietati ce include
. Aceasta relatie este, evident,
reflexiva si simetrica, si este cea mai mica
relatie (in sensul incluziunii) relatie cu aceste
proprietati ce include 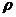
Din acest moment este
clar ca avem:
Propozitie 1.10. Relatia de echivalenta
generata de 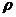 este
este 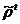 (inchiderea tranzitiva a lui
(inchiderea tranzitiva a lui 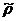 ). In plus,
). In plus, 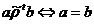 sau exista sirul de elemente din
sau exista sirul de elemente din 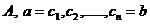 astfel incat
astfel incat 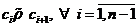 (sau, echivalent,
(sau, echivalent, 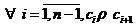 sau
sau 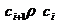
Definitie 1.11. Fie A
o multime, 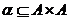 o
relatie de echivalenta peste A.
O submultime B a lui A se numeste α - saturata
daca
o
relatie de echivalenta peste A.
O submultime B a lui A se numeste α - saturata
daca 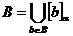
Propozitie 1.12. In ipotezele precedente, B este α -
saturata daca si numai daca
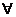
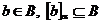
Demonstratie :
 este evidenta.
este evidenta.
 Deoarece
Deoarece 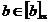 rezulta ca
rezulta ca 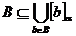 . Din ipoteza,
. Din ipoteza, 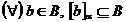 , deci
, deci 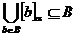 , deci avem egalitatea ceruta.
, deci avem egalitatea ceruta.
Definitie 1.13. Un sistem
de inchidere este o familie de parti C P(M) cu proprietatile :
P(M) cu proprietatile :
- 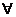 D, D
D, D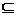 C ,
C , 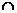
 C
C
- M C
C
Definitie 1.14. Un operator
de inchidere pe o multime M
este o aplicatie
c : P(M)→P(M) cu proprietatile:
- M1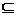 M2
M2 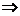 c(M1)
c(M1) 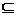 c(M2)
c(M2) 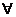 M1, M2
M1, M2 P(M);
P(M);
-M1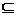 c(M1)
c(M1) 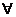 M1
M1 P(M);
P(M);
-c(c(M1))
= c(M1) 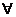 M1
M1 P(M).
P(M).
Definitie 1.15. Fie A,
B doua multimi. Se
numeste functie de la A la B o
relatie 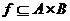 definita prin urmatoarele conditii:
definita prin urmatoarele conditii:
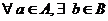 astfel incat
astfel incat 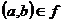
20 Daca 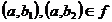 atunci
atunci 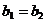
Sau, o aplicatie sau o functie f de la o
multime A la o multime B este o functie multivoca ce satisface conditia : [xfy, yfz]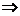 y = z.
y = z.
In cazul in care se
slabesc conditiile din definitie, se pot obtine
notiuniunile de functie
partiala (care nu este peste tot definita - slabirea
conditiei 10) si functie
multivaluata sau functie
nedeterminista ( dispare conditia 20).
Faptul ca
perechea (a,b) apartine functiei f
se noteaza 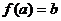 . In general, o functie
. In general, o functie 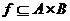 se noteaza prin
se noteaza prin 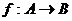 sau
sau 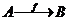 . Oricarei functii
. Oricarei functii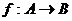 i se poate asocia o relatie, graficul functiei
i se poate asocia o relatie, graficul functiei 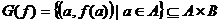
Pentru doua
functii , se poate vorbi despre compunerea
lor ca relatii:
f : A→B si g : B →C, f ◦ g = .
Dupa cum se poate
constata usor, compunerea a doua functii este si ea, la
randul ei, o functie.
Avand in vedere ca,
in definirea lui f ◦ g, (a, c) f ◦ g daca si numai daca
f ◦ g daca si numai daca 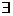 b
b B astfel incat
f(a) = b si g(b) = c, putem scrie ca
g(f(a)) = c, ceea ce justifica o conventie de notatie: in
loc de 'f ◦ g' vom
scrie'g ◦ f',
adica in loc sa scriem (f
◦ g)(a) = c, vom scrie
B astfel incat
f(a) = b si g(b) = c, putem scrie ca
g(f(a)) = c, ceea ce justifica o conventie de notatie: in
loc de 'f ◦ g' vom
scrie'g ◦ f',
adica in loc sa scriem (f
◦ g)(a) = c, vom scrie
(g ◦ f)(a) = g(f(a)) = c.
Definitie1.16. Fie functia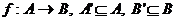
10 Se numeste domeniul lui f - multimea A
20 Se numeste codomeniul lui f - multimea B
30 Se numeste imaginea lui A' prin f - multimea 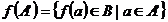
40 Se numeste contraimaginea lui B' prin f
- multimea 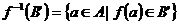
50 Se numeste restrictia lui f la A' - functia 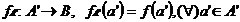
60 Daca 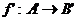 este o functie astfel incat
este o functie astfel incat 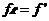 se spune ca f ' s-a prelungit la A
sau, inca, ca f este o prelungire a lui f ' la A.
se spune ca f ' s-a prelungit la A
sau, inca, ca f este o prelungire a lui f ' la A.
Observatie 1.17. Sa remarcam ca, in
definitia anterioara, la punctul 40, nu este vorba de
functia inversa. Este vorba de relatia inversa, intrucat
relatia inversa a unei functii poate sa nu fie
functie.
Definitie
1.18. Fie f : A → B o functie.
f se numeste functie
injectiva daca din f(a) =
f(b) rezulta ca a = b
(sau 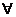 a, b
a, b A cu a ≠ b
A cu a ≠ b 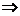 f(a) ≠ f(b)).
f(a) ≠ f(b)).
f
se numeste functie
surjectiva daca f(A) = B (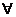 b
b B,
B, 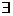 a
a A astfel incat
A astfel incat
f(a) = b).
f se numeste functie bijectiva
daca este injectiva si surjectiva (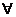 b
b B,
B, 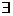 !a
!a A astfel incat f(a) = b).
A astfel incat f(a) = b).
Observatii 1.19. Fie 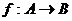 o
functie.
o
functie.
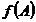 se mai noteaza
se mai noteaza 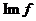 si se numeste imaginea functiei f.
si se numeste imaginea functiei f.
Se poate demonstra fara
dificultate ca f este
bijectiva daca si numai daca
relatia inversa, 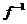 , este si ea functie.
, este si ea functie.
Daca A este o multime, 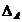 este chiar functie, si se
numeste functia identitate
este chiar functie, si se
numeste functia identitate
pe A,
notata 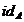 . Daca f este bijectiva atunci
. Daca f este bijectiva atunci 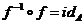 si
si