Radacinile polinoamelor. Teorema
lui Bézout.
Definitia Fie
f un polinom nenul cu coeficienti complecsi. Un numar
complex, 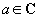 se numeste radacina a polinomului
f daca f (a) = 0 .
se numeste radacina a polinomului
f daca f (a) = 0 .
Exemple
Numarul
2 este radacina pentru polinomul 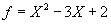 pentru ca f (2) = 0.
pentru ca f (2) = 0.
Numarul i este radacina
pentru polinomul 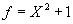 pentru ca
pentru ca 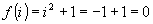 .
.
Observatie: Pentru a afla radacinile unui polinom f
se rezolva ecuatia f (x) = 0 ; spre exemplu, pentru a
afla radacinile polinomului 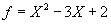 vom rezolva
ecuatia
vom rezolva
ecuatia 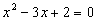 si
gasim radacinile polinomului
si
gasim radacinile polinomului 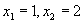 .
.
Teorema lui Bézout: Fie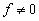 un polinom
nenul. Numarul
un polinom
nenul. Numarul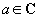 este
radacina a polinomului f daca si numai
daca X - a divide f .
este
radacina a polinomului f daca si numai
daca X - a divide f .
Exemplu
Polinomul 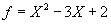 avand radacinile
avand radacinile 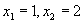 se va divide atat prin X - 1 cat si
prin
se va divide atat prin X - 1 cat si
prin
X

