Reprezentarea sistemelor dinamice liniare prin functii de
transfer
Obiectiv:
Evidentierea modelelor de tip functie de transfer. Calcularea
raspunsurilor sistemelor dinamice liniare - analitic si in Matlab.
Breviar teoretic
Raspunsul in domeniul timp
Un
sistem dinamic liniar, continuu si invariant in timp,
actionat prin marimea de intrare u(t) si avand marimea de
iesire y(t), poate fi descris printr-un model matematic de tip ecuatie
diferentiala liniara de ordinul n, cu coeficienti constanti si
reali
 . (1)
. (1)
O descriere
echivalenta a sistemului, pentru CONDITII INITIALE NULE:
 si
si  , este prin functia de transfer:
, este prin functia de transfer:
 , (2)
, (2)
unde Y(s)
si U(s) sunt transformatele Laplace ale semnalelor y(t) si
u(t),
iar P(s) si Q(s) sunt polinoame cu coeficienti
reali, de variabila complexa.
Pentru sisteme strict realiste (care
exista in realitate)  . Daca aceasta conditie nu este
indeplinita, nu se poate gasi un sistem real corespunzator
acestui model.
. Daca aceasta conditie nu este
indeplinita, nu se poate gasi un sistem real corespunzator
acestui model.
Radacinile
polinomului P(s) se numesc polii sistemului. Radacinile lui Q(s)
se numesc zerourile
sistemului.
Raspunsul in domeniul timpului al sistemului descris de (1), (2) reprezinta iesirea y(t),
t ≥ 0, calculata
pentru u(t) cunoscut in domeniul t ≥ 0.
In studiul sistemelor
intervin raspunsuri tipice, definite pentru forme particulare ale semnalului de intrare:
a)Raspunsul indicial -
raspunsul sistemului (1), (2) in domeniul timpului, pentru conditii
initiale nule si semnal de intrare de tip treapta unitara.
b)Raspunsul la impuls - raspunsul
sistemului (1), (2) in domeniul timpului, pentru conditii initiale
nule si semnal de intrare de tip impuls Dirac.
c)Raspunsul la semnal sinusoidal -
raspunsul sistemului(1), (2) in domeniul timpului pentru conditii
initiale nule si un semnal de
intrare sinusoidal de tipul 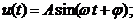
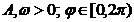 .
.
Evident raspunsul
in domeniul timpului poate fi determinat analitic, deci ca o functie
explicita de timp pentru t ≥ 0.
1.1 Metoda analitica de calcul al
raspunsului
Pe
baza modelului tip (1)
Se rezolva
ecuatia diferentiala de tip 1
Pe
baza functiei de transfer
Se foloseste
transformata Laplace:
Pasul 1 Se determina transformata
Laplace a raspunsului sistemului: 
Pentru calculul lui U(s) prezentam mai jos un tabel de
transformate Laplace:


Pasul 2 Se descompune Y(s) in fractii simple si se
calculeaza constantele ce intervin la numaratorul
fractiilor simple.
Se noteaza  , unde M(s) si
N(s) sunt polinoame de variabila
complexa, cu coeficienti reali.
, unde M(s) si
N(s) sunt polinoame de variabila
complexa, cu coeficienti reali.
Fractiile simple
se aleg dupa radacinile lui N(s),
astfel:
a) pentru o radacina
(notata p) de multiplicitate 1 ,
fractia simpla corespunzatoare este:
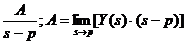 ;
;
b) pentru o radacina
(notata p) de multiplicitate  , fractiile simple corespunzatoare sunt:
, fractiile simple corespunzatoare sunt:
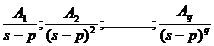 ;
;
unde:
 .
.
Daca N(s) are doua radacini
complexe, conjugate, de multiplicitate 1, acestea se pot grupa si
fractia simpla corespunzatoare lor este:
 ,
,
unde B
si C se obtin prin metoda
identificarii coeficientilor.
Pasul 3. Se
calculeaza y(t), folosind
inversa transformatei Laplace pentru Y(s)
obtinut ca suma de fractii simple. Este util in acest scop
tabelul 2.
Deoarece polinomul N(s)
are coeficienti reali, daca N(s) admite o radacina
complexa, atunci sigur admite si radacina complexa
conjugata. Se pot grupa in perechi termenii corespunzatori acestor
radacini si se pot opera prelucrari pe baza formulelor:
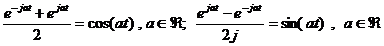 ,
,
asa cum se va
arata in exemplele urmatoare.
Observatie: Se obtine astfel raspunsul y(t)
pentru t >= 0; pentru t < 0 ,  pe baza principiului
cauzalitatii (
pe baza principiului
cauzalitatii ( pentru t < 0).
pentru t < 0).
2.
Exercitii rezolvate analitic
Sa se
calculeze raspunsurile indicial, la impuls si respectiv la intrarea  , pentru sistemele indicate mai jos.
, pentru sistemele indicate mai jos.
Rezolvare:
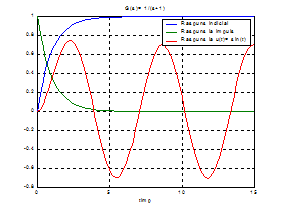
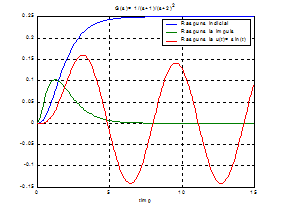
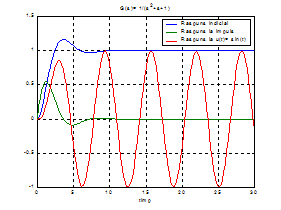
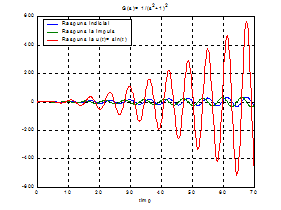
Raspunsurile calculate
analitic in cele ce urmeaza sunt indicate in fig. 1.
1)
Sistemul 1:
 .
.
a) Raspunsul 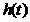 la intrarea
la intrarea 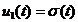 (numit
raspuns indicial)
(numit
raspuns indicial)
Pasul 1 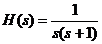 .
.
Pasul 2 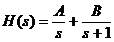 ,
,
unde: 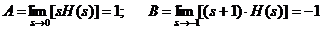 .
.
Se obtine: 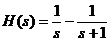 .
.
Pasul 3  .
.
Folosind tabelul 2, se obtine:  .
.
Rezulta ca:  .
.
b) Raspunsul la intrarea  (raspuns la
impuls)
(raspuns la
impuls)
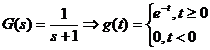 .
.
c) Raspunsul la intrarea 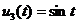
 ,
,
unde:

Se obtine:
 .
.
2) Sistemul
 .
.
Raspunsul la intrarea  (raspuns
la impuls)
(raspuns
la impuls)


Rezulta:


3) Sistemul 3:
 .
.
Raspunsul la intrarea  (numit raspuns
indicial)
(numit raspuns
indicial)
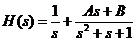
Prin metoda identificarii
coeficientilor se obtine:
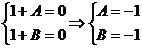 .
.
In concluzie, se poate scrie:
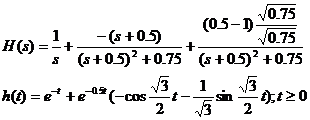
4) Sistemul 4:

Raspunsul la intrarea  (raspuns la impuls)
(raspuns la impuls)
 ,
,
unde:
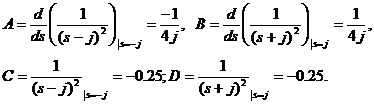 .
.
Se obtine:
 .
.
Fig. 1
Raspunsurile analizate la exercitiul 1
Observatii:
- daca sistemul are doar poli cu parte reala strict
negativa, raspunsul
sistemului va avea, dupa un anumit interval de timp (numit regim
tranzitoriu), o forma asemanatoare cu intrarea
(se spune ca sistemul admite un
regim permanent); pentru astfel de
sisteme raspunsul
indicial tinde la o constanta, raspunsul la impuls
tinde la zero.
- daca sistemul are poli complecsi, raspunsurile indicial si la impuls sunt oscilante;
daca sistemul are doar poli complecsi cu parte
reala strict negativa si, eventual, alti poli reali, cu
parte reala negativa, raspunsurile indicial si la impuls
sunt oscilante, amortizate.
- daca sistemul are
doar poli reali, raspunsul indicial si la impuls sunt aperiodice
3.
Simularea sistemelor dinamice liniare continue cu ajutorul MATLAB
Domeniul de
definitie al lui y(t) este intervalul (0, ). In Matlab, din intervalul continuu de valori ale timpului, pot fi
retinute un numar finit de valori:
t=[t1 t2 t3 tn].
Atunci marimile de intrare si de iesire vor fi reprezentate prin vectori de forma:
u=[u(t1) u(t2) u(t3)..u(tn)]=
[u1 u2 u3 ..un]
y=[y(t1) y(t2) y(t3)..y(tn)]=
[y1 y2 y3 ..yn]
Functiile
Matlab, care calculeaza si returneaza
iesirea sistemului pentru anumite intrari, solicita construirea
urmatorilor vectori:
doi vectori
necesari pentru descrierea in mod unic a sistemului modelat de (2):
- un vector corespunzator polinomului Q(s)
de la numaratorul functiei de transfer:
num
= [bm bm-1 . b0]
- un vector corespunzator polinomului P(s)
de la numitorul functiei de transfer:
den = [an an-1a0]
vectorul de
timp t care sa precizeze
momentele de timp la care este calculata iesirea sistemului:
t=[t1 t2 t3
tn]
vectorul de
intrare u la momentele de timp
indicate prin vectorul t:
u=[u(t1) u(t2) u(t3)..u(tn)]=
[u1 u2 u3
..un]
Daca intrarea
este de tip treapta sau impuls Dirac se recomanda folosirea functiilor
Matlab step, impulse care isi construiesc automat vectorii de intrare
necesari.
In general, punctele
din vectorul timp se plaseaza
echidistant in intervalul [tl , tn].
t=t1:p:tn = [t1
t2 t3 tn] = [t1 + 0*p t1 +p..t1+(n-1)*p],
unde
p
= pas de simulare
t1+(n-1)*p
= tn
Acesti vectori
vor fi argumente pentru functiile Matlab cu ajutorul carora se va
determina raspunsul in domeniul timpului pentru sistemele de tipul (2).
Functiile Matlab vor returna vectorul de iesire y=[y(t1) y(t2) ..y(tn)].
3.1 Indicatii asupra modului de alegere a
vectorului de timp
t=t1:p:tn = [t1
t2 t3 tn] = [t1 + 0*p t1 +p..t1+(n-1)*p],
unde
p=pas
de simulare
t1+(n-1)*p=tn.
Vectorul de iesire va fi
[y(t1) y(t2).y(tn)].
Simularea sistemelor
dinamice cu ajutorul MATLAB-ului solicita alegerea unui interval de timp marginit de simulare [t1, tn], cu t1 si tn
finiti, interval pe care se urmareste comportarea sistemului. In
acest interval se alege un numar finit de puncte
de simulare (puncte in care va avea loc esantionarea semnalelor),
in general echidistante. In acest caz, distanta dintre doua puncte de
simulare succesive se va numi pas de
simulare.
Trebuie stabilite lungimea
intervalului de simulare si pasul de simulare, in asa fel incat
simularea sa furnizeze toate informatiile importante despre iesirea
sistemului si sa nu fie consumatoare de timp.
- cu
cat numarul punctelor de simulare este mai mare, cu atat simularea va
evidentia mai bine comportarea sistemului real, fiind ilustrate toate
variatiile lui y(t); simularea va implica, in aceste
situatii, un consum mare de memorie si o viteza mica de
lucru, ca urmare a unui numar mult mai mare de calcule ce trebuie
efectuate.
- daca numarul de puncte de simulare
este prea mic, se pot obtine informatii eronate (incomplete) despre
evolutia sistemului.
Se pune problema de a
gasi un compromis acceptabil intre aceste doua tendinte
divergente. Pentru a nu denatura printr-un calcul numeric prost
conditionat raspunsul simulat fata de forma analitica se ofera
cateva sugestii de alegere a marimii intervalului de esantionare.
- pasul de esantionare p se alege in functie de polul de modul maxim, dupa formula:
 (3)
(3)
Pentru a explica aceasta formula trebuie amintit faptul
ca raspunsul sistemul in domeniul timpului este, de fapt, o
superpozitie de exponentiale de tipul:
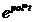 . (4)
. (4)
Raspunsul este corect obtinut, daca
variatia tuturor aceste exponentiale este surprinsa in
suficiente puncte.
Daca polul are parte reala strict negativa,
exponentiala (4) tinde la zero. Alegand pasul de simulare dupa
formula (3), chiar si exponentiala cea mai rapida
(corespunzatoare polului de modul maxim) este surprinsa in suficiente
(minim 10) puncte de simulare pana se anuleaza.
- lungimea intervalului de simulare [ t1, tn]
Se alege de lungime
suficient de mare, astfel incat sistemul sa atinga regimul permanent
de functionare (cand acesta exista). De regula, se prefera
ca regimul permanent sa fie reprezentat pentru aproximativ o treime din
intervalul de simulare (lungimea intervalului de simulare = 1.5* timpul de
raspuns al sistemului).
Daca lungimea
intervalului de simulare este prea mare, regimul tranzitoriu ajunge sa fie
descris pentru o portiune a intervalului de simulare care sa
reprezinte procentual prea putin din lungimea totala a intervalului
de simulare. In acest caz, pe reprezentarea grafica a marimii de
iesire performantele de regim tranzitoriu vor fi greu de urmarit.
Cu titlu orientativ se
poate folosi de formula:
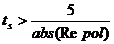 , (5)
, (5)
in care se considera
polul de parte reala minima in modul.
Aceasta lungime a intervalului
de simulare asigura, intuitiv, suficient timp pentru ca toate
exponentialele coresponzatoare polilor cu parte reala strict
negativa, continute de raspunsul sistemului, sa ajunga
la valori apropiate de zero.
In final, vectorul de timp
de simulare se retuseaza prin incercari repetate, plecand de la
cele enuntate anterior.
Se mareste
numarul punctelor de simulare, pana cand in reprezentarea grafica a
lui y(t) se obtine o curba neteda (fara puncte
de frangere) in domeniul t > 0. Se
ajusteaza lungimea intervalului de simulare pana cand regimul
tranzitoriu si permanent sunt reprezentate in proportii convenabile.
Lansati
programul demonstrativ esant.m
pentru a urmari pe un exemplu ce efecte poate avea alegerea
gresita a vectorului de timp t.
3.2 Functii pentru calcularea in Matlab a
raspunsului sistemului in domeniul timp
a)step
efect:
calculeaza raspunsul indicial al sistemului
argumente:
num, den, t
returneaza:
vectorul de iesire y=[y(0) y(p) .y(qp)]'
Sintaxa: y=step(num,den, t);
b)impulse
efect:
calculeaza raspunsul sistemului la o intrare de tip impuls Dirac
argumente:
num, den, t
returneaza:
vectorul de iesire y=[y(0) y(p) .y(qp)]'
Sintaxa: y=impulse(num,den, t);
c)lsim
efect:
calculeaza raspunsul sistemului la o un semnal de intrare oarecare u
argumente:
num, den, t, u
returneaza:
vectorul de iesire y=[y(0) y(p) .y(qp)]'
Sintaxa:
y=lsim(num,den,u, t);
se va folosi u=[u(0) u(p)u(qp)]'
Observatie: Cu ajutorul instructiunii plot (t, y) se poate reprezenta grafic iesirea sistemului.
4. Exercitii rezolvate in
Matlab
Exercitiul
1
Fie sistemul dinamic liniar, descris prin  . Reprezentati grafic raspunsul sistemului la
semnalul de intrare de tip treapta unitate, impuls Dirac si la un
semnal de intrare sinusoidal de forma u(t)=sin(0.8 t).
. Reprezentati grafic raspunsul sistemului la
semnalul de intrare de tip treapta unitate, impuls Dirac si la un
semnal de intrare sinusoidal de forma u(t)=sin(0.8 t).
Rezolvare:
num
=[1];den=[5 1]; %Descriere
sistem
T= 0:0.1:25; % Alegerea vectorului de timp T: polul
este 0.2 si
din formulele 5 si 3 % se poate
alege pas=0.1 si tn=25.
g =
impulse(num,den,T); %Determinarea
raspunsului la impuls
h =
step(num,den,T); %Determinarea raspunsului indicial
clf,subplot(211),plot(T,h,'r'),grid,
subplot(212),plot(T,g,'r'),grid;
% Graficele
pentru raspunsul la impuls si raspunsul indicial
figure;
u = sin(0.8*T); y = lsim(num,den,u,T);clf, plot(T,y,'r');
%
Determinarea raspunsului la semnalul u precizat:
Se
remarca faptul ca, in regimul permanent, acest sistem copie forma
semnalului de intrare (raspunsul la impuls tinde la zero, raspunsul
indicial tinde catre o constanta, raspunsul la o intrare sinusoidala
tinde catre o sinusoida). Acest lucru se intampla deoarece polii
sistemului (p = -0.2) sunt cu parte
reala strict negativa (p =
-0.2 < 0). Raspunsurile indicial si la impuls sunt aperiodice,
deoarece polul sistemului este real.
Exercitiul 2
Determinati
familia raspunsurilor indiciale pentru sistemul.
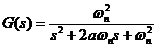 cu : ωn = 2.5 si
parametrul a= 0; 0.2; 0.4, 0.6, 0.8,1 ,
cu : ωn = 2.5 si
parametrul a= 0; 0.2; 0.4, 0.6, 0.8,1 ,
Reprezentati
grafic aceasta familie de raspunsuri:
Rezolvare
clear;t = 0:0.05:10;a = 0:0.2:1;
for i=1:6, den(i,:)=[1 2*a(i)*2.5
2.5^2]; end;
% fiecare linie din matricea den va
contine coeficientii din polinomul polilor
% pentru o valoare a.
for i=1:6,
H(:,i)=step([2.5^2],den(i,:),t);end;
% fiecare coloana din matricea H va contine raspunsul
indicial al sistemului
% pentru o valoare a.
clf, plot(t,H,'r'), grid;
%graficele sunt
trasate in acelasi sistem de axe, pentru toate valorile lui a.
Pentru a
= 0 raspunsul indicial este o sinusoida neamortizata (nu copie intrarea in
regim permanent), deoarece sistemul admite poli cu parte reala nula si
exponentialele acestora nu tind la zero. Pentru 0 < a < 1, raspunsul indicial este
oscilant amortizat (poli complecsi, conjugati). Pentru a >= 1, raspunsul indicial este
aperiodic - fara componente oscilante (poli reali).
5.
Probleme propuse
Problema 1
Calculati
analitic si verificati prin simulare, in Matlab, raspunsul
indicial, raspunsul la impuls si raspunsul la intrarea u(t)=sin2t, t ≥ 0, pentru sistemele
descrise prin functiile de transfer:
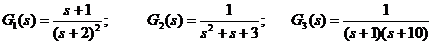 .
.
Atentie
la modalitatea de determinare a intervalului de simulare si a pasului de
distribuire a punctelor de simulare. Notati vectorii de timp
folositi.
Problema 2
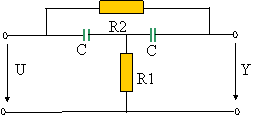
Fie
sistemul electric din figura 2.
Se
considera ca marime de intrare (cauza) tensiunea
electrica
notata
U si
ca marime
de iesire tensiunea electrica notata Y.
Precizati cum se va comporta sistemul sub actiunea unei intrari
constante u(t)=s(t), pentru cazul: C=1mF; R1=R2=1MW, stiind ca modelul
sistemului de tip functie de transfer este:
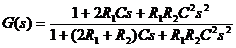
Cum
se va modifica raspunsul
sistemului atunci cand se dubleaza valoarea lui R1? Se modifica
valorile lui y(t) in
regim permanent? Dar pe durata regimului tranzitoriu? Folositi simularea
numerica.
Problema 3
Se
considera sistemul dinamic liniar descris prin functia de transfer  .
.
a) Determinati
raspunsul indicial (analitic si in Matlab); reprezentare
grafica.
b) Determinati si
reprezentati grafic raspunsul sistemului la o intrare de forma:
 .
.
Observati efectul
discontinuitatii lui u(t) asupra lui y(t).
c) Determinati si
reprezentati grafic raspunsul sistemului la o intrare de forma:
 .
.
Observati efectul
discontinuitatii lui u(t) asupra lui y(t).
Indicatie:
- raspunsul indicial al sistemului rezulta:
 ,
,
 .
.
- daca semnalul de
intrare este 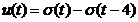 , atunci
, atunci  .
.
Raspunsul sistemului
la acest semnal de intrare este (vezi fig. 3):
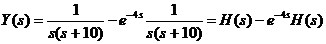
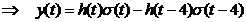 .
.

Fig. 3 Raspunsul ce trebuie obtinut la problema propusa
3.


 ,
,

 .
. .
.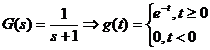 .
.
 .
.
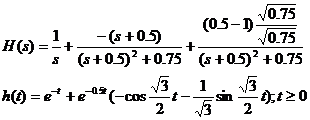
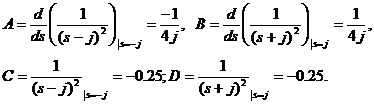 .
.