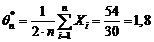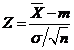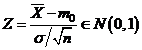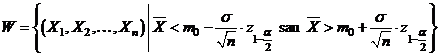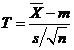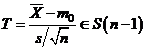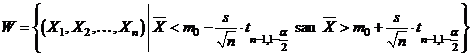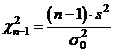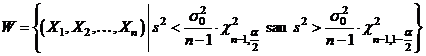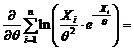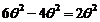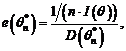Verificarea ipotezelor statistice

Verificarea ipotezelor statistice

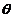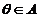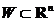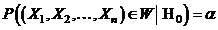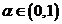Ipotezele pe care le facem se refera la valorile parametrilor repartitiei. Ipoteza pe care vrem sa o verificam se numeste ipoteza nula si o vom nota cu H₀. Ipoteza alternativa o vom nota cu H₁. Daca vrem sa verificam apartenenta parametrului la o submultime A din spatiul parametrului, deci H₀: , vom determina o regiune critica cu , unde nivelul sau pragul de semnificatie este apropiat de zero. Regula de verificare (testul) consta in acceptarea ipotezei nule (si respingerea alternativei) cand esantionul nu apartine regiunii critice si in acceptarea ipotezei alternative (si respingerea ipotezei nule) cand esantionul apartine regiunii critice. Nivelul de semnificatie 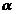se mai numeste si probabilitatea erorii de genul intai sau riscul de prima speta, adica probabilitatea de a respinge o ipoteza adevarata. Eroarea de genul al doilea este eroarea de a accepta o ipoteza falsa. Probabilitatea erorii de genul al doilea, numita si risc de speta a doua o vom nota cu 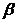, deci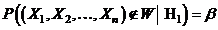

Probabilitatea de a respinge o ipoteza falsa se numeste puterea testului si o notam cu 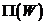, deci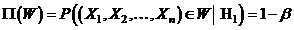

Verificarea ipotezei privind media repartitiei normale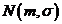

H₀: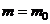

a). Daca 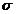este cunoscut se utilizeaza statistica 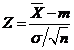si testul Z.

Testul Z bilateral: pentru alternativa  H₁: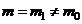

Daca H₀ este adevarata atunci 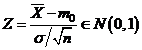si regiunea critica este formata in exteriorul intervalului de incredere cu nivelul de incredere 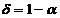, deci

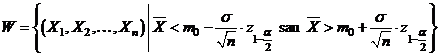
unde 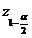este cuantila de ordin 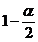a repartitiei normale standard.

Testul Z unilateral dreapta: pentru alternativa  H₁: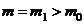

Regiunea critica este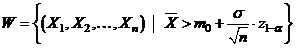

Testul Z unilateral stanga: pentru alternativa  H₁: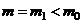

Regiunea critica este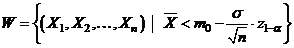

b). Daca 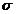este necunoscut se utilizeaza statistica 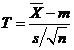si testul T.

Testul T bilateral: pentru alternativa  H₁: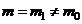

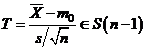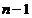Daca H₀ este adevarata atunci , repartitia Student cu grade de libertate, si regiunea critica este

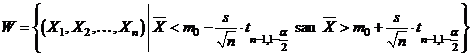
unde 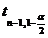este cuantila de ordin 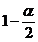a repartitiei Student cu 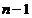grade de libertate.

Testul T unilateral dreapta: pentru alternativa  H₁: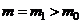

Regiunea critica este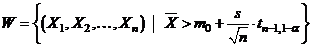

Testul T unilateral stanga: pentru alternativa  H₁:

Regiunea critica este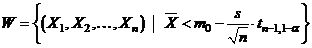

Verificarea ipotezei privind dispersia repartitiei normale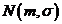

H₀: 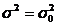fata de alternativa H₁: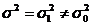

Folosim testul 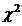(hi-patrat) bilateral. Cand H₀ este adevarata statistica 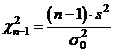are repartitia hi-patrat cu 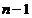grade de libertate. Regiunea critica este

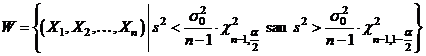
unde 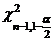si 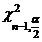sunt cuantilele de ordin 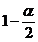, respectiv , ale repartitiei hi patrat cu 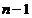grade de libertate.

Analog cazului mediei avem si test 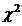unilateral dreapta si unilateral stanga.

Exercitiu Pe baza selectiei 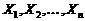sa se estimeze parametrul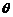 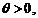din densitatea de repartitie: 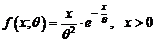si sa se analizeze estimatorul obtinut. Precizati estimatia in cazul selectiei de volum 15 si de valori: 4, 5, 5, 2, 3, 4, 5, 3, 4, 2, 3, 2, 5, 4, 3.

Rezolvare i) Folosind metoda momentelor avem:

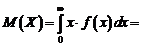
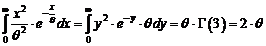, deci ecuatia 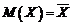ne da estimatorul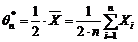

ii) Folosind metoda verosimilitatii maxime avem:

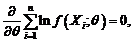
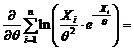
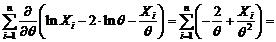
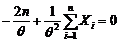, se obtine ecuatia 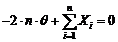, de unde rezulta estimatorul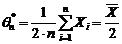  

Analiza estimatorului:

Avem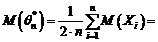

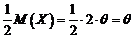
deci estimatorul este nedeplasat.

Cum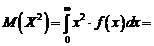

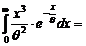
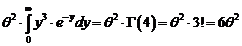obtinem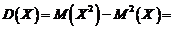 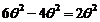si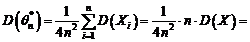

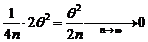
deci estimatorul este absolut corect.

Pentru a calcula eficienta estimatorului, 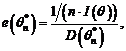procedam astfel: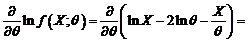

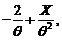
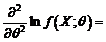
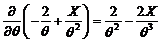
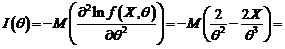
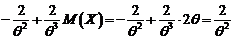
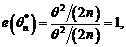asadar, estimatorul este eficient.

Pentru selectia data estimatia este