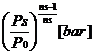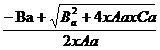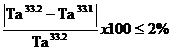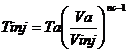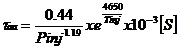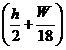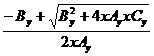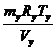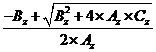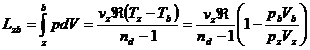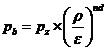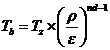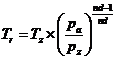CALCULUL
TERMIC AL MOTORULUI CU ARDERE INTERNA
Procesele ce se succed in motoarele cu ardere interna
reale sunt procese gazodinamice si termodinamice complexe, insotite
de schimburi rapide de caldura, masa, lucru mecanic cu mediul exterior si de asemenea de fenomene fizice si
chimice ce acompaniaza modificarile calitative si cantitative ale fluidului de lucru (formarea amestecului
carburant dintre aer si combustibil si arderea in timp a
acestuia). Conventional procesele care se desfasoara in
motoarele reale se impart in :
procese
de schimbare a gazelor (evacuarea si umplerea);
procesul
de comprimare;
procesul
de ardere;
procesul
de destindere;
1. Conditii de referinta
Pentru calculul motoarelor navale in conformitate si
cu recomandarile R.N.R in tara noastra se folosesc conditiile standard I.S.O. pentru zone tropicale:
temperatura aerului ambiant: 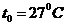
presiunea
mediului ambiant po=1 bar
umiditatea mediului ambiant h=60%
temperatura
apei la intrarea in racitorul aerului de supraalimentare ta=270C
Parametrii de calcul
Efectuarea
calculului termic al unui motor cu ardere prin comprimare presupune alegerea unor parametri initiali din datele statistice
furnizate de literatura de specialitate in domeniu si in conformitate
cu conditiile de exploatare ale motorului.
1. Date generale
referitoare la motor
Datele sunt rezultatul analizei efectuate in capitolul
anterior:
tipul motorului: motor diesel lent cu supraalimentare medie in r = 2
timpi
puterea motorului: Pen=336G kw (4500 BHP)
turatia : nn=200 rot/min
nr, cilindri: 1=6 L
Date
caracteristice proceselor si ciclului motor
coeficientul excesului de aer: a reprezinta
raportul dintre cantitatea molara reala de aer disponibila
pentru ardere si cantitatea molara de aer teoretica,
necesara arderii. Pentru cazul de fata a reprezinta
raportul dintre cantitatea molara reala de aer L care revine la 1 kg de combustibil si
cantitatea molara teoretica de aer necesara arderii acestuia Lmin:
 (1)
(1)
a
raportul de comprimare : ε este
raportul dintre volumul maxim Va si volumul minim Vc ocupat de fluidul
motor in cilindru:
 (2)
(2)
avansul la injectie :β unghiul
la care incepe injectia combustibilului inainte de punctul mort interior:
b = 4°RAC
coeficientul gazelor arse reziduale :y
este raportul dintre cantitatea molara de gaze arse reziduale vr
si cea de incarcatura proaspata introdusa in
cilindru L :
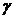 =
= 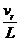 =
=
temperatura gazelor arse reziduale :Tr
depinde de tipul motorului, de raportul de comprimare si coeficientul
excesului de aer.
Tr = 775°K
presiunea aerului de supraalimentare :
ps este presiunea la iesirea din suflanta (sau compresor) a incarcaturii
proaspete.
ps = 298 KN/m2
presiunea in colectorul de evacuare :pev
valorile aproximative ale acestui parametru necesar efectuarii calculului
termic sunt cuprinse in plaja de valori:
pev=(0.450.7)ps
pev = 268.2 KN/m2
coeficientul de scadere a presiunii
la admisie :  a acest coeficient este definit ca fiind raportul dintre
presiunea la sfarsitul procesului de schimb de gaze pa si
presiunea aerului de supraalimentare
a acest coeficient este definit ca fiind raportul dintre
presiunea la sfarsitul procesului de schimb de gaze pa si
presiunea aerului de supraalimentare
x
coeficientii de utilizare a
caldurii : ξv si ξv sunt
definiti ca fiind raportul dintre cantitatea de caldura utilizata
pentru producerea lucrului mecanic exterior si cresterea energiei
interne a fluidului motor si cantitatea de caldura degajata
prin arderea combustibilului. Avem doi astfel de coeficienti, cate unul
asociat fiecarui tip de ardere izocora sau izobara:
xv =0.95
xp
coeficientul de alungire a bielei: l reprezinta
raportul dintre lungimea manivelei R si lungimea bielei L:
l
raportul cursa diametru : y care se alege
functie de tipul si destinatia motorului influentand dimensiunile
de gabarit ale motorului:
y
randamentul mecanic : ηm
este parametrul definit prin raportul dintre lucrul mecanic efectiv si cel
indicat:
hm
hm= = 0.80.9
= 0.80.9
coeficientul de plenitudine al diagramei
indicate : rf aproximeaza diagrama indicata reala care difera
de cea teoretica prin ariile pierdute la racordarile de la procesele
de schimb de gaze si ardere. Coeficientul de plenitudine este definit de
raportul dintre lucrul mecanic indicat real si cel obtinut cu ciclul:
ales pentru motorul analizat:
hm= = 0.80.9
= 0.80.9
hm
3. Analiza elementara a combustibilului
utilizat
Combustibilul
utilizat de motoarele navale este de tipul combustibil greu sau usor, o
clasificare a sortimentelor utilizate fiind realizata de standardele ISO8217:1987
sau BS MA 100:1989 sau CIMAC.
Compozitia procentuala a acestuia este reprezentata de:
carbon : c
hidrogen : h
oxigen
: o =0.01
sulf:S<0.01
apa:
apa <
cenusa:
cenusa = -
sedimente
: sedimente =
puterea
calorica specifica inferioara: Qi =42176
kj/hg
4. Gradul de supraalimentare a motorului
racirea intermediara aerului
de supraalimentare in racitor : ∆Trac
reprezinta caderea de temperatura pe racitorul aerului de
SA, ce utilizeaza drept agent de racire apa de mare. Pentru calcule
preliminare este estimata astfel:
∆Trac
=75o
exponentul politropic al
comprimarii in suflanta : ns comprimarea
aerului este considerata o transformare politropica al carei
exponent este:
ns=
caderea de presiune in racitorul
aerului de supraalimentare:Δps aferenta
pierderilor hidrodinamice:
∆Ps=0.3
5. Date referitore Ia traseul de admisie
incalzirea incarcaturii
proaspete in contact cu motorul: ΔT
∆T=80
3. Calcului procesului de admisie
In
functie de mijloacele care genereaza deplasarea coloanei de fluid
motor proaspat spre cilindrul
motorului se deosebesc doua procedee de baza in
desfasurarea procesului de admisie
procesul de
admisie normala, sau umplere
normala, la care fluidul motor proaspat patrunde in cilindru datorita volumului eliberat si
depresiunii create in acesta de deplasarea pistonului inspre p.m.e.
(situatie intalnita la motorul in patru timpi)
procesul de admisie
fortata, sau umplere fortata,
la care fluidul motor proaspat patrunde in cilindru datorita efectului combinat al comprimarii
prealabile a incarcaturii si a deplasarii pistonului la o presiune
superioara celei atmosferice; in cazul in care pentru comprimarea
fluidului motor se utilizeaza o
suflanta (compresor) acest procedeu de umplere se mai numeste si
sapraalimentare; studiul
supraalimentarii motoarelor navale se va face intr-un volum ulterior.
Motoarele in patru timpi pot fi atat cu admisie normala
(aerul patrunde in sistemul de admisie in conditiile de stare ale mediului ambiant: presiunea po si
temperatura T0, cat
si cu admisie fortata, cand se urmareste cresterea puterii motorului (incarcatura
proaspata patrunde in sistemul de admisie cu presiunea ps si temperatura Ts
de la iesirea din agregatul de precomprimare). Motoarele in doi timpi
pot fi numai cu admisie fortata.
Marea majoritate a motoarelor
moderne cu aprindere prin comprimare sunt supraalimentate, iar cele
navale aproape in totalitate.
3.1. Presiunea de admisie
Pa=eaPs bar
pa
=274.16 KN/m2
3. Temperatura de admisie(calcul simplificat)
Ta= [K]
[K]
unde:
temperatura aerului la iesirea din suflanta:
Ts=T0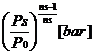
Ts= 385.9719795 K
temperatura dupa racitorul aerului de supraalimentare
Ts=Ts-ATrac.[K]
Ta=310.9719795 K
temperatura aerului la intrarea in cilindru :
Ts=T's+AT{K]
Ts=318.9719795
K
3.3. Temperatura de admisie(calcul detaliat)
Cantitatea de oxigen necesara arderii complete a 1 kg. de combustibil:
Omin
= 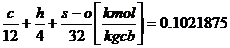
Cantitatea de aer necesara arderii complete a 1 kg. de combustibil
Lmin
= 
Produsele
arderii:
V 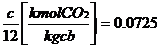
VSO2 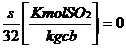
VO2 = 0.21 x (a-1) x Lmin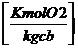 (23)
(23)
Vn2= 0.79 x a x Lmin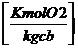 (24)
(24)
Cantitatea totala de produse ale arderii este:
Vpa= j=CO2H2O2SO2O2N2 Vpa=0.97971964 (25)
j=CO2H2O2SO2O2N2 Vpa=0.97971964 (25)
Participatiile volumice ale produselor arderii
Yj = 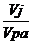 Verificare:
Verificare: 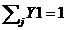
Cantitatea de gaze arse reziduale.
Mr = Vgar = Yr x L  (27)
(27)
Compozitia gazelor arse reziduale :
Vgarj = Yj x Vgar
(28)
Verificare:

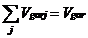 (29)
(29)
- masa amestecului la sfarsitul admisiei:
Ma=LxMaer+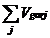 xMj
xMj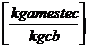
Ma = 28.46532074
Masele molare ale speciilor
prezente in amestecul format la finele admisiei sunt prezentate in tabelul 1:
Tabelul 1
|
Specia j
|
Aer
|
CO2
|
H2O
|
SO2
|
O2
|
N2
|
|
Mj
|
|
|
|
|
|
|
- constanta amestecului la sfarsitul
admisiei:
Ra= Ax 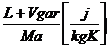 Ra=288.2317878 (30)
Ra=288.2317878 (30)
S-a notat cu A  constanta
universala a gazelor.
constanta
universala a gazelor.
- calculul
temperaturii de admisie :
Din ecuatia de bilant
energetic rezulta:
la=laer+lgaz (31)
in care:
laer = L x (Aaaer +
Bbaer x T"s) x T"s (32)
lgaz= 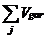 x (Aaj + Bbj x Tr)
x Tr (33)
x (Aaj + Bbj x Tr)
x Tr (33)
In scrierea expresiilor entalpiilor
din ecuatia de bilant s-a tinut cont de variatia
liniara a caldurii specifice izobare cu temperatura (vezi
coeficientii Aaj si Bbj
).Tinand cont de aceasta si de ecuatia de bilant
relatia poate fi rescrisa sub forma unei ecuatii de gradul doi
ce are ca necunoscuta doar temperatura la sfarsitul admisiei:
Aa x T2a + BaTa
- Ca = 0 (34)
ai carei
coeficienti sunt:
Aa = L x Baaer +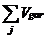 x Aaj(35)
x Aaj(35)
Aa
= 0.002317528
Ba = L x Aaaer + 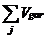 x Aaj (36)
x Aaj (36)
Ba
= 19.439657475
Ca
= L x (Aaaer + Bbaer x T"s)
x T"s + 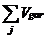 x (Aaj + Bbj
x Tr) x Tr
x (Aaj + Bbj
x Tr) x Tr
Ca = 6878.081896 (37)
Solutia
ecuatiei este temperatura de admisie:
Ta =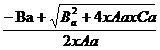 (38)
(38)
Ta =
338.93952740K
Valorile coeficientilor
sunt dati in tabelul 2:
Tab. 2
|
Specia
|
Aer
|
CO2
|
H2O
|
SO2
|
O2
|
N2
|
|
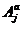
|
19.67
|
27.62
|
23.01
|
30.97
|
19.25
|
19.67
|
|
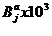
|
51
|
11.72
|
5.44
|
11.72
|
4.6
|
51
|
calculul erorii in estimarea temperaturii de admisie:
∆Ta =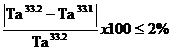 (39)
(39)
∆Ta =
0.721523196
volumul amestecului la sfarsitul admisiei:
Va= (40)
(40)
Va=
10.143190418m3
coeficientul de umplere :
hv 
ηv
=0.880503109
S-a notat cu Pg presiunea aerului la iesirea din
racitorul aerului de supraalimentare:
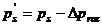 (42)
(42)
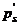
Tabelul cu
valorile calculate se gaseste la sfarsitul capitolului intr-un
tabel centralizator alaturi de
variabilele de intrare se alege conform recomandarilor de la inceputul
capitolului.
Tot la sfarsitul capitolului se
gasesc si graficele presiune functie de volum si presiune
functie de unghiul de manivela.
4. Calculul procesului de comprimare
In conditiile ciclului teoretic, comprimarea este considerata
drept un proces adiabatic, care se desfasoara pe intreaga
durata a cursei pistonului (p.m.e., p.m.i), adica corespunde unei
variatii de volum egala cu volumul util al cilindrului.
In realitate, la motorul cu ardere interna,
comprimarea se desfasoara in conditiile unei variatii continue a temperaturii amestecului proaspat si
a existentei unui schimb de caldura intre amestecul carburant,
peretii cilindrului si ai camerei de ardere, precum si a
scaparii unei parti din amestecul carburant prin
neetanseitati.
Comprimarea incarcaturii proaspete in cilindrul
motorului reprezinta un proces complex care depinde de o
serie de factori si anume:
schimbul de
caldura variabil dintre incarcatura si
pereti, care variaza atat in marime cat si ca sens;
micsorarea
continua a suprafetei de racire pe masura apropierii
pistonului de p.m.i.
scaparile
parpiale ale incarcaturii prin neetanseitapile segmentilor
de piston;
injectarea si
evaporarea unei parti combustibilului in cilindru inainte de terminarea
procesului de compresiune.
Datorita
acestora procesul comprimarii se desfasoara politropic.
Exponentul politropic nc al compresiunii
procesului real este valabil de-a lungul intregii linii de compresiune.
Pentru
trasarea politropei de comprimare trebuie sa se stabileasca valoarea
exponentului de comprimare nc,
care exprima volumul specific, din ecuata curbei reprezentative a
procesului.
pVnc =const.
4.1. Determinarea exponentului politropic mediu ele
comprimare
Parametrii gazelor din cilindrul motorului la
sfarstul cursei de comprimare se determina, folosind
exponentul adiabatic aparent, care tine seama de variatia reala
a caldurii specifice cu temperatura,
schimbul de caldura intre incarcatura proaspata
si peretii cilindrului si pierderile de substanta
fiind egale cu zero.
Determinarea valorii exponentului adiabatei aparente kc
este deosebit de importanta pentru aprecierea corecta a
exponentului politropei nc ce aproximeaza procesul de comprimare,
tinand seama de particularitatile
acestui proces la motorul proiectat (se exclud astfel posibilitatile
unor erori mari la alegerea lui nc, se apreciaza ca: nc
= 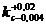
Ecuatia bilantului energetic ce
aproximeaza evolutia procesului de comprimare este:

in care s-a
tinut cont de considerarea comprimarii ca o evolutie adiabatica.
Pentru lucrul mecanic de comprimare avem:
 (45)
(45)
in care va este numarul de kmoli de amestec in
starea a, L numarul de kmoli de aer admis in cilindru pentru arderea unui kg de combustibil, yr coeficientul
gazelor arse reziduale, iar 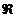 este constanta reala a
gazelor.
este constanta reala a
gazelor.
Variatia energiei interne va fi:
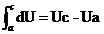 ,
,
care se poate scrie sub forma:
Ua(c)
= L(Aaer + Baer Ta(c))Ta(c)
+ 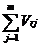 (Aj+BjTa(c))Ta(c) (47)
(Aj+BjTa(c))Ta(c) (47)
In
relatia anterioara, cu A(B)aer si A(B)j s-au notat
coeficientii polinomiali ai variatiei specifice cu temperatura (variatii liniare), dati in
literatura de specialitatevrj numarul kmoli de gaze
reziduale de specia j.
Prin prelucrari succesive, ecuatia (44) conduce
la relatia urmatoare, ce constituie o ecuatia ascendentala
in necunoscuta nc.
nc-1=
unde coeficientii Ac si Bc
au forma si sunt identici cu cei din Tab. 3.2
Ac=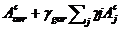 (49)
(49)
Ac=20.48686556
Bc=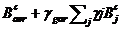
Bc = 0.002653146
Ecuatia (48) se poate rezolva, de exemplu, prin
metoda iteratiei: se admite in mod arbitrar nc=l.35-1.36 si se
calculeaza prima data membrul drept al relatiei,
obtinandu-se o noua valoare aproximativa a lui nc, care
se introduce in membrul drept al ecuatiei, procedandu-se la fel ca si
inainte pana se obtine o valoare a
sa cu o aproximatie satisfacatoare sau grafic.
De asemenea sunt o serie de programe de calcul care
rezolva ecuatii folosind diversi algoritmi de calcul. Programul
folosit a utilizat un algoritm de calcul bazat pe metoda coardei cu o precizie
de 0.0001 care pentru calculele curente este
suficient, marimile posibil de determinat experimental ne avand o
precizie mai mare de 0.01.
Algoritmul de calcul propus este unul simplificat
deoarece nu ia in considerare si schimbul de caldura dintre fluidul de lucru si peretii cilindrului.
Programul de calcul propus in capitolul urmator va tine
cont si de schimbul de caldura.
4. Parametrii amestecului la sfarsitul
comprimarii
Pc =
Pasn°[bar] (51)
pc=11988.838463
Vc=
Vc
= 0.633949401
(53)
Tc=Ta 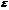 nc-1[k]
nc-1[k]
Tc = 926.3503161
4.3. Verificarea incadrarii in valorile uzuale
pc
=50...100 bar
TC=700-950K
5. Calculul procesului de ardere
Combustibilul lichid este injectat, cu avans
fata de p.m..i, prin orificiile calibrate ale pulverizatorului montat la o extremitate a injectorului, la o presiune mare
si o viteza relativa (fata de aer) ridicata, sub
forma de jet. Datorita acestei viteze mari, jetul se
dezintegreaza in picaturi de combustibil, care, impreuna cu
miscarile aerului in cilindru, conduc la o dispersie a jetului, la amplificarea
foarte mare a suprafetei de contact faza lichida faza
gazoasa si deci a vitezei de vaporizare, simultan cu dirijarea
combustibilului. Calculul efectuat in continuare schematizeaza arderea
reala folosind o transformare izocora si una izobara
neglijand schimbul de caldura cu mediul extern si ne tinand
cont de fenomenele gazodinamice ce se desfasoara in cilindru.
Un calcul mult mai elaborat se va dezvolta in capitolul
urmator cand arderea va fi abordata luand in considerare si
celelalte fenomene care intervin: vaporizarea fenomenele de amestecare si difuzie dar tot la nivel global o abordare mai
pretentioasa fiind foarte greu de realizat datorita complexitatii
fenomenelor.
5.1. Calculul
parametrilor la inceputul injectiei
volumul fluidului
motor in momentul declansarii injectiei:
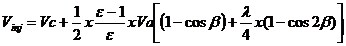
Vinj= 0.648387692
unde b este unghiul de avans la
injectie.
presiunea
fluidului motor in momentul declansarii injectiei:
Pinj=Pa [bar] (55)
[bar] (55)
pinj=
11626.535882
temperatura
fluidului motor in momentul declansarii injectiei
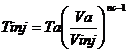 [K] (56)
[K] (56)
Tinj=918.8162088
intarzierea la
autoaprindere :
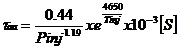

 (58)
(58)
unghiul perioadei
de intarziere la autoaprindere


unghiul
corespunzator duratei totale a injectiei
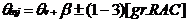 (60)
(60)
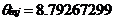
5. Arderea !a volum constant
cantitatea de
combustibil arsa la volum constant
mv=1x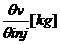 (61)
(61)
mv=
cantitatile
de gaze la sfarsitul arderii izocore
nYCO2 = mvx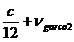 = mv x nCO2
= mv x nCO2 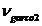
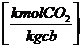 (62)
(62)
nYCO2
nYH2O =
mvx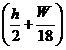
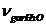 = mv x nH2O +
= mv x nH2O +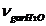
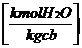 (63)
(63)
nYH2O (64)
nYSO2 = mvx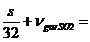 mvx nSO2+
mvx nSO2+
 (65)
(65)
nYSO2
nYO2 = 0.21x(a-mv)x
Lmin+ 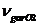
 (66)
(66)
nYO2
nYN2 = 0..79xa Lmin+
 (67)
(67)
nYN2
masa fluidului motor la
sfarsitul arderii izocore:
mY = 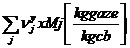 (68)
(68)
mY
constanta amestecului la sfarsitul arderii
izocore:
Ry=(Ax )x
)x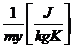 (69)
(69)
Ry = 287.8029091
calculul temperaturii amestecului la
sfarsitul arderii izocore :
Ecuatia
primului principiu pentru arderea izocora are forma:
Uy=Uc+xvxmvxQi
unde:
Uc=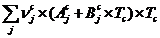 (71)
(71)
Uy=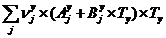 (72)
(72)
Prin prelucrari succesive se obtine ecuatia de gradul doi:
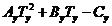 (73)
(73)
ai carui coeficienti sunt:
Ay=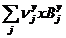 (74)
(74)
Ay= 0.001787632
By=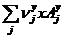 (75)
(75)
By= 209073609
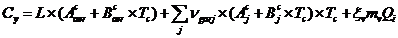 (76)
(76)
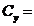 33977.24728
33977.24728
Temperatura in starea y este:
Ty=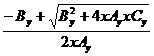
Ty= 1383.243224
Coeficientii  sunt estimate cu valorile prezentate
in tabelul 3:
sunt estimate cu valorile prezentate
in tabelul 3:
Tab. 3
|
Specia
|
CO2
|
H2O
|
SO2
|
O2
|
N2
|
|
Ajy
|
|
|
|
|
|
|
Bjy
|
|
|
|
|
|
volumul la sfarsitul arderii
izocore :
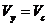
 = 0.633949401
= 0.633949401
presiunea fluidului motor la
sfarsitul arderii izobare:
py=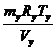
Py= 18089.11318
5.3. Arderea la presiune constanta
cantitatea de combustibil arsa la
presiune constanta
mp
= 1- mv [kg] (79)
mp = 0.659640135
cantitatile de gaze la
sfarsitul arderii izobare
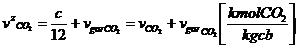 (80)
(80)
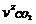


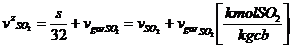 (82)
(82)
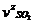
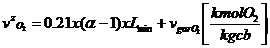 (83)
(83)
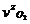
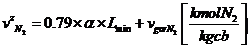 (84)
(84)
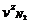
masa fluidului motor la sfarsitul
arderii izobare
mz=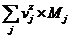
 (85)
(85)
mz=29.46532074
constanta amestecului la sfarsitul
arderii izobare
Rz=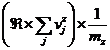
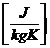 (86)
(86)
Rz=287.0017951
calculul temperaturii amestecului la
sfarsitul arderii izobare :
Ecuatia primului principiu pentru arderea
izobara are forma:
Iz =
Iy + xp x mp
x Qi
unde:
Ly
=  (88)
(88)
Lz = 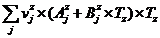
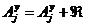
Prin
prelucrari succesive se obtine ecuatia de gradul doi:
AzT2z+BzTz-Cz=0
ai carui coeficienti sunt:
Az= 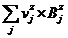 (92)
(92)
Az = 0.002033956
Bz= B7
= (93)
Cz = 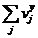 (
( + B
+ B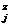 x Ty) x Ty + ξp
x mp x Qy (94)
x Ty) x Ty + ξp
x mp x Qy (94)
Cz = 69390.39333
Temperatura in starea z este:
Tz=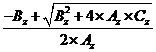
Tz= 194032906
Coeficientii Ajz si Bjz
sunt estimati cu valorile prezentate in tabelul 4:
Tab. 4
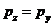
pz=
18089.11318
volumul fluidului motor la
sfarsitul arderii
 (96)
(96)
Vz
5.4.
Verificarea incadrarii in valorile uzuale
pv <140bar
Tz = 15002400K
T7 = 19403
6. Calculul procesului de destindere
Ca si in
cazul procesului de comprimare, destinderea ar putea fi considerata,
teoretic, ca un proces adiabatic. in
realitate, datorita faptului ca temperatura gazelor este permanent
superioara celeia peretilor cilindrului, procesul de destindere se
desfasoara in conditiile unei cedari permanenete de caldura
catre acestia.
La inceputul destinderii, diferenta
mentionata de temperatura este mai mare, suprafata de
schimb de caldura fiind insa mai redusa; odata cu
deplasarea pistonului spre p.m.e., se ajunge la cresterea suprafetei laterale de schimb de caldura
si la reducerea temperaturii gazelor.
Datorita fenomenului anterior, evolutia de
destindere, ca si cea de comprimare se desfasoara
politropic. Exponentul politropic al destinderii, nd, este variabil pe intreaga
durata a procesului, marimea sa depinzand de
urmatorii factori:
arderea posterioara, prin care se realizeaza un surplus de caldura (Qpost), ce
produce cresterea temperaturii gazelor, exponentul politropic fiind
inferior celui adiabatic: nd<kd; valori experimentale ale exponentului politropic mediu se situeaza in
gama 1.1-1.2, pentru prima etapa a procesului de destindere;
transferul de caldura dinspre gazele de ardere spre peretii cilindrului, ceea ce produce o
crestere a exponentului politropic in
continuarea destinderii, spre valorile 1.4-1.5, superioare celui adiabatic, nd>kd;
Exponentul politropic mediu se poate determina prin diferentierea
relatiei:

nd= 1.2892170103136
pVnd =const.
6.1. Determinarea exponentului politropic mediu de
destindere
Determinarea parametrilor fluidului motor la finele
procesului de destindere se determina, pentru cazul simplificat, util calcului ciclului termic al motorului, prin
adoptarea unor ipoteze simplificatoare, cum ar fi:
arderea se sfarseste in punctul z, deci nu avem postardere; de
asemenea, in timpul destinderii nu intervine schimb de
caldura intre gazele de ardere si peretii
cilindrului si nu exista scapari de gaze prin
neetanseitati.
Ecuatia de bilant energetic se scrie, in cazul destinderii,
pornind de la forma diferentiala:
pdV+dU = Q
unde lucrul mecanic efectuat in exteriorul sistemului termodinamic se
exprima prin relatia:
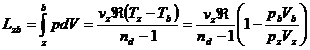 (100)
(100)
unde cu nd
s-a notat exponentul politropic aparent de destindere, iar variatia
energiei interne prin:
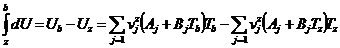 (101)
(101)
In relatiile anterioare, cu vz s-a notat numarul de kmoli din
starea z, iar Aj si Bj sunt coeficientii
polinomiali ai caldurilor specifice, limitate la functii liniare cu
temperatura. Introducerea expresiilor (101) si (100) in (99)
conduce la ecuatia transcendenta:

unde coeficientii Ab si Bb sunt:

Ab = 293088739
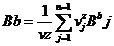
Bb = 0.001999658
cu ajutorul
carora exponentul politropic aparent nd se poate determina prin
calcul numeric metoda iteratiei sau
prin metoda grafica. Valori de start pentru aceasta marime:
1.25-1.30.
6. Volumul la sfarsitul destinderii

Vb =10.143190418
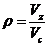 (105)
(105)
p= 1.43212359
6.3. Presiunea la sfarsitul destinderii
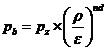
pb = 805.6344406
6.4. Temperatura la sfarsitul destinderii

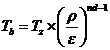
Tb =
966.310762
6.5. Verificarea incadrarii in valorile uzuale
pb = ..8 bar
Tb =900 1300 K
6.6. Verificarea temperaturii gazelor arse reziduale
Temperatura este estimata cu relatia:
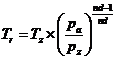
Tr = 764.6532981379
Calculul parametrilor din starile caracteristice ale
ciclului este considerat corect atunci cand conditia
urmatoare este verificata.
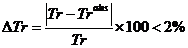
ΔTr = 0.35
7. Ciclul motor care lucreaza cu 1 kg de
combustibil
7.1. Tabel recapitulativ al parametrilor de stare
In
continuare vom prezenta parametrii de intrare alesi pentru motorul
prezentat AT 25 si tabelele cu valorile
ce vor fi folosite si in capitolele urmatoare pentru efectuarea de
comparatii intre diversele metode de calcul a ciclului motor.
Parametrii de alesi initiali se gasesc in
tabelul 5
Tab. 5
|
Marime
|
Simbol
|
Unitate
masura
|
Valoare
aleasa
|
|
Coeficientul de exces de aer
|
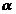
|
|
|
|
Raportul de comprimare
|
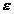
|
|
|
|
Coeficientul gazelor arse reziduale
|
 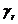
|
|
|
|
Temperatura gazelor arse reziduale
|
Tr
|
°K
|
|
|
Presiunea
aerului de supraalimentare
|
Ps
|
bar
|
|
|
Presiunea in
colectorul de evacuare
|
Pev
|
bar
|
|
|
Coef. de
scadere a pres. de admisie
|
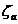
|
|
|
|
Unghiul de avans
la injectie
|
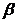
|
°RAC
|
|
|
Coef. de utilizare a caldurii la
v=ct
|
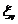
|
|
|
|
Coef. de utilizare a caldurii la
p=ct
|

|
|
|
|
Incalzirea
incarcaturii proaspete
|
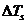
|
grd
|
|
|
Racirea intermediara a aerului de SA
|
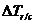
|
grd
|
|
|
Coef. de
alungire a bielei
|
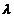
|
|
|
|
Randamentul
mecanic
|
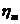
|
|
|
|
Coef. de
rotunjire al diagr. indicate
|
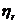
|
|
|
Parametrii de stare ai motorului se gasesc in
tabelul 6.Acestia difera de cei ce vor fi calculati in capitol anterior deoarece programul de calcul a fost
imbunatatit si s-a completat si cu date ce iau
in considerare fenomenele gazodinamice de la procesul de admisie.
Tab .6
|
Starea
|
p[bar]
|
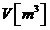
|
T[K]
|
|
A
|
|
|
|
|
C
|
|
|
|
|
Y
|
|
|
|
|
Z
|
|
|
|
|
B
|
|
|
|
7. Lucrul mecanic indicat (metoda analitica)
Acesta se estimeaza cu relatia:
 (110)
(110)
Li = 20194.97
8. Parametrii indicati ai motorului
8.1. Presinea medie indicata
Pi =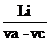 [bar] (111)
[bar] (111)
Pi = 21372
Verificare: pi=10 . 25 bar
8. Randamentul indicat

 = 0.47
= 0.47
Verificare:  = 0.38 0.47.
= 0.38 0.47.
8.3. Consumul specific indicat de combustibil
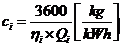
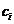 = 0.18
= 0.18
Verificare: Ci=0.160 0.225 kg/kwh
9. Parametrii efectivi ai motorului
9.1. Presiunea medie efectiva
Pe= ePi[bar]
ePi[bar]
Pe= 19.11
Valori curente: pe=7.5 20 bar
9. Randamentul efectiv
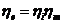
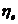 =0.4
=0.4
Valori curente: 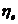 =0.30
=0.30
9.3. Consumul specific efectiv de combustibil

 (116)
(116)
ce = 0.129 kg/kwh.
Valori curente: ce=0.215 0.285 kg/kwh.
10. Parametrii motorului real
10.1. Puterea indicata ceruta
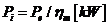
Pi = 3733.33
10. Lucrul mecanic pe cilindru necesar

Li cerut =
186.67
10.3. Coeficientul de similitudine
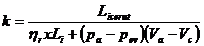
k = 0.01
10.4. Volumele in punctele caracteristice ale
ciclului real
V'a=kVa
V'a= 0.09
V'b= kVb
V'b=0.09
V'c=kVc
V'c= 0.01
V'y'=kVy
V'y'
V'z kVz
V'z =0.01
10.5. Tabel recapitulativ al parametrilor de stare
reali
Parametrii de stare calculati sunt centralizati in tabelul 7:
Tab .7
|
Starea
|
p [bar]
|
V[m3]
|
T[K]
|
|
a
|
|
|
|
|
C
|
|
|
|
|
Y
|
|
|
|
|
Z
|
|
|
|
|
B
|
|
|
|
10.6. Lucrul mecanic dezvoltat de motor
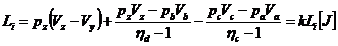
Li =188.55
11. Dimensionarea motorului
11.1. Cilindreea motorului (unitara)
Vs=V'a-V'c[m3]
Vs=
11. Diametrul pistonului (alezajul)

D'=
11.3. Calculul erorii in determinarea diametrului
pistonului
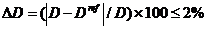
unde Dref este alezajul motorului de referinta
ΔD= 1.27529733714285
11.4. Cursa pistonului
S=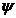 D [m]
D [m]
S=1.05
11.5. Raza manivelei
R=S/2 [m]
R = 0.53
L=R/λ [m]
l = 13
11.6. Lungimea motorului
Lm=cixDxi[m]
unde ci=2/9.
Lm=5.25
11.7. Latimea motorului
B=cbxS[m]
B= 5.65
unde Cb=4.34/6.3.
11.8.Inaltimea motorului
H=chxS[m]
unde Ch=6 8.5.
H = 7.35