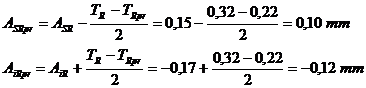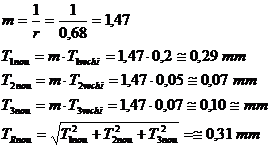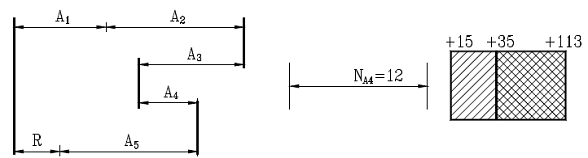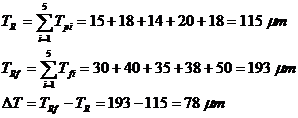Lanturi de dimensiuni
1 Consideratii generale
In constructia
de masini si aparate dimensiunile
liniare si unghiulare determina
marimea si forma suprafetelor precum si pozitia
a doua sau mai multe suprafete ale unei piese si de asemenea pozitiile pieselor
in cadrul unui subansamblu sau
ansamblu. Ca urmare, intre diferitele dimensiuni ale unei piese sau ansamblu de
piese exista anumite legaturi, directe si indirecte, cu caracter functional si
tehnologic.
Prin lant
de dimensiuni se intelege totalitatea
dimensiunilor liniare, unghiulare dispuse intr-o anumita succesiune, determinata de considerente functionale si
tehnologice, intr-un contur inchis
si care determina pozitia unor
suprafete ale unei piese sau piese intr-un subansamblu sau ansamblu.
Un
lant de dimensiuni se compune din
elemente primare si elementul de inchidere. Elementele primare sunt cele care se realizeaza in
procesul tehnologic si care trebuie sa fie realizate
la dimensiunile si abaterile prescrise in desenul de executie. Dimensiunea elementului de inchidere rezulta din dimensiunile elementelor primare ale lantului atat la
prelucrarea pieselor, cat si la asamblarea acestora.
In
desenele de executie, dimensiunea elementului de inchidere nu se inscrie, deoarece rezulta din conditia
dimensionala a lantului.
Un lant de dimensiuni poate avea trei elemente: doua elemente primare si
elementul de inchidere (sau
rezultanta). Ajustajele asamblarilor cilindrice pot fi considerate
lanturi cu trei dimensiuni: diametrul alezajului si arborelui
fiind dimensiuni primare, iar jocul sau strangerea dimensiunea rezultanta
(de inchidere).
In
Fig.1 se prezinta exemple de lanturi
de dimensiuni liniare si unghiulare, cu notatii conventionale (Fig.1 a si d) si cu valori
numerice (Fig.1 b si c), unde
dimensiunea de inchidere este j
(Fig.1a), R (Fig.1 b,c) si RA (Fig.1d).
|
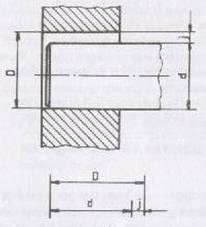
a) d si D sunt elemente primare iar j este elemental
de inchidere.
|
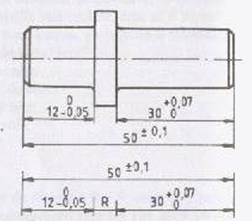
b)
|
|
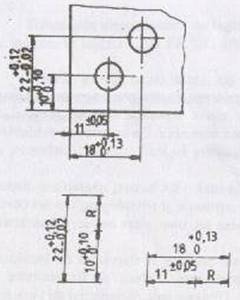
c)
|
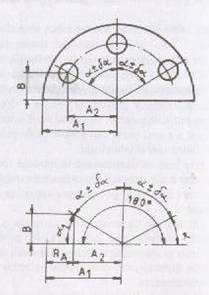
d)
|
Fig.1 Exemple de lanturi de
dimensiuni.
Clasificarea
lanturilor de dimensiuni se poate
face dupa urmatoarele criterii:
dupa destinatie:
lanturi
de dimensiuni functionale;
lanturi
de dimensiuni tehnologice.
In
cotarea functionala
(intocmita de proiectantul constructiv) dimensiunile sunt asezate cel mai des in serie astfel incat sa corespunda
rolului functional al piesei, fara a se tine seama de complicatiile tehnologice legate de existenta bazelor de cotare diferite pentru fiecare
dimensiune. In cotarea tehnologica, prin care se urmareste realizarea cat mai usoara si ieftina a
dimensiunilor se aplica principiul numarului minim de baze de cotare si se incearca
ca bazele de cotare tehnologica sa coincida cu cele functionale.
dupa apartenenta:
lanturi
de dimensiuni ale pieselor luate individual;
lanturi de dimensiuni de asamblare
dupa tipul dimensiunilor:
lanturi
de dimensiuni liniare: - paralele (Fig.2a);
- neparalele (Fig.2b);
lanturi
de dimensiuni unghiulare: - cu varf comun;
- fara varf comun;
lanturi
de dimensiuni mixte (Fig.1d);
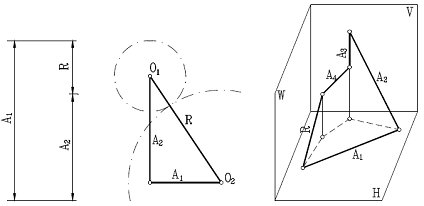
a) b) c)
Fig.2 Lanturi de dimensiuni: a)
liniare paralele; b) plane; c) spatiale.
dupa pozitia in plan sau spatiu a
dimensiunilor:
lanturi
de dimensiuni plane: - liniare, neparalele (Fig.2b) ;
- unghiulare;
- mixte (Fig.1d);
- lanturi de dimensiuni spatiale (Fig.2c).

Fig.3 Legarea lanturilor de
dimensiuni: a) paralela; b) in serie; c) mixta.
dupa legaturile existente intre diferitele elemente ale lanturilor de
dimensiuni:
simple (Fig.9.1 a, b, c);
complexe: - serie (Fig.3b);
- paralele (Fig.3a);
- mixte (Fig.3c);
dupa baza
de cotare:
cu
baza de cotare unica pentru toate elementele primare;
cu
baze de cotare diferite, pentru fiecare element primar;
cu
baza de cotare mixta;
dupa locul de unde rezulta:
lanturi
de dimensiuni: - la proiectare;
- la
prelucrare;
- la montaj;
- la masurare;
Din analiza oricarui lant
de dimensiuni reiese legatura dintre
elementele componente si
elementul de inchidere. Din exemplul
prezentat in Fig.4 se observa ca pentru a se realiza inchiderea
lantului trebuie sa existe egalitatea:
N1+ N2 = N3 + N4
+ N5 + R
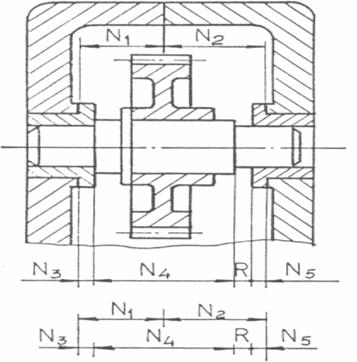
Fig.4 Ansamblu redactor.
In functie de
influenta pe care o are fiecare dimensiune a elementelor primare asupra dimensiunii elementului de inchidere, elementele primare se clasifica in:
elemente
maritoare (de marire sau pozitive)
- cele care prin cresterea lor (considerand constante celelalte elemente primare)
determina cresterea dimensiunii
elementului de inchidere (ex. N1
si N2 din Fig.4);
elemente
reducatoare (de micsorare sau negative) - cele care prin cresterea lor (considerand constante
celelalte elemente primare) determina scaderea,
micsorarea dimensiunii elementului de inchidere
(ex. N3, N4 si N5 din Fig.4).
2 Metode de rezolvare a lanturilor de dimensiuni
In teoria
si practica lanturilor de
dimensiuni se intalnesc doua probleme
principale:
problema directa, care apare cand se
cunosc dimensiunile nominale, tolerantele si abaterile limita ale dimensiunilor primare si se cere sa se
determine dimensiunea, toleranta si abaterile limita ale dimensiunii elementului
de inchidere (problema de
verificare);
problema inversa (sau de proiectare), care apare cand se cunosc dimensiunile nominale, toleranta
si abaterile limita ale elementului de inchidere
si valorile nominale ale dimensiunilor primare si se cere sa se determine tolerantele si abaterile limita ale acestora.
Metodele de rezolvare
a lanturilor de dimensiuni sunt variate si duc la rezultate diferite. Alegerea metodei de rezolvare se face
in baza urmatoarelor ipoteze:
ipoteza
interschimbabilitatii totale;
ipoteza
interschimbabilitatii partiale.
Pentru fiecare din aceste ipoteze exista
mai multe metode de rezolvare si la prezentarea lor se vor enumera avantajele
si dezavantajele.
3 Rezolvarea problemei directe a lanturilor de dimensiuni liniare paralele
Aceasta problema se poate rezolva in ipoteza
interschimbabilitatii totale prin urmatoarele metode:
metoda
de maxim si minim;
metoda
algebrica;
metoda
probabilistica.
3.1 Metoda de maxim si minim
Aceasta metoda este prezentata pe un caz
concret, spre exemplu lantul de dimensiuni din Fig.5, unde notam elementele primare astfel: 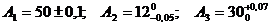 .
.
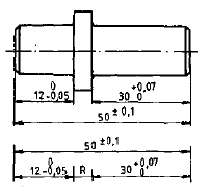
Fig.5
Dimensiunea
nominala a elementului de inchidere notata NR din conditia dimensionala a lantului este:
NR = N1 - (N2 + N3) (1)
unde: N1,
N2, N3 sunt dimensiunile nominale ale elementelor A1,
A2, si A3.
Generalizand
relatia (9.1) se obtine ecuatia
fundamentala a lantului de
dimensiuni:
NR = N1
+ N2 + + Nk - (Nk+1 + Nk+2 + .
+ Nn) (2)
sau:
NR = 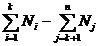 (3)
(3)
in care Ni sunt dimensiunile nominale a
celor i elemente pozitive, iar Nj sunt dimensiunile nominale a celor
j elemente negative.
Valorile
limita ale dimensiunii elementului rezultant se calculeaza astfel:
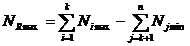 (4)
(4)
respectiv:
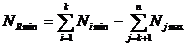 (5)
(5)
Dar
toleranta elementului rezultant TR, prin definitie este:
TR = NRmax - NRmin (6)
si prin inlocuorea relatiilor (9.4) si (9.5) in
relatia (9.6) se obtine ca:
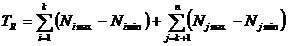 (7)
(7)
sau dupa restrangere:
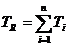 (8)
(8)
Relatia (8) exprima faptul ca toleranta elementului de inchidere este egala cu suma tolerantelor elementelor componente si este definita ca ecuatia fundamentala a tolerantelor
unui lant de dimensiuni. Deci
elementul de inchidere este cel mai putin precis dintr-un lant de dimensiuni ( avand toleranta cea mai mare).
Relatia (8) exprima semnificatia fizica de element colector al erorilor la prelucrarea dimensiunilor lantului
sau de colector al erorilor dimensiunilor de montaj ale lantului.
Pentru
calculul abaterilor elementuluii rezultant pornim de la definitia abaterii superioare (As = Dmax - N) respectiv inferioare (Ai = Dmin -N) si anume:
AsR = NRmax - NR (9)
AiR = NRmin - NR
Apeland la relatiile (9.3), (9.4) si (9.5) in
(9.9) se obtine in final:
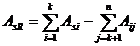 (10)
(10)
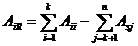
in care Asi,
Aii (i = 1, 2, k) reprezinta abaterile superioare, respectiv inferioare
ale elementelor primare pozitive,
iar Asj, Aij
(j = k+1, , n) reprezinta abaterile superioare
respectiv inferioare ale elementelor
primare negative ale lantului de
dimensiuni.
Se deduc urmatoarele doua
reguli (relatiile 10):
-abaterea superioara a elementul rezultant
AsR este egala cu diferenta dintre suma
algebrica a abaterilor superioare
ale elementelor pozitive (maritoare)
si suma algebrica a abaterilor
inferioare ale elementelor negative (reducatoare);
-abaterea inferioara a elementului rezultant
AiR este egala cu diferenta dintre suma algebrica a abaterilor inferioare ale elementelor pozitive (maritoare) si suma algebrica a abaterilor superioare ale elementelor negative (reducatoare).
Pentru cazul concret initial rezulta:
NR = 50 - (30 + 12) = 8 mm
TR = T1 + T2
+ T3 = 0,20 + 0,05 + 0,07 =
0,32 mm
AsR = 0,1 - (-0,05 + 0) = 0,15
mm
AiR = - 0,1 - (0 + 0,07) =
-0,17 mm
deci elementul rezultant are valoarea :

Se poate verifica toleranta elementului rezultant si cu relatia :
TR = AsR- AiR
= 0,15 - (-0,17) = 0,32 mm.
Obs: Determinarea unui element din lant atunci cand se cunoaste
elementul de inchidere si celelalte elemente
componente ale lantului
Problema
se prezinta cu ajutorul exemplului urmator:
Se considera ecuatia functionala a unui lant:
R = A + A2 - A3 + Ax
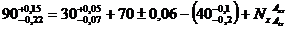
Scriind ecuatiile
dimensiunilor de acelasi
fel, avem:
Pentru dimensiunile nominale: 90 = 30 + 70 - 40
+ Nx 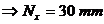
Pentru abaterile superioare: 0,15 = 0,05 + 0,06 + 0,1 + Asx 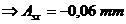
Pentru abaterile inferioare:
-0,22 = -0,07 - 0,06 + 0,2 + Aix 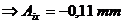
Elementul determinat
va fi:
Ax = 30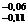 mm
mm
Relatia (8) este indeplinita intrucat avem:
TR =
T1 + T2 + T3 + Tx adica 0,37 = 0,12 + 0,12 + 0,08 + 0,05
Aceasta problema se intalneste frecvent la schimbarea bazei de cotare. In practica se intalnesc situatii cand la intocmirea desenului de piesa,
baza de cotare se alege din punct de vedere functional si sa nu coincida cu baza tehnologica.
In aceasta situatie
se face o recotare a desenului, cand
se alege ca baza de cotare, baza tehnologica.
Noile cote se stabilesc utilizand lanturile de dimensiuni astfel incat
sa fie respectate cotele initiale.
3.2 Metoda probabilistica
In practica s-a observat ca anumite piese componente, desi sunt in afara campului de toleranta pot fi montate
fara ca asamblul sa fie afectat din punct de vedere al calitatii. Acest fapt i-a
facut pe cercetatori sa reexamineze metodele algebrice de
rezolvare a lanturilor de dimensiuni.
S-a constatat ca situatia
limita pentru obtinerea
valorilor Rmax si Rmin
au o probabilitate de realizare extrem de mica, practic nula. E greu de presupus ca la
montarea unui asamblu toate elemetele pozitive se realizeaza la limita maxima
si toate elementele negative se realizeaza la limita minima.
Astfel conditia ca toleranta elementului rezultant trebuie sa fie egala cu suma tolerantelor tuturor elementelor componente trebuie reexaminata din perspectiva statistica.
Din studiul statistic al
dimensiunilor efective dintr-un lot de piese suficient de numeros,
rezulta ca repartitia pieselor
pe diferite grupe de sortare este caracteristica pentru fenomenele intamplatoare.
Pentru exemplificare se va
considera distributia normala a
dimensiunilor (clopotul lui Gauss)
reprezentata in Fig. 6.
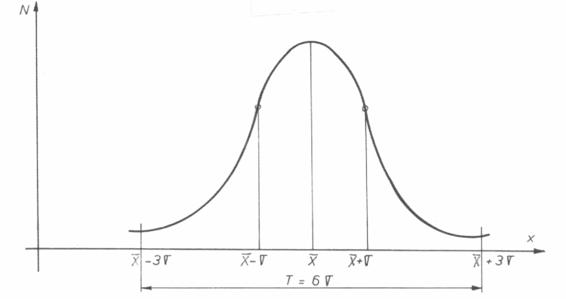
Fig.6
Distributia dimensiunilor in campul de tolerantǎ.
Pentru cazul ideal
forma este simetrica
centrata pe valoarea medie aritmetica a limitelor campului de toleranta, valoarea centrala, X.
Punctele de inflexiune sunt la ± σ, abaterea medie
patratica fata de valoarea centrala.
Se considera ca toate piesele (99.73%) din campul de toleranta sunt cuprinse in domeniul ±3σ = 6 σ
= T.
In cazul combinarii
mai multor fenomene intamplatoare, cum este cazul lanturilor de dimensiuni, este valabila conditia
ca dispersia sumei de marimi intamplatoare, DNR.
este egala cu suma dispersiilor marimilor componente, Di :
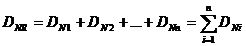 (11)
(11)
Dar dispersia D este patratul lui σ si ecuatia (11) devine:
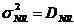 (12)
(12)
de unde:
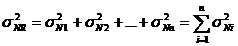 (13)
(13)
sau:
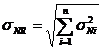 (14)
(14)
unde: - 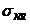 este abaterea medie patratica a dimensiunii elementului
rezultant;
este abaterea medie patratica a dimensiunii elementului
rezultant;
- 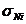 este abaterea medie patratica a celor i = n
dimensiuni componente.
este abaterea medie patratica a celor i = n
dimensiuni componente.
Un important parametru
statistic este abaterea relativa media
patratica exprimata prin relatia:
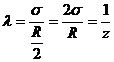 (15)
(15)
unde: - R este amplitudinea intervalului de imprǎstiere a caracteristicii studiate, care in cazul
unei marimi oarecare x, are valoarea
R = xmax - xmin;
- 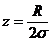 este raportul dintre jumatatea amplitudinii si abaterea
media patratica.
este raportul dintre jumatatea amplitudinii si abaterea
media patratica.
Pentru legea de distributie normala, considerate ca etalon, R = 6σ, respective z=3
si rezulta:
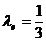 (16)
(16)
Considerand acum amplitudinea intervalului de imprasiere egala cu
toleranta R = T, relatia (15) se scrie:
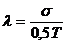 (17)
(17)
Raportul
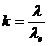 (18)
(18)
se numeste coefficient de imprasiere
relative si caracterizeaza imprasierea dupa o lege de distributie oarecare,
comparative cu legea de distributie normala luata ca etalon.
Daca se inlocuiesc relatiile (15) si (16) in relatia (18) rezulta:
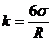 (19)
(19)
Din relatia (17) rezulta:
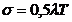 (20)
(20)
Inlocuind relatia 9200 in expresia (14) se obtine dupa transformari:
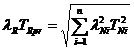 (21)
(21)
sau daca se are in vedere relatia (18) se obtine:
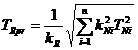 (22)
(22)
In care TRpr reprezinta toleranta probabilǎ (practicǎ sau probabilisticǎ) a dimensiunii
de inchidere a lantului de dimensiuni.
Presupunand ca dimensiunile elementelor primare ale lantului de dimensiuni au pentru valorile lor efective o distributie care se conduce dupa legea normala, dimensiunea de inchidere va avea o distributie dupa aceesi lege si relatia (22) devine:
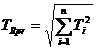 (23)
(23)
pentru ca 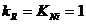 .
.
Daca se presupune de la
inceput ca distributia valorilor efective ale dimensiunilor elementelor primare
ale lantului de dimensiuni se
face dupa legea normala, se poate
scrie:
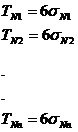 (24)
(24)
iar relatia (14) se scrie astfel:
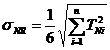 (25)
(25)
rezulta:
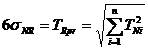 (29)
(29)
Relatie identical cu (23) dar obtinuta pe alta cale.
Relatia (23) arata ca toleranta
dimensiunii elementului resultant calculate prin metoda probabilistica este mai mica decat toleranta determinate prin metoda de maxim sau minim.
Abaterile limita probabile ale dimensiunii de inchidere se pot calcula in functie de abaterile teoretice
determinate prin metoda algebrica
sau in functie de valoarea centrala a dimensiunii de inchidere (Fig.7).
In conformitate cu cele prezentate in Fig.7 se poate scrie:
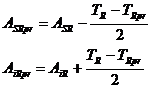 (30)
(30)
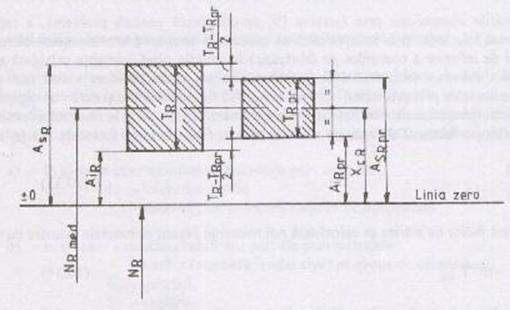
Fig.7
Toleranta algebrica si toleranta probabilistica a dimensiunii de inchidere.
Pentru a intelege mai bine cele
expuse, se reia exemplul din Fig.5 rezolvat prin metoda de maxim si minim.
Toleranta elementului resultant calculate probabilistic este:
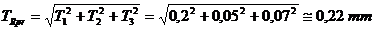
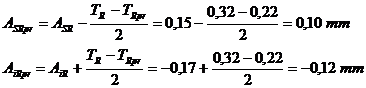
Rezulta valoarea dimensiunii de inchidere calculate cu metoda probabilistaica:
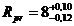
Se observa ca folosind metoda probabilistica, precizia practica a dimensiunii
de inchidere este mai mare pective tolaranta este mai mica, cu un anumit factor de
reducere r , fata de cea rezultata prin metoda de maxim si de minim.
Raportul dintre cele doua tolerante - factorul de reducere-r este:
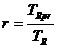 (31)
(31)
In cazul concret al exemplului numeric analizat:
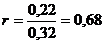
Acest raport dintre cele doua
tolerante este interpretat ca o rezerva de marire a tolerantelor elementelor primare (deci o ieftinire a
costurilor de fabricatie) in
situatia cand toleranta calculata algebric satisface deplin valoarea
elementului de inchidere. Se pot deci
considera valori mai mari la tolerantele elementelor primare,
valori care se impune sa fie determinate si care vor depinde si de felul
imprasierii dimensionale existente la fiecare element primar cat si la
elemental resultant.
Se defineste factorul de marire a tolerantei m, ca fiind inversul factorului de reducere r, astfel:
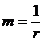 (32)
(32)
Cu acest factor de marire se calculeaza noi tolerante pentru elementele primare cu relatia:
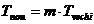 (33)
(33)
In urmatoarea etapa se determina valoarea noua a tolerantei elementului
resultant cu noile tolerante acordate elementelor primare.
La compararea noii tolerante calculate  cu toleranta calculate
probabilistic
cu toleranta calculate
probabilistic 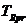 si cu toleranta algebrica
si cu toleranta algebrica 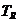 se observa ca:
se observa ca:
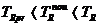 (34)
(34)
Concluzia este ca se pot mari tolerantele elementelor primare cu ajutorul
factorului de marire a tolerantelor
astfel ca toleranta elementului resultant sa fie egala ca valoare, in cazul
calculului probabilistic, cu valoarea data prin metoda algebrica.
Revenind la exemplul analizat,
factorul de marire m este:
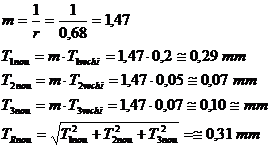
Deci 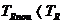 dar foarte
apropiat, iar tolerantele noi acordate elementelor primare au crescut cu 47%.
dar foarte
apropiat, iar tolerantele noi acordate elementelor primare au crescut cu 47%.
3.3 Metoda ajustarii
Metoda este indicata in cazul imbinarii unor piese ce se prelucreaza deosebit de greu si impunerea unor tolerante
mici elementelor componente ar duce
la scumpirea nejustificata a executiei.
Ea consta in
introducerea unui element usor prelucrabil numit element compensator.
La montaj se masoara elementele componente ale lantului si dupa ce s-a calculat dimensiunea elementului compensator Nx , acesta se va prelucra (ajusta) cu aceasi
toleranta ca si elementul rezultant.
Pentru exemplificare se considera ghidajul prismatic din Fig.8.
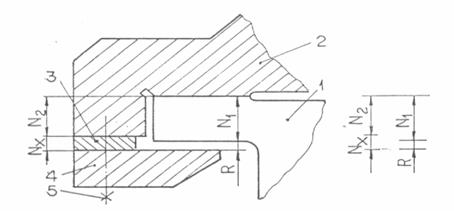
Fig.8 Ghidaj prismatic cu element
ajustabil.
Sania 2 si ghidajul 1 se
vor prelucra cu tolerante economice,
relativ mari pentru dimensiunuile N1 si respectiv N2. Elementul compensator este placa cu fete paralele
de dimensiuni Nx. Conditia
tehnica impune un joc R cuprins intre limite bine determinate.
Metoda presupune cunoscuta
toleranta elementului de
inchidere TR. Aceasta toleranta este relativ mica
si distribuita
dimensiunilor din lant se obtin
tolerante prescrise Tpi
(Tp1, Tp2, ) foarte mici, neeconomice pentru executie.
Tolerantele de fabricatie Tfi (Tf1,
Tf2, ) se stabilesc
tinandu-se seama de posibilitatile tehnice si economice de realizare. In acest caz, toleranta elementului de inchidere TRf
este mai mare decat
toleranta TR prescrisa.
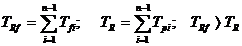 (35)
(35)
Surplusul de toleranta 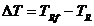 urmeaza sa fie compensat la montaj prin prelucrarea unui element din lant cu multa precizie, numit element
compensator. Elementul compensator
trebuie prevazut la proiectare cu adaus de prelucrare suficient de mare si el nu trebuie sa
apartina altor lanturi de
dimensiuni.
urmeaza sa fie compensat la montaj prin prelucrarea unui element din lant cu multa precizie, numit element
compensator. Elementul compensator
trebuie prevazut la proiectare cu adaus de prelucrare suficient de mare si el nu trebuie sa
apartina altor lanturi de
dimensiuni.
Metoda prezinta o serie de dezavantaje, cum sunt:
- necesita munca calificata la
prelucrarea elementului compensator, de care depinde calitatea asamblarii;
- metoda nu
poate fi aplicata la fabricatia de serie
intrucat nu se cunoaste timpul de ajustare.
Metoda se
recomanda a fi aplicata pentru lanturi
de dimensiuni cu multe elemente,
la productia individuala sau
de serie mica.
Exemplu:
Pentru lantul de
dimensiuni din Fig.9, toleranta elementului de inchidere TR = 115 μm si repartizata dimensiunilor din lant se obtin
tolerantele Tpi:
Tp1 = 15 μm ; Tp2 = 18 μm ; Tp3 = 14
μm ; Tp4 = 20 μm ; Tp5 = 18
μm
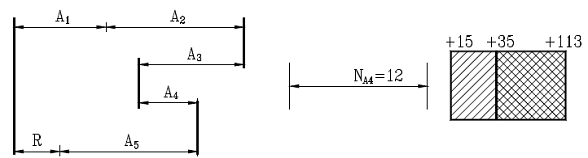
Fig.9 Metoda
ajustarii.
`Pe baza posibilitatilor
tehnico-economice de executie,
sunt necesare tolerantele:
Tf1 = 30 μm ; Tf2 = 40 μm ; Tf3 = 35 μm ; Tf4
= 38 μm ; Tf5 = 50 μm
Se
stabileste ca elementul A4 sa
fie element compensator.
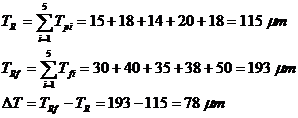
Daca elementul A4 prescris are marimea
A4 = 12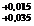 mm, marimea lui pentru a compensa pe ΔT = 78 μm este
12
mm, marimea lui pentru a compensa pe ΔT = 78 μm este
12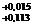 mm, urmand ca la montaj, prin ajustare, sa fie inlaturat materialul (Fig. 7.10.b) corespunzator
spatiului dublu hasurat.
mm, urmand ca la montaj, prin ajustare, sa fie inlaturat materialul (Fig. 7.10.b) corespunzator
spatiului dublu hasurat.
3.4 Metoda reglarii
Rezovarea lantului de dimensiuni prin
aceasta metoda presupune executia
dimensiunilor primare ale lantului
la tolerante economice urmand ca dimensiunea elementului de inchidere sa se obtina, in limitele
prescrise, prin modificarea
(reglarea-fara prelucrare) unei dimensiuni
componente in sensul dorit, formandu-se astfel un element compensator sau de reglare.
Compensatoarele pot
fi:
fixe, difera intre ele in directia se compensare cu o
valoare care sa asigure realizarea tolerantei (ex. inele - Fig.10, placi,
discuri, etc.);
|
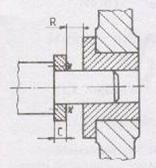
Fig.10 Compensator fix.
|
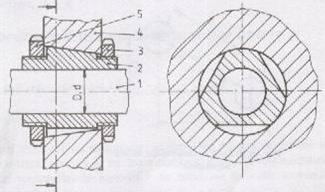
Fig.11 Compensator mobil periodic.
|
In Fig.11 reglarea periodica a
jocului intre arborele 1 si corpul lagarului 2 cu suprafete conice exterioare
in carcasa 4 se realizeaza de catre piulitele 3 si 5.
mobile
|
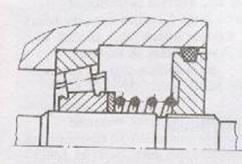
Fig.12 Compensator mobil continuu.
|
a) cu reglare (compensare) periodica, - precizia dimensiunii de inchidere se restabileste periodic (ex. lagare conice de
alunecare - Fig.11, pene, piulite conice elastice, etc.);
b) cu reglare continua - precizia obtinuta
initial este mentinuta
continuu, automat (ex: Fig.12,
compensator mobil continuu cu arc elicoidal pentru asigurarea jocului la
rulmenti radiali - axiali cu role conice).
|
De
obicei, compensatoarele fixe se
utilizeaza la asamblare in productia
individuala si de serie mica, intrucat, pana la obtinerea
dimensiunii de inchidere in limitele prescrise sunt necesare montari si demontari repetate.
Compensatoarele
mobile se aplica in toate tipurile de productie.
Metoda reglarii are dezavantajul unei precizii mai scazute
decat metoda ajustarii dar avantajul unei productivitati mai mari
la montaj.
3.5 Metoda sortarii sau a asamblarii
selective
Sunt cazuri de montaj in care elementele componente sunt combinate
convenabil astfel incat si piesele rebutate sa poata realiza toleranta impusa elementului
de inchidere.
Alteori elementele de
inchidere au tolerante relativ mici, ceea ce impune tolerante mult
mai mici elementelor componente astfel incat prelucrarea acestora devine neeconomica.
Metoda sortarii - asamblarii selective presupune executarea pieselor la tolerante economice si sortarea elementelor componente, pe grupe de dimensiuni
si combinarea acestora intre grupe de acelasi rang, astfel incat elementul de inchidere sa se obtina la precizia dorita.
Metoda se preteaza,
evident, numai la productia de serie.
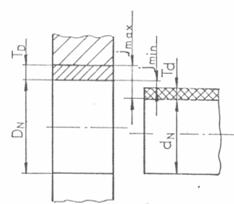
Pentru exemplificare se considera cazul unui ajustaj cilindric
prezentat in Fig.13.
|
a)
|
b)
|
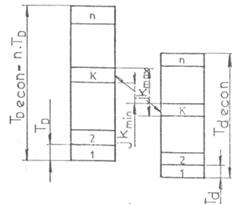
Fig.13 Metoda
sortarii: a) ajustajul; b) toleranta economica.
Din conditiile de
functionare au rezultat jocuri minime si jocuri maxime foarte apropiate si, in consecinta, tolerante foarte mici
(jmax-jmin=TD +Td ).
Prelucrarea arborilor si
alezajelor cu aceste tolerante devine
neeconomica sau chiar nerealizabila
practic cu mijloacele unei
anumite intreprinderi. Exemplul este tipic
pentru productia de rulmenti.
In aceasta situatie,
piesele se vor prelucra cu tolerante economice,
Tecon care vor fi de n ori mai mari decat tolerantele impuse. Dupa prelucrare cele doua loturi de piese se masoara si se impart in "n' grupe pe intervale de
dimensiuni, astfel incat in grupa de ordinul k limitele sa fie;
Dmin = D + (k - 1 ) TD si
Dmax
= D +k TD, pentru alezaje
si respectiv,
dmin = d + (k - 1 ) TD si
dmax
= d + k TD, pentru arbori ,
dupa cum se vede in Fig.13b.
Jocurile limita impuse
asamblarii (Fig.13 a ) sunt :
jmin = D N -(d N +Td ) si jmax = (D N +T D ) -dN (36)
Calculand jocurile pentru grupa de sortare 'k' se obtine succesiv:
jkmin = D N +(k-1) TD-(d N
+kT d ) si jkmax = D N +kT D -dN - (k-1) Td
sau
jkmin = jmin +(k-1) (TD-T d
) si jkmax = jmax + (k-1)
(T D -Td ) (37)
Se constata urmatoarele:
a)
pentru cazul
in care elementele componente au aceeasi toleranta (TD
= Td), jocurile maxime si
minime nu depind de ordinul grupei de sortare;
b)
pentru cazul cand
tolerantele elementelor componente
sunt diferite (TD ≠
Td), jocurile minime si
maxime variaza de la o grupa la alta ( sunt functii de k) si sunt diferite
de cele impuse pentru primele ;k
≠ 1; (metoda nu poate fi aplicata)
c)
pentru a putea fi aplicata metoda sortarii este absolut necesar sa se impuna toleranta comuna
T ' egala cu cea mai mica dintre TD si Td.
T '= min , (38)
O consecinta a
acestei conditii este ca si tolerantele adoptate pentru executia fiecarui lot trebuie sa fie egale intre ele si mai mari sau egale cu cea mai mare
toleranta economica.
Tecon = max (39)
In acest caz jocurile minime
si maxime nu mai depind de ordinul grupei de sortare
si sunt cuprinse in limitele impuse:
jmin
jkmin jkmax jmax (40)
d)
daca se impun
de la inceput tolerante egale TD = Td,
exista pericolul ca dupa sortare grupele de sortare de acelasi
ordin sa nu
contina numere egale de piese astfel incat diferenta sa fie inutilizabila Aceasta situatie poate fi preintampinata numai in cazul
productiei de serie mare cand repartitia elementelor pe grupe de sortare se apropie de distributia normala (curba lui Gauss).
e)
in cazul tolerantelor inegale TD
≠ Td, exista posibilitatea
compensarii numarului
de piese dintr-o grupa de
sortare de ordinul k cu piesele de dimensiuni minime din grupa k+1 si piesele de dimensiuni maxime din grupa k - 1; in exemplul din Fig.14, TD > T'.
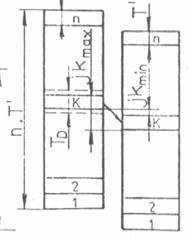
Fig.14. Sortarea pieselor cu tolerante inegale.
Modificarea tolerantei de executie
a pieselor nu afecteaza tolerantele de forma si de pozitie si nici rugozitatea suprafetelor.
Aplicarea metodei trebuie sa fie hotarata in urma
unui studiu tehnico-economic
temeinic intucat ea implica cheltuieli
suplimentare cu masurarea si sortarea care
trebuie sa fie recuperate din economiile cu cheltuielile de productie.
Metoda este aplicabila
numai lanturilor de dimensiuni cu 2
- 3 elemente componente si numai
daca fiecare element intervine in lant cu o singura dimensiune a sa.
Pentru exemplificarea
metodei, se considera ajustajul cu strangere prezentat in Fig.15: Ø30 Ø30
Ø30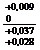
Se observa ca: TD = Td
= 0,009 mm.
Smax = es -
EI = 0,037 mm
Smin = ei -
ES = 0,019 mm
Ts = Smax
- smin = 0,018 mm
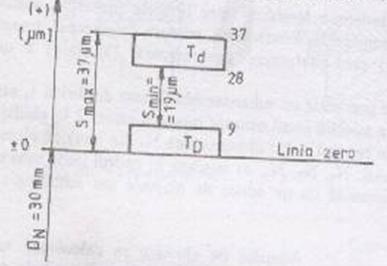
Fig.15 Ajustaj Ø30 H5/r5.
Daca marim tolerantele initiale, de exemplu,
de n = 5 ori, se obtin:
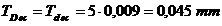
In acest caz pe
desenele de executie ale arborelui si alezajului se vor prescrie urmatoarele abateri:
pentru alezaj: Ø30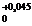
pentru arbore: Ø30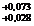
Dupa
executia pieselor in cadrul tolerantelor
economice, se masoara bucata cu bucata arborii si alezajele si se sorteaza in 5 grupe, conform Fig. 16
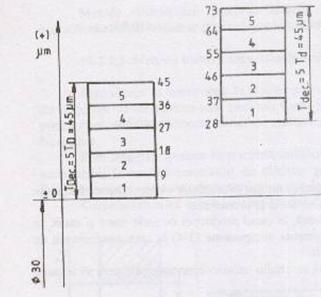
Fig.16 Sortarea pe grupe a lotului
prelucrat in tolerante economice.
Asambland arbori cu alezaje din grupe de acelasi rang se obtin urmatoarele
strangeri:
Smax1
= es1 - EI1 = 0,037-0 = 0,037 mm
Smin1
= ei1 - ES1 = 0,028 - 0,009 = 0,019 mm
.
.
.
Smax5
= es5 - EI5 = 0,073-0,036 = 0,037 mm
Smin5
= ei5 - ES5 = 0,064 - 0,045 = 0,019 mm
Deci aceleasi valori prescrise initial ajustajului.
Rezolvarea lanturilor de dimensiuni
liniare neparalele
Se
intalnesc cazuri cand elementele lantului nu mai sunt paralele, fiind inclinate unele fata de
altele, insa toate fiind situate intr-un plan.
Aceste
lanturi se transforma in lanturi de dimensiuni paralele prin proiectarea elementelor neparalele
dupa directia celor paralele. Dupa transformare se aplica metodele de calcul de la lanturile de dimensiuni paralele.
Pentru exemplificare consideram lantul de dimensiuni care se poate forma in cazul unui angrenaj (Fig.17).
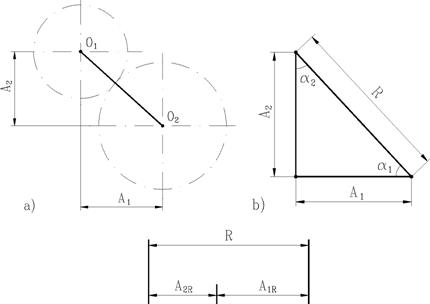
Fig.17 Lant de dimensiuni liniare neparalele.
Elementele A1 si A2 se proiecteaza pe directia
elementului R, transformandu-se in lant cu elemente paralele (A1R,
A2R):
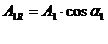
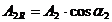 (41)
(41)
R = A1 cosα1
+ A2 cos α2 (42)
La
aplicarea metodelor de calcul, dimensiunile nominale, abaterile si tolerantele elementelor lantului se
inmultesc cu coeficientii de transfer ki = cosαi , si se poate scrie
relatia:
R= k1A1
+ k2A2 (43)
Iar prin generalizare pentru n dimensiuni:
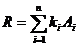 (44)
(44)
5 Lanturi
de dimensiuni unghiulare
Lanturile
de dimensiuni unghiulare sunt formate din elemente unghiulare cu varf comun sau cu varfuri diferite (Fig.18
Lanturile de dimensiuni cu varfuri diferite se intalnesc de obicei la determinarea abaterilor de
pozitie (perpendicularitate, paralelism etc.) dintre axe si
suprafete.
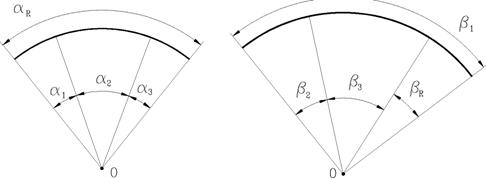
Fig.18 Lanturi de
dimensiuni unghiulare
6 Aplicatii ale lanturilor de
dimensiuni.
6.1 Asamblarile cilindrice in trepte
Suprafetele cilindrice in trepte ale arborilor si alezajelor
rezulta in general excentrice, din cauza
prelucrarii lor prin treceri diferite. Abaterile de pozitie ingreuneaza
interschimbabilitatea. Acolo unde
interschimbabilitatea nu este obligatorie, prelucrarea alezajelor se executa numai in faza de montaj
astfel incat excentricitatea alezajelor
sa fie minima.
In cazul in care interschimbabilitatea este impusa,
abaterile de la coaxialitate
inevitabile prelucrarii impun
jocuri mai mari ca de obicei intre arbori si alezaje.
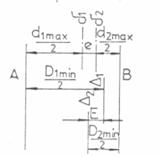
In Fig.19a
este reprezentata imbinarea dintre
un arbore si un alezaj cilindric in doua
trepte. Toate notatiile referitoare la arbore sunt cu litere mici, iar la
alezaj cu litere mari.
|
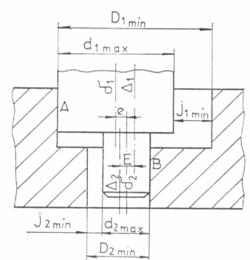
a)
|
b)
|
Fig.19 a) Asamblari cilindrice in trepte; b) lantul de
dimensiuni.
Pentru a se putea asigura
rotirea intre arbore si alezaj se va considera cazul cel mai defavorabil,
cand arborele este executat cu
diametrele d1 si d2 la valori maxime, iar alezajul cu diametrele D1
si D2 la valorile minime si excentricitatile E si e sunt diametral opuse.
In
acesta situatie distanta intre
generatoarele A si B pentru arbore lAB trebuie sa fie mai mica sau cel mult
egala cu distanta pentru alezaje.
Lantul
de dimensiuni limitat de cele doua generatoare A si B este reprezentat in Fig.19b.
Conditia de inchidere a lantului de dimensiuni si conditia
de asamblare si rotire intre arbore si alezaj este:
d1 max + 2e +d2max D1min
-2E +D2 min (45)
sau inca;
2( e + E ) (D1min
- d1 max ) + (D2 min - d2max ). (46)
Tinand
cont ca diferentele Dmin
- d max reprezinta jocurile
minime, relatia (46) se mai poate scrie:
e + E 1/2
(j1min + j2 min ) (47)
Relatia 47 exprima conditia ce se impune asamblarilor in doua trepte si anume ca suma abaterilor de la coaxialitate trebuie sa fie mai mica cel mult egala cu media
aritmetica a jocurilor minime.
Se impune observatia ca daca jocurile minime sunt nule sau negative (cazul strangerilor) conditia nu poate fi satisfacuta
intrucat excentricitatile
sunt pozitive. Din aceasta cauza, in general se evita astfel
de asamblari sau se alege pentru una din trepte un joc
minim mai mare decat suma abaterilor de la coaxialitate ce se pot obtine in
conditii economice.
6.2 Asamblarea
placilor cu alezaje cilindrice dispuse liniar
Pentru a se asigura interschimbabilitatea placilor cu alezaje dispuse liniar
este necesar ca distanta dintre axele alezajului sa se incadreze in anumite limite in functie de tolerantele diametrelor gaurilor si bolturilor.
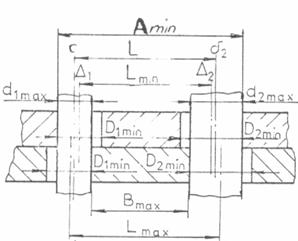
Pentru
determinarea conditiei de asamblare pentru doua alezaje se considera
Fig. 20.
|
a)
|
b)
|
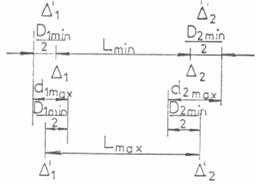
Fig.20 a)
Asamblari cilindrice netede; b) lantul de dimensiuni.
Cazul cel mai defavorabil este cand alezajele
sunt executate la diametrul minim, D min
si arborii la diametre maxime,
d max .
Scriind conditia de inchidere a lantului
de dimensiuni din Fig.20b se obtine:
D1 min +2Lmin +D2min 2d1max - D1min
+ 2Lmax - D2min + 2d2max (48)
sau,
Lmax
-Lmin D1 min -d1max
+ D2min - d2max . (49)
Relatia
49 se mai poate scrie:
TL
j1min + j2 min (50)
In cazul in
care jocurile minime ale alezajelor sunt egale se obtine:
TL 2jmin
(51)
Extinzand
rezultatele pentru cazul unor
'n'ajustaje (multiple) dispuse
liniar rezulta pentru distanta
intre primul si al n - lea ajustaj, Ln toleranta. TLn
:
TLn 2jmin (52)
Tinand
cont ca ajustajele sunt dispuse echidistant la distanta L si ca formeaza un lant de dimensiuni se obtine:
( n - 1 ) TLn 2jmin (53)
Un caz
deosebit de ajustaje dispuse liniar il prezinta situatia cand sprijinul
se face pe o suprafata comuna.
Este cazul intalnit la penele transversale;
cand sprijinul se face pe aceeasi suprafata, evident jocul minim este egal cu zero, astfel ca relatia 52 devine:
TL jmin
= Dmin - d max (54)
6.3 Asamblarea placilor cu alezaje cilindrice dispuse in contur
poligonal.
Se
considera asamblarea a doua flanse cu 'n' gauri
dispuse in varfurile unui poligon regulat, ca in Fig.21.
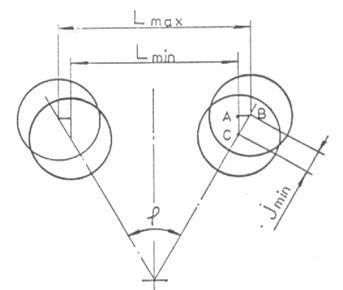
Fig.21 Asamblari cilindrice dispuse pe contur
poligonal.
Se considera
ca alezajele celor doua placi nu au erori de divizare ci numai erori ale razelor
cercurilor circumscrise
poligoanelor.
Tinand cont ca cercurile de dispunere a
gaurilor trebuie sa fie concentrice,
pentru conditia de asamblare este valabila relatia 54
care in acest caz va fi :
BC = jmin
= Dmin - d max (55)
Dar tolerantele la distanta
dintre axele alezajelor, TL in acest caz va fi:
TL = 2 AB
= 2 jmin x sin j
sau
TL = 2 jmin
x sin t/n
. (56)










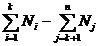 (3)
(3)
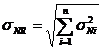 (14)
(14)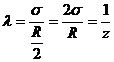 (15)
(15)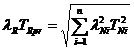 (21)
(21)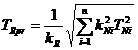 (22)
(22)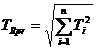 (23)
(23)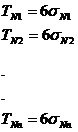 (24)
(24)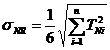 (25)
(25)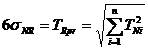 (29)
(29)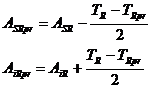 (30)
(30)