MODELARE SI SIMULARE
I
Un sistem este un ansamblu organizat de componente (subsisteme)
interdependente, capabil sa raspunda, sub actiunea a
diversi stimuli, unui anumit scop, cu anumite performante,.
Sistem de productie = ansamblul se posturi de lucru, masini - unelte, operatori umani,
personal de intretinere.
Proces de productie = totalitatea fenomenelor (deplasari, transformari,
asamblari, activitati umane etc) ce au loc in sistemul de
productie in scopul obtinerii produselor finite.
Clasificarea sistemelor
deschise / inchise
liniare / neliniare
mari / complexe
deteministe / nedeterministe (stockastice, fuzzy)
discrete / continue
hibride
instruibile
Tipuri de modele
fizice
matematice ( studiul
ului)
procedurale
Etapele realizarii unui model de simulare
stabilirea obiectivelor (definirea problemei);
colectionarea
si analiza primara a datelor
formularea modelului de simulare;
estimarea variabilelor de intrare;
estimarea caracteristicilor operative;
descrierea
algoritmului si scrierea programului;
validarea modelului;
planificarea experimentelor;
simularea;
analiza rezultatelor.
Stabilirea obiectivelor
- criterii - tehnico-economice
- experienta
incredere
client
oportunitate
volum
de munca
profit
stabilitate
solutii
Formularea problemei
Un manager vrea sa
aleaga acel al
activitatii sale care va fi cel mai performant in atingerea scopului
firmei sale.
In judecarea eficientei
diferitelor decizii posibile, trebuie sa se foloseasca anumite
criterii pentru masurarea performantei activitatii in discutie.
Este indicat sa se
urmareasca etapele
stabilirea criteriului de eficienta
selectarea
unei multími de alternative posibile
determinarea
unui model care sa fie folosit si a valorilor parametrilor procesului
determinarea
alternativei care optimizeaza criteriul de la pct. 1
Problemele lumii reale tind
sa fie deosebit de complexe. In orice situatíe empirica
exista nenumarati factori inerenti. Orice potential al actiunii
initiaza un lant de cauza.
Mintea umana nu poate
considera toate aspectele empirice ale problemei. Anumite atribute ale
problemei trebuie ignorate ca sa se poata lua o decizie. Decidentul
trebuie sa identifice factorii cei mai relevanti pentru
problema.
Abstractizarea si
simplificarea sunt factori necesari in rezolvarea oricarei probleme umane.
Stabilirea obiectivelor
obiectivul trebuie sa fie realizat
sa se constientizeze caracterul probabilistic
Construirea modelului
Dupa selectarea
factorilor relevanti de catre decidenti, acestia sunt
combinati in mod logic astfel incat sa formeze un model al problemei
actuale.
Un model este o reprezentare simplificata a unei situatii
empirice. Modelul reduce complexitatea si pastreaza comportarea
esentiala a fenomenului natural, avand un numar redus de factori care
sunt legati intre ei prin relatii simplificate.
Avantajele unui model simplu:
economie de timp si idei
poate
fi inteles mai usor si repede de catre decident
Obiectivul decidentului
nu este sa construiasca un model cat mai apropiat posibil de
realitate, deoarece un astfel de model ar lua mult timp pentru concepere.
Dupa ce modelul a
fost construit se pot obtine concluziile prin intermediul actiunilor
logice. Decidentul isi bazeaza actiunile sau deciziile pe aceste
concluzii.
Concepte de baza in modelare
Primul pas in construirea unui
model este stabilirea factorilor si variabilelor pe care decidentul le
considera importante. Factorii, variabile de decizie, variabile exogene,
restrictii, masuri ale performantei, variabile intermediare.
Variabile de decizie acele variabile pe care le controleza
decidentul
reprezinta alegerile alternative pentru decident.
Variabile exogene sunt importante in problema de decizie,
dar sunt controlate de factori externi sferei decidentului.
Restictiile legate de capacitatea de productie,
resurse, limitari legislative, politica firmei, etc.
Masuri ale performantei expresii cantitative ale
obiectivului, scopul ce trebuie atins in acea activitate.
Variabile intermediare necesare pentru includerea tuturor factorilor
importanti in problema de decizie lega factorii de cost si de castig
leaga variabilele de decizie si
exogene de masuri ale performantei.
Exemplu
Problema de transport
Se considera
ca exista n depozite, Di, cu capacitati  ,
, 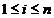 , si m centre de consum, Cj, cu necesitati
, si m centre de consum, Cj, cu necesitati 
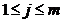 . Fie
. Fie 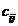 costul
unitar de transport de la depozitul
costul
unitar de transport de la depozitul 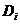 la centrul de consum
la centrul de consum 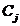
Sa se determine un plan
de transport pentru un produs omogen astfel incat cheltuielile totale de
transport sa fie minime si sa fie satisfacute toate
cererile.
Modelarea problemei
Notam cu: 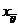 - cantitatea transportata de la depozitul
- cantitatea transportata de la depozitul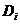 la centrul
de consum
la centrul
de consum 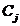
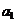
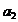 . . . . .
. . . . . 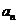
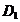
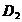 . . . . .
. . . . . 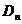
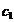
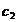 . . . . .
. . . . . 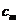
Ipoteza simplificatoare 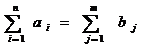 = relatie de echilibru, adica
= relatie de echilibru, adica
a a
disponibilul
= necesarul
oferta = cererea
Functia
obiectiv este data
de cheltuielile totale
de transport, anume
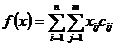
Restrictiile
problemei
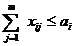
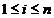 , cantitatea care pleaca de la depozitul Di nu poate depasi
capacitatea depozitului,
, cantitatea care pleaca de la depozitul Di nu poate depasi
capacitatea depozitului,
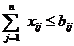
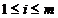 , cantitatea transportata la centrul de
consum Cj nu poate depasi necesarul acestui
centru,
, cantitatea transportata la centrul de
consum Cj nu poate depasi necesarul acestui
centru,
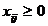
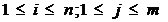 , cantitatea
transportata de la un deposit la un centru de consum este nenegata.
, cantitatea
transportata de la un deposit la un centru de consum este nenegata.
S-a obtinut urmatorul model matematic
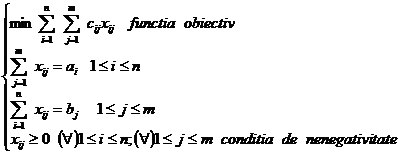
Acesta este un model liniar, determinist.
Colectionarea si analiza primara a datelor
familiarizarea
executantului cu sistemul ce urmeaza a fi modelat,
identificarea
variabilelor de stare si a parametrilor relevanti,
identificarea
factorilor perturbatori, a criteriilor de periodicitate,
a nu
se neglija informatiile obtinute pe parul stabilirii obiectivului.
Formularea modelului de simulare

Estimarea variabilelor de intrare
achizitia
datelor,
prelucrarea
statistica primara,
determinarea
modurilor de variatie in timp.
Estimarea caracteristicilor operative
determinarea
expresiilor matematice, relatiilor procedurale intre variabilele de
intarare, parametrii si variabilele de iesire
expresia
matematica se determina, in general, prin analiza de regresie.
Exemplu
Evolutia timpilor la proba olimpica de 200m barbati [1]
La proba olimpica de atletism de 200m atat la
barbati cat si la femei timpii inregistrati au fost mai
buni de la o editie la alta. Se pune problema
- daca exista o limita sub care nu
se poate cobori
- daca timpii inregistrati la femei va
fi mereu inferior celor inregistrati la baieti?
In [1] sunt inregistrati timpii la proba de
200m barbati incepand cu 1900, iar pentru femei incepand cu1948
si aceste date sunt in tabelele de mai jos.
Medaliatii cu aur la 200m barbati
|
Anul
|
Nume
|
Tara
|
Timpul in secunde
|
|
W. Tewksbury
|
USA
|
|
|
A. Hahn
|
USA
|
|
|
R. Kerr
|
Canada
|
|
|
R.Craig
|
USA
|
|
|
A. Woodring
|
USA
|
|
|
J. Scolz
|
USA
|
|
|
P. Wiliams
|
Canada
|
|
|
E. Tolan
|
USA
|
|
|
J. Owens
|
USA
|
|
|
M. Patten
|
USA
|
|
|
A. Stansfield
|
USA
|
|
|
R. Marrow
|
USA
|
|
|
L. Berruti
|
Italia
|
20,5
|
|
H. Carr
|
USA
|
|
|
T. Smith
|
USA
|
|
|
V. Borsov
|
URSS
|
|
|
D. Quarrie
|
Jamaica
|
|
|
P. Mennea
|
Italia
|
|
|
C. Lewis
|
USA
|
|
|
J. DeLoch
|
USA
|
|
|
M. Marsh
|
USA
|
|
|
M. Johnson
|
USA
|
|
|
K. Kenteris
|
Grecia
|
|
Medaliatele cu aur la 200m femei
|
Anul
|
Nume
|
Tara
|
Timpul in secunde
|
|
F. Blankers-Koen
|
Olanda
|
|
|
M. Jackson
|
Australia
|
|
|
B. Cuthbert
|
Australia
|
|
|
W. Rudolph
|
USA
|
|
|
E. McGuire
|
USA
|
|
|
I. Szewinska
|
Polonia
|
|
|
R. Stecher
|
Germania de Est
|
|
|
B. Eckert
|
Germania de Est
|
|
|
B. Wockel
|
Germania de Est
|
|
|
V. Brisco-Hooks
|
USA
|
|
|
F. Griffith-Joiner
|
USA
|
|
|
G. Torrence
|
USA
|
|
|
M-J. Perec
|
Franta
|
|
|
M. Jones
|
Italia
|
|
Datele acestea constituie ceea ce se numeste
o serie de timp. Incepand din 1968 masuratorile s-au putut face la
sutime de secunda. Daca 200m sunt alergati in 20 secunde, viteza
atletului este de 10m/s si atunci in 0.01 secunde se parcurg 10 cm. La fotografie
se poate vedea diferenta la sosire. Nu este realist sa credem ca ar
putea sa fie observata distanta para intr-o miime de
secunda.
Raspunsul la cele doua intrebari se
poate da facand predictie
asupra tendintei datelor. Daca folosim Excel si aproximam
cu o dreapa datele observam ca dreptele se intersecteaza si
dupa aceea timpii fetelor ar fi mai mic decat cel al barbatilor.
Modelul linear nu este insa acceptabil pe o perioada mai mare de timp
deoarece dupa un numar de ani, distanta ar fi para in 0
secunde! Atunci se cauta alte modele care sa reprezinte mai bine
comportarea acestui fenomen.
Validarea modelului
A nu se confunda cu corectitudinea cu care
transpunerea software descrie modelul original.
Validare prin simularea - unor situatii anterioare
- unor situatii cu consecinte
previzibile
Planificarea experimentelor
Modalitati de realizare a programului de simulare
intr-un
mediu (limbaj) de programare,
prin
transpunere in modele abstracte si utilizarea de software specializat,
cu
utilizarea de software de simulare dedicat.
MODELARE SI SIMULARE
II
Prelucrarea statistica a datelor
Notiuni de statistica descriptiva
Populatia
statistica este multime,
grup, colectivitate, notata cu P.
Volumul
populatiei se
noteaza cu |P|, iar un element  se numeste individ.
se numeste individ.
Caracteristica
populatiei este o trasatura
comuna pentru indivizii populatiei. Ea poate fi
cantitativa nume de variabila aleatoare,
calitativa atribut.
Statistica
matematica este
ramura matematicii aplicate care se ocupa cu studiul caracteristicilor
populatiilor.
Colectarea informatiilor poate fi: exhaustiva
sau prin esantionare. Esantionul trebuie sa fie reprezentativ,
adica sa pastreze structura populatiei din care provine.
Tabelul
statistic este o forma
de prezentare a rezultatelor prelucrarii statistice prin care se
caracterizeaza populatia. Tabelele pot fi
simple:
cu populatie
negrupata, sau
pe
grupe, adica populatia este impartita in grupe
dupa o singura caracteristica. Lungimea intervalului se poate
calcula cu formula lui H. A. Sturges:
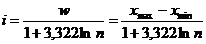 .
.
Combinate,
adica populatia e despartita in grupe dupa
doua sau mai multe caracteristici,
cu
dubla intrare in care se reprezinta frecvente bidimensionale.
(ex: facultate si proc
student)
Reprezentarea grafica a repartitiilor de frecventa
Histograma
este o reprezentare
grafica a datelor, astfel incat pe orizontala se reprezinta intervalul
de valori, iar pe verticala frecventa valorilor.
Exemplu
Salariul orar pentru 115 muncitori (in euro):
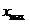 = ;
= ;
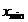 =
=
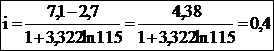
|
Salariul
orar
|
Nr.
aparitii
|
Frecventa
relativa
|
Frecventa
cumulativa
|
|
2,7
- 3,1
|
9
|
0,078
|
0,078
|
|
3,2
- 3,6
|
14
|
0,12
|
0,2
|
|
3,7
- 4,1
|
18
|
0,156
|
0,35
|
|
4,2
- 4,6
|
21
|
0,18
|
0,53
|
|
4,7
- 5,1
|
23
|
0,2
|
0,73
|
|
5,2
- 5,6
|
16
|
0,13
|
0,87
|
|
5,7
- 6,1
|
10
|
0,08
|
0,96
|
|
6,2
- 6,6
|
4
|
0,03
|
 1 1
|
Poligonul frecventelor
Estimatie
Functia de repartitie
empirica
rezulta din date de masuratoare
Ex x 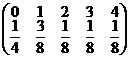
Fc(x) = 0 , 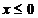
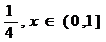
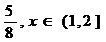
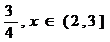
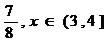
= 1 , 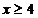
Teorema lui Glivenko (stabileste legatura intre functia
de repartitie empirica si functia de repartitie
teoretica)
Probabilitatea 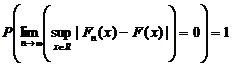
Estimator
pentru parametrul 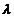 , o
functie
, o
functie 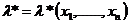
Obs 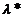 este o variabila aleatoare
este o variabila aleatoare
Estimator consistent 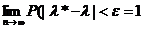
Estimator corect:
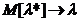 ;
; 
Deplasarea
= 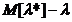
nedeplasat 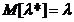
Estimator
absolut corect 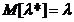 ;
; 
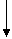 Inegalitatea
lui Cebisev
Inegalitatea
lui Cebisev 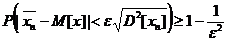
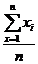
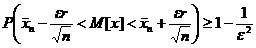
interval care contine media teoretica (interval
de incredere)
Prelucrarea datelor
Datele experimentale (provenite din
masuratori) pot fi afectate de erori
de tipul:
aberante
- grosolane
datorate unor erori grave facute de om sau defectiune de aparat
sistematice
provin din punerea la o incorecta a
unor componente ale aparatului cu care se fac masuratorile
aleatoare
generate de natura aleatoare a
fenomenului analizat
Inainte de efectuarea unor analize ale acestor
date se fac anumite teste testul statistic este un criteriu de impartire a
domeniului valorilor variabile in doua regiuni. Se accepta o ipoteza
asupra v.a sau se respinge. Aceasta ipoteza se numeste
ipoteza nula.
Domeniul in urma caruia-se respinge ipoteza
nula se noteaza cu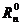 (domeniul critic)
(domeniul critic)
-se
accepta ipoteza nula se noteaza cu 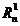
Risc = de genul I 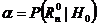 resping ipoteza
resping ipoteza 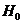 cand era adevarata
cand era adevarata
= de
genu II 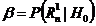 accepta ipoteza
accepta ipoteza 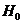 cand era falsa
cand era falsa
In general pentru 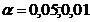
Etapele verificarii ipotezei statistice
Enuntarea ipotezei
Se specifica 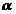 si
si 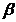
Se
determina ce valoare a unei anumite statistici formeaza reg
critica
Se
calculeza val statisticii din selectie
Se
accepta sau nu ipoteza dupa cum valoarea obtinuta din
statistica (4) este in afara sau inauntrul reg critice
Identificarea valorilor afectate de
erorile aberante si eliminarea lor
Testul Chauvenet Fiind date valorile, 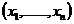 se considera
ca valoarea
se considera
ca valoarea 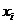 este afectata
de erori aberante daca verifica relatia:
este afectata
de erori aberante daca verifica relatia:
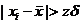
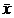 media aritmetica a valorilor
observate
media aritmetica a valorilor
observate 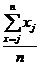
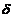 = abaterea standard a valorilor observate
= abaterea standard a valorilor observate
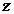 = din tabele
= din tabele
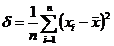
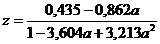
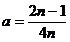
Daca in urma aplicarii testului una
din valori este afectata de erori aberante, valoarea respectiva se
elimina din esantion. Se recalculeaza 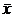 si
si 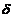 pentru valorile ramase si se reia criteriul.
pentru valorile ramase si se reia criteriul.
Tema 1. Scrieti un program (C++) pentru testul Chauvenet. Datele de
intrare se iau dintr-un fisier text.
Ex: In simularea unui system real se
urmareste repartitia numarului de piese realizate de o
masina intr-o zi. Pe parul a 6 saptamani se
inregistreaza urmatoarele cantitati:
|
sapt
|
L
|
Ma
|
Mi
|
J
|
V
|
sapt
|
L
|
Ma
|
Mi
|
J
|
V
|
|
I
|
|
|
|
|
|
V
|
|
|
|
|
|
|
II
|
|
|
|
|
|
V
|
|
|
|
|
|
|
III
|
|
|
|
|
|
VI
|
|
|
|
|
|
Sa se verifice daca acest esantion
are valori aberante si daca exista, sa le eliminam.
MODELARE
SI SIMULARE
III
Prelucrarea
datelor experimentale
Datele sunt
afectate de erori:
aberante
(le depistam cu criteriul Chauvenet)
sistematice
(testul Young)
aleatoare
(daca datele sunt normale, variabila aleatoare normala-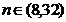 -testul Massy
-testul Massy
-n>50 -testul 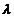
Testul lui Young
Fiind dat un sir de date experimentale 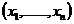 , se
calculeaza
, se
calculeaza 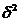
P1. 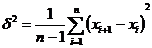
Marimea 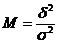
P2. Se compara M cu valoarea critica
(VCI) inferioara si valoarea critica superioara (VCS)
VCI<M<VCS
Se considera ca sirul de date
experimentale are un caracter aleator (nu este afectat de erori sistematice) cu
probabilitatea 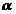 de a se verifica aceasta inegalitate. In tabele se dau
valori pentru
de a se verifica aceasta inegalitate. In tabele se dau
valori pentru 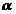 corespunzatoare
diferitelor valori ale lui n
corespunzatoare
diferitelor valori ale lui n 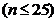
Daca n>25, 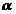 se determina cu relatia
se determina cu relatia
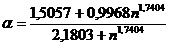
Valorile VCI si VCS pot fi luate din tabele
sau calculate cu relatiile:

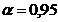
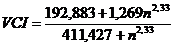
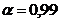
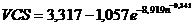
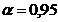
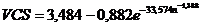
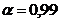
P3. Verificarea normalitatii unei
multimi (serii) de date.
Formulam ipoteza ca datele din
masuratori urmaresc repartitia Gaussiana. Putem
aproxima aceste date folosind
histograma
cu
diferenta dintre media teoretica a esantionului si mediana
acestuia
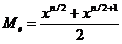 n par (este
n par (este
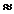 nula)
nula)
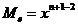 n impar
n impar
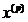 - reprezinta
valoarea de pe pozitia p din ciclul de date ordonat crescator
- reprezinta
valoarea de pe pozitia p din ciclul de date ordonat crescator
utilizand
diferenta dintre media teoretica a esantionului si modul (valoarea
cea mai probabila din esantion) 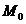 (
(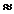 nula)
nula)
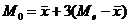
coeficientul
de boltire sa fie 3
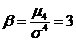
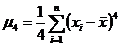
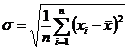
Daca aceste criterii nu sunt suficiente,
pentru verificarea normalitatii datelor din esantionul respectiv
putem folosi testele Massy sau 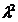 .
.
Testul Massay
 P1. Calculeaza
P1. Calculeaza 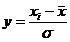 , i=1, n
, i=1, n
 P2. Calculeaza
P2. Calculeaza 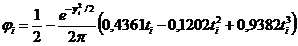 , i=1, n
, i=1, n

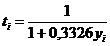 , i=1, n
, i=1, n
P3. Se calculeaza
frecventele relative cumulate
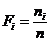 (functie de
repartitie empirica)
(functie de
repartitie empirica)  nr. de valori
nr. de valori 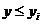
 P4. Se determina valoarea
P4. Se determina valoarea 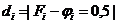 , i=1, n
, i=1, n
Se alege 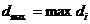
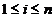
P5. Se compara 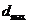 cu
cu 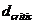 si se
considera ca esantionul are repart normala (cu medii
si se
considera ca esantionul are repart normala (cu medii 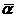 si
si 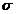 ) daca
) daca 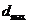 <
< 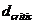
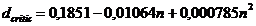
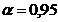
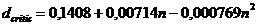
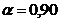
Testul 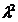
P1. Se considera sirul 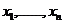 , se
ordoneaza crescator si se imparte in k clase; k=1+3,322ln n,
, se
ordoneaza crescator si se imparte in k clase; k=1+3,322ln n, 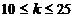
P2. Se comaseaza clasele extreme daca este cazul astfel incat fiecare clasa
sa aiba macar cinci valori.
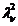 - nr de grade de libertate
- nr de grade de libertate
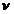 nr claselor -1
nr claselor -1
P3. Se calculeaza pentru fiecare clasa
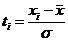 ,
, 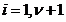
 limita superioara a clasei i
limita superioara a clasei i
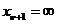
P4. Se calculeaza 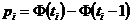 ,
, 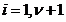
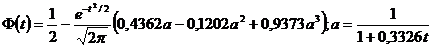
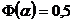
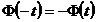
P5. Se calculeaza 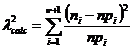
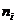 nr. de valori
nr. de valori 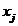 din clasa i
din clasa i
P6. Se compara 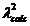 cu
cu 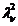 si se considera ca repart este
normala daca
si se considera ca repart este
normala daca 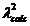 <
<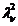
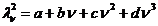 unde:
unde:
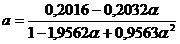 ;
; 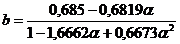 ;
;
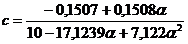 ;
; 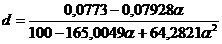
Tema: Scrieti cate un program in C++ pentru
fiecare test
MODELARE SI SIMULARE
III
Generari de variabile aleatoare
Variabile aleatoare uniforme
 Def Variabila aleatoare v este uniform repartizata pe [a,b] (sau uniform rectangulara) daca are densitatea de repartitie
Def Variabila aleatoare v este uniform repartizata pe [a,b] (sau uniform rectangulara) daca are densitatea de repartitie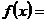
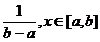
0 , 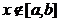
Functia de repartitie 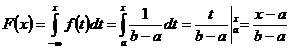
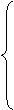 0, x<a
0, x<a
F(x)= 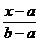
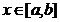
1, x>b
Propozitie Fie u ~>U(0,1)
(variabila aleatoare u este uniform repartizata pe
(0,1)). Atunci V=a+(b-a)u ~>U([a,b]) sau U(a,b)
Consecinta Prin transformarea liniara a unei
variabile uniforme obtinem tot o variabila uniforma.
Variabila aleatoare uniforma discreta
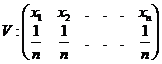
Obs 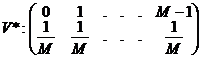
Propozitie Daca V este uniforma (repart) pe (a,b)
si 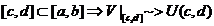
 Caz multidimensional Daca
Caz multidimensional Daca 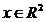 este uniform
repartizata pe [a,b]x[c,d] atunci densitatea de probabilitate o sa
fie I
este uniform
repartizata pe [a,b]x[c,d] atunci densitatea de probabilitate o sa
fie I
 f(x)=
f(x)= 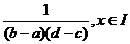
0, 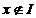
Repartitiile marginale
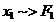
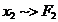
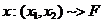
Obs. 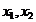 indep. statistic
atunci
indep. statistic
atunci 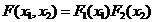
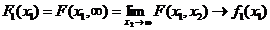 (dens marginala)
(dens marginala)
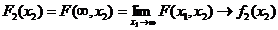 (dens marginala)
(dens marginala)
Functia de repart pentru vect
unif
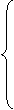 0 ,
0 ,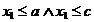
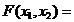
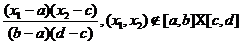
,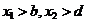
Urmatoarele doua leme
demonstreaza importanta variabilelor aleatoare uniforme.
Lema Smirnov-Hinein
Fie x variabila aleatoare
oarecare, avand functia de repartitie F(x) inversabila 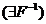 iar u
iar u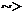 U(0,1)
U(0,1)
Atunci 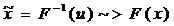
Dem 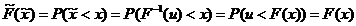 q.e.d.
q.e.d.
Varianta Smirnov 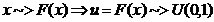
 Dem
Dem 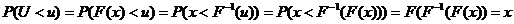 q.e.d. x
q.e.d. x
Lema 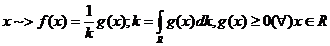
si 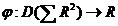 definit prin
definit prin 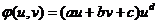 , unde
a,b,c,d
, unde
a,b,c,d 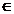 R; d#1; b#a
R; d#1; b#a
(u,v)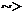 U(D), unde D este domeniul marginit dat de relatia
U(D), unde D este domeniul marginit dat de relatia 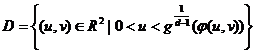
Atunci 1. 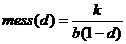

2. 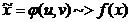 , unde f(x)definita mai sus
, unde f(x)definita mai sus
Dem. (u,v) 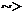 U(D)
U(D)
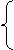 H(u,v)=
H(u,v)= 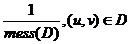
,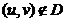
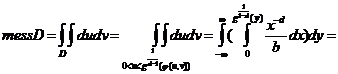
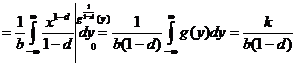
u=x
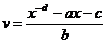
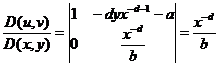
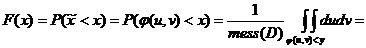
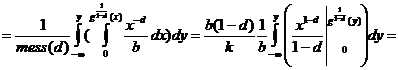

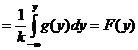 q.e.d.
q.e.d.
Procedee de obtinere de numere uniforme
Tabele
cu numere intamplatoaredau numere aleatoare pe un interval dat putand
proveni de la recensaminte.
Procedee
fizice (ex zgomotul electronic sau radioactiv receptat din cosmos)
Procedee
aritmetice = generatoare permit prin relatii de recurenta pseudo
sau cvasi nr. aleatoare
Cerinte
ce trebuie verificate de un generator
sa
fie simplu si rapid
sa
produca siruri de numere oricat de lungi si fara
repetitii (perioada sa fie foarte mare)
nr.
de produse sa fie independente statistic dar dependenta sa fie
foarte slaba
nr.
generate sa fie cat mai aproape de repartitia uniforma
Exemple
A.
Metoda
mijlocului patratului (middle squar method)
John von Neumann

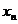 - k cifre
- k cifre
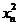 - se iau 2k cifre din
int
- se iau 2k cifre din
int
D.E.Knuth
B.
Metode
congruentiale liniare
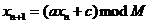 ;
; 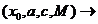 notatia
unui generator congr
notatia
unui generator congr
C.
Metoda
de amestecare a lui Marsaglia
Fie 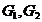 doi generatori de
numere uniforme
doi generatori de
numere uniforme
Obtinem un al treilea generator prin amestecarea
celor doua astfel: se da o lista 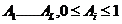 produse cu
produse cu 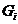 ; generam un indice aleator i cu
; generam un indice aleator i cu 
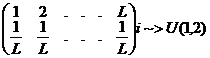 ; se considera
cu
; se considera
cu 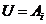
Ex L=
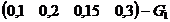
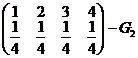
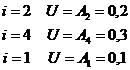
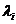 este perechea lui
este perechea lui 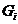 daca
daca 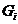 indep atunci
indep atunci 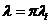
Generari de variabile aleatoare
neuniforme
Metode generale
Metoda inversa - are la baza lema Smirnov- Hincin
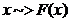 ; F
inversabila
; F
inversabila 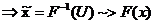
Algoritmul Inv
P0. Initializarea algoritmului pentru gen.
unif. pe (0,1) si a algoritmului calc lui 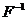
P1. genereaza 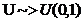
P3. Calculeaza 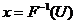
STOP!
Ex variabila aleatoare exponentiala
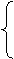
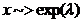 daca
daca 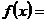
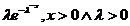
0 , 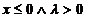
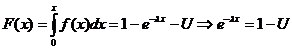
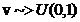
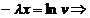
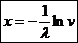
Obs Daca 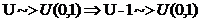
Algoritmul
exponential
P0. Intrare 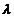
P1. Generare 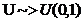
P2. 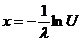
STOP!
MODELARE SI SIMULARE
V
Generarea variabilelor aleatoare de tip
GUMBEL cu metoda inversa
In statistica extremelor intervin variabile
aleatoare ale caror functii de repartitie sunt:
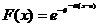 pentru maxime;
pentru maxime; 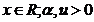
variabila aleatoare de tip Gumbel (dublu
exponentiala)
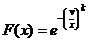 pentru maxime;
pentru maxime; 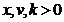
variabila aleatoare de tip Frechet 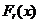
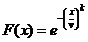 pentru minime;
pentru minime; 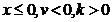
variabila aleatoare de tip
Weibvll 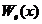
Cu schimbarea de variabila 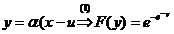 dublu
exponentiala.
dublu
exponentiala.
Pt. (1) : 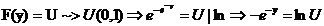
sau 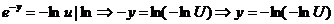
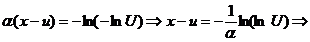
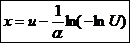 variabila
aleatoare de tip Gumbel
variabila
aleatoare de tip Gumbel
Algoritm
P0. Intrarea 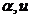
P1.
Genereaza 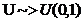
P2.
Retine 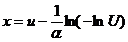
Pt. (2) Cu
schimbarea de varabila 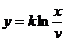 in (2)
in (2) 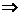 dublu exponentiala
dublu exponentiala
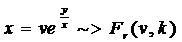
Pt. (3) cu schimbarea de variabila
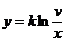
(5') 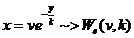
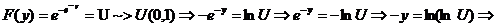
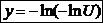
 dublu
exponential
dublu
exponential
Metoda amestecarii (Mixture method)
Aceasta metoda se foloseste pentru
variabile aleatoare de forma:
a) caz
discret 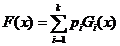
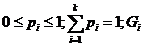 sunt functii de
repartitie
sunt functii de
repartitie
b) caz
continuu F(x)
Daca 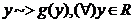 si
si 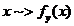 atunci dem. de rep a lui x este
atunci dem. de rep a lui x este
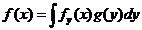
In termeni de fc de repartitie
Fie 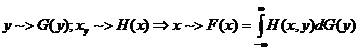
Algoritmul de compunere discreta:
P0. Intrare 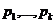
Initializarea alg:RND: care gen. v.a. cu rep 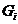
Pt. i=1,k
calculam 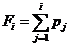
P1. repeta
j=0;
genereaza 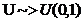
repeta
j=j+1
pana cand <U
Genereaza 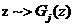
x=z
pana cand cond oprire
P2.
STOP!
Problema La o statie de benzina se prezinta
n tipuri de autpturisme pentru aprovizionare, iar 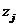 este intervalul de timp dintre doua sosiri consecutive
de automobile de tip j. Aceste variabile aleatoare sunt considerate aa au
repart
este intervalul de timp dintre doua sosiri consecutive
de automobile de tip j. Aceste variabile aleatoare sunt considerate aa au
repart 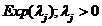 . Persupunem ca
. Persupunem ca 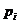 este probabilitatea ca la un moment dat sa soseasca
un automobil de tip j probabilitate cunoscuta. Fie x
variabila aleatoare ce da timpul. Dintre doua sosiri consecutive
de automobile in statie. Atunci x are fc de rep. rez. din amestecarea fc
de rep
este probabilitatea ca la un moment dat sa soseasca
un automobil de tip j probabilitate cunoscuta. Fie x
variabila aleatoare ce da timpul. Dintre doua sosiri consecutive
de automobile in statie. Atunci x are fc de rep. rez. din amestecarea fc
de rep
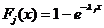 dupa vect de
probab p
dupa vect de
probab p
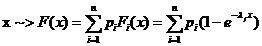
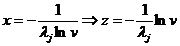
Generarea
variabilelor aleatoare cu metoda amestecarii
Algoritm
P0.
Initializarea alg RND si pentru generarea v.a. 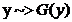
P1. Repeta
gen 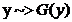
gen 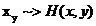

pana cand
cond oprire
P2. STOP!
Generarea variabilelor aleatoare PEARSON
de tip XI
Variabila aleatoare de tip Pearson
este un amestec de expon dupa expon

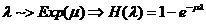
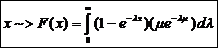 Pearson de tip XI
Pearson de tip XI
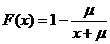
Algoritm
P0. Initializare PND; intrare 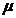
P1. repeta
Gen 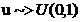
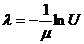
Gen 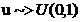
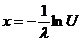
pana cand cond oprire
P2. STOP!
Metode
generale
metoda
inversa
metoda
compunerii (amestecarii)
metoda
respingerii
Sistem de respingere
Fie x o v.a. pe care dorim sa o generam.
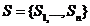 o familie de v.a. care pot fi generate cu calculatorul
o familie de v.a. care pot fi generate cu calculatorul
N v.a. care ia valori in N
P proprietate ce poate fi verificata cu calculatorul
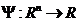 functie
masurabila pentru
functie
masurabila pentru 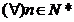 astfel incat fiind date
astfel incat fiind date  din S care satisfac proprietatea P
din S care satisfac proprietatea P 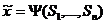 are aceeasi functie de
repartitie cu x (initial).
are aceeasi functie de
repartitie cu x (initial).
Sistemul 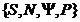 formeaza un procedeu de respingere pentru
v.a. x.
formeaza un procedeu de respingere pentru
v.a. x.
Algoritm general de respingere datorat lui
John von Neumann
P0. Initializarea alg RND pentru generarea
v.a. 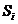 si pentru verificarea proprietatii P si calc
si pentru verificarea proprietatii P si calc 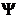 .
.
P1. Repeta
repeta
gen
n v.a. de tip N
pentru i 1,n gen 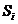
pana
cand 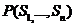
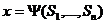
pana cand cond oprire
P2. STOP!
Lema infaturatoarei este cea care da
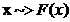 si
si 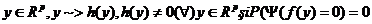
Presupunem ca 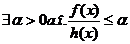 pentru
pentru 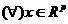 , y poate fi generat cu calculatorul.
, y poate fi generat cu calculatorul.
Atunci daca 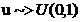 si
independent de y dens de repart a lui
y conditionata de
si
independent de y dens de repart a lui
y conditionata de 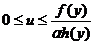 este f(x)
adica y este o realizare a lui x.
este f(x)
adica y este o realizare a lui x.
Procedeul de respingere dat de lema
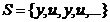
N=2
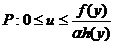
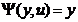
Algoritmul dat de lema
infasuratoarei
P0. Initializarea alg. RND,y; intrare 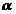
P1. Repeta
Repeta
Gen.
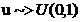
Gen.
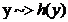
Pana
cand 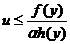 ; x=y
; x=y
Pana cand cond oprire
P2. STOP!
Se poate arata pentru acest algoritm ca
proprietatea de respingere a ciclului intern este 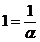
Aplicatie: gen v.a. 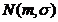
Propozitie: 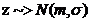 si
si 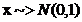 atunci
atunci 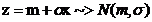
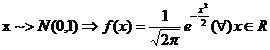
Datorita
simetriei fata de 0: 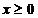 ,
, 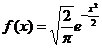
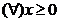
Aplicam
Lema infasuratoarei
|
x
|
|
|
|
|
r'
|
|
|
|
|
r
|
|
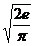
|
|
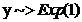 ;
; 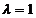 (exp. standard)
(exp. standard)
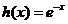
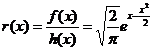
Am determinat 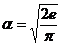
P0. Intrare 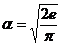 ; init RND
; init RND
P1. Repeta
repeta
Gen.
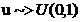
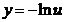
Gen. 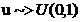
pana
cand 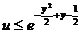
x=y
cond
oprire
P2. STOP!
Tema: Pentru lucrarea a II-a de programat alg folosind
ca exemple pentru generarea de v.a. continue si discrete.
MODELARE SI SIMULARE
VI
Generare v.a. normale si inrudite
Generare v.a. normala prin metoda polara
Teorema Box si Muller
Daca 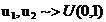 independente atunci
independente atunci 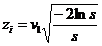 , unde
, unde
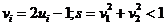 (obs.
(obs.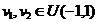 )
)
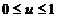
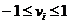
1
1
-1
Sunt v.a. N(0,1) (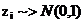 independente)
independente)
POLARA
P0. Initializare RND n nr. de realizari
P1. 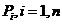 executa
executa
Genereaza
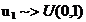
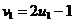 ;
;
Genereaza
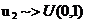
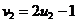 ;
;
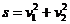
cat timp s<1
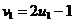 ;
;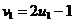
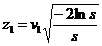 ;
;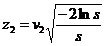
Genereaza 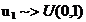
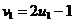 ;
;
Genereaza
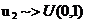
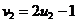 ;
;
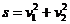
P2. STOP!
Generarea
v.a. 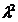
Def 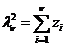 , cu
, cu 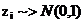 independente
independente
Densitatea de probabilitate 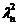
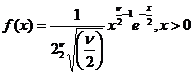
Obs 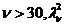 aproximeaza
aproximeaza 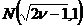
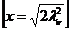
Metoda de generare HIP
Conform
definitiei generam 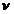 v.a.
v.a. 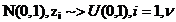
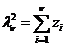
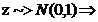
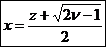
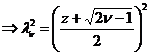 pentru
pentru 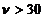
Generare v.a. t (de tip STUDENT)
Def v.a.
Student cu ν grade
de libertate este definita de relatia:
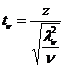 , unde
, unde 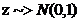 si
si 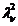 sunt independente
sunt independente
P0. Initializare RND ν si n=nr. de realizari ν
P1. i=1,n
Generam 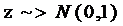
Generam
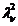 cu HIP
cu HIP
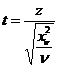
P2. STOP!
Generarea
v.a. 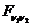 (SNEDECOR-FISHER)
cu
(SNEDECOR-FISHER)
cu 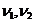 grade de libertate
grade de libertate
Def 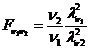
Densitatea de probabilitate: 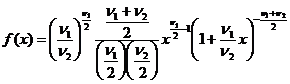
FISHER
P0. Initializare RND ; intrare 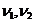 ,n=nr. de realizari
,n=nr. de realizari
P1. pentru i=1,n executa
Genereaza
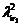 cu HIP
cu HIP
Genereaza
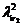 cu HIP
cu HIP
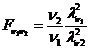
P2. STOP!
Generare v.a. lognormala
V.a. x
este lognormala daca 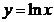 este v.a. normala
este v.a. normala
Dens. de repartitie este 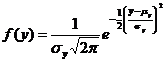 , unde
, unde 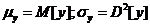 varianta lui .
varianta lui .
Pentru x:
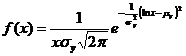 cu
cu 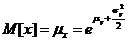 ,
, 
Legatura intre 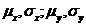
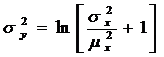 ;
; 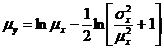
LOGNORM
P0. Initializare RND ; intrare 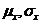 ,n=nr. de realizari
,n=nr. de realizari
Calculeaza 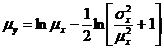
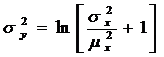
P1. pentru i=1,n
Gen 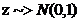
Calculeaza
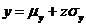
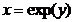
P2. STOP!

LUCRAREA A II-A
Metode de generare

 Inversa exp
Inversa exp
Gumbel

 Compunerii
discreta
Compunerii
discreta
Continua - PEARSON XI

 Respingerii lema
Respingerii lema
Metoda infasuratoarei -
normala
Metode particulare Metoda Box-Műller
Generare v.a. inrudite
Student
Fisher
Geometrica
Poisson
Generarea (unor)
v.a. discrete
variabila geometrica
Proba Bernoulli - este o experienta in care
sunt posibile numai doua rezultate

 Success
Success 
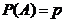
esec 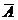
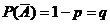 ,unde p,qє[0,1
,unde p,qє[0,1
x= v.a. care reprezinta nr. de esecuri inregistrate pana la
primul succes
atunci x este v.a geometrica
Ex: Daca v.a. poate caracteriza nr. de piese
corespunzatoare gasite in urma controlului unei multimi de piese
pana la aparitia primului rebut.
Functia de frecventa
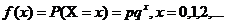 (nr. de esecuri)
(nr. de esecuri)
Functia de repartitie
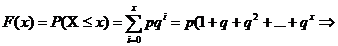
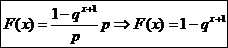 , 0≤F(x)≤1
, 0≤F(x)≤1
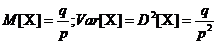
Generare v.a. geometrica
metoda
inversa
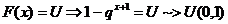
υ=1-U si 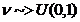
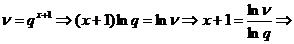
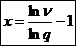
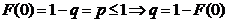
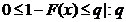
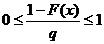
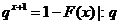
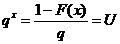
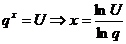 o realizare a lui x
v.a. geometrica
o realizare a lui x
v.a. geometrica
Algoritm
P0. Initializare RND ; intrare q;n=nr. de realizari
P1. pentru i=1,n
Gen 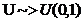
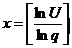
P2. STOP!
Generarea v.a. POISSON
Functia
de frecventa 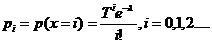
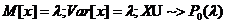
v.a. Poisson λ reprezinta nr. de
evenimente rare (intrarile intr-un sistem de asteptare/unit de timp).
Intervalul de timp dintre doua sosiri consecutive este o v.a. expon de
λ.
τ= intervalul de timp Exp(λ) astfel incat sa acopere intervalul
de timp=unitatea
Nr. j de
astfel de intervale este o selectie de a v.a. Poisson
j satisface inegalitatea dubla 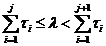 astfel il gasim
pe j
astfel il gasim
pe j
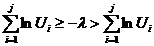 sau
sau
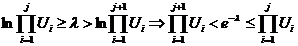
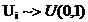
Poisson
P0. Initializare RND ; intrare n
P1. pentru i=1,n executa
j=i-1;
p=1
repeta
Gen 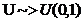
p=pU
j=j+1
pana cand 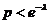
retine
x=j;
P2. STOP!
Modelare, Simulare
VII
Ajustarea
datelor
Dreapta de regresie
Fiind date intr-un sistem cartezian punctele Mi, i
= 1,6 sa se gaseasca o dreapta care trece cel mai aproape
de aceste puncte.
Rezolvare: y = ax +
b yi = axi +
b a, b necunoscute
f(x) i
= 1,6
n
S = ∑ [yi - f(xi)]2
Dc min S ) = 0 => yi
= f (xi)
i=1
min
∂S = 0
∂a a0
 => b0 => y=a0x+b0
=> b0 => y=a0x+b0
∂S = 0
∂b
Functia de regresie
Este o expresie matematica dedusa in
urma prelucrarii unor date experimentale ce aproximeaza
dependentele dintre 2 sau mai multe variabile ale unui sistem det.
Functia de regresie este necesar atunci cand dependentele dintre
variabilelerespective nu pot fi stabilite suficient de precis pe cale
teoretica.
Una dintre cele mai populare metode pentru
determinarea functiei de regresie este metoda celor mai mici patrate.
Fiind
data o multime de perechi de puncte (xi, yi) i
= T,n se pune problema determinarii unei functii y=f(x), f
numita functie de regresie, ale carei valori in punctele xi
sa aproximeze cat mai bine valoarea yi. Drept criteriu de aproximare
n
vom lua suma patratelor
corectiilor minS=min ∑
[yi - f(xi)]2
i=1
Daca determinarea expresiei f consta in
determinarea unor coeficienti atunci trebuie rezolvat sistemul
∂S = 0 cj
j=1,m coeficienti necunoscuti ai functiei f
∂Cj
Particularizare: Dreapta de regresie y=f(x),
f(x)=ax+b, c1=a, c2=b
n
min S= min ∑ (yi - axi - b)2
i=1
Determinarea punctelor stationare:
∂S -2∑
xi(yi - axi - b) = 0
∂a i=1
 => n
=> n
∂S = 0 -2∑
(yi - axi - b) = 0
∂b
i=1
n n n n n n
a ∑ xi2+b ∑xi
= ∑ x iyi ∑ xi2 ∑ xi a ∑ x iyi
i=1 i=1 i=1 i=1 i=1 i=1
=
n n n n
a ∑ xi+nb = ∑ yi ∑ xi n b ∑ yi
i=1 i=1 i=1 i=1
sistemul normal al lui Gauss
Alte forme pentru functia de regresie
1) f(x) = ax + b
2) f(x) = ax2 + bx + c
3) f(x) = a + b
x
4) f(x) = ac-x + b
5) f(x) = alogx + b
6) f(x) = a
1 + b
x
7) f(x) = 1
ac-x + b
8) f(x) = axb
9) f(x) = acb/x
10)f(x) = acbx
s.a.m.d.
Ex. numeric def. Forma functiei de regresie
6
8
5
0 4
1 9
2 7
Polinomul de interpolare al lui Lagrange
f(x):
|
x
|
x1
x2 .. x i-1 xi .. xn
|
|
y
|
y1
y2 .. y i-1 yi .. yn
|
n
L(x) = ∑yi Π x-xi
i=1 j=1 xi-xj
j≠i
Calitatea aproximarii
deviatia
standard (eroare standard) (s)
coeficientul de corelatie (r)
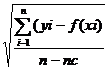 unde (xi, yi), i=
1,m, mc = numarul de coeficienti ai functiei de
regresie; ex f(x) = ax + b, nc=2
unde (xi, yi), i=
1,m, mc = numarul de coeficienti ai functiei de
regresie; ex f(x) = ax + b, nc=2
r= 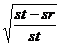 unde st
∑ (y - yi)2 y = ∑yi , Sr = ∑( yi -
f(xi) ) 2
unde st
∑ (y - yi)2 y = ∑yi , Sr = ∑( yi -
f(xi) ) 2
n
Semnificatia erorii standard este
apropiata de cea a parametrului x2 si caracterizeaza
imprastierea experim in jurul graficului functiei de regresie
si avand o valoare cat mai apropiata de zero atunci cand petele sunt
mai aproape de origine.
Valoarea acestui coeficient reprezinta o
masura mai exacta a calitatii functiei de
regresie obtinuta in situatia in care abaterea standard a
valorii experimentale este relativ mare. Functia de regresie face o
buna aproximare cu cat coeficientul de corelatie este mai apropiat de
1.
Daca datele sunt luate dintr-un fisier
text pentru separarea a doua valori se foloseste TAB-ul. Daca
fisierul contine mai multe coloane trebuie sa specificam
coloanele cu coordonatele punctelor, cele 2 coloane trebuie sa fie succesive
iar x-ul trebuie sa fie prima coloana.
Cautarea functiei de regresie optime:
putem cere efectuarea calculelor pentru toate cele 12 tipuri din program, putem
sa analizam informatia si sa retinem pe cea care
satisface cerintele. Putem defini un tip nou, fie ajustand noul existent.
Salvarea si exportarea sunt necesare pentru a
pastra, respectiv pentru a exporta datele intr-un
Odata cu salvarea si exportarea se
salveaza coeficientul de corelatie si alti
coeficienti. Putem sa vedem forma
Putem stabili forma liniei graficului si
culoarea acestuia. Le putem salva.
VIII
Metoda Monte Carlo
Proces (aleator)
Este o familie de v.a. t,
T R, T timp Dc T =
procesul se numeste lant
Dc T = I interval al lui R atunci procesul este cu timp continuu. Valorile
var Xt se numesc stari ale procesului. S este multimes starilor.
Daca S este discreta
rezulta proces cu stari discrete. Altfel, proces cu stari
continue.
Traiectoria procesului este t T
Un proces este cunoscut daca
pentru orice n ≥ 0, t1< t2 < < tn
Ft1tn(x1
. xn) - P(xt1 < x1, . xtn < xn)
Proces tare stationar daca pentru si t1 <
t2 < tn avem
Ft1+htn+h (x1xn)
= Ft1+htn (x1xn)
Proces slab stationar
(stationar) (xt)t
momente de ord 2 si sunt finite.
mt = M[xt],
Obs. 1 Pentru un proces tare stationar Ft+h
(x) = Ft(x)
Xt
pot sa nu fie independente
2
Procesul tare stationar care are momente de ord 2 este si slab
stationar; invers nu este adevarat
In simularea unui proces suntem
interesati sa producem cu calculatorul puncte ale unei traiectorii
finita.
Pb simularii unui proces revine la:
a) se da o valoare x0 pp la mom to
= 0 aflata pe traiectoria procesului
b) se cere generarea x1 pe traiectorie
pp ca valoarea to = 1
Legea numerelor mari
Fie X1, X1 Xn
. si de v.a. independente 2 cate 2 cu dispersiile marginite de
aceeasi constanta, Var[Xn]≤ C
At. Lim P( x1+.xn - M[X1]+ . .+ M[Xn ≤
) = 1 sau
n n
P( x1+.xn - M[X1]+ . .+ M[Xn]
≤
) ≥ 1 - c
n n n
Generalitati
Metode Mc = tehnici de rezolvare a diferitelor probleme utilizand numere aleatoare,
var. Aleatoare sau procese
Def. Fie de rez. O pb. Numerica P care are
solutia Ө. O metoda Mc pentru rezolvarea lui P
consta in urmatoarele:
se
asociaza in mod adecvat un proces ξ pb astfel incat cu ajutorul
lui ξ sa il estimam pe Ө.
De exemplu: Ө = M[δ δ
fiind o functie cunoscuta (data)
Trebuie determinat δ δ ξ) estimator al lui Ө, iar δ ξ) se numeste estimator primar.
se
simuleaza o selectie ξ1. ξn
si se calculeaza δn
estimator al lui δ,
de exemplu media aritmetica, numit estimator secundar
se
aproximeaza solutia lui P cu δn
Observatie: Daca estimatorul
primar δ ξ) este nedeplasat, M[δ ξ)] = Ө, atunci estimatorul secundar satisface lg numerelor mari
δn
De cele mai multe ori estimatorul primar se alege
sa fie nedeplasat.
Sa presupunem ca = Var [δ(ξ)] < ∞. Dorim sa
aproximam Ө cu o eroare acceptata data E P ( δn - ן <
E) = p = 1 -
Din lg numerelor mari putem determina pe n astfel
incat pentru E si suficient de
mici inegalitatea sa fie satisfacuta.
Volumul n al solutiei ξ1. ξn necesar
pentru a estima pe Ө prin δn cu eroarea E data si cu riscul acceptat este dat de relatia n ≥
n0, n0 = [ ] +1
Tipuri de probleme ce se pot rezolva
cu metoda Monte Carlo
- calculul integralelor
- rezolvarea sistemelor de
ecuatii liniare
- rezolvarea sistemelor de
ecuatii integrale
- rezolvarea problemelor Dirichlet
pentru ecuatii de tip eliptic
Rezolvarea problemelor de optimizare
cu restrictii, etc
Calculul integralelor
Sa se calculeze ∫10
f(x) dx =
Daca ∫ba g(t) dt;
x= t-a => dt = (b-a) dx t-a = (b-a)x
b-a t=a+(b-a)x
∫10 g(a+(b-a)x(b-a)dx
= (b-a) ∫10 g(a+(b-a)xdx = (b-a) ∫10 f(x)
dx
Metoda Monte Carlo bruta
Daca U → U(0,1) => Ө= M [f(U)]
= ∫10 f(u)du
Alegem δ = f(U) - estimator primar nedeplasat pentru Ө.
Daca U1, Un → U(0,1) => Ө = 1 ∑ f(Ui) metoda bazata
pe aceasta relatie se
n
numeste metoda Monte Carlo bruta.
Exemplu: ∫10 e dx f(x) = e-x/2
Alg pentru calculul int. simple
P0 f(x); n = valoarea esantionului
D = 0;
P1 Pt i = 1,n exec
Gen U → U(0,1)
S = s+f(u)
P2 s=s/n
Ex. 2 Integrala dubla
∫ ∫ x2 dxdy D =
y2
I = ∫ ∫ f(x,y)dxdy mess(D)
∫ ∫ 1/mess f(x,y)dxdy = mess (D) M [f]
M[f] = 1 ∑ f(xi, yi) (xi, yi) → U (D)
n
Alg pentru calculul integralei duble cu
metoda Monte Carlo bruta
P0 mess(D); init≠ializare s=0, k=0
P1 pentru i = T, n
Gen u → u(1,2)
Gen V → v(0.5,2)
Daca (u,v) D atunci k=k+1
D=D+f(u,v)
P2 I = D * mess(D)
K
X
RETELE PETRI
Generalitati
Retelele Petri reprezinta o categorie
speciala de grafuri.
Graf. x≠0 multimea nodurilor
U=XxX; U = arce
X = n numarul nodurilor
U = m num[rul arcelor
Daca (x,y) U (x,y) ≠ (y,x) atunci graf orientat
X se numeste origine, y se numeste varf
Graful este complet daca se cunosc
Diferenta dintre un graf si o retea P consta ca
multimea nodurilor e formata din 2 submultimi distincte.
X = T U P, T ∩ P
P multimea locurilor O
P multimea tranzitiilor □
Arcele in Retelele Pietri sunt unidirectionale. Un
arc nu poate lega decat o tranzitie de un loc sau un loc de o tranzitie.
La o tranzitie sau la un loc se poate ajunge cu
mai multe arce. Dintr-o tranzitie pot pleca mai multe . Un loc si o tranzitie
pot fi legate prin cel mult un arc.
Reteaua Pietri este cunoscuta prin 3 multimi: P,
T, U (multimea arcelor)
Tj → Pi (Tj, Pi)
Tranz loc de
de intrare
iesire
Pj
→ Ti (Pj, Ti)
Loc de
tranzitie
Intrare
de iesire
Evaluare
Prin evaluare se intelege o aplicatie prin care se
atribuie fiecarui arc cate un numar natural.
Daca un arc leaga Pi → Tj) atunci evaluarea arcului o
not a(Pi, Tj) Tj → Pi : a(Tj,
Pi)
Daca a(Pi, Tj) =1 nu se mai noteaza pe graf.
Matricea de incidenta contine evaluarile arcelor
Mij
Elementele de pe linia i cd j reprezinta
valoarea arcului care leaga locul Pi de tranzitia Tj daca
tranzitia Tj este de intrare in nodul Pi; daca tranz Tj este de
iesire din Pi atunci elementul are aceeasi valoare a evaluarii
arcului dar cu semn schimbat. Daca intre Pi si Tj nu exista arc,
atunci elementul mat = 0.
Ex. (-1
-1 2)
1 0 -1
0 2 -1
Marcajul unei retele Petri
Este o aplicatie care asociaza
fiecarui loc din retea un numar intreg reprezentat in interiorul
locului prin tot atatea puncte numite jetoane. Nu orice retea Petri
trebuie sa aiba marcaje, cele care au se numesc retele Petri
marcate.
Notam cu M marcajul M(2,1,0)
marcaj initial in ex., m(P1), m(P3)
Tranzitie activabila
(executabila, senzitivabila)
Pentru un marcaj m oricare Pi loc de intrare in
tranzitia Tj marcajul lui Pi≥ a(Pi, Tj)
In exemplul anterior T1 este activabila
deoarece numarul de jetoane din P1 este mai mare decat T2.
T3 nu este activabila deoarece a(T3,P3)=1 iar
m(P3)=0
Activarea consta in modificarea marcajelor
locurilor de intrare si iesire din tranzitia respectiva.
Evolutia retelei P este def. de depl.
Jetoanelor plecand din starea initiala, jetoanele trec de la un loc
la altul prin executia tranzitiei.
Reguli de evolutie
1) o tranzitie este executabila atunci
cand fiecare loc de dinaintea ei are un numar de jetoane cel putin
egal cu ponderea arcului respectiv
2)Reteaua Petri nu poate evolua decat in
exec. Unei singure tranzitii la un moment dat.
3)executia unei tranzitii se
considera instantanee si consta din:
Se scot tot atatea jetoane din locul de dinainte
cite arata ponderea arcului si se depun atatea jetoane in locul in
care urmeaza tranzitia cat sa nu depaseasca
ponderea arcului care o leaga.
Se activeaza tranzitia T2
M0=(2,1,0) M0=(2,1,0) M0=(2,1,0)
M1v=(1,1,2) M1vv=(1,2,0) M1vvv=(4,0,0)
Tipuri de retele Petri
1. Retele Petri cu
prioritati. O
astfel de retea se utilizeaza cand se doreste o alegere intre
mai multe tranzitii validate. Trebuie prec. O relatie intre
tranzitii ce pot fi activate in ac. Timp.
2. Retele Petri neautonome . Sunt extensii ale celor definite
pana acum care permit descrierea nu numai a ceea ce se intampla cat
si cand se intampla.
3. Retele Petri sincronizate La o retea autonoma spunem
ca o tranzitie poate fi exec. Daca este validata dar nu se
stie cand va fi exec., pentru retelele Petri sincronizate fiecarei
tranzitii i se asociaza un eveniment si executia se face de
tranzitie este validata si evenimentul asociat se poate produce.
4. Retele Petri temporizate Permit descrierea unui sistem a
carui functie depinde de timp. De exemplu se poate scurge un timp intre
inceperea unei operatii si sfarsitul acesteia.
5. Retele Petri . La 4 durata asoc. Unui loc este
fixa. Exista fenomene care nu pot fi modelate cu durate constante.
6. Retele Petri continue Marcajul unui loc este un numar
real, acest model permite modelarea cu
Retele Petri temporizate
Ataseaza durata de activare pentru o
tranzitie. Activarea tranzitiei intr-o Retea Petri
temporizata se face in 3 etape:
a)tranzitia este initiata prin
extragerea numarului corespunzator de jetoane din locurile sale de intrare;
b)este activata pe o perioada de timp,
jetoanele fiind inghetate pe durata de activare;
c)tranzitia este incheiata prin plasarea
de jetoane in locurile de iesire ale tranzitiei
Tranzitii=operatii; locuri=timpi de
sejur.
La activ. T2 un jeton este mutat din P1 in lucru
la momentul t=0, jetonul este inghetat in T2 3 unitati de timp,
dupa care trece in locul 3.
O tranzitie activabila nu poate fi
activata decat daca este inactiva. Pentru a fi cunoscuta pe
deplin starea unei retele Petri temporizate trebuie sa stim
marcajul, starea tranzitiei active sau inactive si timpii reziduali
(ram. Pana la incheierea tranzitiei active).
IX
Retele Petri. Prezentare generala VisualSimNet
RP graf orientat cu noduri - locuri (pozitii) P
- tranzitii T
Arcele orientate leaga - o pozitie cu o
tranzitie
-o tranzitie cu o pozitie
Pe arce sunt ponderi W sau evaluari
Marcaj (Stare) atribuie un numar de jetoane
(token)
N N
(n≥0) unei pozitii ; (M (P1),., M(Pm) ) m-numar pozitii
n-numar tranzitii
RP=(P,T,F,W,M0)
P - multimea pozitiilor (locurilor)
T - multimea tranzitiilor
F - multimea arcelor (P,T) sau (T,P)
W - ponderile arcelor
M0 - marcaj initial
Observatie P∩T = Ǿ PUT ≠ Ǿ;
RP cu capacitate infinita = nu are
restrictii asupra numarului de jetoane pentru niciun loc.
Conditii-pozitii
Evenimente-tranzitii
Retele Petri cu
probabilitati si prioritati
In retelele Petri doua sau mai multe
tranzitii modeleaza evenimente dintre care unul si numai unul se
produce la un moment dat. Se considera ca probabilitatea de
aparitie ale acestui eveniment sunt egale (situatie de conflict);
pentru a evita o astfel de situatie se utilizeaza o retea Petri
cu prioritati.
Arcele inhibatoare?? Ext. capacitatea de modelare a
retelei Petri in sensul ca un arc inhibator conecteaza o
pozitie la o tranzactie sI are rolul de a inversa logica de
validare sI executare a tranzitiei. Tranzitia respectiva
este validata numai daca numarul de jetoane din pozitia de
intrare este mai mica decat ponderea arcului.
Programul VisualSimNet
Este destinat proceselor statistice modelate cu
retele Petri
a)definirea
unui loc
p<nume loc> <capacitate> <tip
asteptare> [x<x poz> y<y poz>]
unde: nume loc → P1,. → shing
capacitate
tip
asteptare FIFO
LIFO Random
x poz, y poz coordonate grafice
b(definirea
unui marcaj
m<culoare> <numar> [<culoare>
<numar> ]
jetoane
c(definirea
tranzitiei
t<nume> <distributie>
[<prioritate>[<probabilitate>] ]
repartitia
timpului de venire
d)definirea
unui prearc
v<nume loc> <distributie>
<culoare> [<tip arc>]
e(definirea
unui postarc
z<nume loc> <distributie>
<culoare> [<tipare>]
f)definire
cadran cu text
(text/comentarii/eticheta)
C<linii>[<marime caractere>[<tip
chenar>[grosime linie>]]] [x<x poz> y<y poz]
g)definirea
distributiei timpului de servire
distributie veche/ distributie noua/ distributie
timp de servire
tip p1 p2 tip(p1[p2]) tip p1, p2, p3, p4
h)definirea
perioadei de timp
s<perioada de timp>
Comentariu → orice linie care nu incepe cu
una din literele rezervate sau cu cifrele de la 0 la 9
Separatori → spatiu, (),
Ex. p loc1 20 f
m 1 3
p loc2 10 f
m 1 5
t tranz1 g(5,10)
v loc1 k(1) 0 1
z loc2 k(1) 0 1
t tranz2 g(5,10)
v loc2 k(1) 0 1
z loc1 k(1) 0 1
Problema filozofilor
Th param p1
= 30 p2 = 60
Eat 5 10
Locatii random
Hungry: cap2,
FIFO, marking2
Full: capac2,
FIFO, free1, marking1
Fork: capac2,
FIFO, marking2
Seria de timp sau seria dinamica sau seria
cronologica reprezinta o secventa ordonata in timp de
observatii efectuate asupra unei variante. Faptul ca
observatiile se succed in sirul de date in ordinea aparitiei
lor, ne determina sa spunem ordonata in timp.
Cand masurarea valorilor seriei este
posibila la fiecare moment de timp spunem ca seria de timp este
continua. De exemplu: temperatura, presiunea aerului, tensiunea,
intensitatea curentului electric, etc.
Cand observatiile sunt facute asupra
variabilei la intervale egale de timp (de exemplu: secunde, minute, ore, zile,
luni, etc) seria de timp se numeste discreta.
Daca seria de timp continua este
transformata intr-una disctrta prin masurarea valorilor seriei
la intervale egale de timp, atunci seria obtinuta se numeste
serie de timp esantionata.
Seria de timp in care variabila nu poate fi
masurata continuu la fiecare moment de timp, insa este
posibila masurarea valorilor cumulate ale acestei variabile dupa
anumite intervale de timp egale se numeste serie de timp cumulata sau
serie de timp integrata (de exemplu cantitatea de precipitatii
masurata zilnic la o statie meteo).
O serie de timp este stationara
daca aceasta nu contine tendinte in valoarea medie, nu
prezinta modificari ale dispersiei datelor si paternuri
sezoniere.
Analiza vizuala a seriilor de timp
Datele se pot reprezenta grafic, pe axa
orizontala fiind timpul, iar pe axa verticala valorile masurate
ale variabilei de interes. Aceasta reprezentare permite evidentierea
unui comportament - patern - al varaibilei.
Se pot intalni urmatoarele situatii:
Datele
oscileaza in jurul valorii medii constante
Datele
prezinta o pronunsata tendinta crescatoare in
medie
Datele
prezinta un patern sezonier, suprapus peste unul orizontal
Datele
prezinta un patern sezonier, suprapus peste unul crescator in medie
Datele
prezinta un patern sezonier, suprapus peste unul crescator in medie
si amplitudinea paternului sezonier creste o data cu timpul
Metodologia Box - Jenkins trateaza seriile de
timp stationare, insa o serie de timp nestationara poate in
general sa fie transformata intr-una stationara.
Obiectivul principal al metodologiei Box - Jenkins
este de a determina o reprezentare pe cat posibil corecta a mecanismului
de generare a procesului care a produs setul de date, adica a modelului.
Metodologia de modelare Box - Jenkins
Reprezinta una dintre metodele cele mai
utilizate si precise de modelare si predictie pe termen scurt a
seriilor de timp. Metodologia consta in urmatoarele etape:
1. Etapa de identificare - se alege un model ARIMA
drept candidat pentru modelarea seriei de timp. Pentru masurarea
interdependentei statistice dintre datele observate se utilizeaza
functia de autocorelatie estimata si functia de
autocorelatie partiala estimata.
2. Etapa de estimare - se estimeaza
parametrii modelului ales in etapa I. Daca estimatorii pentru
coeficientii modelului ales in etapa I nu satisfac conditii care
sa conduca la stationaritate si inversabilitate, modelul va
fi respins.
3. Etapa de validare - diagnoza - se
verifica daca modelul ales este cel adecvat sau nu.
4. Daca nu se reia etapa I cu alegerea unui
alt model ARIMA si se continua procedura, altfel se utilizeaza
modelul in predictie, simulare, conducere, etc.
Stationaritatea si inversabilitatea unui proces liniar
Stationarea rezulta din conditia ca
seria Ψ (B) sa fie convergenta pentru B ≤ 1
Spectrul procesului.
Inlocuind in relatia care da functia de autocovarianta B cu e-i2πf se obtine
jumatate din spectrul total de putere al procesului, acesta fiind:
p(f) = 2σa2Ψ(e-i2πf)Ψ e-i2πf) = 2σa2 e-i2πf) 2 0≤f≤1
2
Inversabilitatea procesului
liniar π(B)zt=at este asigurata daca
ponderile πj asigura convergenta seriei π(B)
pentru B in interiorul si pe conturul discului de raza 1.
Un proces autoregresiv de
ordin p, notat AR(p), iar ponderile πi au fost notate cu Φi,
i = 1, ., p.
Au aplicatii practice
procesele AR(1),
zt = Φ1zt-1+at
si AR(2),
zt = Φ1zt-1+
Φ2zt-2at
proces numit proces de medie
alunecatoare de ordin q, notat MA(q). Aplicatii practice au in
general modelele MA(1)
zt = at
- Ө1at-1
si MA(2)
zt = at
- Ө1at-1 - Ө2at-2
Procesul ARMA(p,q) poate fi privit ca:
AR(p)
Φ(B)zt
= et cu proces MA(q), et = Ө(B) at si
MA(q) zt = Ө(B) bt cu proces AR(p),
Φ(B)bt = at
ARIMA(p,d,q) unde: p este
ordinul de regresie, d ordinul de diferentiere si q ordinul de medie
alunecatoare.
Un astfel de proces se
reprezinta prin
Φ(B)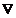 dzt =
dzt =  Ө(B)at, unde
Ө(B)at, unde 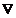 = 1-B
= 1-B
Notand wt = 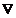 dzt
dzt Φ(B) wt = Ө(B)at, ceea ce revine la a observa
ca modelul de mai sus corespunde ipotezei ca diferentele de ordin d
ale seriei pot fi reprezentate printr-un proces ARMA inversabil,
stationar.
Φ(B) wt = Ө(B)at, ceea ce revine la a observa
ca modelul de mai sus corespunde ipotezei ca diferentele de ordin d
ale seriei pot fi reprezentate printr-un proces ARMA inversabil,
stationar.
Exprimand zt in functie de wt obtinem zt = Sd wt, unde S este operatorul de
insumare infinita, definit de relatia urmatoare:
t
Sxt= 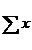 h= (1+B+B2+)xt = (1-B)-1xt
=
h= (1+B+B2+)xt = (1-B)-1xt
= 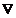 -1 xt
-1 xt
h=-∞
Relatia zt = Sd wt arata ca procesul
initial poate fi obtinut prin integrarea procesului stationar Φ(B) wt= Ө(B)at de
d ori.
De aici denumirea de proces autoregresiv integrat
si de medie alunecatoare.
Seria deviatiilor procesului original
fata de media μz constituie modelul liniar general al
seriei si are forma
∞
zt = zt
- μz = at +
Ψ1 at-1
+ at-2 +. = at + Ψt at-j
j=1
unde at , at-1 dunt variabile aleatoare
independente si identic repartizate normale de medie 0 si dispersie
σa2.
Bibliografie
- Vaduva, I., Simularea proceselor economice,
- Trandafir, R. Modele si algoritmi de
optimizare, Editura
AGIR, 2004.
- Edwards, D. , Hamson, M. Guide to Mathematical Modelling Industrial Press, Inc. New York,
2007.


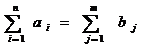 = relatie de echilibru, adica
= relatie de echilibru, adica 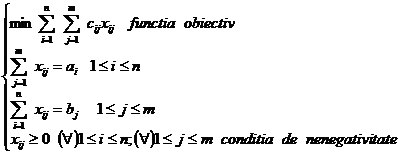

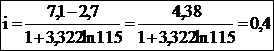
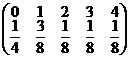
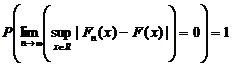
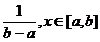
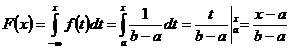
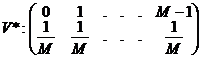
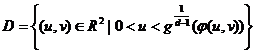
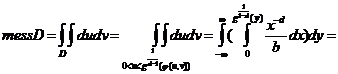
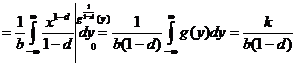
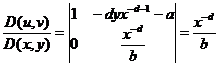
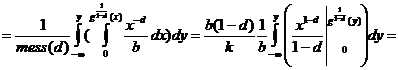
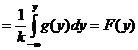 q.e.d.
q.e.d.
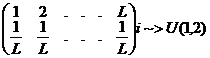
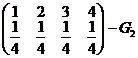
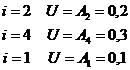
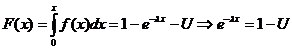
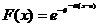 pentru maxime;
pentru maxime; 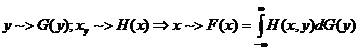
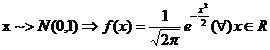
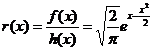

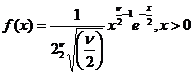
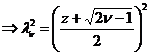 pentru
pentru 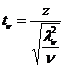 , unde
, unde 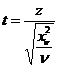
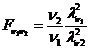
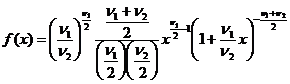
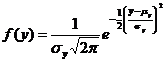 , unde
, unde 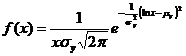 cu
cu 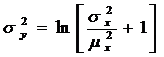 ;
;