Centrul de excelenta - clasa a vi-a

CENTRUL DE EXCELENTA - CLASA A VI-A

TEMA

A.    METODA REDUCERII LA ABSURD. EXERCITII SI PROBLEME

Metoda reducerii la absurd este o metoda specifica de demonstratie in matematica. La baza acestei metode sta una din legile fundamentale clasice legea tertului exclus ce are urmatorul enunt

Din doua propozitii contradictorii una este adevarata, cealalta falsa, iar a treia posibilitate nu exista.

Legea tertului exclus nu ne precizeaza care din cele doua propozitii este adevarata si care este falsa.

Cand la doua propozitii contradictorii aplicam legea tertului exclus este suficient sa stabilim ca una dintre ele este falsa pentru a deduce ca cealalta este adevarata.

Metoda reducerii la absurd consta in a admite in mod provizoriu, ca adevarata propozitia contradictorie propozitiei de demonstrat, apoi pe baza acestei presupuneri se deduc o serie de consetinte care duc la un rezultat absurd, deoarece ele contrazic sau ipoteza problemei date sau un adevar stabilit mai inainte. Mai departe rationam astfel daca presupunerea ar fi fost adevarata, atunci in urma rationamentelor logic corecte ar fi trebuit sa ajungem la o concluzie adevarata, deoarece am ajuns la o concluzie falsa, inseamna ca presuunerea noastra a fost falsa. Aceasta duce la concluzia ca presupunerea facuta nu este posibila si ramane ca adevarata concluzia propozitiei date.

Metoda reducerii la absurd nu se reduce la propozitia ca "a demonstra o propozitie este acelasi lucru cu a demonstra contrara reciprocei ei", deoarece pot aparea si situatii in care nu se contrazice ipoteza ci o alta propozitie (un rezultat cunoscut, o axioma, o teorema). Metoda reducerii la absurd se foloseste atat in rezolvarea problemelor de calcul de aflat) cat si la rezolvarea problemelor de "demonstrat". Metoda este des utilizata in demonstarea teoremelor reciproce, precum si in demonstrarea teoremelor de unicitate.

PROBLEME PROPUSE:

Aratati ca pentru orice fractia 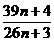este ireductibila.

Sa se arate ca nu exista numere intregi a pentru care numerele si 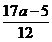sa fie simultan intregi.

Consideram trei drepte diferite a, b, c concurente intru-un punct O. Aratati ca cel putin unul din unghiurile formate are masura mai mare sau cel putin egala cu 60

Sa se arate ca daca suma a cinci numere naturale distincte (nenule) este 27, atunci printre ele se afla cel putin un numar prim.

Pe cele sase fete ale unui cub se scriu numerele de la 1 la 6 astfel incat sa nu existe fete diferite avand inscrise pe ele acelasi numar. Sa se demonstreze ca nu este posibil ca suma numerelor de pe cele trei fete care se intalnesc intr-un varf sa fie aceeasi pentru orice varf al cubului.

Demonstrati ca nu exista nici un numar natural de doua cifre care sa fie de doua ori mai mare decat rasturnatul sau.

Daca in triunghiul ABC bisectoarea unghiului B nu este si inaltime, atunci unghiul A nu este congruent cu unghiul C.

Daca in triunghiul ABC mediana corespunzatoare laturii BC] nu este si bisectoarea unghiului A, atunci latura [AB] nu este congruenta cu latura [AC].

B.    RAPOARTE SI PROPORTII

RAPOARTE

Raportul numerelor rationale a si b, b≠0, este expresia ; a si b se numesc termenii raportului.

Catul termenilor unui raport se numeste valoarea raportului.

Exemplu: valoarea raportului este 0 .

Termenii unui raport se exprima intotdeauna cu aceeasi unitate de masura.

APLICATIILE RAPOARTELOR IN PRACTICA SUNT

scara unui plan scara unei harti; probabilitatea realizarii unui eveniment procente titlul unui aliaj.

SCARA UNUI PLAN

Prin scara unui plan intelegem raportul dintre distanta din plan si distanta din realitate dintre aceleasi doua puncte, ambele distante fiind exprimate cu aceeasi unitate de masura. De obicei, numaratorul raportului prin care se exprima scara este 1.

PROBLEME PROPUSE

Care este scara planului unei gradini, daca o latura a gradinii, care are 125 m, este reprezentata in plan printr-un segment lung de 25 cm

O gradina in forma de dreptunghi, are pe un plan cu scara de dimensiunile de 4 cm si 5 cm. Ce suprafata, in hectare, are gradina in teren

Planul unui parc are scara de

a. In teren se afla un loc de forma circulara, cu raza de 1 0m, ce reprezinta lacul. Cati centimetrii are raza cercului in plan

b. Spatiul de joaca pentru copii este, in teren, un patrat cu aria de 100 m . Ce arie are in plan spatiul de joaca pentru copii

Perimetrul unui teren in forma de dreptunghi este 20 m si latimea este cu 0,2 dam mai mica decat lungimea. Sa se afle aria acestui teren in planul cu scara

SCARA UNEI HARTI

Prin scara unei harti intelegem raportul dintre distanta de pe harta si distanta din realitate dintre aceleasi doua puncte, distantele fiind masurate cu aceeasi unitate de masura, iar numaratorul raportului prin care se exprima scara este 1.

PROBLEME PROPUSE

Pe o harta cu scara de 1:500000, distanta dintre punctele A si B este de 7 cm. care este distanta in kilometri, din teren, dintre punctele A si B?

Daca la 15 cm pe o harta corespund 450 km in teren, care este scara hartii?

Aflati distanta de pe harta cu scara 1 dintre doua localitati situate in teren la 300 km una de alta.

Distanta dintre Arad si Pitesti, pe sosea, este 525 km, iar distanta pe o harta intre aceste orase este de 10,5 cm. Sa se determine scara hartii.

Distanta dintre Paris si Bucuresti este de 2550 km. Care va fi distanta in cm, dintre aceste orase pe o harta cu scara de 1

PROPORTII

Def Egalitatea a doua rapoarte se numeste proportie.

Termenii celor doua rapoarte se numesc termenii proportiei.

Orice proportie are patru termeni.

Forma generala a unei proportii este ,  unde a, b, c, d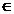Q, b≠0; d≠0.

Termenii a si d se numesc extremii proportiei.

Termenii c si b se numesc mezii proportiei.

Proprietatea fundamentala a proportiilor: in orice proportie produsul extremilor este egal cu produsul mezilor.

PROBLEME PROPUSE

Se da . Sa se afle .

Sa se afle numerele naturale x si y diferite de 0, astfel ca 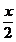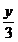si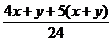

Sa se afle 3 numere, stiind ca raportul dintre primul si al doilea este 0,(6) , raportul dintre al doilea si al treilea este 0,8(3) , iar produsul dintre primul si al treilea numar este 9331,3.

Sa se afle ariile a doua dreptunghiuri, stiind ca raportul lungimilor lor este 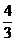, raportul latimilor lor este 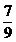, iar diferenta ariilor este 4.

Suma a doua fractii cu acelasi numarator este 1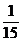. Raportul numitorilor este . Sa se afle cele doua fractii.

Numerele a si b (a>b) impartite la 5 dau acelasi rest. Stiind ca diferenta dintre ele este 520, iar raportul caturilor este egal cu 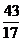, aflati multimea numerelor care satisfac aceste conditii.

Aflati masurle a doua unghiuri suplementare cu raportul egal cu .

C.    METODA TRIUNGHIURILOR CONGRUENTE

In geometrie se foloseste o metoda de stabilire a adevarului caracteristica stiintelor matematice demonstratia. Demonstratia este o succesiune de judecati, de argumente prin care se stabileste un adevar. In particular metoda triunghiurilor congruente este o metoda de demonstratie prin care se demonstreaza de regula ca doua segmente sau doua unghiuri sunt congruente.

Pentru rezolvarea problemelor de geometrie

cititi cu atentie problemele si folosind instrumentele potrivite, desenati figura geometrica.

figura desenata sa respecte proportiile elementelor date in enuntul problemei.

figura sa fie suficient de mare si clara.

pentru a demonstra ca doua segmente sau ca doua unghiuri sunt cngruente, cautati sa le incadrati in doua triunghiuri a caror congruenta poate fi demonstrata.

veti trage concluzia ca segmentele sau unghiurile respective sunt congruente, daca sunt elemente omoloage in triunghiuri congruente.

PROBLEME PROPUSE

Fie C un punct pe dreapta AB, C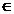(AB). Punctele M si N sunt in acelasi semiplan determinat de dreapta AB, astfel incat M este in interiorul unghiului NCB, m(<MCN)= si ∆CBM≡∆CNA.

a. Aflati masura unghiului BCM. Justificare.

b. Aratati ca [NC este bisectoarea unghiului ANM.

Fie <XOY si <YOZ doua unghiuri adiacente congruente si A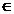(OX, M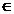(OY, B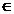(OZ, astfel incat segmentul [OA]≡[OB] si A, M, B sunt necoliniare. Fie AB∩OM . Aratati ca:

a. [AM] ≡[BM]

b. AB_┴OM

In ∆MNP stim ca A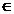(MP), B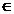(NP), [PA]≡[PB] si <PAN≡<PBM. Aratati ca

a. [NP]≡[MP]

b. <ANB≡<BMA

c. [AM] ≡[BN]

In ∆ABC, AD_┴BC, D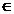(BC) si <BAD≡<CAD. Fie E si F doua puncte pe BC, C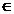(DE), B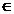(FD) si <CAE≡<BAF. Aratati ca

a.  [AB]≡[AC]

b. [AE]≡[AF]

c.  [BE]≡[CF]

Pe laturile unui unghi ascutit XOY se considera punctele A, B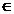(OX, C, D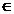(OY, astfel incat [OA]≡[OC] si [OB]≡[OD]. Sa se arate ca punctul de intersectie al segmentelor [AD] si [BC] se afla situat pe bisectoarea unghiului XOY.

In varful A al triunghiului ascutitunghic ABC se construieste AM AB, [AM]≡[AB] si AN AC, [AN]≡[AC]. Aratati ca [BN]≡[MC] in fiecare din cazurile

a.  Punctele M si B sunt in acelasi semiplan determinat de dreapta AC iar punctele N si C sunt in acelasi semiplan determinat de dreapta AB.

b. Punctele M si B sunt in semiplane diferite determinate de dreapta AC, iar punctele N si C sunt in semiplane diferite determinate de dreapta AB.