COEFICIENTI
DE CORELATIE PARAMETRICI
1.
COEFICIENTUL DE CORELATIE
BRAVAIS - PEARSON
Se utilizeaza atunci cand cele 2 variabile
prezinta distributii normale la nivelul de populatie si
sunt variabile continue.
r = 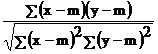 formula
de definitie
formula
de definitie
r =  formula
de calcul ax
= T, ay = T'
formula
de calcul ax
= T, ay = T'
r = 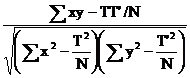
Interpretarea
valorilor obtinute se face prin raportare la tabel, in functie de
numarul gradelor de libertate.
numar grade de libertate =
N - 2
df(N) = N - 2
unde N = numarul de
subiecti
O
categorie aparte de studii vor sa stabileasca relatia care
exista intre o variabila continua si una dihotomica
(admis - respins)
T
varianta dihotomica = coeficient de corelatie biserial
T
varianta trihotomica = coeficient de corelatie triserial
PROBLEMA 1
Studiul relatiei dintre un test de atentie
si o proba aritmetica - 12 subiecti
Ta = x test de
atentie
Pa = y proba
aritmetica
N = 12 (12 subiecti)
|
x
|
y
|
xy
|
x2
|
y2
|
|
1
|
6
|
4
|
24
|
36
|
16
|
|
2
|
6
|
7
|
42
|
36
|
49
|
|
3
|
3
|
6
|
18
|
9
|
36
|
|
4
|
8
|
6
|
48
|
64
|
36
|
|
5
|
6
|
7
|
42
|
36
|
49
|
|
6
|
5
|
7
|
35
|
25
|
49
|
|
7
|
4
|
8
|
32
|
16
|
64
|
|
8
|
8
|
8
|
64
|
64
|
64
|
|
9
|
8
|
4
|
32
|
64
|
16
|
|
10
|
8
|
5
|
40
|
64
|
25
|
|
11
|
9
|
9
|
81
|
81
|
81
|
|
12
|
5
|
3
|
15
|
25
|
9
|
|
T=76 (ax)
|
T'=74 (ay)
|
axy = 473
|
a x2 =520
|
a y2 = 494
|
Histograma pentru y
|
y
|
3
|
4
|
5
|
6
|
7
|
8
|
4
|
|
I
|
II
|
I
|
II
|
III
|
II
|
I
|
|
f
|
1
|
2
|
1
|
2
|
3
|
2
|
1
|

-
val. min. = 3
-
val. max. = 9
-
intervalul (intinderea datelor)
cati
x avem: 9 - 3 +1 = 7
(1
2 3 4 5 6 7)
3 frecvente
maxime
3 4 5 6 7 8 9
Important: se intocmeste histograma atat pentru x cat si pentru
y, ca sa stim ce coeficient aplicam.
* daca distributiile sunt simetrice folosim coeficientul
Pearson
r = 
r =  = 0,11
= 0,11
N = 12
df = N-2 (nr. grad de libertate)
df = 10 - ne uitam in tabelul tipizat din
cartile de statistica
|
 df df
|
pragul 0,05
|
pragul 0,02
|
pragul 0,01
|
|
10
|
0,526
|
0,658
|
0,708
|
Pasii pentru calculul
coeficientului Pearson in programul SPSS 15.0 sunt urmatorii.


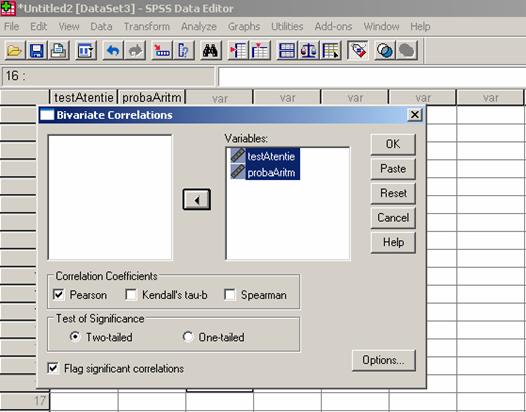
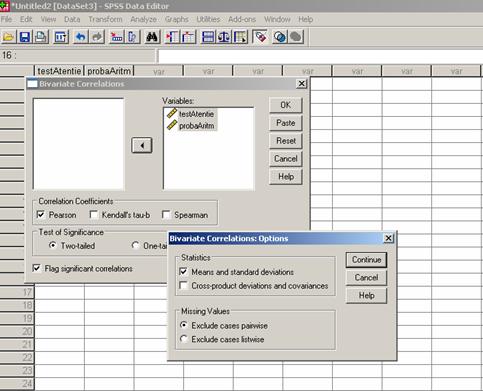
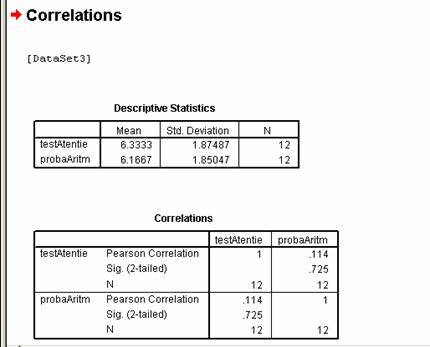
Astfel, vom obtine o analiza descriptiva a datelor
precum si rezultatele testului statistic realizat. Prin urmare coeficientul Pearson obtinut este de .114 la un p = .725 mai mare decat pragul
critic de p = .05 ceea ce ne determina sa spunem ca riscul de a
gresi este mai mare de 5% si prin urmare nu ne putem pronunta
asupra ipotezei specifice.
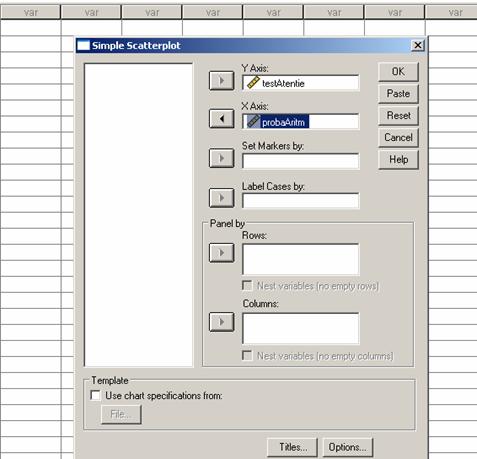
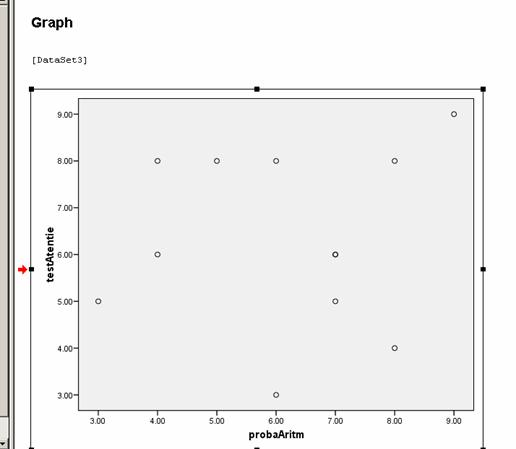
Pentru a realiza norul de puncte vom parcurge
pasii prezentati in ecranele urmatoare.

2.
COEFICIENTUL DE CORELATIE
BISERIAL:
Se utilizeaza cand avem:
o variabila continua si prezinta
distributie normala (x) proportii
o variabila dihotomica N > 50 (numarul de subiecti)
r.bis. =  , unde
, unde
p = proportia celor
admisi
q = proportia celor
respinsi /q = 1 - p/
raportul  se citeste din
tabelul f(p,q)
se citeste din
tabelul f(p,q)
m' = media admisi
m' = media respinsi
s =
abaterea standard a ansamblului de date (pe admisi + respinsi
impreuna)
Se calculeaza eroarea tip:
E = 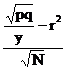
 /y - din tabel
/y - din tabel
3. COEFICIENTUL DE CORELATIE TRISERIAL:
Se utilizeaza cand avem:
o variabila continua si prezinta
distributie normala (x) - proportii
o variabila trihotomica
r.tris. =  , unde
, unde
m' , m' = mediile extreme (mijlocul nu se ia in
considerare) - ex. Test pentru cei cu rezultate bune si slabe
 raportul
raportul  se citeste
dintr-un tabel special
se citeste
dintr-un tabel special
y' y'
p' p'
4.
COEFICIENTUL DE CORELATIE
ENEAHORIC
Se utilizeaza cand ambele variabile se grupeaza
in 3 categorii (clase):
1.
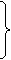 slab
slab
2.
mediu cel mai intalnit
3.
bun
Ne intereseaza doar extremele
D = n4 + n1
A = n4 + n3
B = n1 + n2
C = n3 + n2
|
|
S
|
M
|
B
|
|
|
b
|
|
n4
|
|
n1
|
D
|
|
m
|
|
|
|
|
|
|
s
|
|
n3
|
|
n2
|
C
|
|
|
A
|
|
B
|
|
r = 
r = 2g
g =
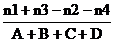


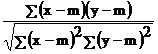

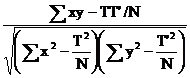










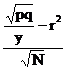
 , unde
, unde
